复合材料壳体结构损伤演化多尺度表征与强度智能预测进展

杨正伟，张 言，张赛赛，寇光杰，刘梦庆，蔡 辉，谢星宇

（1.火箭军工程大学导弹工程学院，陕西 西安 710025；2.火箭军工程大学基础部，陕西 西安 710025）

近年来，纤维增强复合材料（Fiber Reinforced Composites，FRC）因结构质量轻、可设计性强、力学性能好等无可比拟的优势，在航空航天、工业制造、医疗器械、运动设备和建筑结构等领域获得了广泛的应用［1-4］。其中，航空航天领域的结构轻量化设计应用最具代表性。波音777 客机上纤维增强复合材料的用量仅占12%，但当波音客机发展至787梦想系列时，机身蒙皮及机翼主要部分均采用了纤维增强复合材料，占比已高达50%［5］。在战斗机领域，美国F-22和我国歼-20也使用了大量纤维增强复合材料。作为人类最快的运载工具，火箭在使用纤维增强复合材料上更具优势，这一方面的主要代表是美国火箭实验室（Rocket Lab）2021 年公布的全球首枚碳纤维增强复合材料大型运载火箭“中子”（Neutron）号，该火箭计划于2024 年首飞。目前，在大型运载火箭领域纤维增强复合材料的应用主要集中在液体火箭发动机贮箱［6］和固体火箭发动机纤维缠绕壳体［7］两个方面，可减少约30%的结构质量，极大地提升火箭的运载能力。2021 年，我国首个3.35 米直径碳纤维缠绕复合材料液氧贮箱原理样机在中国运载火箭技术研究院诞生；同年，世界上最大推力的3.5米直径碳纤维缠绕复合材料整体式固体火箭发动机在航天科技集团四院试车成功。这标志着我国在航天复合材料应用领域的一大进步，对推动我国大型/重型运载火箭技术发展具有里程碑意义。

得益于纤维缠绕复合材料壳体技术的发展，固体火箭发动机壳体特征系数（Performance Factor，PF）早已从5 km—8 km提升至50 km［8］。美国在20世纪就将玻璃纤维应用于民兵系列固体战略导弹［9］；成功将Kevlar纤维增强复合材料应用于三叉戟D5导弹的III 级发动机壳体，现在又将IM7 碳纤维用于该导弹的I、II 级发动机壳体。相比之下，俄罗斯SS 系列固体战略导弹（SS-24，SS-25 和白杨-M）主要采用APMOC 纤维缠绕复合材料壳体技术［10］。目前，我国部分固体火箭发动机壳体也采用了玻璃纤维和碳纤维缠绕复合材料。

由于碳纤维的各向异性、纤维和基体本构特征区别很大、纤维—基体界面初始缺陷及层间强度理论不够完备，现有理论和数值模型在描述纤维缠绕复合材料损伤演化行为和强度预测方面仍值得开展大量研究。一方面，纤维缠绕复合材料由于结构组分的各向异性，对冲击、层间剪切等载荷十分敏感，而纤维缠绕复合材料结构破坏是一个损伤累积的过程，纤维、基体、纤维—基体界面和层间产生的损伤逐步积累，引起基体膨胀、空隙、纤维拔出、断裂，造成结构性能下降，影响其承载力和疲劳性能等，甚至引起固体火箭发动机燃烧爆轰等灾难性后果。另一方面，纤维缠绕复合材料结构在服役过程中主要承受长贮过程中的静力载荷、温度载荷、交变应力载荷和工作周期中飞行、发射、装卸、搬运、输送、维修等过程中产生的高过载、高压强、振动、冲击等，复杂的服役条件对纤维缠绕复合材料壳体结构力学性能提出了更高的性能要求。此外，由于纤维缠绕复合材料壳体的工艺比纤维增强复合材料层合板更加复杂，壳体结构中除存在固化应力外，还存在缠绕张力产生的预应力，采用层合板理论计算往往精度不高，但采用网格理论又会得到偏大的强度预测值，这给纤维增强复合材料壳体结构强度理论乃至固体火箭发动机技术的发展带来了极大的挑战。近年来，随着高精度表征测试技术的不断提升和复合材料计算力学的持续发展，在纤维本征特性尺度上基于代表性体积元（Representative Volume Element，RVE）构建纤维增强复合材料宏观—细观损伤演化行为联系的复合材料多尺度计算力学日趋成熟，使得纤维增强复合材料损伤演化和强度预测的准确表征计算成为现实。目前，复合材料多尺度计算力学主要应用在纤维增强复合材料层合板和二维/三维编织复合材料领域，在固体火箭发动机纤维缠绕复合材料壳体领域鲜有应用；而纤维缠绕复合材料壳体缠绕张力对结构强度也会产生一定影响［11］［12］，加之RVE 中存在基体真实应力问题［13］，导致目前尚未形成相应的壳体结构多尺度失效理论。然而，多尺度计算过程需要消耗大量计算资源，对计算机算力要求较高。人工智能技术的爆炸式发展使得许多机器学习（Machine Learning，ML）方法，如多层感知机（Multi-layer Perceptron，MLP）［14］［15］、自洽聚类分析（Selfconsistent Clustering Analysis，SCA）［16］、BP（Back Propagation）神经网络［17］［18］、卷积神经网络（Convolution Neural Network，CNN）［19］、深度学习（Deep Learning，DP）［20］等，被应用于界面问题、纤维增强复合材料参数预测、RVE形貌生成和结构强度计算中，大大提升了多尺度计算效率。

在纤维缠绕复合材料壳体等纤维增强复合材料中，作为增强体的纤维和作为基体的树脂模量、刚度、本构特性差异巨大，导致采用宏观力学手段得到的复合材料损伤演化失效结果存在一定误差，在航空航天领域高端装备（如飞机、火箭、导弹等）应用效果较差。随着计算机算力的发展和数值模拟技术的日趋成熟，以跨宏细观参数传递为主的复合材料多尺度表征计算应运而生，得到了世界各国学者和研究人员的关注。目前，主要集中在单向纤维增强复合材料宏观力学特性参数（主要是工程弹性常数）预测、纤维随机分布细观代表性体积元RVE 高效几何建模、纤维增强复合材料损伤演化多尺度表征与强度计算方面。此外，随着人工智能技术的发展，许多机器学习方法被应用于纤维增强复合材料参数和结构强度预测中，大大提升了计算效率，这也成了目前复合材料力学领域一个重要的研究方向。因此，本文将对上述研究领域发展现状进行综述，捋清主要发展脉络，凝练当前研究的发展瓶颈，预测未来主要发展趋势。

1 单向纤维增强复合材料宏观工程弹性常数预测

预测单向纤维增强复合材料宏观工程弹性常数是多尺度表征和材料基因工程技术［21］的核心内容，对于复合材料在不同领域的应用及其结构强度评估具有重要意义。目前，预测单向纤维增强复合材料（简称“单向板”）工程弹性常数的方法可分为试验方法［22］和计算方法［23］两种。若对不同材料及组分配比的单向板频繁使用试验方法获得其工程弹性常数，需要花费大量时间和物质资源，导致成本偏高［24］；相比之下，由于纤维和基体类别有限，在得到不同纤维和基体的工程弹性常数后，采用计算方法显得尤为方便［25］。因此，计算方法被广泛用于预测单向板工程弹性常数。

纤维增强复合材料RVE如图1所示，基于该模型和细观力学理论，计算方法发展出了解析法［25］和数值法［26］两个大类。解析法的优势是不仅能够基于纤维和基体的组分性能预测单向板工程弹性常数，而且可以便捷地利用单向板工程弹性常数反演得到纤维和基体的组分性能。这为纤维增强复合材料力学行为分析和新型复合材料设计带来了极大的应用价值。与之不同的是，数值法的主要优势体现在高精度的预测结果和与其他数值方法（如有限元分析）的强耦合能力［27-29］。然而，解析法简便但计算精度低，数值法精度高但计算复杂。截至目前，数值法仍是宏观复合材料尤其是复杂结构领域力学行为分析和强度计算的主要方法［30］。解析法因其便利性，更加适用于工程应用和制造领域。鉴于解析法和数值法的诸多特点，研究人员一直在对这两种方法进行发展［25］［31］［32］。

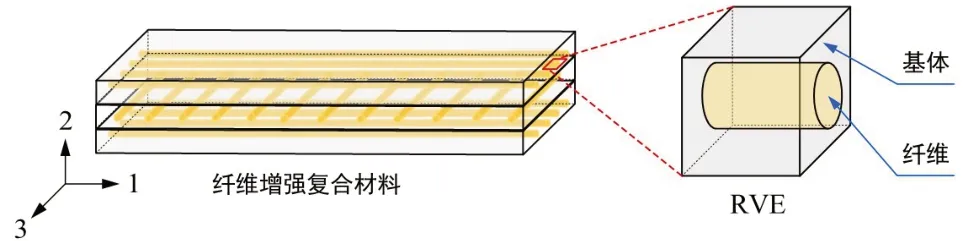
图1 纤维增强复合材料RVE

就解析法发展而言，Voigt［33］通过单向板轴向加载给出了工程弹性常数的上限，而Reuss［34］则基于横向加载确定了工程弹性常数下限。在此基础上，一个最经典的解析模型诞生了：混合（Rule of Mixture，RoM）模型［35］。RoM 模型在纤维增强复合材料多尺度力学领域得到了广泛应用，但预测精度较低。因此，对RoM 模型进行改进势在必行［36］。Halpin-Tsai（HT）模型［37］作为一种改进模型，主要优势是它作为半经验模型，增加了2个系数。Chamis模型［38］［39］是另一个著名的解析模型。在该模型中，Chamis提出了5个工程弹性常数的计算公式，其精度高于RoM 模型。通过在纤维和基体间建立桥张量，黄争鸣［40］发展了预测单向板工程弹性常数的桥联模型，且预测精度较高。2015 年，王艳超和黄争鸣基于试验数据改进了桥张量［41］。除了上述模型外，围绕夹杂理论也发展出了很多知名的模型：自洽（Self-consistent，SC）模型、广义自洽（Generalized Self-consistent，GSC）模型、Mori-Tanaka（M-T）模型等［42］。SC 模型由Hill［43］和Budiansky［44］提出，该模型认为：纤维作为夹杂，被包裹在无限大均质基体介质中。然而，该模型预测横向剪切模量时精度较低。Christensen 和Lo［45］［46］为解决上述问题，基于三相模型将SC 模型发展为了GSC 模型，其预测精度得到了提升。而后，通过改变基体的远场载荷，能够考虑纤维—基体相互作用的M-T 模型出现了［47］。单向板工程弹性常数预测结果表明，M-T模型极具优势［48］，但Eshelby张量导致模型求解十分复杂［49］。Abaimov 等［50］计算得到了解析表达式，简化了M-T 模型的计算，促进了该模型的应用。最近，Raju 等［50］和Fedotov［51］基于理论和试验方法对M-T 进行改进，提升了其预测精度。上述模型对单向板工程弹性常数预测做出了卓越的贡献，但大部分的改进模型都需要引入半经验系数进行求解，因此，鉴于解析法的优势，对这些模型进行改进或发展新的模型必不可少。

数值法主要涉及有限元（Finite Element，FE）方法和数值均匀化理论。Sun 和Vaidya 的工作［52］是数值法的代表，他们基于方形RVE 和六边形RVE，结合简单宏观应力应变均匀化理论，预测了单向板工程弹性常数。Vignoli 等［25］虽然采用了同类型的RVE，但使用渐近均匀化理论预测了工程弹性常数。在数值法中，周期性边界条件是一个重要概念，Li 等［53］对RVE 施加周期性边界条件进行了细致阐述。然而，对于实际的纤维增强复合材料而言，纤维沿单向板截面的分布是随机的，这会给单向板工程弹性常数预测结果带来误差。于是，出现了两种用于实现纤维随机分布RVE 的方法［54］［55］。基于此，Koley 等预测了同一纤维体积分数（Fiber Volume Fraction，Vf）但不同纤维随机分布RVE 的单向板工程弹性常数。结果表明，随着纤维体积分数的增加，纤维分布对预测结果造成的误差影响逐渐减弱［56］。除纤维随机分布外，纤维截面有时也不是标准圆形［57］。考虑这种真实情况，Higuchi等［58］使用不同纤维截面类型的RVE，研究了不同纤维截面对单向板工程弹性常数预测结果的影响。他们发现，当纤维随机分布时，纤维截面形状预测结果对预测结果的影响不大。值得注意的是，纤维和基体间的界面问题是数值法研究的重点。Xin 等［59］通过建立包含纤维、基体和纤维—基体界面的RVE，预测了单向板工程弹性常数。而后，Chen等［15］使用机器学习中的人工神经网络（Arti fi cial Neural Network，ANN）预测了单向板工程弹性常数。目前，数值法也被拓展到了多轴编织复合材料的宏观工程弹性常数预测与多尺度表征上［29］［60］。然而，建立可靠的RVE 往往需要进行有限元软件前处理二次开发或重复进行几何建模，因而采用数值法对于新型复合材料的设计与分析多有不便。

对比解析法和数值法的发展可以发现，即使解析法的精度偏低，但也因其便利性和反演能力在纤维增强复合材料力学性能多尺度预测领域更具优势。数值法虽然在工程弹性常数预测上表现并不突出，但因其精度高、可视化及强大的有限元耦合能力，在纤维增强复合材料损伤演化多尺度表征模拟领域应用广泛。

2 纤维增强复合材料纤维随机分布RVE 高效建模

前述提到，数值法与有限元分析的强耦合能力决定了其在纤维增强复合材料多尺度表征模拟计算中的牢固地位。因此，有限元方法成了复合材料领域的一种通用研究方法。随着计算机算力的发展和高精度表征测试技术的进步，有限元方法成为复合材料领域最具前景的计算方法之一［61］［62］。但要采用有限元方法对纤维增强复合材料损伤演化行为进行多尺度表征，第一步就是在细观尺度上建立起能够表征对象结构细观形貌的RVE。图2 展示了经典的RVE 几何结构：不含界面的RVE（由单根纤维+基体组成）和含界面的RVE（由单根纤维+基体+界面组成）。在这种经典RVE 中，纤维分布被认为是均匀分布、一致排列的［26］［32］。然而，大量研究表明，纤维分布是随机化的［58］［63-65］。图3所示的SYT55S碳纤维增强复合材料细观形貌很好地展示了这种随机分布现象。

图2 经典的RVE几何结构

图3 SYT55S碳纤维增强复合材料细观形貌

为建立纤维增强复合材料真实情况下的纤维随机分布RVE，研究人员们提出了许多行之有效的方法。作为较早研究该问题的团队，Buryachenko 等［66］阐述了纤维随机分布的背景，并对其进行了定义；而后，基于数字图像处理过程提出了获得纤维中心点坐标的纤维随机分布RVE 方法。类似地，Hojo 等［63］基于HTA/RTM6单向板横截面的扫描电镜原始图像，提出了实现纤维随机分布RVE 的数字图像方法。Wang等［67］则总结了基于扫描电镜图像的纤维随机分布RVE 数字图像建模的一般机制。然而，几何模拟方法成本低廉，相比于数字图像建模，显然优势更大。Oh等［68］提出了一种纤维随机分布RVE的直接随机化生成算法，但并未对高纤维体积分数的RVE 和周期性边界条件展开研究。鉴于此，Melro 等［69］提出了一种用于生成纤维随机分布RVE 的快速简便算法，以此解决高纤维体积分数的纤维随机分布RVE生成问题。在此基础上，Vaughan 和McCarthy［64］根据几何建模中新纤维的方向角和中心坐标，发展了最近邻算法（Nearest Neighbor Algorithm，NNA）用于生成纤维随机分布RVE。根据中心核模型，Yang 等［54］提出了随机序列扩展（Random Sequential Expansion，RSE）算法生成纤维增强复合材料中的高纤维体积分数纤维随机分布RVE，并基于该RVE 预测了单向板工程弹性常数。生成纤维随机分布RVE 不仅可以通过增加纤维的算法实现，也可以采用减少纤维的算法实现。Park 等在这一方面开展了原创性工作［55］。首先，基于RSE 算法建立了纤维体积分数为65%的主模型RVE；而后，通过从主模型RVE 中随机去除纤维，实现了不同纤维体积分数的纤维随机分布RVE生成。

生成高纤维体积分数的随机纤维分布RVE 成了目前的发展趋势。Ge 等［70］介绍了一种用于改变纤维初始随机化后不合理位置的有效迭代调整机制，进而生成了纤维体积分数高达70%的纤维随机分布RVE。Liu 等［71］提出了一种快速化建模算法，基于该算法所生成的纤维随机分布RVE 的最高纤维体积分数可达到80%。不同于其他算法调整纤维间两两距离的措施，Wang 等［72］另辟蹊径，结合德劳内三角形特征发展了一种新的纤维随机分布RVE 生成算法，解决了传统RVE 生成算法出现的纤维随机分布区域不合理的问题。然而，上节已经说明，在实际纤维增强复合材料中，纤维截面有时也不是标准圆形。因此，Herráez 等［73］［74］通过建立三叶草形、四叶草形、圆角方形、椭圆形和C 字形几何方程，基于迭代机制提出了一种可有效实现高纤维体积分数的非圆形纤维随机分布RVE 生成算法。

上述研究为纤维随机分布RVE 生成奠定了算法基础，极大地推动了纤维增强复合材料细观力学数值模拟及多尺度表征方法的发展。然而，对于现有大多数算法（如NNA、RSE 等），在RVE 生成过程中必须判断每一对纤维间距离是否满足算法设定的纤维间最小距离要求，容易造成计算资源浪费，并在无形中提升了算法的时间复杂度。此外，实际生产中，纤维增强复合材料细观尺度上存在纤维截面形状各异、孔隙多元化和纤维局部聚集/稀疏的情况。因此，通过发展新的算法解决这些问题，是未来必须发展的研究方向。

3 纤维增强复合材料损伤演化多尺度表征与强度预测

宏观上表现为各向同性的材料在细观和微观尺度可能表现为各向异性。纤维增强复合材料由于组分区别，即使是单向板也表现为横观各向异性，而碳纤维增强相关的研究目前已拓展到纳米尺度，如何通过微观和细观尺度上的组分本征性能预测复合材料宏观性能，是经典层合板理论和连续介质力学难以解决的问题［42］。另一方面，宏观结构在服役环境中遭受载荷时，其结构破坏往往由经典复合材料失效理论（如Hashin 准则、Tsai-Wu 准则、Tsai-Hill 准则、Puck 准则等）进行分析，但在宏观表现未出现损伤时其组分（如基体、纤维—基体界面）有可能已经出现损伤。这对研究一些结构如碳纤维增强复合材料无内衬V 型压力容器的安全性非常重要。因此，鉴于多尺度表征计算方法能够在复合材料力学领域建立细观特性与宏观表现联系的巨大优势，其在复合材料领域已经成为力学性能评估的主要手段之一［75］-［77］。以跨宏细观参数传递为主的复合材料多尺度表征计算方法主要可分为三种［78］：（1）单向多尺度分析［79］：细观和宏观间仅存在单向数据流，是一种层次分明的顺序多尺度方法，一般用在细观→宏观参数预测领域。（2）协同多尺度分析［80］：细观和宏观间存在双向数据流，是一种半并发的多尺度方法，在单向多尺度分析的基础上还可用于宏观→细观组分损伤研究。（3）并发多尺度分析［16］：细观和宏观间仅存在实时双向数据流，属于强耦合同时求解，是一种全并发的多尺度方法，用于细观↔宏观实时对应研究。目前，由于单向多尺度研究价值有限，且协同多尺度能够完成其内容，加之并发多尺度需要消耗极其庞大的计算资源，因此，协同多尺度分析方法成了学者们研究的重点（除特别说明外，文中其他部分所指多尺度均为协同多尺度）。

自Mayes 等［81］提出基于组分本构的纤维增强复合材料多尺度失效准则研究损伤演化后，众多学者后续开展了大量的研究，近年来取得了许多重要成果。围绕纤维增强复合材料损伤演化多尺度表征与强度分析，Laurin 等［82］通过在细观尺度上引入基体黏性描述剪切载荷下的非线性行为，提出了基于单向板力—热性能的复合材料层合板损伤演化和结构失效多尺度预测方法，并对完整板和开孔板的强度进行了预测。朱国华等［83］则将多尺度方法用到了编织复合材料领域，通过建立T300/环氧树脂编织复合材料单胞模型，预测了层合板三维工程弹性常数，基于此，应用宏观Chang-Chang 失效准则，完成了碳纤维增强复合材料车架损伤分析。Saboktakin 等［60］也完成了类似工作，不同的是宏观失效采用了Hashin失效准则。李星等［84］考虑纤维的拉压失效、基体的膨胀和扭曲失效，建立了基于RVE 的多尺度失效准则，而后通过IM7/5250-4 层合板拉伸试验进行了有效性验证。Massarwa等［85］则提出了基于参数化高保真广义单元格（High Fidelity Generalized Method of Cells，HFGMC）细观模型与有限元二次开发结合的三维多尺度损伤建模方法，且宏观失效采用了Tsai-Wu 失效准则，用于预测结构损伤演化，并生成层合板宏观失效模式。Jong［86］在其论文中详细分析了纤维增强复合材料RVE 中初始孔隙对层合板破坏的影响，发现在纯剪切加载下，层合板剪切强度及断裂能均会随着孔隙的增加而降低。贺春旺等［87］针对三维编织复合材料提出了细观—中观—宏观多尺度失效准则，采用UMAT进行实现，数值计算结果与试验结果非线性表现一致。这种非线性行为在单向板本构曲线中也存在。在宏观尺度上，由于单向板失效准则将纤维和基体组成的RVE 看作横观各向同性材料，因此难以将纤维和基体材料不同的本构特性表现出来，导致失效和强度预测精度不高。因此，需要在细观上对其加以区分，这也是纤维增强复合材料多尺度分析主要在横向加载条件下应用广泛的原因。在细观尺度上，纤维本构表现为线弹性，其拉伸曲线及断裂特征如图4 所示；相反，基体则表现为弹塑性，其拉伸/压缩曲线及断裂特征如图5所示。

图4 纤维拉伸曲线及断裂特征

图5 基体拉伸/压缩曲线及断裂特征

当单向板横向受载时，纤维和基体的模量差很小，导致在该方向上宏观损伤行为会表现出基体的塑性行为，因此，其横向载荷问题变得异常复杂。黄争鸣［91］认为，只要在细观力学模型中计算的是基体真实应力，则任何一个细观力学模型都适用于预测纤维增强复合材料强度。根据世界复合材料失效运动会使用的所有9 种单向复合材料的测量数据，基于桥联模型预测了单向板的刚度和强度，结果表明，桥联模型具有很好的精度。随后，Vignoli 等［92］在横向拉伸强度预测时，假设膨胀能量密度是主要的破坏机制，而对于横向压缩强度预测，主要对界面破坏进行建模。对于横向剪切强度，结果表明基体剪切强度提供了一个很好的近似值。这些结果均采用封闭形式的解析模型给出，为复合材料工程应用领域提供了简单有效的模型。同年，Vignoli 等［93］又对单向板的拉伸强度和剪切强度预测给出了准确的多尺度解析预测模型。在纤维增强复合材料损伤演化多尺度分析领域，一般采用的是含界面的纤维随机分布RVE，如图6所示。因此，纤维随机分布RVE细观受载情况下的损伤演化行为成为纤维增强复合材料多尺度损伤演化与强度分析的重点

图6 纤维随机分布RVE

在纤维—基体界面表征上内聚力模型（Cohesive Zone Model，CZM）得到了广泛的应用，内聚力模型本构种类众多，一般采用双线性牵引—分离本构（如图7）。模型参数需要通过宏观试验获取，Qi 等［95］针对单向板横向拉伸应用多尺度分析，结合扫描电镜和细观力学模型，研究了T800H—基体和T700S—基体的纤维/基体界面强度。纤维在横向加载过程中很难破坏，故仅定义弹性段参数即可。基体屈服过程目前主要采用适合高聚物的Drucker-Prager（D-P）模型，其演化过程可采用延性断裂演化定义［76］［96］。在这一方面，Naya 等［97］根据AS4/8552 纤维增强复合材料的真实截面，通过建立纤维随机分布RVE，计算了横向拉伸、横向压缩、面内剪切和面外剪切四种受载情况下RVE 组分细观损伤演化行为，发现RVE 破坏主要发生在应力集中区域，且主要沿纤维—基体界面扩展。Sharma A 等［98］得到的玻璃纤维增强复合材料二维RVE 损伤演化结果验证了上述规律。同年，他们还完成了双轴加载条件（横向拉伸/压缩—面内剪切）下的三维RVE 损伤演化计算，得到了符合试验结果的损伤演化特征［99］。在上述研究基础上，Han等［100］还对纵向拉伸和纵向压缩加载条件下的纤维随机分布RVE 损伤演化进行了模拟，发现纵向拉伸破坏形式主要为纤维损伤和基体断裂，纵向压缩破坏形式主要为纤维屈曲和基体压溃。基体破坏除D-P模型和延性断裂外，还存在其他定义方式。刘万雷等［101］采用Mohr-Coulomb 模型定义了基体的屈服行为，而Arteiro 等［89］采用了Melro 等提出的基体弹塑性本构。 Chen 等［117］则基于 Gurson-Tvergaard-Needleman（GTN）模型和Johnson-Cook（J-C）模型分别定义了基体的屈服和损伤演化过程。Rueda-Ruiz等［103］考虑动态加载对损伤演化的影响，研究了不同应变率作用下RVE 的损伤演化过程，发现在横向拉伸和面内剪切加载条件下，应变率越高，界面破坏和基体损伤分布越均匀，并通过宏观试验的试件断口扫描结果进行了验证。

图7 双线性牵引-分离本构[94]

任何材料的生产过程都会存在缺陷，纤维增强复合材料生产中容易出现孔隙。考虑孔隙的影响，2022 年，贺春旺等［104］揭示了在横向拉伸、压缩、剪切和纵向剪切四种加载条件下，RVE 中的纤维形状和孔隙对单向纤维增强复合材料强度和破坏机制的影响，发现孔隙会显著降低结构强度，且对其破坏模式有影响（RVE损伤形貌可参考图8）。最近，Daggumati等［105］分析了不同尺寸的孔隙对RVE加载过程中损伤演化的影响，结果发现，大尺寸孔隙和孔隙聚集区确实能够造成应力集中，导致结构破坏，但小孔隙对破坏路径偏移几乎没有影响。

图8 不同受载情况下纤维随机分布RVE细观损伤形貌[104]

上述研究极大地促进了纤维增强复合材料损伤演化多尺度表征与强度预测的发展。然而，对于壳体而言，更加需要关注纤维缠绕复合材料壳体结构损伤演化行为与强度分析。在该领域，祖磊课题组［106］完成了开创性的工作。针对III型复合材料压力容器在爆破试验中的破坏模式，引入RVE 和Puck 失效准则计算复合材料层在爆破试验中的多尺度渐进损伤。结合水压爆破试验，分析了容器的爆破压力和破坏模式。结果表明多尺度模型能够很好地预测复合材料压力容器的破坏行为。2022年，颜勇等［107］针对缠绕复合材料壳体存在的交叉起伏导致壳体宏观爆破强度预测精度不高的问题，通过建立跨纤维随机分布RVE、缠绕菱形区和壳体结构的细观—中观—宏观多尺度强度预测模型，细观上采用基体D-P模型，中观上采用Hashin失效准则，开展了壳体结构细观尺度的渐进损伤失效研究，成功实现了误差仅1.4%的壳体爆破压强高精度预测。此外，Rafiee 和Salehi［108］通过建立两种多尺度模型，分析了纤维分布、纤维间距、纤维邻近度和纤维束波动、交叉、重叠等制造缺陷对纤维缠绕复合材料压力容器爆破强度的影响。结果表明，制造缺陷引起的力学性能局部变化会对爆破强度产生显著影响。

上述研究取得了丰硕的成果，然而，前文已经说明，缠绕张力会对纤维缠绕壳体结构强度造成影响［26］［27］。因此，将缠绕张力耦合到多尺度模型中，是纤维缠绕复合材料多尺度分析计算领域一个需要解决的问题。另一方面，单向板纤维随机分布RVE 的损伤演化特征已经表明纤维—基体界面损伤是复合材料细观损伤的主要模式，宏观破坏由其产生。但目前的纤维缠绕复合材料壳体多尺度研究，还需要结合RVE 对结构细观损伤演化开展更为深入的研究。

4 机器学习在纤维增强复合材料领域应用

一般来说，纤维增强复合材料损伤演化表征及强度预测的数学物理模型较为复杂，且需要消耗大量计算资源。人工智能技术的爆炸式发展使得许多机器学习方法（如多层感知机MLP、自洽聚类分析SCA、BP 神经网络、卷积神经网络CNN、深度学习DP等）被应用于纤维增强复合材料参数预测、RVE 形貌生成和结构强度计算等复合材料力学领域研究中，大大提升了计算效率。2023 年，国家自然科学基金委发布的《可解释、可通用的下一代人工智能方法重大研究计划2023年度项目指南》指出：支持数据驱动与知识驱动融合的人工智能方法发展。建立数据驱动的机器学习与知识驱动的符号计算相融合的新型人工智能理论和方法，突破神经网络模型不可解释的瓶颈。这为机器学习预测纤维增强复合材料结构强度研究按下了加速键。

在这一领域，应用最广泛的当属多层感知机MLP［109］，其基本单元为感知机（见图9），感知机是模仿单个神经元工作过程的基本结构，但内在逻辑完全不同。神经元主要包括树突、轴突和突触等，而感知机则由输入数据、权重、激活函数和输出数据组成。MLP 的网络架构如图10 所示，主要由输入层、隐含层（可含多个）和输出层组成。早在2009 年，Hu 等［111］就基于反向传播神经网络（Back-Propagation Neural Network，NNk）（现称“BP 神经网络”），基于计算结果，通过建立由厚度比、壳体内外温度和缠绕角组成的输入层和仅有爆破强度的输出层NNk，训练了能够预测任意载荷下高压复合贮气III 型气瓶爆破强度的网络模型。Mini 和Sowmya［112］采用纤维取向角、应力比和最大应力对纤维增强复合材料疲劳性能进行分析，而后将有限元计算数据构成输入向量，失效循环次数作为疲劳寿命评估输出参数完成训练，将神经网络模型的预测结果与试验结构进行了比较，验证了网络的可行性。Ammasai Sengodan［19］采用有限元模拟方法对所生成的微结构面内弹塑性响应进行了预测，而后采用主成分分析（Principal Component Analysis，PCA）将细观结构和应力—应变数据投影到低阶空间，利用CNN 学习了上述结果和降低的应力—应变数据。结果表明，经过训练的CNN 能够不依赖复杂有限元计算，实现纤维增强复合材料强度快速预测。Kumar 和Swamy［113］采用ANN 研究了应力水平对玻璃纤维增强复合材料疲劳强度和破坏模式的影响。 通过采用MATLAB 对ANN 进行Levenberg-Marquardt 算法训练，得到的网络预测值与试验结果的相关结果达到了0.99857，充分验证了ANN 建模和预测纤维增强复合材料疲劳寿命的可行性。Wang 等［114］采用基于ANN 的前馈反向传播算法建立了复合材料强度预测模型，对训练集中未采集到的编织复合材料管状结构整体轴压载荷进行了预测。

图9 感知机结构

图10 MLP网络架构[15]

机器学习在复合材料力学性能预测、几何建模和多尺度损伤行为分析领域也发挥了巨大优势。Qi等［115］为解决碳纤维单丝的性能参数难以测试的难题，提出了利用机器学习中的回归树的碳纤维单丝性能变量与纤维增强复合材料宏观性能联系模型。经过碳纤维、基体及宏观结构参数调整和模型选择，得到了泛化性能较好的机器学习模型。Yang等［116］通过RVE 数值计算生成训练数据，而后基于ANN 构建了任意加载下具有客观性的三维非线性弹性材料规律模型，并采用有限元结果与网络预测结果进行对比，验证ANN 在多尺度框架内的有效性。Zhang等［117］实验了一种基于有限元方法的人工神经网络（本质是MLP）用于预测带孔碳纤维增强复合材料层合板在外载荷作用下的强度和渐进损伤行为，并通过仿真结果验证了人工神经网络模型的准确性，实现了层合板失效行为的快速预测。近年来，得益于深度学习的发展，深度卷积神经网络DCNN 在图像、视频、语音和音频处理方面取得了重大突破［118］。Ali等［20］将DCNN 应用到纺织复合材料图像数字孪生领域，通过从单层织物的灰度体积中提取一组原始2D图像切片，使用手动注释的图像来训练DCNN，再使用手动分割图像测试训练后的DCNN，得到超过96%的全局准确率。此外，训练后的DCNN 还可用于从多层织物堆栈中分割不可见图像，具有良好的准确性。考虑纤维增强复合材料多尺度计算中造成的大量资源浪费现象，贺春旺等［16］［119］［120］提出了多种FE-SCA并行多尺度框架。采用该方法对不同纺织结构的力学行为进行预测，发现FE-SCA 能够描述复合材料损伤演化过程，且具有极高的效率和高精度预测能力。

上述研究为机器学习在纤维增强复合材料领域的应用奠定了良好基础。随着纤维复合材料壳体损伤演化多尺度表征和强度预测数学物理模型的发展，实现结构强度的高精度预测指日可待，但同时也会带来巨量的计算资源消耗。鉴于机器学习的计算效率优势和人工智能可解释性的广阔前景［121］，结合高精度的多尺度模型和高效率的机器学习方法，实现纤维增强复合材料尤其是缠绕复合材料壳体结构的快速高精度强度预测，已成为目前亟待解决的问题。

5 未来发展趋势

通过对上述四个方面研究现状的综述，可以发现纤维增强复合材料结构在宏观力学特性参数预测、细观纤维随机分布RVE 生成、跨宏细观多尺度损伤演化表征及机器学习应用方面形成了大量的成果，推动了复合材料多尺度计算力学的发展。未来，会形成以下发展趋势：

（1）单向纤维增强复合材料工程弹性常数作为复合材料力学领域一项重要研究内容，在计算方面主要形成了解析法和数值法。由于解析法快速便利的优势，其在复合材料工程计算和多尺度表征领域仍被大量应用。此外，高精度高效率的数值法应用更加频繁。因此，如何在解析法模型中考虑纤维—基体界面和相互作用，使其具有比肩M-T 模型和数值法的精度；如何结合解析法，加速数值法的计算，是复合材料工程弹性常数预测领域的两个重要发展趋势。

（2）大量纤维随机分布RVE 生成算法的提出极大地推动了纤维增强复合材料细观力学数值模拟及多尺度表征方法的发展。目前的改进算法一味地追求更高的纤维体积分数（有的甚至可达到80%［71］）。但在复合材料实际生产中，即便是航空航天用高标准结构也不会出现如此高的纤维体积分数。日本宇航局对T800H/S 碳纤维单向板纤维体积分数的测试结果为55%［122］；课题前期即使对SYT55S 碳纤维单向板进行纤维加密，得到的纤维体积分数测试结果也并未超过63%。因此，一味地追求高纤维体积分数不仅会造成算法结构更加复杂，也不符合实际。因此，通过改进纤维随机分布RVE 生成算法，使其能够基于简单算法结构生成符合实际情况（纤维截面形状各异、孔隙多元化和纤维局部聚集/稀疏）且纤维体积分数较高的纤维随机分布RVE，推动该领域入门快速化，是必须发展的研究方向。

（3）众多研究成果推动了纤维增强复合材料损伤演化多尺度表征与强度计算的发展，但目前关于缠绕复合材料壳体结构的多尺度表征研究较少。此外，缠绕张力会对纤维缠绕复合材料壳体结构强度造成影响［11］［12］。因此，将缠绕张力耦合到多尺度模型中，是壳体结构多尺度分析计算领域一个需要发展的方向。另一方面，单向板纤维随机分布RVE 的损伤演化特征已经表明纤维—基体界面损伤是复合材料细观损伤的主要模式，宏观破坏由其产生。然而，在目前的壳体结构宏观研究中，复合材料失效理论仅能预测纤维、基体和层间的破坏，无法预测纤维—基体界面破坏。因此，结合细观RVE 对壳体宏观结构开展损伤演化特征的多尺度表征研究，也将成为未来复合材料多尺度表征与强度计算领域的一大趋势。

（4）随着纤维增强复合材料损伤演化多尺度表征和强度预测数学物理模型的发展，实现复合材料结构强度的高精度预测指日可待，但同时也会带来巨量的计算资源消耗。鉴于机器学习的计算效率优势，如何结合高精度多尺度模型的可解释性和机器学习方法的高计算效率，实现纤维增强复合材料尤其是缠绕复合材料壳体结构的快速高精度强度预测，未来也将成为复合材料强度预测领域研究的一大热点。