基于改进相关向量机的锂电池剩余使用寿命预测
2024-03-10侯小康袁裕鹏
侯小康,袁裕鹏,童 亮
(1.武汉理工大学船海与能源动力工程学院,湖北武汉 430063;2.武汉理工大学交通与物流工程学院,湖北武汉 430063;3.国家水运安全工程技术研究中心,湖北武汉 430056)
为节约能源和降低排放,交通领域正在大力推进电动船舶和电动汽车的发展。由于锂电池具有高能量密度、强环境适应性和强荷电保持能力的特点,被广泛应用于设备的储能或动力系统中[1]。然而,随着充放电循环不断进行,锂离子电池内部的物理化学结构逐渐变化,严重影响电池的性能与安全。近年来,锂离子电池快充技术和储能技术发展迅猛,这使得电池性能衰退状态的准确评估和综合管控问题面临更大挑战,电池故障风险加剧[2]。准确预测剩余使用寿命(RUL)可提前获知电池性能退化信息,确保电池运行的安全性和效率。
锂离子电池RUL可定义为在一定的充放电规则下,电池目前可用容量下降到额定容量的70%或80%时所经历的充放电循环次数。目前,国内外研究人员对于锂离子电池RUL预测的方法可分为以下三种:模型法、基于数据驱动的方法和基于融合模型的方法。
模型法通常采用自适应方法,如卡尔曼滤波(KF)[3]和粒子滤波(PF)[4]等,对建立的电池电化学模型(EChM)或等效电路模型(ECM)进行参数辨识[5],进而基于模型参数与剩余使用寿命的映射关系预测电池RUL。Ramadesigan 等[6]基于电化学理论搭建了电池的伪二维模型(P2D),通过求解P2D 模型参数,较为精确地估计了容量下降趋势;Wassiliadis 等[7]使用双重扩展卡尔曼滤波器(DEKF)对电池状态和相关参数进行了预测,结果表明在电池荷电状态和模型参数的预测方面具有可靠的性能,然而这种方法在电池高退化状态时电池容量的预测值将偏离实际值。为了解决这个问题,Zhang 等[8]开发了一种容量损失模型,该模型与固体电解质界面层生长和活性材料损失的老化机制相耦合,使用递推最小二乘法计算模型参数,结果表明:估算的容量损失误差小于1%。对于PF 方法,重要性函数和采样粒子的退化会影响预测精度。因此,Zhang 等[9]提出了基于线性优化组合重采样的无迹卡尔曼滤波器(UKF),以提高RUL的预测精度。通过UKF 得到建议分布,作为PF 的重要性函数。此外,基于线性优化组合重采样算法以增强采样粒子的多样性。与标准PF 和无迹PF 算法相比,所提出的方法可以提高预测精度。模型法中的电路模型参数和自适应方法参数等参数繁多,计算成本巨大,且模型鲁棒性和泛化能力有限,适用于离线分析,不适用于工程实际。
随着大数据技术和人工智能产业的发展,数据驱动方法已被应用于预测电池RUL。该方法将电池视为黑箱,借助大量可测量的电压、电流和温度等数据来分析电池内部特性。常用的数据驱动算法包括神经网络(NN)[10]和相关向量机(RVM)[11]等。Shen等[12]提出了一种基于部分充电周期内电压、电流和充电容量测量的锂离子电池容量在线估计的深度卷积神经网络(DCNN)模型。DCNN 模型能够从大规模数据集中学习电池的复杂可测量数据与电池容量之间的关系。结果表明,预测值的最大百分比误差可控制在5%以内,均方根误差在0.5%以下。然而,文献[12]所提出的DCNN 模型仍然存在一些局限性,例如环境温度设为恒定,未考虑温度变化而导致的电池容量变化等。为了解决这一问题,Guo 等[13]提出了一种基于充电健康因子提取和改进RVM 的锂离子电池容量估计方法。通过灰色理论分析,从电池充电电流、电压和温度中提取了14 种健康因子(HF),并使用主成分分析法筛选出高度相关性的健康因子,作为RVM 模型的输入,结果显示电池容量估计均方误差为1.3%;Kodjo 等[14]基于多年来收集的真实电动汽车数据,使用随机森林机(RF)方法进行容量估计、老化预测和相关老化因素排名,研究结果表明容量估计的平均百分比误差为1.27%;Wei 等[15]基于粒子群算法和最小二乘法支持向量机建立了电池的RUL预测模型,结合实时状态数据,使得RUL预测值的误差在4%以下。
近年来,基于融合模型的方法正成为该研究领域的热点。此方法融合了多种算法的优点,主要包括模型融合和数据融合。为改善数据驱动方法中结果准确性较低和可信度不高的问题,Ma 等[16]提出了一种基于CNN 和长短期记忆循环神经网络(LSTM RNN)的融合模型来完成RUL预测;Zhao 等[17]开发了一种基于深度置信网络(DBN)和RVM 融合的RUL预测方法。DBN 从电池退化数据中提取特征,并将特征输入到RVM 中进行RUL预测,提高了DBN 长期预测能力和不确定性表达能力;Ma 等[18]为了克服神经网络中复杂的结构参数设置求解和电池数据集规模不断增大的问题,创造性地开发了宽度学习-极限学习机(BL-ELM)的融合模型,以电池的11 个特征数据作为输入,以容量和循环寿命作为输出,结果显示,RUL预测的平均绝对误差在10%以下。基于融合模型的方法可以改善模型法的建模难度大等问题,还可以提高数据驱动方法的适应性,但目前该方法也存在计算成本高、参数设置复杂等问题[19]。
在基于数据驱动算法和融合模型的方法中,电池退化特征提取是关键之一。作为动力源的电池组在工作时通常分为充电工况和放电工况。放电工况随着实际工况复杂多变,放电电压和电流等也因此而动态变化,退化特性分析困难。因此,现阶段常利用电池充电数据提取退化特征或建立老化模型。刘栋[20]从电池充电数据中直接提取恒压阶段充电平均温度和充电容量等作为退化特征,利用机器学习算法评估电池退化水平,这是直接提取特征法;现阶段,常用的间接提取特征方法有电化学阻抗谱(EIS)、容量增量分析法(ICA)和差分电压分析法(DVA)等。内阻是评价电池性能退化水平的重要指标,EIS 技术通过使用特定峰值阻抗谱来提取电池的退化特征因子[21]。ICA 和DVA 分别从电池充电电流、充电电压和时间变量中提取出电量增量曲线和差分电压曲线[22-23],进而可以通过分析两种曲线的变化来提取退化特征、建立老化模型,应用较为广泛。但ICA 和DVA 抗干扰能力较弱,退化特征易消失。代表特定化学反应的差热伏安法(DTV)峰值参数也可用于探索电池老化过程[24]。差分应力参数(DMP)分析是对电池退化特征提取和老化建模方法的补充[25]。Cannarella 等[26]开发了一种基于DMP 的方法,通过应力测量来估计电池容量状态,与复杂的估计模型相比,应力和电池容量之间简单的线性关系具有明显的优势。上述间接提取特征方法通常需要复杂的实验条件和步骤,或者需要高精度传感器测量微小电流,不适合在线提取电池退化特征。
目前,基于数据驱动的锂离子电池剩余使用寿命预测方法有很多,在实际应用中,锂离子电池的全寿命周期数据较少,并且难以获得,不属于大样本问题,并且需要对预测过程中的不确定性进行量化。此外,在预测过程中,实验误差和数据噪声等不确定性来源会造成寿命预测困难、预测结果置信区间大等问题。针对上述问题,本文提出了基于变分模态分解(VMD)和贝叶斯优化(BAO)的多核相关向量机(HRVM)模型。使用VMD 解决数据异常点对预测精度的影响和电池容量再生问题;使用BAO 算法对组合核函数的相关参数进行优化,解决单次预测和参数设置的高随机性问题,提高HRVM 的长期预测能力;使用HRVM 处理小样本问题,量化了剩余使用寿命预测中的不确定性,提高了模型的预测精度。利用美国国家航空航天局(NASA)和Oxford 锂离子电池数据集,验证了所提出模型的有效性。
1 锂离子电池数据集
采用NASA PCoE 提供的容量为2 Ah 的18650 锂离子电池老化数据集[27]和Oxford 提供的容量为0.740 Ah 的锂离子电池循环数据集[28]。NASA PCoE中心的实验台架如图1 所示。

图1 NASA PCoE中心电池实验平台[29]
在NASA 电池循环充放实验中,采用恒流恒压模式充电,并以恒流模式进行放电。当电池容量降至额定容量的70%时,则视为到达电池寿命失效阈值,实验终止。选用循环工况不同的B5 和B6 号两节电池作为研究对象,两节锂离子电池的容量退化曲线如图2 所示。

图2 NASA电池容量退化曲线
Oxford 电池循环实验使用容量为0.740 Ah 的软包锂离子电池。保持电池温度恒定为40 ℃,采用恒流或伪开路电压循环模式充电,并从Artemis 城市循环工况获得放电曲线。每经历一定次数的循环对电池进行一次表征测量,直到电池容量降至额定容量的80%。考虑数据可用性,选取C2 号电池作为研究对象,其容量退化曲线如图3 所示。

图3 Oxford电池容量退化曲线
2 VMD-BAYES-HRVM 方法的建立
2.1 健康因子分析及提取
锂离子电池的循环寿命在使用过程中会不断减少,但剩余寿命次数却难以直接测量。因此,从可监测的间接性参数入手,利用从电池的充电数据中提取的电流、电压等可直接测量量作为健康因子,间接评估电池的剩余使用寿命。以B5 号电池为例,分别提取第35 次、第70 次、第105 次和第140 次循环的充电过程中的特性曲线,如图4 所示,分析充电过程中电池温度、充电电流和电压的变化趋势。

图4 循环实验中B5号电池充电特性变化曲线
峰值温度到达时间:NASA 电池老化数据集的环境温度为24 ℃,随着充电过程的进行,电池监测温度先上升后下降,如图4(a)所示,随着充电循环次数的增加,峰值温度时间会不断提前,因此,提取充电过程中的峰值温度到达时间作为评估电池RUL的健康因子,记为HF1。
恒压阶段等电流差充电时间:随着充放电循环次数的不断增加,充电过程中的电流曲线也随之变化,如图4(b)所示,考虑到在实际使用过程中,存在不完全充电的情形,提取恒压阶段电流值从1.5 A 下降1 A 的时间间隔,作为评估电池RUL的健康因子,记为HF2。
恒流阶段等电压差充电时间:同样地,随着充放电循环实验的不断进行,充电过程中的电压曲线也随之变化,如图4(c)所示,考虑充电开始时刻电压起始值的不同,提取恒流阶段电压从3.8 V 升至4.2 V的时间间隔,作为评估电池RUL的健康因子,记为HF3。
充电阶段平均充电电压:由图4(c)可知,随着电池不断地充放电,充电过程中电池电压上升至4.2 V的速度不断提高,充电电压的平均值也逐步增大,计算充电过程中的平均充电电压,作为反映电池RUL的因子,记为HF4。
此外,锂离子电池容量下降曲线也能反应电池老化水平,因此将锂离子电池的容量衰退数据记为HF5。
因为Oxford 电池实验是保持电池温度恒定,且未对电流数据进行监测,所以健康因子只提取出与电压相关的HF3、HF4 和与容量相关的HF5。
为检验所提取健康因子的有效性,利用Spearman 系数分析HFs和RUL的相关性。Spearman 系数可以用来评估所提取的健康因子与电池剩余使用寿命之间的单调关系,且不受外界实验条件的干扰,可以很好地反映HFs与RUL之间的相关性。
上文提取的两节锂离子电池的HFs与RUL之间的相关系数如表1 所示。
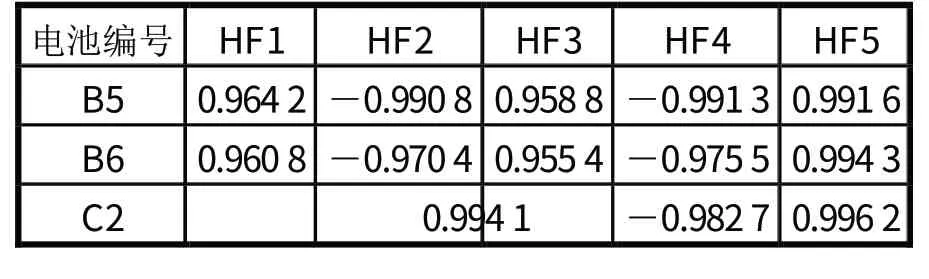
表1 HFs 与RUL 间的相关系数结果
由表1 可知,所提取的健康因子与电池剩余使用寿命的相关系数的绝对值均在0.95 以上。这表明HF1、HF2、HF3、HF4 和HF5 均能够有效地反映锂离子电池循环寿命衰退的趋势。
2.2 多核相关向量机
RVM 是一种基于贝叶斯理论的稀疏概率模型[30]。假定给出数据集,其中xi是预测模型的输入向量,本文即为提取的5 种健康因子;ti是模型的目标变量,为锂离子电池的RUL,则ti的条件概率分布可表示为:
式中:β是模型噪声;K(x)是核函数;ω=(ω1,ω2,...,ωn),为核函数相对应的权重;y(x)为线性模型的均值。
为求解上述模型,首先需求出权重ω的后验概率分布,进而求得βnew和权重ωi对应的精度αinew,直至满足收敛条件。
核函数的选取是构建优秀的RVM 回归模型的关键之一。高斯核函数在处理非线性关系时,有着良好的逼近能力;拉普拉斯核函数鲁棒性和收敛性较好。结合以上分析和仿真实验结果,本文选取高斯核函数和拉普拉斯核函数组成多核相关向量机预测模型的混合核。
2.3 贝叶斯优化方法
多核相关向量机回归模型中两个核函数各自的权重w、高斯核函数参数γ1=1/和拉普拉斯核函数参数γ2=1/σ2四个参数对RUL回归模型的预测效果有着重要的影响。为得到更优秀的回归模型,需要寻找出这些参数的最优值以最大化预期目标。贝叶斯优化是一种黑盒优化算法,可用来求解表达式未知的函数的极值问题。它的优势在于可基于已探索点的信息来判断下一探索点的位置,这使得贝叶斯优化的效率大大提高,时间成本低,粒度较小。综合考虑RUL预测模型的精确性和时间成本,本文选用贝叶斯优化算法对多核相关向量机回归模型进行优化,优化流程如图5 所示。

图5 贝叶斯优化流程图
对RUL预测模型的训练过程中,选取均方根误差(RMSE)作为贝叶斯优化的目标函数。通过不断地更新优化RUL预测模型中高斯核函数的权重w1、参数γ1和拉普拉斯核函数的权重w2、参数γ2,获得更优的RMSE值。RMSE定义式如下:
式中:n表示样本的数量;表示锂离子电池第i个循环剩余使用寿命的预测值;RULi表示第i个循环的实际剩余使用寿命。
以B5 号电池为例,将迭代次数设置为150 次,在模型训练过程中,贝叶斯优化参数过程如图6 所示。

图6 贝叶斯优化迭代过程
从图6 中可以看出,在贝叶斯优化过程中,迭代30 次时,RMSE就基本达到了最优值。此外,在每次迭代的过程中,除极个别点外,RMSE的观测值和估计值十分接近。
2.4 变分模态分解
变分模态分解是一种自适应、非递归的模态变分和信号处理的方法[31]。VMD 约束变分模型如下式表示:
式中:K为需要分解的模态个数;δ 表示狄拉克函数;ωk和uk分别为分解后的第k个中心频率和模态分量;*表示卷积运算。
为求解式(6),引入拉格朗日乘法算子λ,得到增广拉格朗日表达式,进而可以求解得到和
式中:σ为惩罚因子;λ为拉格朗日乘子。
选择模态分解个数K=6,以B5 号电池为例,HF1的VMD 处理结果及处理后数据和原始数据的相关系数如图7 所示。

图7 B5号电池HF1 VMD处理结果图
由图7 可知,VMD 在分解RUL模型输入数据(HF1)的过程中,分别产生了5 个内涵模态分量(IMF)和1 个残差(Res)。其中,IMF1~IMF3 波动较为剧烈,反映了锂离子电池的高频容量再生现象;IMF4~IMF5 变化则相对平缓。IMF1~IMF5 共同反映了电池衰退过程中的容量波动和循环实验时的噪声干扰。使用皮尔逊相关性分析法计算原始数据与残差之间的关系,结果在0.98 以上。以上分析表明残差在消除电池容量再生现象所带来的数据噪声的同时,也可以很好地保留原始数据的主要信息。
2.5 VMD-BAYES-HRVM 方法
将提取的五个健康因子作为输入,将锂离子电池的剩余使用寿命作为输出,建立用于RUL预测的VMD-BAYES-HRVM(简称V-B-HRVM)模型。使用VMD 对模型输入数据进行平滑滤波,降低数据噪声,利用BAYES 优化算法对HRVM 的核函数权重w以及相关参数进行寻优,其详细流程如图8 所示,模型主要步骤如下:
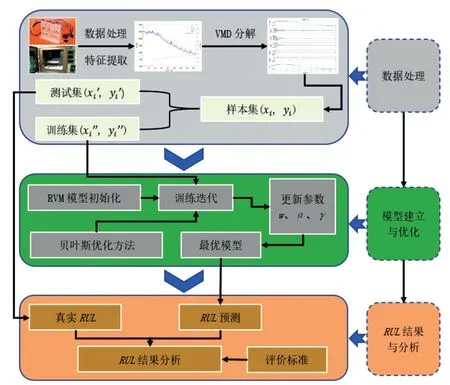
图8 基于V-B-HRVM的锂离子电池RUL预测流程
(1)数据处理:使用VMD 技术对前文提取的HFs进行去噪处理,并将处理后的数据分为训练集和测试集,为后续模型训练和测试提供数据支撑;
(2)模型建立与优化:选择高斯核函数与拉普拉斯核函数作为混合核建立HRVM 模型;选择RMSE作为目标函数,设置迭代次数为150 次,使用贝叶斯优化算法对混合核中各核函数权重w1、w2和参数γ1、γ2进行迭代寻优;
(3)RUL结果预测与分析:使用NASA 电池数据集中的B5 和B6 号电池进行仿真验证,选择RMSE和平均绝对误差(MAE)作为评价标准,对不同循环寿命处的RUL预测结果进行分析,并将所提出的方法与其他方法对比。
3 案例分析
3.1 评价标准
为了评价V-B-HRVM 方法的性能,使用MAE、RMSE作为评价标准来验证所提出方法的有效性。RMSE定义与前文中的一致,MAE表示模型预测值与真实值间距离的平均值,它用于反映预测结果的整体准确性:
3.2 案例验证与分析
在前文的研究中,建立了基于HRVM 的锂离子电池剩余使用寿命预测模型,通过输入提取的健康因子,进而得到RUL的预测值。因此,RUL预测模型的精度依赖于模型输入与循环次数之间非线性关系的强弱。为分析所搭建模型在电池寿命周期内对RUL的预测能力,选择电池循环寿命数据的60%处为预测起始点。由于C2 号电池寿命终止点位于循环数据的前60%,故此次仿真只选用B5 和B6 号电池。图9~10 为对应的RUL预测结果和相应的预测误差的变化趋势,表2~3 分别是混合核核函数参数寻优值和预测结果统计。

表2 模型参数优化结果(前60%数据作为训练集)
由图9 可知,真实RUL线性单调递减,所提出模型的RUL预测值贴近于RUL的真实轨迹。两节电池的RUL预测误差也均在合理的范围之内。在预测过程的开始时,RUL预测值在真实值附近波动,且真实值落在预测值的95%置信区间内;在预测过程的后半段,RUL预测值逐渐偏离真实值,预测误差也进一步加大,这是因为在后半段,模型输入与锂离子电池循环次数之间的非线性关系逐渐减弱。B5 和B6 号电池的终止寿命点(EOL)分别为125 次循环和108 次循环。由表3 可知,B5 和B6 号电池的EOL预测值分别为124 次和107 次循环,跨度区间分别为[123,126]和[60,61]。

表3 模型预测结果(前 60%数据作为训练集)
从图10 可以看出,B6 号电池预测结果的95%置信区间比B5 号电池的更窄,这表明B6 号电池预测结果的不确定更小,预测值的可信度更高。但B5 号电池的EOL真实值落在预测值的95%置信区间内,而B6 号电池则落在95%置信区间之外。此外,B5 和B6 号电池的RMSE分别为4.09 和6.86 次循环,MAE分别为3.12 次和4.87 次循环。以上结果表明V-BHRVM 模型有可靠和准确的RUL预测能力。

图10 前60%数据作为训练集时电池RUL预测误差
为进一步检验所提出模型的准确性和鲁棒性,基于B5、B6 和C2 号电池容量数据所搭建的寿命衰退模型被用来预测在寿命衰退早期阶段的RUL。预测起始点对应的寿命衰退阶段越早,用来构建RUL预测模型的训练数据越少,RUL预测结果的不确定性越明显。选取B5、B6 和C2 号电池循环寿命次数的前40%作为预测模型的训练数据,即预测起始点分别是第67、68 和29 次循环,预测结果及核函数参数寻优值如图11~12 和表4~5 所示。

表4 模型参数优化结果(前40%数据作为训练集)
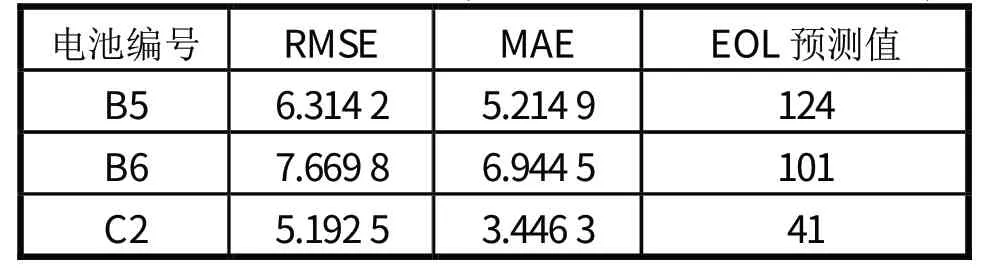
表5 模型预测结果(前40%数据作为训练集)

图11 前40%数据作为训练集时电池RUL预测结果
从图11 中可以看出,电池B5、B6 和C2 的RUL预测值一直在真实值的附近上下波动,能够准确反映RUL真实值的轨迹,电池B5、B6 和C2 的EOL预测值分别为124 次、101 次和41 次循环,预测误差分别是1次、7 次和2 次循环。EOL预测结果的95%置信区间分别为[122,126]、[100,102]和[40,42],这表明RUL预测结果的不确定性较小,所建立的模型在锂离子电池寿命衰退早期阶段的RUL预测中具有很高的可信度。而且观察图12 可知,RUL误差跨度在整个预测过程中都保持稳定,且B6 号电池的预测结果95%置信区间跨度整体上小于B5 号电池。C2 号电池RUL预测曲线后半段的离散程度较大,这是因为实验后期C2 号电池老化幅度较大,且容量再生现象加剧,所提取的HFs与RUL之间的非线性关系减弱,但预测结果的RMSE和MAE仍维持在较为理想的范围内。上述结果表明所提出的方法对循环工况不同、类型不同的电池有着较高的RUL预测精度。

图12 前40%数据作为训练集时电池RUL预测误差
为验证所提出方法的优越性,将V-B-HRVM 方法与B-HRVM 和RVM 进行比较,选用B6 号电池,所有模型的预测起点设置为101 次循环。在V-BHRVM 和B-HRVM 方法中,核函数均选为高斯核和拉普拉斯核,优化迭代次数均为150;在单RVM 方法中,核函数选为高斯核。三种方法的RUL预测结果和误差如图13~14 所示,预测结果统计见表6。
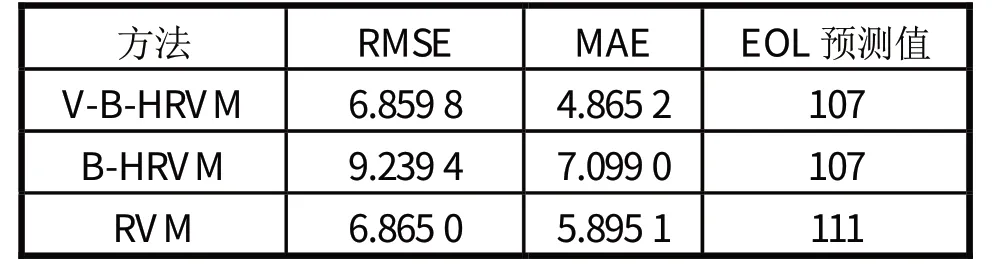
表6 三种方法模型预测结果

图13 前60%数据作为训练集时三种方法B6号电池RUL预测结果对比
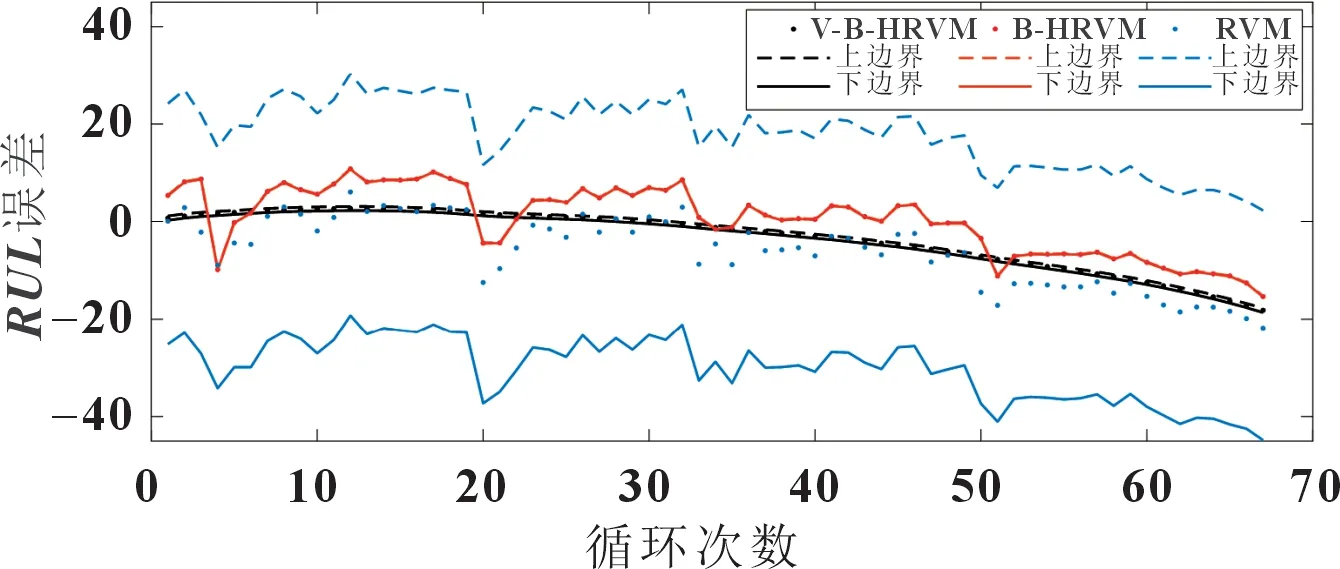
图14 前60%数据作为训练集时三种方法B6号电池RUL预测误差对比
图13 显示了所提出的方法和其它两种方法之间的预测结果对比。由图13 可知,V-B-HRVM 的预测结果更接近RUL真实值。B-HRVM 方法的预测结果的RMSE和MAE分 别 为9.24 和7.10,相 比于V-BHRVM,分 别 增 加 了34.69% 和45.91%。RVM 的RMSE和MAE分 别 为6.87 和5.90,相 比 于V-BHRVM,分别增加了0.08%和21.17%。以上结果表明,相较于其它两种方法,V-B-HRVM 有着更为可靠和准确的锂离子电池RUL预测性能。B6 号电池的真实EOL为108 次循 环,V-B-HRVM 的EOL预 测值为107 次循环,跨度区间为[107,108];B-HRVM 的EOL预测值为107 次循环,跨度区间为[107,107];RVM 的EOL预测值为111 次循环,跨度区间为[84,132]。相较于B-HRVM,V-B-HRVM 方法EOL预测值的95%置信区间包含着EOL真实值,准确性更高;相较于RVM,在精度更高的同时,V-B-HRVM 的EOL预测结果跨度区间更窄,这表明所提出方法的预测不确定性更小,性能更为稳定。
4 结论
针对小样本条件下锂离子电池剩余使用寿命预测的难题,本文基于变分模态分解原理和贝叶斯优化思想,设计了基于多核相关向量机的锂离子电池剩余使用寿命预测模型,使用MATLAB 仿真软件进行了案例验证。
从工况稳定的充电循环中提取了健康因子HF1、HF2、HF3、HF4 和HF5,Spearman 相关性分析结果表明,HFs 和RUL间的相关系数绝对值均在0.95 以上,从而验证了所提取的健康因子的可靠性。
当以60%循环寿命数据作为预测始点时,B5 和B6 号电池的RUL预测结果的MAE分别为3.12 次和4.87 次 循 环,RMSE分 别 为4.09 次 和6.86 次 循 环,EOL预测误差均为1 次循环;当以40%循环寿命数据作为起始点进行早期剩余使用寿命预测时,RUL预测结果的MAE分别为5.21 次、6.94 次和3.45 次循环,RMSE分别为6.31 次、7.67 次和5.19 次循环,EOL预测误差分别为1 次、7 次和2 次循环。以上结果均表明,所提出的V-B-HRVM 方法表现出了较为优秀的RUL预测能力。
V-B-HRVM 的预测结果在不确定性较小的情况下,相较于B-HRVM 和RVM,MAE分别下降了31.47%和17.47%,有着更高的准确性。
在未来的工作中,将进一步优化算法框架,研究更有效的电池健康因子提取方法,使算法更加满足工程实际应用的需要。
