浅谈数显测高仪的测量不确定度评定

王恪聿，徐央，卢鼎，蔡敏旭

（浙江方圆检测集团股份有限公司，浙江 杭州 310018）

数显测高仪是一种立式单坐标数字化几何量计量仪器，常以光栅、容栅或磁栅作为测量元件。测高仪以自身较高的测量精度常在现代化工业测量中发挥重要作用，其常用于精加工零部件的长度尺寸、几何面之间的距离及孔轴直径。在实际的测量校准工作中，常需提供仪器的示值误差及不确定度，而现有测高仪工作手册及产品使用说明书并未给出这一数值。本文现以日本三丰公司生产的LH-600E 型数显测高仪为例，对该型号测高仪600mm 校准点的示值误差进行不确定度评定，以研究分析不确定度的评定过程和其中影响要点。

图1 数显测高仪

1 校准方法与数学模型

数显测高仪可对三等量块进行直接测量实现校准工作。参照测高仪检定规程JJF 1254-2010 结合LH-600E 型测高仪使用手册说明，仪器最大允许误差为（1.1+L/600）μm（L 为测量长度，单位mm），该允许误差仅可在温度（20±0.5）℃、相对湿度为（50±5）%RH 有效，故将测高仪与量块置于00 级平板上并于恒温室静置24h。

正式校准开始时，先以平板设置测高仪参考位置并设置为“0”位，使用测高仪在无气浮状态下测量量块长度，于校准点测量3 次，取平均值作为测量值l，标准量块的实际长度为L，则被校准点位示值误差△L 为：

测量过程中引起不确定度的来源见表1。

表1 测量不确定度来源

确定校准点位示值误差不确定度的数学模型为：

其中，e 为数显测高仪示值误差；La为数显测高仪示数；Lb为量块标称值；△Ta为数显测高仪偏离标准温度值；△Tb为量块偏离标准温度值；αa为数显测高仪热膨胀系数；αb为量块热膨胀系数。

2 数显测高仪不确定度评定

2.1 不确定度类型及分布因子确定

测量不确定度一般由若干分量组成，每个分量用其概率分布的标准偏差估计值表征，称标准不确定度。对被测量进行独立重复观测，通过所得到的的一系列测得值，用统计分析的方法获得试验标准差的方法为A类标准不确定度评定方法。根据有关的信息或经验，判断被测量的可能值区间，假设被测量值的概率分布，根据概率分布和要求确定置信因子的方法为B 类标准不确定度评定方法。数显测高仪各不确定度类型及分布因子见表2。

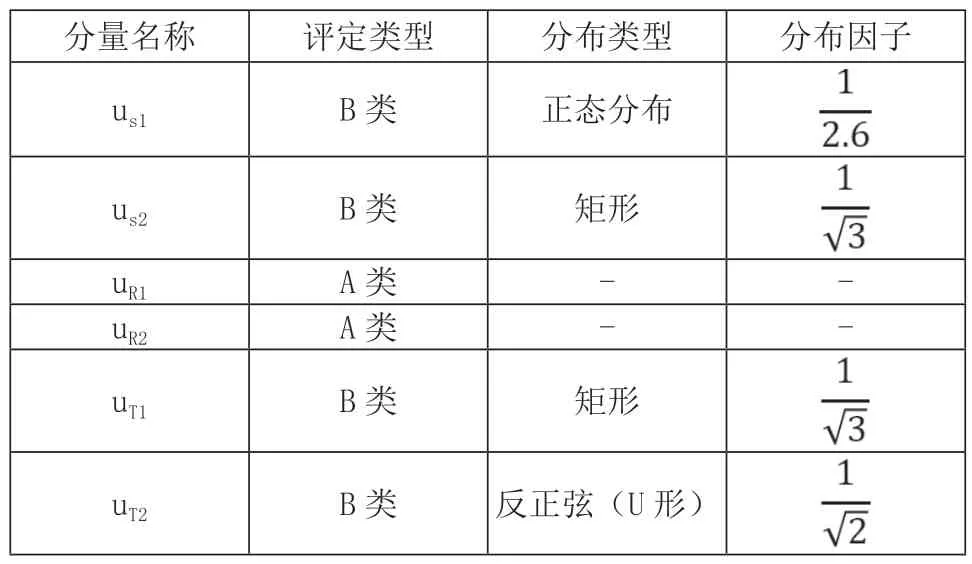
表2 测量不确定度类型及分布因子

2.2 量块中心长度测量引入的不确定度

量块中心实际长度及认定的测量不确定度以校准证书为准，由证书得知，长度为600mm 的3 等量块测量不确定度Us1=0.7μm，该不确定度包含因子为k99=2.6，则引入的量块中心长度测量不确定度为：

2.3 触点位置偏离量块中心引入的不确定度

在使用测高仪测量量块时，采用接触式测量方式，该测量方式会导致触头未触及量块中心位置导致产生不确定度，有经验的操作人员可将触点接触于量块中心端直径σ 的1mm 内，该圆内任一位置均可能被触头所触碰，服从矩形分布。查阅校准报告可得600mm 的3 等量块长度变动量t 最大为0.40μm，量块工作面的有效宽度b为9.0mm，由此触点位置偏离量块中心测量不确定度为：

2.4 数显测高仪重复性/测量分辨力引入的测量不确定度

测高仪的重复性会引入测量不确定性，对于该A 类不确定度，需通过一系列观测值经统计计算获得，使用被校测高仪连续测量10 组重复性示数，测量值见表3。针对该类计算，选用贝塞尔公示计算试验标准偏差s 为：

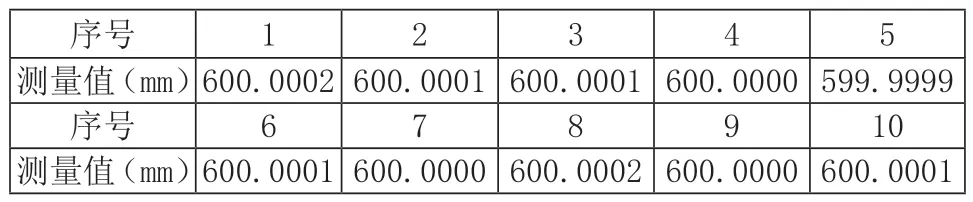
表3 测高仪重复性试验数据

校准时每个测试值测量3 次取平均值作为检测结果，则数显测高仪重复性不确定度为：

除测高仪示值重复性引入的不确定因素外仍存在仪器自身数字分辨力所引入的不确定度uR2，所校仪器LH-600E数显测高仪的数字分辨力为0.1μm。则不确定度为：

由于测高仪重复性不确定度与数字分辨力不确定度互为包容关系，则该A 类不确定度取大者作为有效值，因此：

2.5 量块与数显测高仪温差引入的不确定度

量块为钢制，其线性热膨胀系数为11.5×10-6℃-1。在测量前已将待校数显测高仪与量块置于同一环境24h，二者温差△T 不超过0.1℃，以保守计算取大值0.1℃作为温差计算量。量块与数显测高仪温差不确定度服从矩形分布，则量块和测高仪由于温差引入的不确定度为：

2.6 量块与数显测高仪热膨胀系数引入的不确定度

所校数显测高仪为钢制，标称线性热膨胀系数为11.5×10-6℃-1，但由于实际加工材质区别，假定量块与数显测高仪的热膨胀系数相差值为1×10-6℃-1，该引入的不确定度服从反正弦分布。恒温室控制温度为（20±0.5）℃，当前假定温度偏差为最大值即0.5℃，则不确定度为：

2.7 合成标准测量不确定度

数显测高仪测得值为通过测量量块直接获得，即测量模型为y=x，且各测量不确定度分量间互不相关，至此，合成标准不确定度为：

代入式前计算所得各不确定度分量值得：

2.8 扩展测量不确定度

扩展不确定度是指被测量可能值包含区间的半宽度，在常规的工作中需提供该数值。扩展不确定度U 由合成标准测量不确定度uc乘包含因子k 得到，其公示为：

数显测高仪测得量的概率分布近似为正态分布，当包含因子k 取值为2 时，则由U=2uc包含的测量结果区间[y-U，y+U]拥有95%的包含概率。在此计算下扩展不确定度值为：

3 试验过程分析

通过对测高仪的不确定度评定整个过程进行回溯，可发现由量块中心长度测量不确定度、量块与测高仪温度差和量块与测高仪线性膨胀系数差导致的B 类不确定度在数值上大于由测高仪重复性和测高仪测量分辨力导致的A 类不确定度。分析可得，A 类不确定度属仪器设备自身特性，该特性不易受外界因素影响而产生变动。反观B 类不确定因素，该类因素值较大受制于环境和测量等外界干扰，从而导致结果值放大。

针对本次测高仪的不确定度评定而言，仅量块与测高仪温度差这一干扰项就占据了设备整体不确定度的较高百分比，因而在实际高精密测量环境下，有必要对试验环境进行监测，并使待测样品与测量仪器置于同一环境保持较长时间。对总体不确定度占比较高的另外因素为量块中心长度测量不确定度和量块与测高仪线性膨胀系数。其中，量块与测量设备的线性膨胀系数为固有值，在测试实验室采购器材后属较难调整项。针对量块中心长度测量不确定度这一因素，可采取使用稳定性高、线性膨胀度低的陶瓷量块、大理石量块或采用精度等级更为高的钢制量块以降低不确定度。

4 结语

由前述各不确定度分量的计算可得，由测量温度引入的不确定度分量对总不确定度量值影响最大。对于该影响，实际校准测量工作中在确保成本可控、测量间温度均匀可靠的情况下，应尽量使测高仪与待测量样品置于同一环境足够时间，以降低温度偏差造成的测量不准确，同时多次测量，通过数学计算方式进一步降低测试误差。

现代社会科技日益发展，市面上已出现了一些自带温度补偿修正功能的量仪，该类仪器具有对环境及样品进行差异化修正功能，进一步降低测量不确定度。随着该类新设备的运用普及，可进一步提升检验检测工作效率并提升测量精度。