河南省年季降水集中度研究
2024-03-08吴奕李飞李超群
吴奕, 李飞, 李超群
(1.河南省水文水资源测报中心,河南 郑州 450003; 2.南水北调中线实业发展有限公司,北京 100038;3.黄河勘测规划设计研究院有限公司,河南 郑州 450003)
河南省地跨海河、黄河、淮河、长江四大流域,是我国少见的多流域聚集省份。由于不同流域气候条件一般不相同,河南省降水分布呈现出较为复杂的时间和空间差异[1-2]。近年来,人类活动影响和气候变化一定程度上改变了全省的水文循环过程,导致降水时间分布特点随之发生变化[3-4]。对长系列的气象资料研究结果表明,河南省年降水量呈减少的趋势[5],从降水量年内分配的变化趋势来看,豫南地区春季降水量减少趋势明显[6],汛期日降水量增加,出现了诸如2021年郑州“7·20”极端暴雨事件[7]。在此背景下,通过对河南省降水的时间均匀特征进行研究,明晰降水的年际、年内分布规律,对于水资源时空调节、水旱灾害防御具有重要的意义[8-9]。
针对河南省降水时间分布研究,一般多着眼于探求多年变化特征,如史佳良等[10]、刘晓璐等[11]、商东耀等[12]利用标准降水指数等多种指标采用Mann-Kendall等多种方法统计分析了近年来降水时间分布年际变化特征。既有研究对于降水年内时间分布规律的探究较少,一般多基于少量气象站点资料采用标准化降水指标等进行分析研究[13-14]。由于资料可获得性受限,采用多流域大数量水文站点数据资料进行全省多流域降水年内时间均匀特征研究较少。目前对降水年内时间均匀特征研究广泛采用的是降水集中指数(Precipitation Concentration Index,PCI)[15-16]和降水集中度(Q)[17-18],缺少与河南省相关的深入应用研究。
本文基于河南省全省范围内4个流域522个雨量站点资料,采用降水集中指数(PCI)和降水集中度(Q),通过ArcGIS的Kriging空间插值方法,研究全省1956—2021年的降水年内时间分布及降水集中度年际变化特征,探求多流域聚集地区降水时间分布的时空分异规律,为水资源调配和水旱灾害防御提供技术支撑。
1 研究区域、数据与方法
1.1 研究区域
河南省地处中原,地势西高东低,占地面积约16.7万km2,其中海河流域面积约1.53万km2,约占全省总面积的9.1%;黄河流域面积约3.62万km2,约占全省总面积的21.7%;淮河流域面积约8.64万km2,约占全省总面积的52.9%;长江流域面积约2.76万km2,约占全省总面积的17.6%。全省地貌大致由豫北、豫西、豫南山地和黄淮海平原、南阳盆地组成。全省属于暖温带-亚热带、湿润-半湿润季风气候,具有明显的过渡性气候特征。受季风气候的影响,全省南北气候差异大,南部呈湿润半湿润特征,北部呈半湿润半干旱特征[19]。
河南省多年平均降水量768.5 mm,受大气环流和复杂地形的影响,全省降水量等值线整体呈东西走向,平原区呈东北-西南走向,伏牛山东麓一带、大别山区北侧新县一带、太行山东麓卫辉市一带,是降水量高值区。全省降水主要集中在汛期(6—9月),春、秋、冬3季多干旱少雨,多年平均汛期降水量占全年降水量的60%以上,最大年降水量与最小年降水量比为2.3。全省降水量年内分配不均、年际变幅较大,局部地区容易产生水旱灾害。
1.2 研究数据
研究采用全省范围内水文部门522个雨量站点的整编数据(海河流域269站/km2,黄河流域340站/km2,淮河流域300站/km2,长江流域383站/km2),时间长度为1956—2021年。站点情况见图1和表1。

表1 各流域站点数量 个
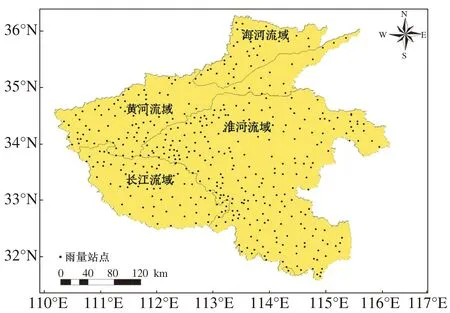
图1 全省雨量站点分布和流域划分
所用绝大部分站点资料完整、连续,个别站建站年份晚于1956年,借用临近站点数据对其建站之前年份的降水量数据进行插补。
1.3 研究方法
1)降水集中指数(PCI)。降水集中指数(PCI)计算方法由DE LUIS M等[20]提出,是对OLIVER J E[21]所定义的PCI的改进,其定义如下:
(1)
式中:xi为第i个时段的降水量,mm;N为时段数。
由式(1)可知:若年降水量都集中在一个时间段内,则PCI的值为100,最高;若年降水量均匀分配于N个时间段,则PCI值为1/N。在实际应用中,若以月为时间尺度,国际普遍认为:当PCI≤10时,表示降水时间分布较均匀;当11≤PCI<20时,表示降水时间分布偏集中;当PCI≥20时,表明降水时间分布异常集中。
2)降水集中度(Q)。根据统计学理论,信息熵用于描述离散随机事件的出现概率,当随机事件的不确定性增大时,信息熵的数值也随之增大。因气候变量可视为随机变量,基于信息熵理论,王睆等[17]和LI H等[22]以降水量为随机事件,定义降水集中度Q为:
(2)
(3)
式中P(xi)为xi对总降水量的贡献率。
由式(2)可知:降水集中度Q值介于0和1之间;如果全部降水都集中在一个时次,则Q=1;如果降水均匀分布在每一个时次,Q=0。即当降水时间分布较集中时,该值较大;当降水时间分布较均匀时,该值较小。
3)标准化降水指数(SPI)和气象干焊表征指标Z。为研究降水分布特征与降水丰沛程度的关系,需要用到SPI和Z。其中,SPI是MCKEE T B等[23]为评估气象干旱状况而提出的标准化指标,其原理是认为降水量概率密度函数服从Γ分布,通过降水量概率密度函数求解累积概率,再将累积概率标准化求得SPI值,具体计算如下:
(4)
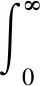
(5)
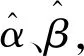
(6)
(7)
式中n为系列长度。
一定时间尺度的累积概率为:
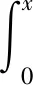
(8)
式中q是降水量为0的累积概率。H(x)可以通过下式转换为标准正态分布函数:
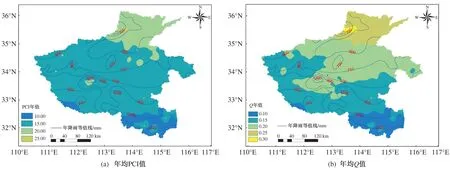
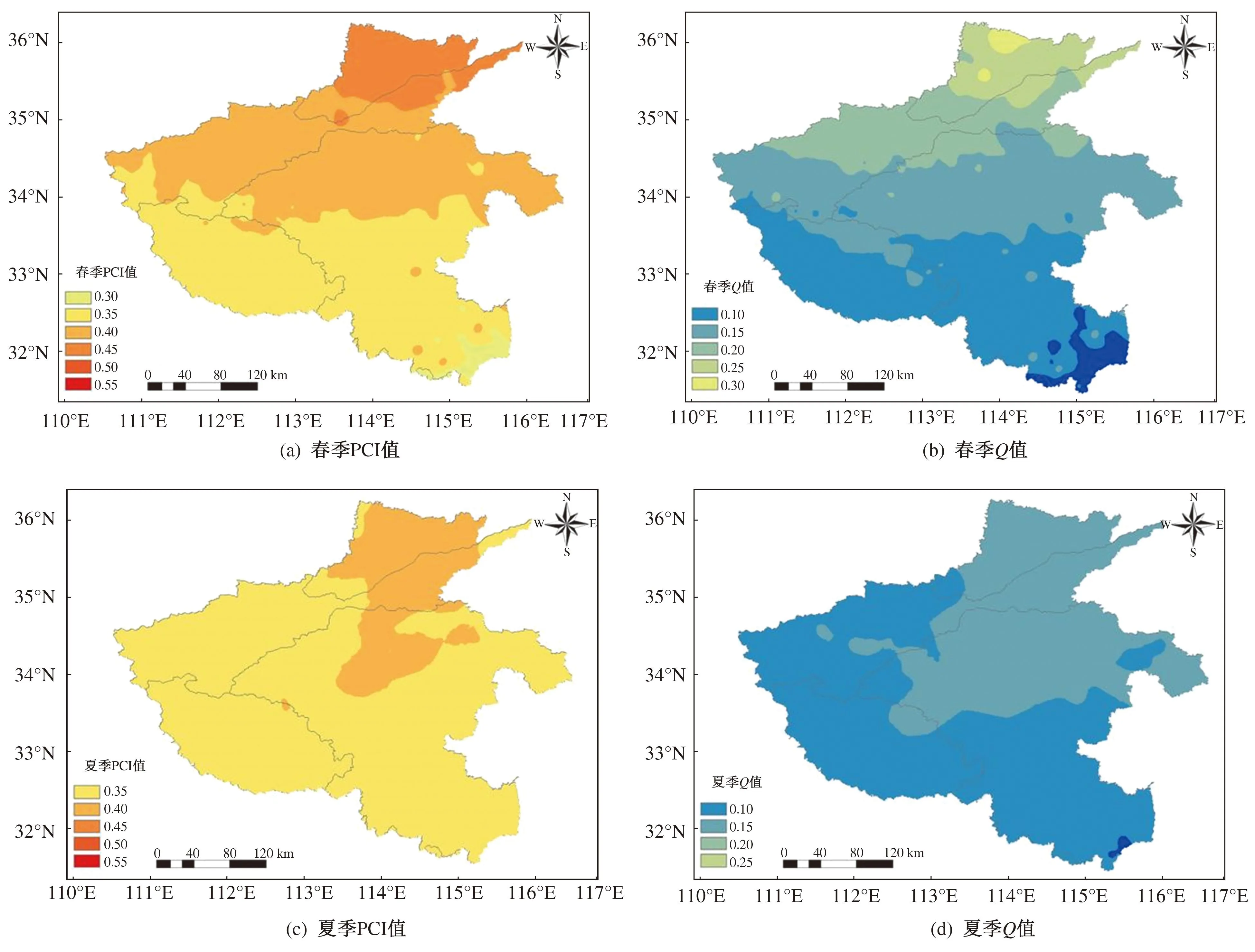
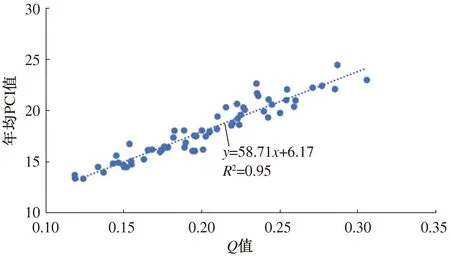
当0 (9) (10) 当0.5 (11) (12) 式中c0、c1、c2、d1、d2、d3为系数,其中c0=2.515 517、c1=0.802 853、c2=0.010 328、d1=1.432 788、d2=0.189 269、d3=0.001 308。 Z是国际上广泛应用的气象干旱表征指标。假设降水量服从P-Ⅲ型分布,通过对降水量进行正态化处理,可将其概率密度函数进行转换运算,进而计算Z[24]: (13) 式中:Cs为偏态系数;φi为标准变量。 根据SPI和Z值划分7个旱涝等级,各等级对应的指标见表2。 表2 旱涝等级及对应的SPI和Z值 基于雨量站点系列数据,采用式(1)和式(2)计算各站的降水集中指数PCI和降水集中度Q(为便于分析,文中涉及PCI和Q值的所有图为示意图,采取图例中所示值为近似值,以同种颜色显示),并基于ArcGIS软件,采用Kriging方法进行空间插值,将1956—2021年多年平均年值情况绘于图2,并在图2上叠加河南省降水量多年均值等值线。 图2 多年平均PCI值、Q值的空间分布 1) 1956—2021年河南省多年平均PCI值为13.34~24.45,平均为17.98;多年平均Q值为0.11~0.31,平均为0.20。多年平均PCI值和Q值的空间分布总体呈现由北向南递减的特点,河南省北部降水时间分布较集中,南部降水时间分布较均匀。 2) 降水集中度的高值区位于海河流域卫河支流峪河、石门河上游、新乡卫辉市太行山东麓,同时卫辉市太行山东麓是全省三个降水量高值区之一,该区域多年平均降水量较河南省海河流域多年均值多49%,同时表现出北方地区年降水日数少的普遍特点,但由于地形原因降水量明显多于周边区域,降水集中度较高。 3) 降水集中度低值区主要位于淮河干流以南的信阳市境内除去史灌河、泼河以及寨河和竹竿河上游的大部分地区,竹竿河上游大部分地区是全省降水量丰沛区,年均降水量达1 000 mm以上,年均降水日数达116 d。 4) 淮河流域南部PCI值和Q年值较低,极端旱涝事件发生风险相对较小;海河流域和黄河流域东部区域的PCI值和Q值较高,降水时间分布较为集中,极端旱涝事件发生风险较大。 以上结果总体上与段亚雯等[11]、刘向培等[13]在全国尺度上的研究结论基本一致。 以年均PCI值和Q值随时间的总体变化率来表征变化趋势,取PCI和Q值时间序列拟合直线的斜率作为变化趋势,将其空间分布情况绘于图3。 从图3可以看出: 1) 1956—2021年河南省年均PCI值和Q值的变化趋势较小,量级一般为10-3。 2) 从全省范围看,大部分区域年均PCI值和Q值略有增加,即降水时间分布略趋于集中,变化趋势总体呈现北部降低、南部升高的趋势。 3) 从省内不同流域看,海河流域大部分区域、黄河流域的中部和东部区域,以及淮河流域的西北区域降水时间分布略趋于均匀,其他区域降水时间分布略有集中的趋势。 基于雨量站点系列数据,计算各站的降水集中指数(PCI)和降水集中度(Q),以当年3—5月、6—8月、9—11月、当年12月—翌年2月分别作为当年春季、夏季、秋季、冬季。将1956—2021年多年平均季值绘于图4。由图4可知:冬季的PCI和Q值最大,远超过其他季节的,说明冬季降水时间分布最集中,而夏季的降水时间分布相对其他季节而言最均匀,春季和秋季居中。 图4 PCI季值、Q季值多年平均空间分布 4个季节中,冬季PCI值和Q值最高的原因主要是:河南省属亚热带向暖温带过渡的大陆性季风气候,四季分明、雨热同期,冬季降水量较少,很多年份甚至整个冬季无有效降水,从而导致冬季降水集中程度最高,这在河南省内的海河流域最为显著。 从全省范围内的空间对比来看,降水时间分布集中程度呈现由北向南递减、由西向东增加的特点,且冬季的区域间差异最大,而夏季的区域间差异最小。主要原因是:河南省具有自东北向西南由平原向丘陵山地气候过渡的特征;冬季降水多为局部发生且量级小,这也导致降水时间均匀性差异较大,这在河南省内的黄河流域最为明显。 以PCI和Q的季值随时间变化的总体变化率表征降水变化趋势,PCI和Q变化趋势类似,以Q值为基准,列出Q值变化趋势图,如图5所示。 图5 Q值变化趋势空间分布 由图5可知: 1) 降水分布随时间的变化趋势不明显,量级一般为10-3,总体变化为-0.002~0.005,但季节性差异较大,其中夏季降水集中程度变化较冬季的偏小,表明气候变化影响下极端旱涝对冬季的影响要大于夏季的。 2) 针对空间分布而言,夏季变化趋势空间差异性较小,省内大部分区域略趋于均匀,海河流域部分区域、黄河流域中部和豫东平原大部分的降水时间分布趋于集中,其他季节变化趋势空间差异性较大,尤其是冬季。在进行变化趋势显著性检验中发现:信阳市西南部及南阳盆地的小部分区域夏季降水量集中度减小趋势通过了90%的显著性检验;开封市中部区域冬季降水量集中度增加趋势通过了90%的显著性检验,说明部分区域降水集中程度变化显著。 从PCI和Q多年平均空间分布和变化趋势看,二者具有极强的相关关系,为进一步定量验证,将二者绘制于图6。 图6 年均PCI值与Q值相关性 由图6可知,PCI值与Q值具有极好的相关性,线性相关系数达到0.95。为探究降水时间分布与降水量及气象干旱的相关性,采用式(6)~式(9)计算SPI和Z值,进一步研究年平均Q值、年降水量、年均Z值的相关关系,见表3。 表3 降水集中度Q(yQ)与年降水量、干旱指数SPI、干旱指数Z之间的相关性分析表 从表3可以看出,Q值与年降水量、SPI值和Z值等单变量间有一定的正向关联性但相关性极弱,表明降水时间分布虽然具有随着降水量或者气象干旱程度的增加而偏集中的可能,但与单个变量的相关性较弱,相关系数不到0.2。Q年值与年降水量、SPI值和Z值3个单变量有一定的正向关联性,相关性强于单个变量,但总体而言相关性仍不强,相关系数不到0.3。为进一步分析Q值与年降水量、SPI值和Z值之间的相关性,除线性回归公式以外,还拟合了指数函数、幂函数、对数函数、多项式、滑动平均等多种形式的公式,结果发现相关系数均在0.3以内,相关性较弱。由此说明,降水时间均匀特征与降水量、干旱指数有定性的关联,但没有显著的相关性。实际上,借鉴历史实测资料也可以发现,降水量大的年份,降水集中度(PCI)与Q值不一定高,降水集中度还与连续降水天数、日降水量等有关,正如1960年和1989年,河南省年降水量分别为725.3 mm和813.2 mm,虽属平水年(河南省多年平均降水量768.5 mm),但都发生了全省范围内的旱情[25]。因此,在关注旱涝事件过程中,不可只关注降水量和气象干旱程度,还应该兼顾降水时间分布特性。 以河南省为研究对象,基于多站点长系列降水数据,采用降水集中指数(PCI)和降水集中度Q等指标,分析了全省降水时间均匀特征及变化特点。取得的主要结论如下: 1) 河南省降水时间均匀特征具有地区差异性,北部降水时间分布较为集中,南部较为均匀,集中程度总体呈现由北向南递减的特点。省内海河流域和黄河流域东部区域降雨时间分布较为集中,极端旱涝事件发生风险较大,长江流域西南部和淮河流域东南部区域降雨时间分布相对较为均匀。从季节尺度上来看,冬季的降水时间分布最为集中,夏季的降水时间分布最为均匀,春季和秋季居中。 2) 河南省降水时间均匀特征变化趋势总体较小,省内海河流域大部分区域、黄河流域中、东部区域以及淮河流域的西北区域降水时间分布略趋于均匀,其他区域略趋于集中;从季节尺度上来看,夏季降水集中程度总体略减小且变化趋势空间差异性较小,冬季的略增大且空间差异性较大。 3) 降水时间均匀特征与降水量、气象干旱程度有一定的正向关联性但相关性极弱,表明降水时间分布集中程度虽具有随着降水量或者气象干旱程度增加而偏集中的可能,但仍需要将降水时间均匀特征作为一个独立因素进行考虑。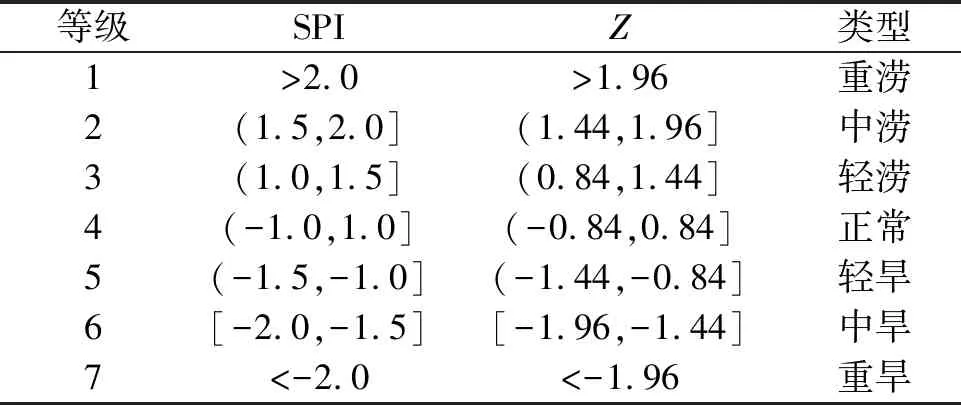
2 年降水时间均匀特征和变化趋势
3 季降水时间均匀特征和变化趋势
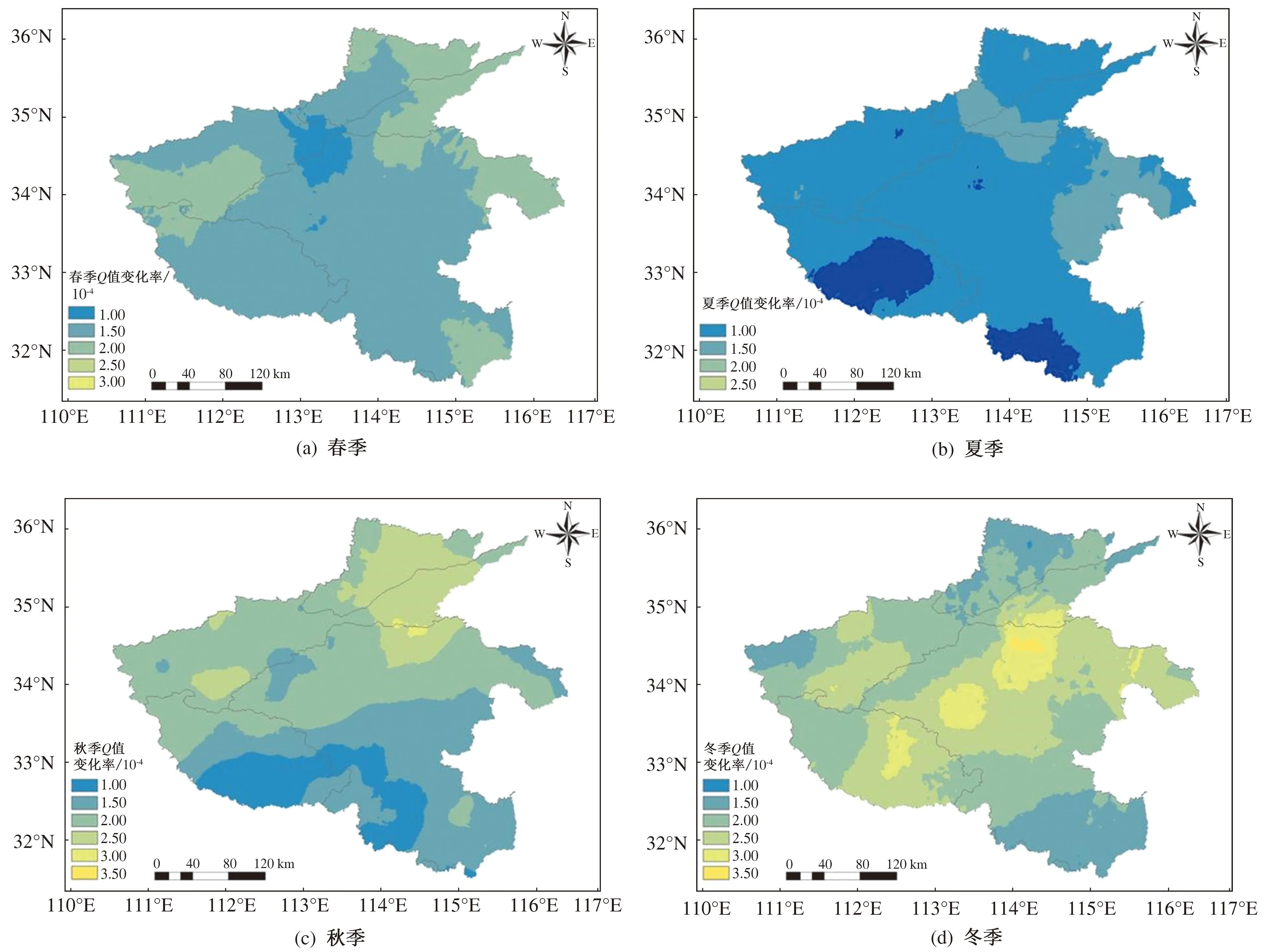
4 降水时间均匀特征与降水量、干旱指数SPI和Z之间的关系

5 结论
