抽水蓄能电站地下厂房通风数据模拟研究

中国水电四局第三分局 郑 凯 潘润霞

1 抽水蓄能电站地下厂房自然通风的影响因素

抽水蓄能电站地下厂房自然通风的影响因素主要有风压与热压两大因素：一是风压。各洞口与竖井顶部排风口受到的风压作用较大，其压力大小主要取决于室外风速与风向。根据相关学者的研究，若风速处于1～9m/s，且风向与风口平面相垂直时，此时风压系数可取值为0.7，则对应的风压Pw计算表达式如下所示：

式中，ρw、uw分别为室外空气密度与风速，单位分别为kg/m3与m/s；cosα 为当室外风向与洞口平面间夹角为α 时的余弦值。

二是热压。热压是指抽水蓄能电站地下厂房因为温差而引起的室内外空气压力差，一般而言，交通洞与出线竖井的两端高差较大，当室外空气流入到地下厂房后，会同厂房内的岩壁以及散热设备间发生换热现象，从而导致通风状态下的地下厂房具有一定热压[1]。热压并非独立的因素，其既取决于气流温度或密度分布的通风结果，又受到通风流动的动力与传热效果等影响，表现出较强的动态变化特性[2]。

地下厂房自然通风各参数为风压与热压相互作用的结果，具体相互关系如图1所示，若想准确预测出地下厂房通风数据，则必须将风压与热压对自然通风的影响关系用数学模型表示出来，即需要构建通风流动与维护结构动态传热的计算模型。

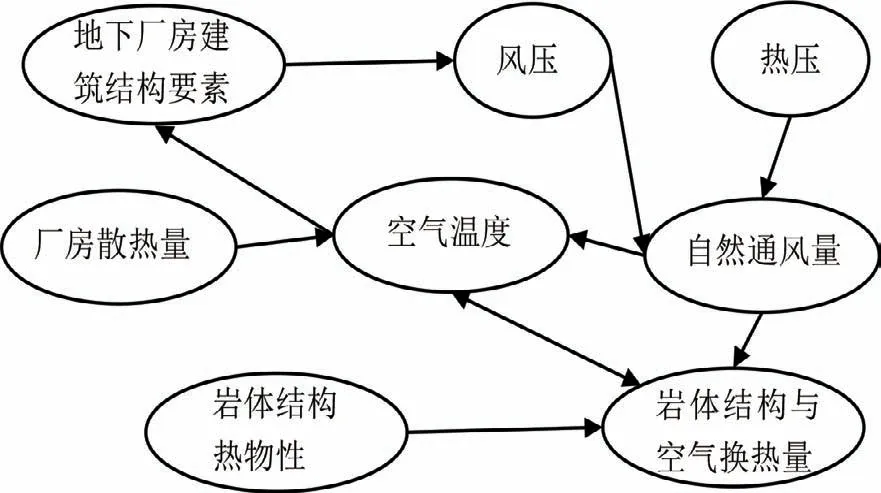
图1 地下厂房自然通风的作用关系

2 抽水蓄能电站地下厂房通风计算模型

2.1 各洞室温度分布计算方法

在模拟地下厂房通风数据时，需要考虑各洞室的总散热量，以确定精准的通风热压值，散热量逐时值Qe的计算表达式如下：

式中，Q 为设备固定散热量，单位为kW ；Qp为随工况变化下的发电机组满负荷状态时的设备散热量；η 为随工况变化的设备逐时散热率。

从开始侍酒师考试，到摘取侍酒师大师桂冠，这一路，他走了十年，谈起当初父母并不同意他转换专业去学葡萄酒，他觉得父母除了不了解这个行业以外，更多是不希望他轻易放弃，但他却轻描淡写地感慨了一句：“我做的最正确的一个决定，就是去学葡萄酒。”

按照洞室结构特征，可将不同洞室分为两类，一类为交通洞、排风竖井等长隧道式洞室，另一类为主机洞等功能层洞室，针对两类洞室需要采用对应的网格划分方法进行空气参数分布求解[3]。长隧道式洞室可按照气流流动方向进行空气域划分，形成多个轴向长度为Δz 的分支，根据空气温度沿程变化可准确计算出热压。则空气流过分支的流动阻力ΔP 表达式如下：

式中，K 为流动通道的平均避免粗糙度，单位为m；de为分支传热当量直径，单位为m；l 为分支长度，单位为m；ξ 为局部阻力系数；M 为分支内的通风量，单位为kg/s；F 为分支截面面积，单位为m2。并且，分支热压由内部的温度分布决定，表达式如下：

式中，dz 为微远段的高程增量，单位为m；Tw为室外空气的热力学温度，单位为K；T 为分支内部微元段上空气的热力学温度。当温度处于线性分布状态下，分支热压的计算表达式调整如下：

式中，Ts、Te分别为流入、流出分支的气流质量平均热力学温度。

功能层洞室的体积较小，且送、排风口间的高差较小，因此洞室内的热压动力较小，可忽略不计，只需要将其整体视为一个网格，计算出洞室内的空气参数与岩壁传热量[4]。在计算热压值时均需要根据实际情况合理添加热源项，表达式如下：

2.2 通风流动计算模型

地下厂房的自然通风形成由动力及其对应阻力的平衡状态决定，分支节点处的空气流动在质量流量上处于平衡状态，存在如下表达式：

式中，aij为符号数，根据节点归属与的流入流出情况Mj进行定义，当节点为分支端点时，可将Mj流入时的aij定义为-1，而流出时的aij定义为1，而节点并非分支端点时，aij定义为0；m 为节点数-1；n 为分支数。

当数个分支构成闭合回路时，同样需要保持压力平衡状态，此时气流沿回路方向形成的流动动力与阻力的代数和为0，表达式如下：

式中，cij为符号数，根据分支在回路中流向进行定义，当与回路同向时为1，异向时为-1，分支不属于i 回路时为0。

抽水蓄能电站的风压可根据式（8）计算，室外风速可取地区各季节室外风速的平均值，根据风压方向与通风方向的关系，当二者相同时“±”取“+”，不相同时取“-”。

2.3 围护结构传热计算模型

地下厂房在通风热交换中的空气温度tn（τ）会与围护结构产生相互作用，因此有必要计算此部分的传热情况。为本次计算中使用Z 传递系法对空气温度进行测算，室外空气温度的变化规律等同于年周期频率温度波与日周期频率温度波之和，在不同温度波作用下，仍然需要考虑到围护结构厚度的差异。因此需要进行分别计算，其中分支内空气温度的逐时值tkl为：

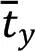
考虑到线性系统的叠加原理特征，围护结构的逐时传热量qij的组成如下：

3 模型数值求解

3.1 地下厂房通风分类

考虑到对自然通风量的控制情况，可将抽水蓄能电站的通风方案分为两种不同的情况：一种为已知地下厂房各个洞室结构、设备散热量与实际变化规律和岩体热物性等条件，计算分析仅依靠自然通风动力下的实际通风情况。该情况下不会采用启停风机、调节风阀开度等，仅依靠自然通风动力，而考虑到自然通风中风量会实时发生变化，因此可确定该情况为通风量不受控制的自然通风。

另一种为已知地下厂房各个洞室结构、设备散热量与实际变化规律和岩体热物性等条件，借助通风控制方式，将通风量控制在某一目标值附近。该情况需要计算自然通风量情况，以保证通风量在确定值条件下，进行合理有效的通风控制，按照地下厂房室内通风需求进行定量通风，因此可确定该情况为按需通风。

3.2 不受控条件下的通风数值计算

抽水蓄能电站地下厂房的通风量在不受控条件下，由自然通风动力决定，在通风数值计算中采用岩体能量嵌套模型方程的耦合方式进行计算求解。该条件下虚假岩体传热量q，并利用自然通风计算模型、通风流动模型与通风传热传质模型完成对通风量G 的迭代计算。由此可获得通风量G 每次迭代的修正值：

在通风量不受控制时，采用Z 传递函数法计算岩壁传热是，认为传热量为两个不同频率温度波作用下传热量的叠加值，因此在对通风传热传质应用中需要分为两个不同的时间层次子模型，在计算抽水蓄能电站地下厂房自然通风逐时，变化规律时应先计算以天为时间的自然通风日均变化参数实际变化情况。

3.3 按需通风条件下的通风数值计算

按需通风条件下，各个通风洞室内的风量与风速数值已知，对于结构尺寸已经确定的抽水蓄能电站地下厂房，可计算确定其通风流动路径的总抗阻值S。在确定通风量G 与热压Pr后，可获得抽水蓄能电站地下厂房的通风总动力需求值：

式中，P 为通风总动力需求值；Pw为风压；Pj为超静压差；Pf为热压。

在通风设计中，当自然通风动力小于时，应通过引入风机压力满足通风总动力需求，其中所需的风机压力值为：

当自然通风动力大于P 时，表明自然通风动力已经能够满足通风总动力需求，因此需要增加通风路径的抗阻，提高通风阻力。在抽水蓄能电站地下厂房中增加通风路径抗阻须对其数值进行计算，计算方法如下：

式中，ΔS 为通风路径阻抗增加值。

设计中，通风路径质量阻抗增加值是指开启空气幕或减小风阀开度的定量值，在地下厂房中增加通风路径阻抗后，通风总动力的需求值与自然通风动力之间的平衡关系为：

式中，ΔP 通风路径阻抗增加值所导致的通风阻力增量。

通过上式可计算出不同时刻条件下按需通风控制措施情况，从而保证地下厂房的通风量在各个时段能够与需求量保持一致。

本文主要研究了抽水蓄能电站地下厂房通风计算方法，分析了电站的基本工况与相关设备的启停变化规律，结合实际情况进行了通风方案分类处理。其中，发现抽水蓄能电站的自然通风的主要影响因素为热压与风压，在考虑室外风压与实际运行工况条件下，对通风网络模型进行了优化处理，并给出了相应数值计算求解方法，研究发现全年逐日变化会对通风控制产生比较明显的影响，因此在通风控制中要对此进行重点分析，以此为抽水蓄能电站地下厂房通风模拟计算提供有效参考。