考虑短路故障影响含风电电力系统恢复决策优化方法研究

国华（利津）新能源有限公司 曹善旭

1 建模风能系统在短路事件影响下的恢复策略

1.1 短路电压与节点阻抗之间的相互作用

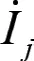
此外，对于线路p-q 上发生的三相短路故障，本研究考虑了线路p-q 的阻抗，并引入了p 点到短路点的距离表示。基于电网理论和原网络的阻抗矩阵，导出了故障点f 与网络中其他节点i 的互阻抗，以及故障点f 的自阻抗的关系式。

1.2 风电系统低压穿越故障分析与脱网预测模型

该模型不仅用于判断特定故障情况下风电系统是否脱网，还可用于量化分析短路故障对系统恢复的影响。结合风电脱网情况、系统的源网状态及潮流分布，本模型为评估和优化风电系统在低压穿越失败情况下的应对策略提供了一个全面的分析框架。

1.3 统一建模短路故障前后的影响

基于风电脱网判断模型和直流潮流模型，本研究构建了短路故障切除前系统的失负荷风险模型，包括功率流动约束、节点功率平衡、发电机输出限制、风电输出限制、负载需求限制等方面的计算。模型还考虑了短路故障切除后的断线影响，提出了相应的失负荷风险模型，涵盖了功率流动和线路容量约束、节点功率平衡、发电机输出限制、风电站输出限制、节点负载需求限制等方面。

2 系统恢复期间的电源特性建模

2.1 考虑风电出力预测误差及波动性的风电并网时机约束

2.1.1 基于Wasserstein 距离的极限预测误差估计

为保证恢复方案鲁棒性，采用基于Wasserstein距离的方法估计风电出力极限预测误差，此法通过历史数据分析建立误差模糊集，确定风电出力误差上限。考虑机组调节能力和最大频率偏差，制定考虑预测误差的风电并网时机约束，如公式（1）所示：

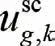
2.1.2 负荷持续性恢复下的风电并网时机

为了避免已恢复负荷由于风电出力波动而再次停电，需要考虑风电出力的预期变化幅度和系统机组的功率调节能力。设定风电在n 个时段的预测出力，并计算各时段间的出力变化。以最大正数变化作为极限波动出力，可以得到负荷持续恢复下的风电并网时机约束：

公式（1）和公式（2）共同构成了考虑风电波动性和预测误差的并网时机约束。

2.2 非固定恢复时段的机组灵活启动模型

在系统恢复决策中，非黑启动机组的启动顺序对于整体恢复效率至关重要。本研究提出了灵活爬坡模型，允许机组在达到稳燃出力后自由调节出力。为实现模型的线性化表达并嵌入求解，构建了非固定恢复时段的机组灵活启动决策模型。公式（3）和公式（4）是该模型的核心：

机组启动状态与启动时间的关系：

发电机的运行状态与时间的关系：

除此之外，模型还包含了发电机的稳定运行状态、功率输出和频率支持功率的限制，确保机组在特定状态下的稳定运行。为确保机组启动与网架重构的互动，模型还设定了机组启动与网架重构间的联系，以及对机组启动功率和总发电能力的约束。通过这些综合措施，模型确保了恢复过程中的效率和安全性，同时提高了系统恢复方案的灵活性和适应性。

3 考虑短路故障影响的含风电电力系统恢复决策优化模型

3.1 基于滚动窗口优化目标动态更新的系统恢复框架

在含风电的系统中，传统的三阶段恢复模式可能不再适用。本文提出的基于滚动窗口优化目标动态更新的恢复框架旨在实现恢复决策与恢复模式的动态协调。该框架包含以下四项恢复目标：

系统发电能力最大化：

系统负荷恢复最大化：

网架恢复规模最大化：

短路故障影响最小化：

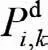
其次，基于四个恢复目标，提出三种恢复模式S1、S2、S3，每种模式有关联的恢复目标权重w1、w2、w3、w4。模式S1中，w1和w4为1，w2和w3为0，优先考虑特定目标。模式S2中，w2、w3和w4为1，w1为0，反映不同的优先级。模式S3中，w3和w4为1，w1和w2为0，表明恢复目标的优先顺序不同，以适应特定恢复需求和策略：maxf=w1fGen+w2fLoad+w3fNet+w4fRisk。

式中：w1、w2、w3、w4分别代表与发电性能、负载满足、网络效率和风险管理相关的权重系数；fGen代表发电优化目标函数的值，关注于最大化发电效率和产量；fLoad代表负载优化目标函数的值，关注于最大化负载需求的满足；fNet代表网络优化目标函数的值，关注于电力网络的运行效率；fRisk代表风险优化目标函数的值，关注于降低系统运行风险。

最后，使用基于滚动窗口的系统恢复框架，该框架动态更新优化目标。在该框架中，每个时段的恢复决策执行后，系统会根据当前恢复情况判断是否需要切换恢复模式。该方法实现了恢复决策与恢复模式之间的动态协调。

3.2 网络潮流及拓扑约束

在基于滚动窗口的系统恢复框架中，动态更新优化目标，确保恢复决策与恢复模式之间的协调。核心公式之一是线路的有功和无功潮流表达式，关键地反映了线路投运状态下的电力流动情况：

此外，模型包括节点的有功和无功平衡方程，确保在每个时段每个节点上电力的供需平衡。还设定了节点电压的最小和最大限制，以及线路状态变量的约束，这些保证了电网的稳定性和安全运行。对网架拓扑的约束包括节点与线路状态的映射关系，以及线路最大投运数的限制，确保网架在恢复过程中的连通性和流量的可行性。

优化目标是在满足所有这些约束条件下，找到最佳的电力系统运营策略。该模型综合了节点阻抗线性建模、短路故障影响、风电并网时机、机组启动优化以及网络潮流和拓扑约束，全面考虑了电网在各种运行条件下的稳定性、安全性和经济性，同时也考虑了系统的可靠性和环境影响。

3.3 模型整体求解流程

该模型的整体求解流程是基于滚动优化策略的。首先读取停电前系统状态和元件参数，设定初始恢复目标函数和时段。然后求解恢复决策优化模型，得到优化决策窗口内的各时段恢复方案。如果方案校核通过，则执行该时段的恢复方案，否则重新进行模型求解。

若系统内的机组、负荷及网架均已完成恢复，则结束求解。反之，则需要更新机组、网架和负荷状态，根据恢复情况切换恢复模式、更新模型结构和恢复决策窗口。同时，生成短路故障场景集和故障切除后的断线故障场景集，用于下一次优化求解，重复此流程直至系统完全恢复。

4 算例分析及效果评估

4.1 系统恢复效率的对比分析

系统恢复效率的关键在于缩短停电时长和减少负荷损失，IEEE-39和IEEE-118系统的数据分析显示（如图1所示），风电参与可显著缩短恢复时间和减少负荷损失，特别在IEEE-118系统中恢复时间提前两个时段。方案M4与M3相比，负荷恢复效果较差，凸显动态更新恢复目标的重要性。

在网架恢复方面，IEEE-39系统第9时段进入S3阶段全面负荷恢复，而IEEE-118系统第19时段完成后进行网架全面恢复。机组恢复方面，各机组快速启动、稳定运行，不同方案下机组启动顺序有异，但系统内机组出力持续增长以加快负荷恢复。模型求解效率方面，IEEE-39系统M3方案总用时68.797s，平均每窗口耗时3.276s；IEEE-118系统M3方案总用时603.750s，平均每窗口耗时25.156s。MILP 模型求解Gap 值低于0.05%，M4方案求解用时高于M3，突显动态调整恢复目标和模型结构的必要性。

4.2 系统恢复过程中短路故障风险的对比分析

对于恢复过程中的短路故障影响，以故障场景下的失负荷量为基础对比M2和M3方案下的短路故障风险。其中，方案M2、方案M3、方案M4故障前/后总失负荷量（单位100MW）分别为：70.398/250.598、1.298/3.489、13.360/45.542。 结果表明，M3方案在考虑恢复过程中的短路风险后能有效降低风险。如在IEEE-39系统中，M3方案的短路故障风险比M2方案显著降低。

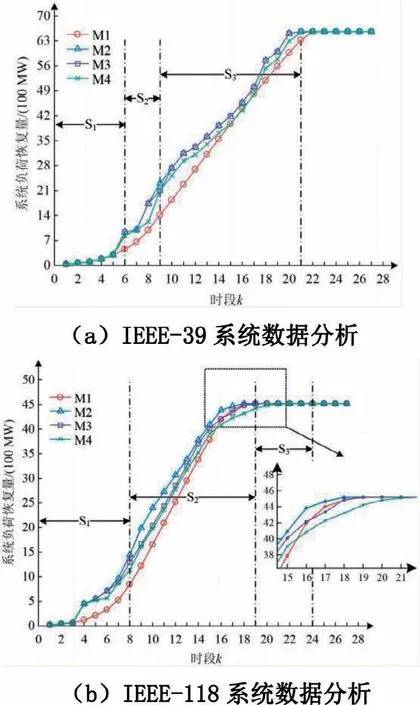
图1 EEE-39和IEEE-118系统的数据分析

在IEEE-118系统中，由于网架规模较大且机组数量较多，M3方案可通过调整线路投运次序和源网恢复状态来降低短路故障风险。M3方案将短路故障风险显著降低，而M4方案由于未能有效协调恢复目标与恢复工况，短路故障风险优化效果较差。考虑短路故障影响的含风电电力系统恢复策略不仅提升了系统恢复效率，还有效降低了恢复过程中的短路故障风险，从而提高了系统恢复方案的安全性。