基于改进黏菌算法的综合能源系统优化调度
2024-03-07张壮杰
张壮杰, 黄 伟
(上海电力大学 自动化工程学院, 上海 200090)
随着全球经济快速发展,能源短缺与环境污染问题愈发严重。综合能源系统(Integrated Energy System,IES)能够多梯级利用能源,可以促进可再生能源消纳,是实现节能减排的有效途径,可推动实现我国提出的“双碳”目标[1-4]。
目前,关于IES模型已有大量的相关研究。文献[5]建立了结合可再生能源以及储能装置的IES模型,文献[6]建立了工业园区低碳经济运行的IES模型。但上述研究只建立了供能侧的模型,未考虑到用能侧的优化。针对这一问题,文献[7]考虑了针对电力系统的电负荷需求响应;文献[8]引入价格弹性矩阵描述需求响应行为,并分析了其有效性;文献[9]引入可转移负荷对负荷侧用能进行优化。但上述研究未考虑不同负荷响应特性的情况。
IES优化调度模型具有大规模、非线性、非凸的特点。文献[10-11]采用粒子群优化(Particle Swarm Optimization,PSO)算法以及改进PSO算法优化IES模型,但PSO算法搜索速度较慢,精度不高,易陷入局部最优。文献[12-13]提出用灰狼优化(Grey Wolf Optimizer,GWO)算法求解IES优化调度问题,算法性能明显提升,但搜索速度仍有待提高。文献[14]采用麻雀搜索算法(Sparrow Search Algorithm,SSA)对IES优化调度问题进行求解,搜索速度快,但初始最优解较差,算法性能仍有待提升。
综上所述,本文建立计及综合需求响应(Integrated Demand Response,IDR)的IES优化调度模型,提出了一种改进的黏菌优化算法(Slime Mould Algorithm,SMA),求解IES优化调度问题,并结合算例进行仿真验证,为IES的实际调度运行问题的求解提供参考。
1 系统建模
1.1 IES模型
IES架构如图1所示。

图1 IES架构
从能量平衡角度,建立图1中各设备数学模型如下。
燃气轮机(Gas Turbine,GT)模型为
(1)
式中:PGT.e,PGT.g,PGT.h——GT发电功率、耗气功率、产热功率;
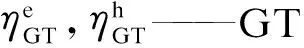
余热锅炉(Waste Heat Boiler,WHB)模型为
(2)
式中:PWHB——WHB输出功率;
ηWHB——WHB产热效率。
燃气锅炉(Gas Boiler,GB)模型为
(3)
式中:PGB.h,PGB.g——GB产热功率、耗气功率;

电热锅炉(Electric Boiler,EB)模型为
(4)
式中:PEB.h,PEB——EB产热功率、消耗电功率;

电制冷机(Electric Chiller,EC)模型为
(5)
式中:PEC.c,PEC——EC输出制冷功率、输入电功率;

吸收式制冷机(Absorption Chiller,AC)模型为
(6)
式中:PAC.c,PAC——AC制冷功率、输入热功率;

风力发电机(Wind Turbine,WT)模型为
(7)

v,vin,vr,vout——实际风速、启动风速、额定风速、切出风速;
K——出力特性系数。
光伏(Photovoltaic,PV)模块模型为
(8)
式中:PPV,Pn,PV——光伏模块输出功率、额定输出功率;
fPV——能源转换效率;
It,Is——t时刻辐射强度、标准辐射强度;
εp——温度功率系数;

储电装置(Electric Storage,ES)模型为
(9)

μe——ES自放电率;

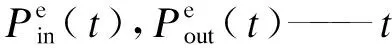
1.2 需求响应模型
在负荷侧通过引导用户主动改变原有用能需求及习惯,从而改善源荷两侧供需的不平衡关系,提高系统运行经济性。根据负荷响应特性,需求响应可分为价格型需求响应和替代型需求响应[15]。
价格型需求响应模型为
(10)

Em——弹性系数;

替代型需求响应模型为
(11)
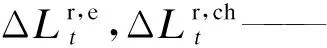
εe,h——电热替代系数;
ve,vh——电能和热能的单位热值;
φe,φh——电能和热能的能源利用率。
2 目标函数与约束条件
2.1 目标函数
目标函数分为以IES在运行过程中运行成本最小为目标和碳排放成本最小为目标两种。
2.1.1 运行成本
IES运行成本Ch包括购电成本Ce、购气成本Cg以及系统运维成本Cop。
Ch=Ce+Cg+Cop
(12)
购电成本Ce为
(13)
式中:T——运行周期时长;
cb,t,cs,t——t时刻购、售电电价;
Pb,t,Ps,t——t时刻向上级电网购、售电功率。
购气成本Cg为
(14)
式中:cg——购买天然气单价;
Pg,t——t时刻购买天然气功率。
系统运维成本Cop为
(15)
式中:i——IES设备,i=1,2,3,…9分别表示GT,WHB,GB,EB,EC,AC,WT,PV,ES;
ωi——设备i的运维系数;
Pi,t——t时刻设备i的输出功率。
2.1.2 碳排放成本
(16)
式中:CH——碳排放成本;
W——惩罚系数,包括排放惩罚和环境价值;
μe——单位电功率对应的CO2排放系数;
μf——单位体积天然气对应的CO2排放系数。
2.2 约束条件
设备功率约束条件为
(17)
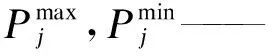

电、热、冷能功率平衡约束条件为
(18)
式中:Le,Lh,Lc——系统的电、热、冷负荷量。
3 算法介绍
3.1 SMA
SMA通过模拟黏菌捕食实现智能寻优功能。黏菌在觅食过程中的位置变化如下:
(19)
式中:X(k+1)——迭代第k+1次时更新后的黏菌位置;
r1——随机数;
UB,LB——搜索边界上下限;
z——常数,取0.03;
Xb(k)——迭代第k次时黏菌最优个体位置;
vb,vc——随机数,vb∈[-a,a],vc∈[0,1];
W——黏菌重量;
XA(k),XB(k)——迭代第k次时随机选择的黏菌个体位置;
X(k)——迭代第k次时黏菌位置。
p和a的公式如下:
(20)
式中:S——当前黏菌个体的适应度;
DF——迭代过程中最佳适应度;
kmax——最大迭代次数。
3.2 改进SMA
SMA初始化种群时,为了增强种群多样性,将混沌映射与反向学习相结合,得到基于混沌对立的学习策略。本文采用Sine映射,数学模型为
XTo=LB+UB+λ·X(k)
(21)
式中:XTo,λ——种群中当前黏菌个体对应的混沌反向解和混沌映射值。
参数a的变化对迭代过程中开发和探索的平衡有重要影响。由式(20)可知,a在早期迭代中迅速下降,在后期迭代中下降速度减慢,不利于全局探索。为了提高全局探索能力和局部开发的收敛能力[16],可将a定义为
a=2.5(k/kmax)2k/kmax
(22)
算术优化算法根据算术操作符的分布特性来实现全局寻优,与SMA结合后,可以有效改善SMA后期易陷入局部最优的缺点,增强算法后期寻优随机性。改进SMA(以下简称“ISMA”)在更新黏菌位置时,若r1 (23) 式中:pMO——数学优化器概率; ε——极小值; μ——控制参数; r2——随机数,且r2∈[0,1]。 选用Sphere、Ackley、Griewank、Rosenbrock 4种标准测试函数对PSO算法、GWO算法、SSA、SMA和ISMA的优化结果进行对比,标准测试函数相关参数如表1所示。 表1 4种标准测试函数相关参数 4种标准测试函数优化曲线如图2所示。由图2可知,相比其他4种算法,ISMA在收敛精度和速度上具有较大的优势。 图2 4种标准测试函数优化曲线 本文以某工业园区为研究对象,每24 h为一个运行周期,单位运行时间为1 h。系统中各设备关键参数如表2所示,分时购电电价如表3所示。售电价格为0.5元/kWh,天然气价格为2.55元/m3。系统典型日初始负荷、风电和光伏输出功率预测曲线如图3所示。 表2 系统中各设备关键参数 表3 分时购电电价 图3 系统典型日初始负荷、风电和光伏输出功率预测曲线 考虑IDR前后系统的电、热、冷负荷对比曲线如图4所示。由图4可以看出,原始负荷曲线显示出明显的峰、平、谷分布,当系统考虑IDR时,电、热、冷负荷峰谷差分别降低了22.1%,19.3%,17.9%,有效实现了“削峰填谷”,提升了IES的经济性。 图4 考虑IDR前后系统的电、热、冷负荷对比 为了验证ISMA的有效性,针对系统的目标函数,分别采用PSO算法、GWO算法、SSA、SMA和ISMA进行计算。不同算法的优化调度结果对比如表4所示。 表4 不同算法的优化调度结果对比 分析表4中不同算法得到的最优值发现,ISMA可以找到更好的最优解,总成本和碳排放量均低于其他算法。分别以运行成本最小和以碳排放成本最小为目标,用ISMA得到的IES典型日目标函数的电、热、冷负荷平衡分布,其分布情况如图5和图6所示。 图5 以运行成本最小为目标的负荷平衡分布 图6 以碳排放成本最小为目标的负荷平衡分布 分析图5和图6的ISMA优化调度结果,可以得出以下结论。电负荷优先由可再生能源WT和PV提供,当电能不足时,由GT发电或从电网购买电能。当考虑系统运行成本最小为目标时,在0:00—8:00分时电价为谷价期间,增加向电网的购电量,以减小系统运行成本;当考虑系统碳排放成本最小为目标时,由于GT的碳排放量比电网小,因此考虑增加GT发电功率。在12:00—17:00 WT和PV发电高峰期间,系统除满足电负荷需求外,多余的电能可以通过EC以及EB释放冷热能,做到多能互补,增加风光消纳,还可以售卖给电网。另外,ES可以在满足用户电负荷后,存储多余的电能,当电负荷不足时,放电以补足电能。 对于热负荷,优先使用WHB产生的热能,不足部分由GB以及EB补充。 冷负荷在电能充足时段,利用多余电能带动EC制冷,其余时段则由AC制冷。 本文研究了计及IDR的IES的优化调度问题,分别构建了以系统运行成本最小和系统碳排放成本最小的目标函数,对SMA进行改进得到ISMA,通过算例仿真结果得出以下结论。 (1) 考虑IDR时,电、热、冷负荷峰谷差分别降低了22.1%,19.3%,17.9%,提高了系统经济性。 (2) 选用标准测试函数对比分析ISMA与PSO算法、GWO算法、SSA、SMA的优化曲线,ISMA算法在优化速度和精度上具有明显优势。 (3) 对比分析ISMA与PSO算法、GWO算法、SSA、SMA分别用于IES调度时的系统运行成本和碳排放成本,并分析ISMA参与调度的电、热、冷负荷平衡分布情况,发现ISMA在保证系统稳定运行的同时,能够有效降低运行成本与碳排放成本。这可以为IES的实际运行调度提供参考。4 算例分析
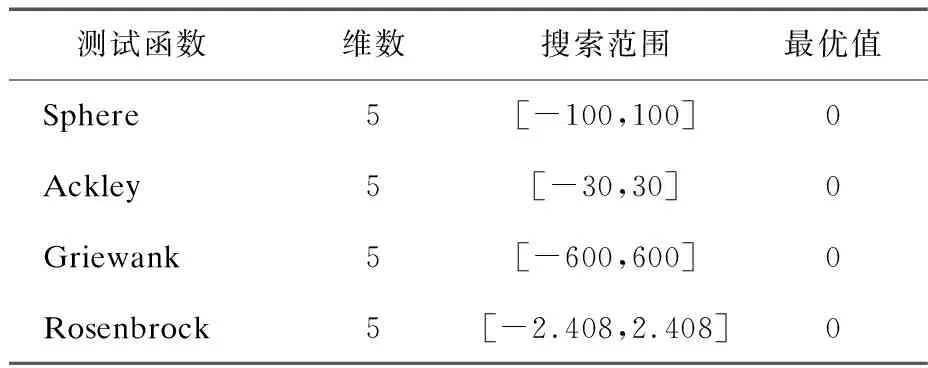
4.1 测试函数仿真

4.2 基础数据整理



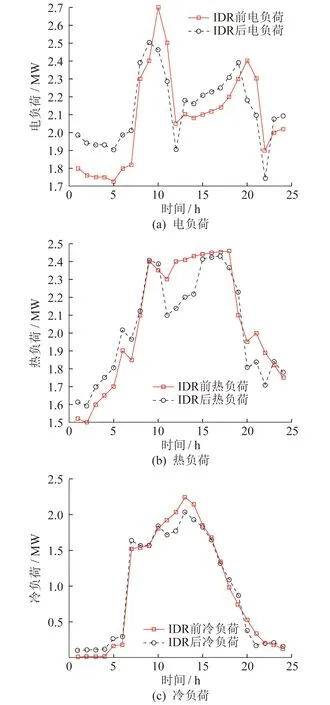
4.3 IDR结果分析
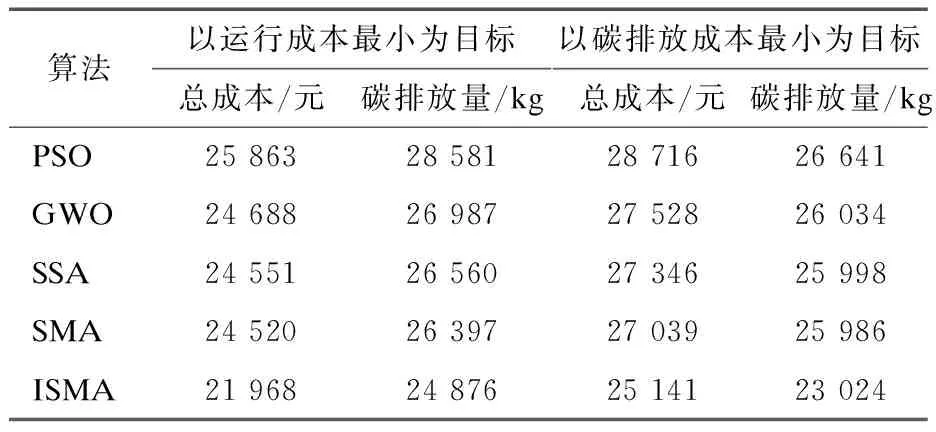
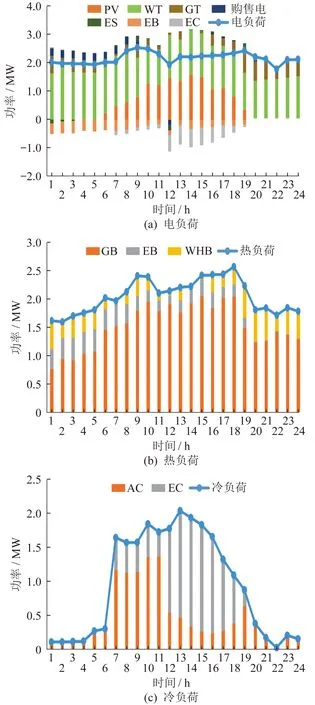
4.4 调度结果分析

5 结 论
