一种新角度支配关系的多目标进化算法
2024-03-06张浩楠过晓芳
张浩楠,过晓芳
(西安工业大学 基础学院,西安 710021)
在科学研究和工程领域中,经常会遇到同时需要优化多个目标的最优化问题,即多目标优化问题[1]。多目标优化问题中的特点是解之间相互冲突,最优解不是唯一的,而是一组互不支配的折中解,称为Pareto最优解[2]。随着目标个数的增加,最优解集合的数量不断增大,算法计算量越来越大,运用传统的多目标优化算法求解变得非常困难[3]。由于多目标进化算法基于种群的特性能够在一次运行中获得一组折中解,并且其不对所求问题需满足的数学性质等做出要求,因此多目标进化算法已广泛应用于各种多目标优化问题的求解[4-6]。目前,多目标进化算法求解多目标优化问题大致分为以下三类:基于支配的多目标进化算法[7-8],基于分解的多目标进化算法[9-11]以及基于指标的多目标进化算法[12-14]。
在求解高维的多目标优化问题的时候,随着优化目标个数的增加,传统的Pareto支配无法提供足够的选择压力[15]。基于支配的多目标进化算法能够更好地提高解的选择压力,因此研究者们从不同视角提出了多种改进的支配关系。现阶段,支配关系大致可分为以下几类:① 基于支配区域扩展的方法。文献[16-17]提出了α-支配,该支配准则的基本思想是在两个目标之间设置折衷率的上、下界,使得种群中性能较差的DRSs被支配,减少种群中非支配解比例,增加选择压力,提升算法的收敛性。但该支配准则中的参数值α不易设置,较难找到一个分布、收敛均良好的折中解集。文献[18]提出了控制支配区域支配方法(CDAS),该方法通过自定义参数S控制解支配区域的扩张或收缩程度,从而达到提升收敛性或增强多样性的目的。但CDAS的参数S在面对不同的问题时不容易确定,并且其难以同时提高解集的收敛性或多样性。文献[19]针对CDAS中参数不易设置进行改进,提出自控制支配区域支配方法(S-CDAS),该算法在比较二者支配关系时,不需使用外部参数S可自行控制每个解的支配面积,实现了解集收敛性和多样性之间更好的平衡。该类方法能够有效地增加解的选择压力,但没有兼顾多样性,会使非支配解集集中在Pareto前沿的某一部分,边界解可能会被支配。② 基于网格的方法。文献[20-21]提出了ε-支配。该支配准则通过将目标空间划分为多个超立方体网格,在扩大支配区域的同时,保证每个网格中只存在一个非支配解,既增大选择压力,也维持了分布的均匀性。但采用ε-支配的算法进行进化迭代的过程中,最优前沿上一些极端解容易被其他解支配,导致边界解丢失,多样性不够理想。文献[22]提出了Grid支配,该支配方法在ε-支配需自行设置参数的基础上进行改进,采用自适应网格结构,并且通过解的位置采用单独居中的网格进行计算,在增加算法选择压力的同时,维护种群的多样性。但该支配方法可能会消除相邻的良好收敛解,从而导致算法收敛性能降低。该类方法通过将目标空间划分为多个网格,以保证种群的多样性,同时扩大解的支配区域,从而提高了选择压力,但该类算法的网格规模不易选取,时间复杂度较大。③ 基于小生境的方法。文献[23]提出了增强支配关系的准则(SDR),该支配方法不需要用户预先定义,根据种群的分布自定义定制支配区域,并在此区域中搜索收敛性最佳的解,从而更好地平衡了解集的收敛性和多样性,但该算法性能差异同领域定制的规则紧密相关。该类方法能够保证解的多样性,但对复杂Pareto前沿的求解效果不太理想。④ 基于角度的方法。文献[24]提出了角度支配(AD支配),该支配方法通过构建由解和各轴节点组成的角度向量进行非支配排序,由于角度向量与坐标轴紧密相关,靠近PF和边界的解具有较高的非支配排序等级。因此AD支配在扩大解的支配区域的同时,又能有效地保持边界解,兼顾了解集的收敛性和分布的广泛性,但采用角度支配时解集均匀性仍可提升。该类方法增加解之间的选择压力,以保证解的收敛性,但解集的多样性不能很好地保证。
尽管以上改进的支配关系明显增强了算法求解的性能,但均无法更好地兼顾收敛性和多样性。采用ε-支配和AD支配的算法,都通过扩大解支配区域的方法提高算法的收敛性。基于网格的支配方法确保每个网格中只存在一个非支配解,维持解集分布的均匀性,但存在边界解丢失的问题,导致解集分布广泛性不够理想。AD支配使得靠近PF和边界的解具有较高的非支配排序等级,能有效地保持边界解,维持解集分布多样性,但均匀性仍有提高的余地。基于此,文中将ε-支配与AD支配进行有效结合,拟提出了一种网格-角度支配关系(Epsilon-Angle Dominance Relation,ε-AD)。该支配关系具有如下特点:①ε-AD支配在以上两种支配方法的基础上,进一步扩大解的支配区域,提升算法的收敛性;② 利用AD支配准则偏好边界解这一特性,ε-AD支配在进化过程中可有效保持边界解,提升解集分布的广泛性;③ε-AD支配基于网格的支配方式,保证每个网格中只能有一个非支配解,维持解分布的均匀性。文中将ε-AD支配嵌入到经典NSGAII算法框架中代替原有的Pareto支配,设计了一种新角度支配关系的多目标进化算法(Epsilon-Angle-NSGAII,ε-AD-NSGAII)。
1 新角度支配关系的多目标进化算法
文中给出多目标优化相关概念和定义,给出新的角度支配关系定义,将新支配关系嵌入到NSGAII算法中,提出一种新角度支配关系的多目标进化算法:ε-AD-NSGAII。
1.1 多目标优化相关概念和定义
定义1多目标优化问题。多目标问题一般描述为
minf(x)=(f1(x),f2(x),…,fm(x)),
(1)
式中:x=(x1,x2,…,xn)为n维决策空间中的解;fm(x)为第m个子目标函数。
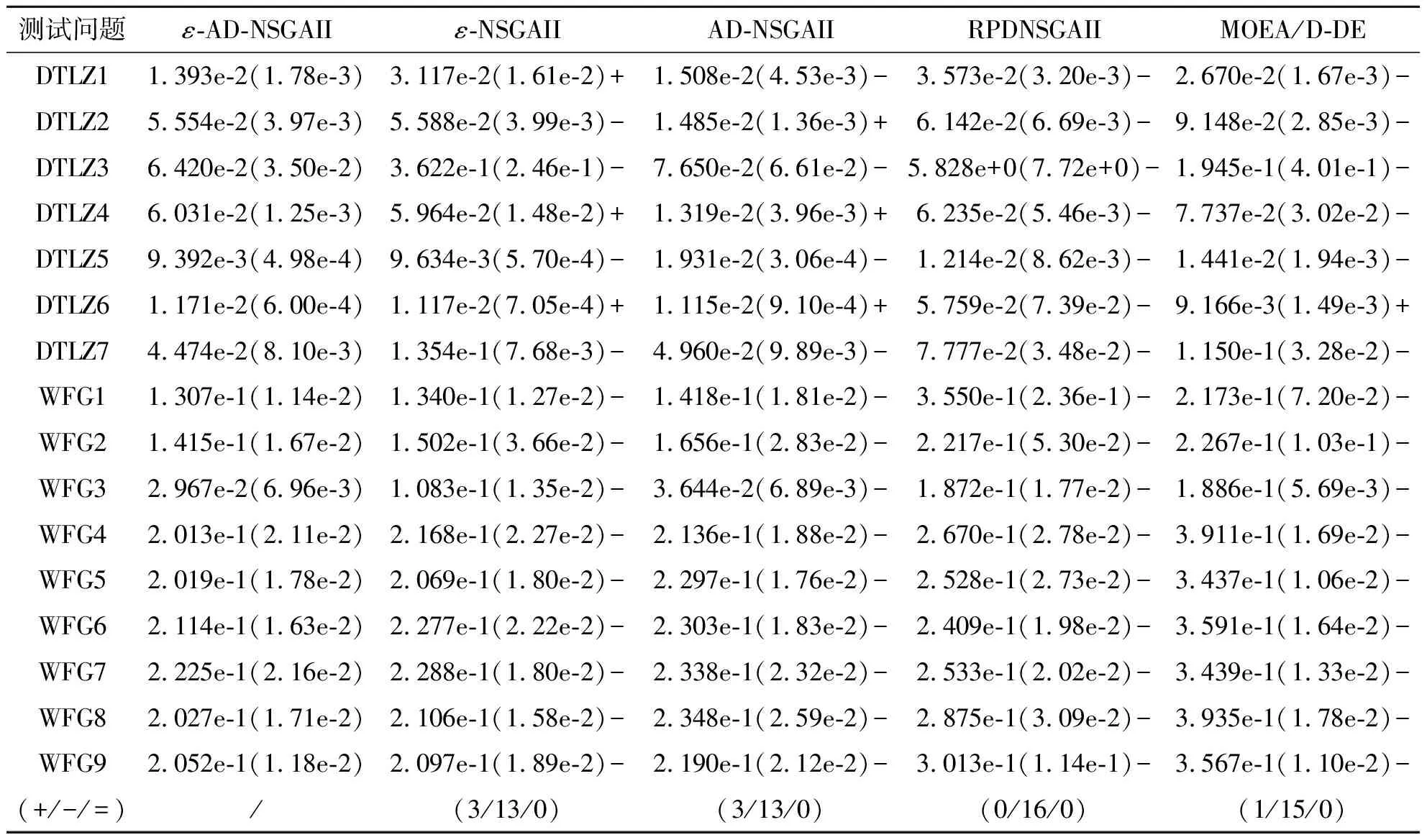
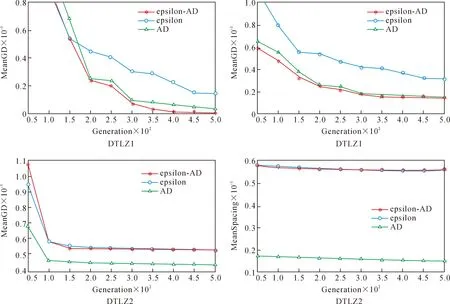
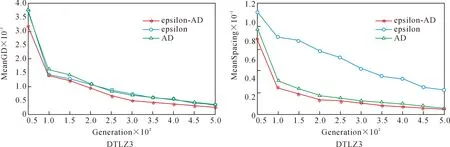
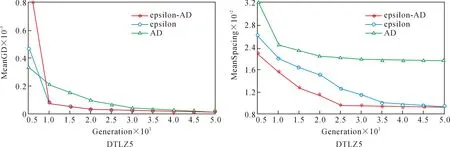
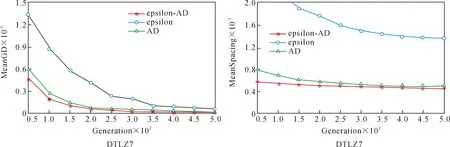
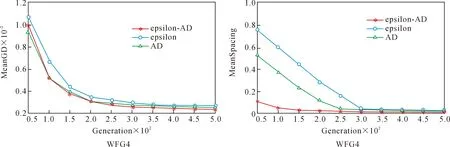
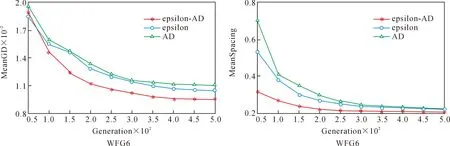
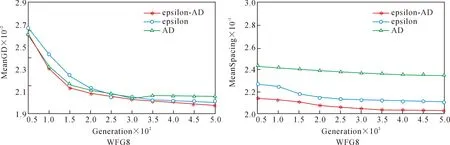
定义2Pareto支配。对于式(1)中的MOP问题,设x,y为决策空间中任意两个解,称x支配y(记为x (2) 定义3ε-支配。对于式(1)中的MOP问题,设x,y为决策空间中任意两个解,称xε-支配y(记为x<εy)当且仅当满足以下条件: 图1为ε-支配概念图,从图1中可以看出,若解x,y根据Pareto支配关系进行比较,二者之间没有支配关系。但若按ε-支配关系的定义,解x支配的区域为阴影区域,此时x<εy。 图1 ε-支配概念图 定义4AD支配。对于式(1)中的MOP问题,设x,y为决策空间中任意两个解,称xAD支配y(记为x (4) 图2为AD支配概念图,从图2中可以看出,若解x,y根据Pareto支配关系进行比较,二者之间没有支配关系。但若按照AD支配关系进行比较,支配区域扩张,此时x 图2 AD支配概念图 为直观解释所提出的ε-AD支配的概念,图3为此支配关系在两目标空间下的情景,阴影部分为当前种群中任意解x的ε-AD支配区域。如图3所示,假设比较任意两个解x和y间的优劣,若两个解之间距离小于阈值λ,选用ε-支配计算其适应度值,以提升接近Pareto前沿时解分布的均匀性;若两个解之间距离大于或等于阈值λ,选用AD支配计算其适应度值,降低了远离Pareto前沿时优秀解被支配掉的概率。解x经过ε-AD支配后的适应度向量为f(x)=(f1(x),f2(x)),见定义5,而fi(x)的计算见式(5)。 图3 ε-AD支配概念图 定义5设x,y为决策空间中任意两个解,x经过ε-AD支配后的适应度向量的第i个分量fi(x)定义为 (5) 定义6对于式(1)中的MOP问题,设x,y为决策空间中任意两个解,称xε-AD支配y(记为x<ε-angley)当且仅当满足以下条件: (6) 文中以NSGAII算法为例说明如何将ε-AD支配整合到基于Pareto支配的算法框架中。 算法1ε-AD支配方法 输入:种群P中任意两个解x、y,解之间的对比阈值λ 输出:x、y之间的ε-AD支配关系 Step 1:计算x、y间欧式距离d。 Step 3:当d≥λ时,若xAD支配y,则xε-AD支配y;若yAD支配x,则yε-AD支配x;否则,x、y互不ε-AD支配。 Step 4:当d<λ时,若xε-支配y,则xε-AD支配y;若yε-支配x,则yε-AD支配x;否则,x、y互不ε-AD支配。 Step 5:输出任意两个解x、y间的ε-AD支配关系比较。 算法2新角度支配关系的多目标进化算法 输入:种群规模N,最大迭代次数Tmaxgen 输出:最末代种群Pmaxgen Step 1:初始化迭代计数器t=0。 Step 2:随机生成种群大小为N的初始种群P。 Step 3:根据二元锦标赛选择法构建交配池Pmating。 Step 4:对Pmating进行交叉、变异操作,产生子代种群Q。 Step 5:合并父代种群P和子代种群Q:R=P∪Q。 Step 6:根据算法 1对中间种群R中任意两个解间的ε-AD支配关系进行比较。 Step 7:根据ε-AD支配关系将种群P划分为l层的非支配层(F1,F2,…,Fl)。 Step 8:当满足|P+Fj|≤N,则P=P∪Fj。 Step 9:当|P+Fj|≤N,计算Fj的拥挤距离。 Step 10:从Fj中删除k个拥挤距离最大的解:k=|P|+|Fj|-N。 Step 11:Fj中保留下的解和P构成新的种群P。 Step 12:重复步骤3到步骤11,直至达到最大迭代次数Tmaxgen,转至步骤13。 Step 13:输出最末代种群Pmaxgen。 对采用ε-AD支配的一次种群排序过程来说,N为种群大小,M为目标数,其步骤为:① 计算每个个体在每个目标下的角度值,其时间复杂度为O(N*M);② 计算每个个体在每个目标下的网格适应度值,其时间复杂度为O(1);③ 进行非支配排序,其时间复杂度为O(N2)。综上,采用ε-AD支配的一次种群排序过程的时间复杂度为O(M*N+N2)。 文中采用GD[25],IGD[26]和SPACING[27]评价指标,选取DTLZ[28]和WFG[29]测试问题集,将ε-AD-NSGAII与其他四种多目标进化算法的性能进行比较。关于对比算法的选取,将ε-支配和AD支配嵌入NSGAII框架,构造ε-NSGAII和AD-NSGAII,作为改进支配关系的对比算法。选择目前新提出的基于参考点支配的RPDNSGAII和基于差分的多目标进化算法MOEA/D-DE作为另外两个对比算法。将五类算法生成解集合的收敛性和分布性进行比较。 2.1.1 测试问题 文中实验选用3个优化目标下的DTLZ和WFG两个系列的测试问题,考察算法求解多目标优化问题的能力。上述两个测试问题集具有多种Pareto前沿特征,其中DTLZ测试问题集包含具有非凸、有偏、不连续、多模、混合等问题特性的测试函数,WFG测试问题集包含具有欺骗、偏转、多模等问题特性的测试函数,以及一组包含多种几何结构的形状函数。为了保证实验公正性,文中实验均在CPU 3.70 GHz、内存16 GB的PC上运行,所有算法均在PlatEMO平台上运行,编程工具为Matlab R2018a。 2.1.2 评价指标 为综合评估算法的收敛性和多样性,文中采用以下3个性能指标,即世代距离(GD)、反转世代距离(IGD)和空间评价方法(Spacing)。综合3个性能指标,能够很好地度量解集的收敛性和多样性。 采用GD度量作为收敛性评价指标,它表示算法所求得的非支配解集PFknown中的个体与Pareto最优解集PFtrue之间的距离,其表达式为 (7) 式中:n为PFknown中的向量数;p为2;di为所获得解集中向量与PFtrue中最近向量之间的欧氏距离。该指标越低,表示算法的收敛性越好。 采用IGD评价指标,度量了Pareto最优解集PFtrue中的个体到算法所求得的非支配解集PFknown的平均距离,其表达式为 (8) 采用Spacing评价指标,能够衡量算法所求得的非支配解集PFknown中个体的分布是否均匀,其表达式为 (9) 2.1.3 参数设置 文中5种算法的对比实验均采用以下设置:进化种群规模为100,每次运行最大评估次数为50 000,进行交叉操作时使用模拟二进制交叉算子(SBX算子),交叉率pc为1,进行变异操作时使用多项式变异算子(PM算子),变异率pm为1/n(n为决策变量数目),交叉、变异算子参数ηc及ηm均为20。另外,采用DTLZ和WFG测试问题时,网格大小ε取值为0.001~0.2,放大系数k取值为30~60,阈值λ取值为0.005~1。 为验证ε-AD支配在多目标优化中的有效性,用ε-AD支配、AD支配和ε-支配替换NSGAII算法中的pareto支配,构造ε-AD-NSGAII、AD-NSGAII以及ε-NSGAII算法,将ε-AD-NSGAII与ε-NSGAII、AD-NSGAII、RPDNSGAII以及MOEA/D-DE算法进行比较。为减少随机因素对算法性能评估的影响,将上述5种算法在所有测试问题上均独立运行30次。表1~表3给出算法性能指标的统计结果,加粗标记为对应指标上表现更好,(+/-/=)为一致性检验结果。 表1 5种算法在DTLZ和WFG问题集上获得的GD均值与标准差 2.2.1 不同测试问题中的GD比较分析 分析ε-AD-NSGAII与ε-NSGAII、AD-NSGAII、RPDNSGAII以及MOEA/D-DE在解决多目标优化问题时收敛性上的差别。表1给出了上述5种算法在DTLZ和WFG测试问题集中16个测试问题上所获得的GD均值与标准差。由表1可知,在16个测试问题中,ε-AD-NSGAII获得了8个最佳GD均值,RPDNSGAII获得了4个最佳GD均值,AD-NSGAII获得了3个最佳GD均值,MOEA/D-DE获得了1个最佳GD均值,ε-NSGAII没有获得最佳GD均值。同时由一致性检验结果可知,与ε-NSGAII、AD-NSGAII、RPDNSGAII和MOEA/D-DE相比,ε-AD-NSGAII分别在14、13、12和14个测试问题上有更好的表现。由于使用ε-AD支配的进化算法在大多数问题上都能获得更好的收敛性,因此使用ε-AD支配的进化算法在解决多目标优化问题上更能快速、准确得找到最优解集,具备较好的收敛性。 2.2.2 不同测试问题中的IGD比较分析 分析ε-AD-NSGAII与ε-NSGAII、AD-NSGAII、RPDNSGAII以及MOEA/D-DE在在解决多目标优化问题时收敛性和多样性上的差别。表2给出了上述5种算法在DTLZ和WFG测试问题集中16个测试问题上所获得的IGD均值与标准差。由一致性检验结果可知,在16个测试问题中,与ε-NSGAII、AD-NSGAII、RPDNSGAII和MOEA/D-DE相比,ε-AD-NSGAII分别在15、15、8和15个测试问题上有更好的表现。由此可见,新提出的算法较之ε-NSGAII、AD-NSGAII和MOEA/D-DE,具有明显较优的综合能力上的优势。关于ε-AD-NSGAII与RPDNSGAII的对比分析,ε-AD-NSGAII采用一种将ε-支配和AD支配进行有效结合的支配关系对解集进行排序,RPDNSGAII采用基于参考点的支配关系,能够使用一组分布良好的参考点对解集进行排序,以上两个算法都能在测试问题上取得相似的效果。综上,使用ε-AD支配的进化算法,其具有较优的收敛性和多样性之能力。 表2 5种算法在DTLZ和WFG问题集上获得的IGD均值与标准差 2.2.3 不同测试问题中的Spacing比较分析 分析ε-AD-NSGAII与ε-NSGAII、AD-NSGAII、RPDNSGAII以及MOEA/D-DE在解决多目标优化问题时分布的多样性上的差别。表3给出了上述5种算法在DTLZ和WFG测试问题集中16个测试问题上所获得的Spacing均值与标准差。由表3可知,在16个测试问题中,ε-AD-NSGAII获得了13个最佳Spacing均值,AD-NSGAII获得了2个最佳Spacing均值,MOEA/D-DE获得了1个最佳Spacing均值,RPDNSGAII和ε-AD-NSGAII没有获得最佳Spacing均值。同时由一致性检验结果可知,与ε-NSGAII、AD-NSGAII、RPDNSGAII和MOEA/D-DE相比,ε-AD-NSGAII分别在13、13、16和15个测试问题上有更好的表现。综上所述,使用ε-AD支配的进化算法求得的解集分布更均匀,ε-AD支配具有更优的多样性保持能力。 表3 5种算法在DTLZ和WFG问题集上获得的Spacing均值与标准差 2.2.4 不同测试问题中的收敛速度比较 为更加直观地比较ε-AD-NSGAII、ε-NSGAII和AD-NSGAII的寻优性能,选取3个优化目标下的DTLZ和WFG两个问题集作为测试问题,各算法在上述测试问题集上均独立执行30次取均值,每次运行最大评估次数为50 000,以获得稳定的GD和Spacing均值。图4~图11为3种算法在上述测试问题上的GD和Spacing指标的进化轨迹图。其中,横坐标为进化代数,纵坐标为指标值。 图4 3种算法在3维DTLZ1、DTLZ2测试函数上的GD、Spacing进化轨迹图 图5 3种算法在3维DTLZ3、DTLZ4测试函数上的GD、Spacing进化轨迹图 图6 3种算法在3维DTLZ5、DTLZ6测试函数上的GD、Spacing进化轨迹图 图7 3种算法在3维DTLZ7、WFG1测试函数上的GD、Spacing进化轨迹图 图8 3种算法在3维WFG2、WFG3测试函数上的GD、Spacing进化轨迹图 图9 3种算法在3维WFG4、WFG5测试函数上的GD、Spacing进化轨迹图 图10 3种算法在3维WFG6、WFG7测试函数上的GD、Spacing进化轨迹图 图11 3种算法在3维WFG8、WFG9测试函数上的GD、Spacing进化轨迹图 由图4~图11可以看出,三种算法随评估次数的增加,它们所获得的GD均值和Spacing均值都随进化代数的增长总体上呈下降趋势,并且都能较快地下降至一个相对较小的值,而在后续进化过程中,指标值呈现出缓慢变小的趋势。但对大多数问题而言,ε-AD-NSGAII算法获得的GD均值和Spacing均值是在三者中下降最快的。因此,图4~图11中各算法获得的轨迹直观地表明了ε-AD-NSGAII算法比其他两种算法能够较快地获得高质量解集。 1) 为有效平衡多目标进化算法的收敛性和多样性,论文提出一种网格-角度支配关系,并将此策略嵌入到经典NSGAII算法框架中代替原有的Pareto支配,设计了一种基于网格-角度支配的ε-AD-NSGAII算法。该算法通过将ε-支配与AD支配进行有效结合,在扩大解支配区域以提升算法收敛性的基础上,能够维持解集分布的均匀性以及保持边界解,有效提升算法所获得解集的多样性。 2) 文中基于DTLZ和WFG测试问题集,采用GD、IGD、Spacing三种评价指标,分别评估了ε-AD-NSGAII、ε-NSGAII、AD-NSGAII、RPDNSGAII以及MOEA/D-DE的有效性。实验结果表明,在16个测试问题中,ε-AD-NSGAII算法分别取得了8个最佳的GD指标值、7个最佳的IGD指标值以及13个最佳的Spacing指标值,由此表明ε-AD-NSGAII算法较之其余4种算法具有较好的收敛性和多样性。同时,通过对比ε-AD-NSGAII、ε-NSGAII、AD-NSGAII在上述测试集获得的GD和Spacing指标的进化轨迹图,可知ε-AD-NSGAII算法相比其余2种算法能够较快地获得高质量解集。 3) 在未来的工作中,进一步将网格-角度支配关系嵌入不同算法框架中,研究其对收敛性和多样性的影响,求解高维多目标优化问题,以及使用网格-角度支配关系的算法求解现实中的多目标优化问题,并不断改进算法的性能。


1.2 网格-角度支配
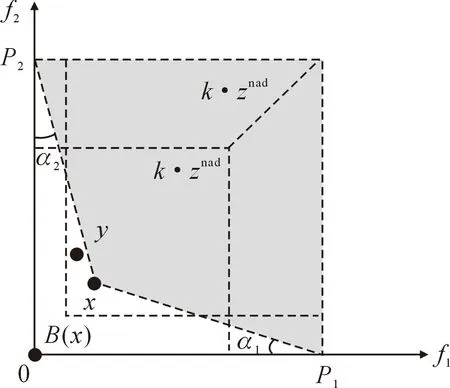


1.3 新角度支配关系的多目标进化算法

1.4 时间复杂度分析
2 实验结果与分析
2.1 测试问题、评价指标及其相关参数设置

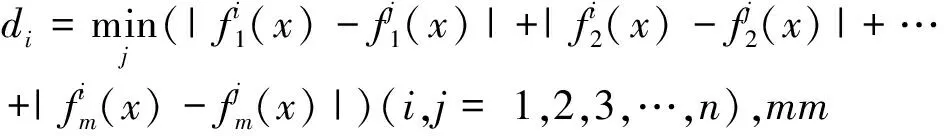
2.2 结果与分析



3 结 论
