基于监督下降法的大地电磁二维反演及应用研究
2024-03-06付兴谭捍东董岩汪茂
付兴,谭捍东,董岩,汪茂
(中国地质大学(北京) 地球物理与信息技术学院,北京 100083)
0 引言
大地电磁测深法(MT)是一种通过观测天然交变电磁场来对地电构造进行研究的物探方法,大地电磁法的频域很宽,其探测深度距地表有几百米到数百公里不等,具有分辨率高,穿透能力强,勘探深度大以及效率高等实际优点,被广泛应用于金属矿产普查、勘探地热和油气田等领域[1]。
大地电磁二维反演常采用高斯牛顿法[2]、OCCAM法[3]、非线性共轭梯度法[4]等,这些方法在最小化目标函数时各有优劣,但都无法在迭代过程中避免雅可比矩阵或海森矩阵的计算,且存在陷入局部极小值的风险,导致反演效果变差。
近些年随着计算机行业的发展,机器学习成功在多种领域取得不错的效果[5]。机器学习能够挖掘变量与标签之间的关联,并学习其关联进行预测,大大减少反演时间,提升计算效率[6]。
监督下降法(SDM)在人脸识别技术中被广泛使用[7-8],后被带入到多领域进行研究[9-11]。采取监督下降法解决地球物理勘探领域的问题也取得了不错的成效[12],模型与正演响应合并构成的训练集在进行一维瞬变电磁(TEM)反演中发挥了重要的作用[13]。监督下降法分为离线训练和在线预测两个阶段,在离线训练阶段,通过学习大量模型及其响应得出平均下降步长。在预测阶段,采用学习的步长进行迭代预测。平均步长具有较好的指导作用,避免了迭代陷入局部极小的风险,提升了反演的效果。此外,监督下降法并不需要计算雅可比矩阵和海森矩阵,避免了内存浪费的同时,提升了反演的效率。
本文采用监督下降法理论改进大地电磁二维数据反演算法,编写相关代码并设计理论模型验证算法的正确性,对其抗噪能力及实用性进行检验。相较于传统的非线性共轭梯度反演,基于监督下降法的反演具有收敛速度快、反演效果好、抗噪能力强等特点。
1 大地电磁二维正反演简介
1.1 大地电磁二维有限单元法正演
忽略位移电流和磁导率的影响,时间因子为e-iωt,大地电磁场满足麦克斯韦方程组:
(1)
式中:σ为介质的电导率;μ0为介质的磁导率;E为电场强度;H为磁感应强度。由式(1)可推导出赫姆霍兹方程组:
(2)
(3)
式中:AB为上边界,CD为下边界。
(4)
对图1所有单元进行离散,式(3)变为:
(5)

图1 部分单元网格Fig.1 Sketch of partial grid
式中:K为总体系数矩阵,求取式(5)的极值,可得
Ku=0,
(6)
可得出各节点的u,相应的视电阻率及阻抗相位为:

(7)
1.2 大地电磁二维非线性共轭梯度反演
常规的大地电磁二维反演方法有高斯牛顿法、OCCAM法、非线性共轭梯度法。本文将采用非线性共轭梯度反演与基于监督下降法的反演进行对比,下面概要介绍非线性共轭梯度反演方法。
定义大地电磁二维反演目标函数如下[15]:
Φ(m)=(dobs-F(m))TV-1(dobs-F(m))+
λ(m0-m)TLTL(m0-m),
(8)
式中:m为模型参数;F(m)为求取阻抗张量的正演函数;dobs为模型正演响应或实测数据;V为协方差矩阵;λ为正则化参数;L为二次差分拉普拉斯算子;m0为先验信息,目标函数具有数据拟合差最小和模型最光滑的双重约束。
目标函数的梯度为:
g=-2ATV-1e+2λLTL(m0-m),
(9)
其中:A表示雅可比矩阵,数据误差向量:e=dobs-F(m)。
非线性共轭梯度反演的具体步骤如下[16-17]:
1)i=0时,设定初始模型mi,计算梯度ri=gi;

3)求解ri=0,得出最优搜索步长αi;
4)mi+1=mi+αiui,ri+1=gi+1;
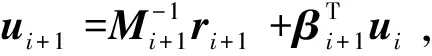
6)取i=i+1,回到步骤3),直至收敛,反演结束。
2 基于监督下降法的大地电磁二维反演
监督下降法运用机器学习理论,采取半监督学习方式,分为训练和预测两个阶段。训练阶段通过对训练集的学习,得到一组平均下降方向。预测阶段运用平均下降方向迭代计算数据残差,进而进行迭代。监督下降法的流程如图2。
2.1 训练阶段
在进行大地电磁反演计算时,定义目标函数如下:
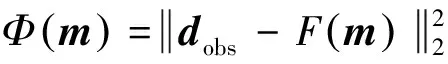
(10)
对式(10)的正演函数F(m)进行一阶Taylor展开,求取对m的极小值,可得:
Δm=(JTJ)-1JTΔd,
(11)
其中:J为雅可比矩阵;Δm=m-m1;Δd=dobs-F(m);α=(JTJ)-1JT,α为迭代步长。由于正演数据存在非线性,常规反演通常采取不断迭代的方式来求取Φ(m)关于m的极小值,计算雅可比矩阵及海森矩阵是在进行常规反演时较为消耗计算时间和占用内存空间的一步。况且,上述目标函数在此时容易陷入局部极小,所以,需要大量的模型迭代来获得迭代最优方向。
此时,相较于每次迭代均需计算雅可比矩阵或海森矩阵且每步均需搜索下降步长的常规大地电磁反演,引入机器学习的思想,通过学习的平均下降方向,使目标函数快速趋于极小值的方法可以节约大量计算时间以及大量内存空间,同时避免目标函数陷入局部极小值。
合成一组训练集(标签集MP和数据集DP),为了计算下降方向,求下式极小值:

(12)
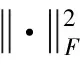
(13)
(14)

αi=(ΔDiTΔDi+λI)-1ΔDiTΔMi,
(15)
式中:i为迭代次数;λ为阻尼系数(可与相加的内容呈现比例关系),Mi+1表达式如下:
Mi+1=Mi+ΔDiαi,
(16)
在此阶段,数据拟合差RMSD与模型拟合差RMSM为:
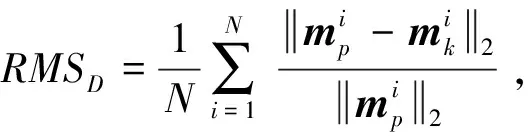
(17)
当模型拟合差趋于稳定、足够小或者达到了预设的最大迭代次数时,训练阶段结束。
2.2 预测阶段
将上阶段的平均步长用于该阶段的计算,具体过程如下:
mi+1=mi+[dobs-F(mi)]αi,
(18)
从i=1开始计算,m1与训练过程的初始模型相同。当F(mi)与dobs间的数据残差为0时,停止迭代,输出反演结果。
为解决反演的多解性问题,考虑在预测阶段加入吉洪诺夫正则化来解决这一问题。
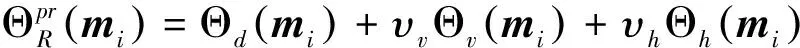
(19)
式(19)为进行正则化的目标函数,其中υv、υh为垂直方向以及水平方向的正则化系数。
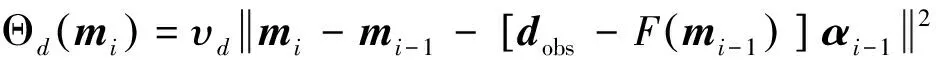
(20)
式中:
(21)
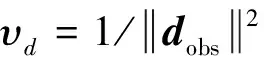
求取式(19)的极小值进行偏导处理,可得下式,化简后,可得
Gimi=di,
(22)
(23)
求解式(22),解出的mi,利用mi进行下次迭代,直至数据拟合差停止变小或小于一定数值,数据拟合差公式如下:
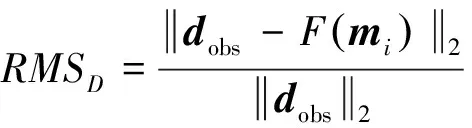
(24)
最大训练次数的步长预测完后,得出的数据拟合差未达到标准或者预测结果未达到期望,采取重启步长算法,即从第一个步长开始,进行新一轮的预测,直至数据拟合差足够小或不再减少。
3 理论模型合成数据二维反演算例
大地电磁的二维正演采用有限单元法,将地下介质剖分成33×26的网格单元,横向网格中心区域均匀剖分,两侧不断变大。纵向为26个不断增大的非均匀网格,设计40个频点。
将部分不同电阻率的规则形状的异常体在背景电阻率为100 Ω·m的均匀半空间内移动,形成了4 355个不同模型,如图3所示。

图3 部分训练集Fig.3 Some training samples
将上述模型分别进行正演计算,使用正演结果中TM模式的数据信息,将上述模型与正演响应构成一个训练集,进行离线训练,本阶段采用matlab及C++混合编程的方法,模型试算工作采用的CPU型号为i5-12500H,开启10线程并行,训练共耗时2 h。
训练过程共迭代8次,初始迭代误差为0.423,迭代8次后误差缩小为0.087。迭代过程如图4所示。从训练集中随机取出80组模型进行验证工作,其中数据误差低于15%的有80组(如图5所示),可见离线训练所求平均下降方向满足反演要求。
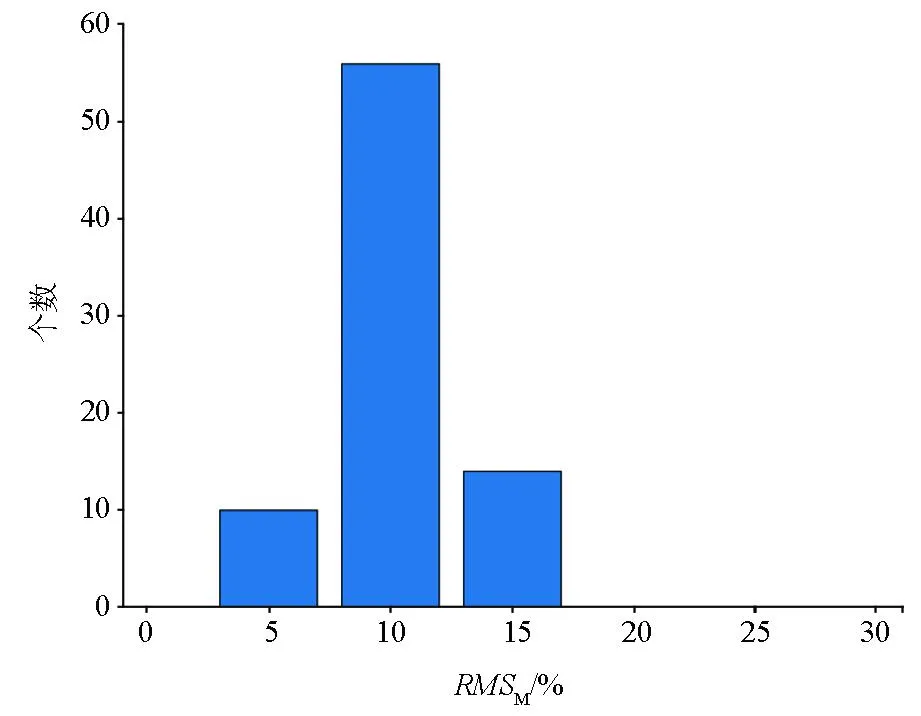
图5 误差分布Fig.5 The histogram of the normalized model misfit
3.1 理论模型1
模型1(图6)包含4个异常体,背景电阻率为100 Ω·m,异常体1是大小为800 m×800 m、埋深为400 m、电阻率值为1 000 Ω·m的高阻异常体,异常体2是大小为800 m×700 m、埋深为300 m、电阻率值为10 Ω·m的低阻异常体,异常体3是大小为600 m×700 m、埋深为300 m、电阻率值为1 000 Ω·m的高阻异常体,异常体4是大小为1 000 m×1 000 m、埋深为400 m、电阻率值为10 Ω·m的低阻异常体。

图6 理论模型1示意(从左到右分别为异常体1、2、3、4)Fig.6 Schematic diagram of model 1 (abnormal bodies 1, 2, 3 and 4 are arranged from left to right)
图7a为模型1正演响应的反演结果,图7b为10%高斯误差合成数据的反演结果,图8为两者的数据拟合曲线。可见,本算法具有一定的抗噪能力。

a—高斯误差为0%的预测结果 ;b—高斯误差为10%的预测结果
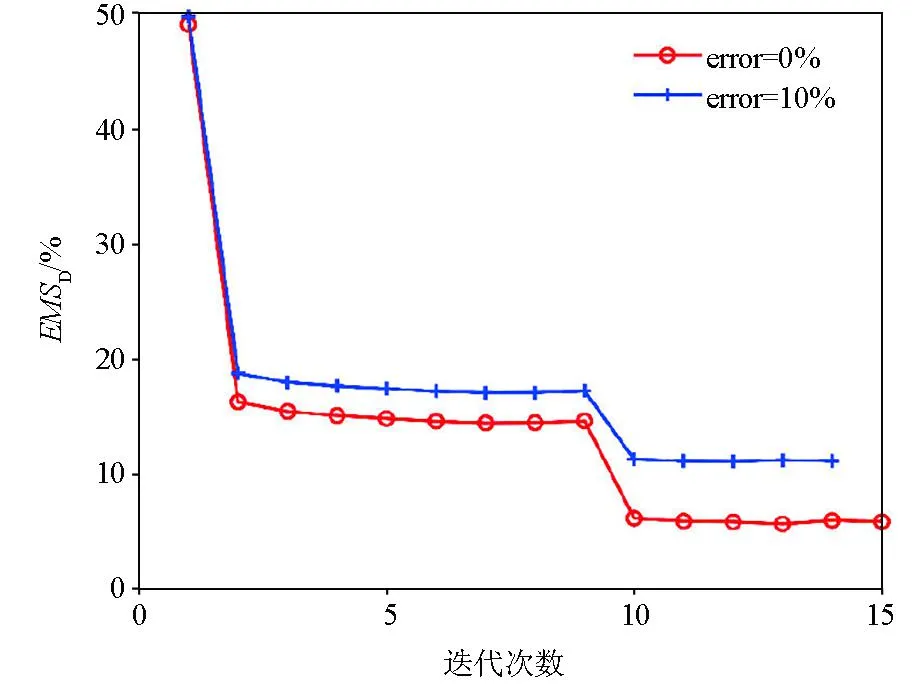
图8 迭代过程的数据拟合差Fig.8 The normalized data misfit in iteration
图9a为非线性共轭梯度法的二维反演结果,用时5.695 s。高阻异常体1、3均未能恢复理论模型电阻率,能还原异常体大致位置;低阻异常体2、4未能恢复理论模型电阻率,大致还原异常体位置。
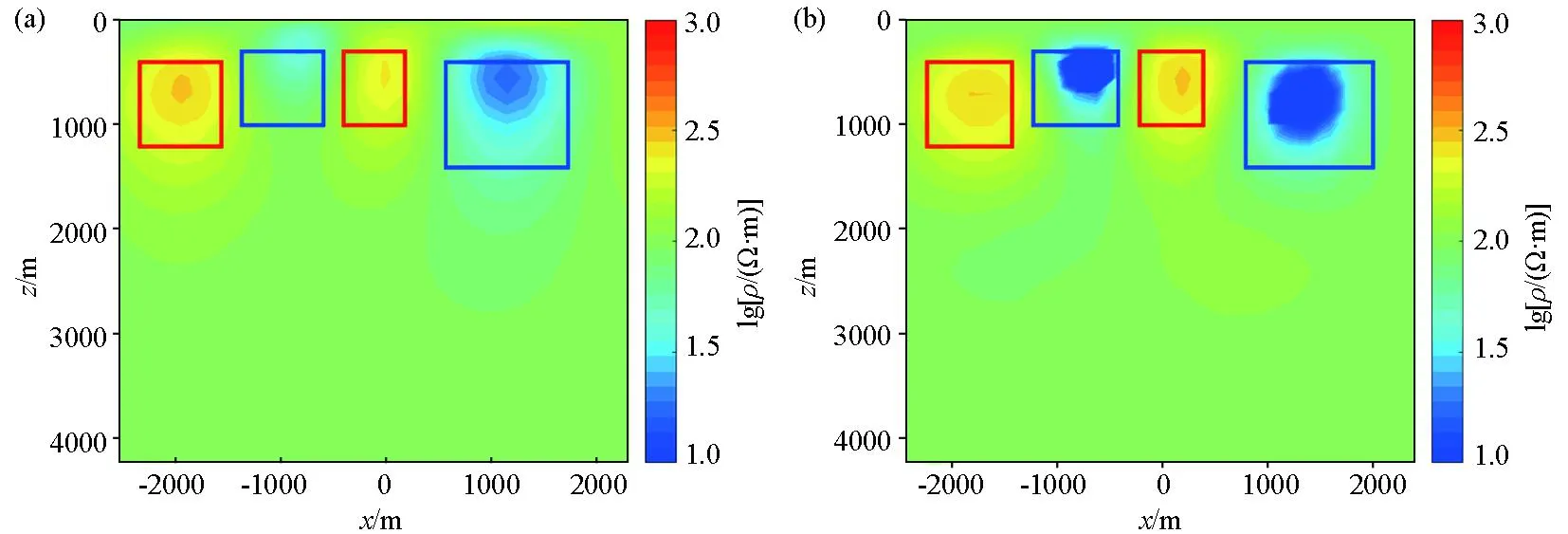
a—非线性共轭梯度反演结果;b—监督下降法反演结果
图9b为监督下降算法反演的结果,用时3.145 s。高阻异常体1、3理论模型电阻率的恢复效果优于图9a,且能够还原异常体位置;低阻异常体2、4的反演结果基本可以恢复理论模型电阻率,也能够还原异常体位置。
3.2 理论模型2
模型2(图10)包含4个异常体,背景电阻率为100 Ω·m,异常体1是大小为1 400 m×1 000 m、埋深为1 200 m、电阻率值为1 000 Ω·m的高阻异常体,异常体2是埋深300 m、电阻率值为10 Ω·m的阶梯状低阻异常体,异常体3是大小为1 200 m×260 m、埋深为40 m、电阻率值为10 Ω·m的低阻异常体,异常体4是大小为600 m×1 300 m、埋深为850 m、电阻率值为1 000 Ω·m的高阻异常体。
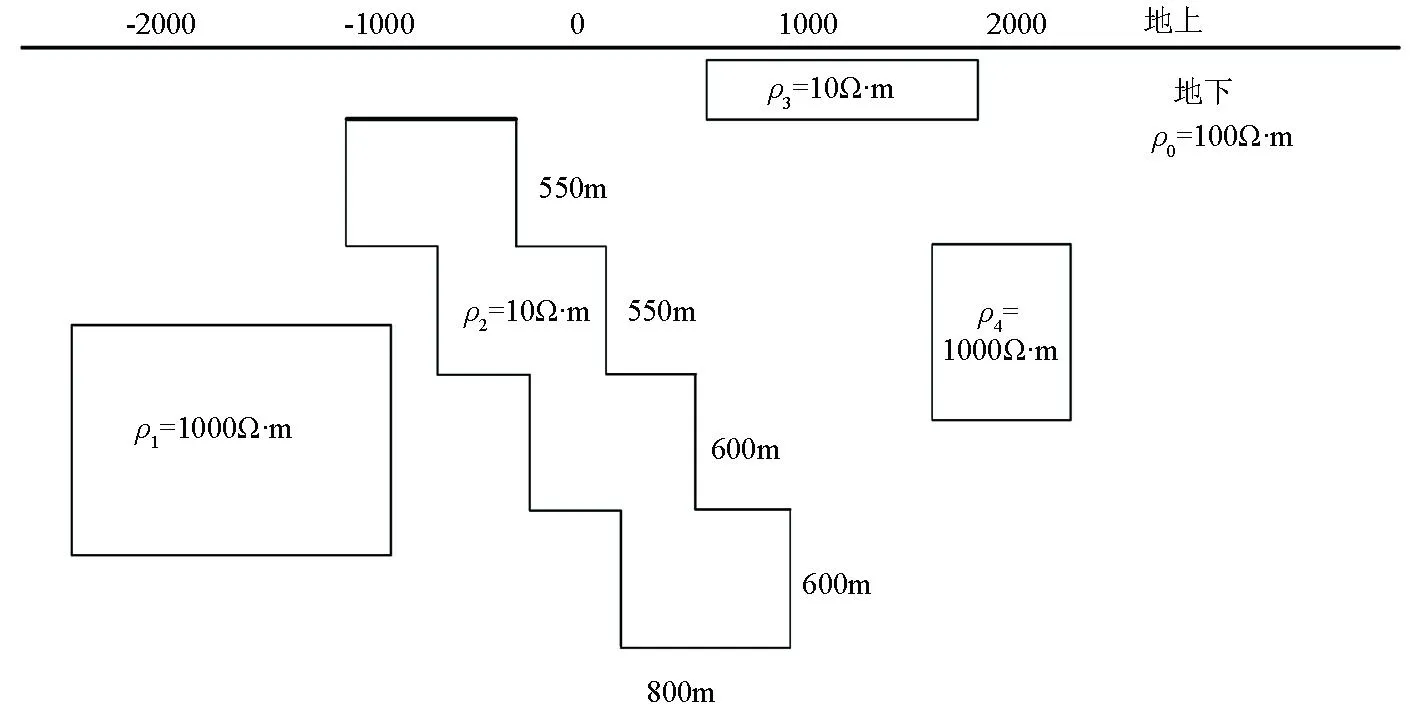
图10 理论模型2示意(从左到右分别为异常体1、2、3、4)Fig.10 Schematic diagram of model 2 (abnormal bodies 1, 2, 3 and 4 are arranged from left to right)
图11a为非线性共轭梯度法的二维反演的结果,用时5.6 s。高阻异常体1未能恢复理论模型的电阻率,也未能还原异常体位置;非线性共轭梯度反演方法仅恢复了低阻异常体2地下1 000 m以上的信息,但基本无法得出1 000 m以下的有效信息,可能受低阻异常体3的影响较大;低阻异常体3大致恢复理论模型的电阻率,并还原异常体位置;高阻异

a—非线性共轭梯度反演结果;b—监督下降法反演结果
常体4未恢复理论模型的电阻率,也未还原异常体大致位置。
图11b为监督下降算法反演的结果,初始迭代误差为0.546,迭代10次后迭代误差为0.063 1,用时2.8 s。高阻异常体1理论模型电阻率的恢复效果优于11a,且能还原异常体位置;监督下降算法可以反演出低阻阶梯状异常体2的地下2 000 m以上的异常体信息,并恢复异常体理论模型电阻率,2 000~3 000 m的部分没有很好的体现,可能是低阻异常体3屏蔽的影响;低阻异常体3能恢复理论模型的电阻率,也能还原异常体位置;高阻异常体4理论模型电阻率恢复效果优于11a,可能是低阻异常体3的影响,也未还原异常体位置。
3.3 理论模型3
模型3(图12)为复杂地层模型,背景电阻率为100 Ω·m,存在地层平均层厚500 m,顶部埋深100 m,电阻率值10 Ω·m的中部突起地层异常体。
图13a为非线性共轭梯度法的二维反演的结果,用时6.2 s。图13b为监督下降算法反演的结果,初始迭代误差为0.842,迭代10次后迭代误差为0.085,用时3.4 s。监督下降算法的形态更接近真实模型,对异常体的电阻率恢复效果更好。
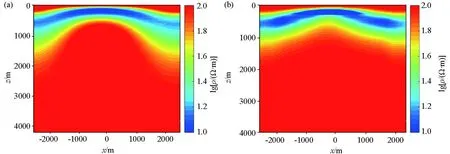
a—非线性共轭梯度反演结果;b—监督下降法反演结果
总体上,监督下降法的反演效果优于非线性共轭梯度法的反演效果。训练集中并没有训练较复杂的模型,但我们仍可以反演理论模型的高阻异常体、复杂异常体以及复杂地层异常模型,说明监督下降法具有处理较复杂模型的能力。
4 实测数据应用
为验证算法的实用性,将本文开发的反演算法应用于西藏高原南部雅鲁藏布江缝合带地区实测数据的反演。测线南起错那县,终止于墨竹工卡县,全长约240 km,测点29个,观测频率范围为0.000 1~250 Hz。测线横跨雅鲁藏布江缝合带,缝合带附近存在大规模的冈底斯花岗岩[18]。
图14为原始数据拟断面图,本文主要对TM模式的数据进行反演,对比监督下降算法及非线性共轭梯度算法反演结果,以此验证监督下降法的实用性。
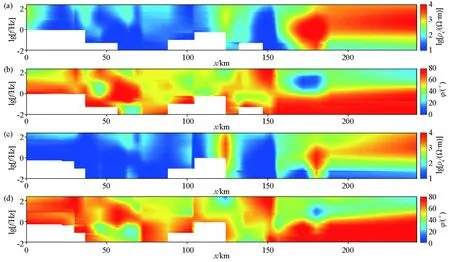
a—TM模式视电阻率拟断面;b—TM模式相位拟断面;c—TE模式视电阻率拟断面;d—TE模式相位拟断面
图15a为非线性共轭梯度法的反演结果,图15b为监督下降法的反演结果,两者反演结果基本一致。图16为反演结果与实测数据对比,可见大构造拟合程度较高。在时间方面,非线性共轭梯度大致需要30 s,监督下降法的训练时间为2 h左右,预测时间大约25 s。
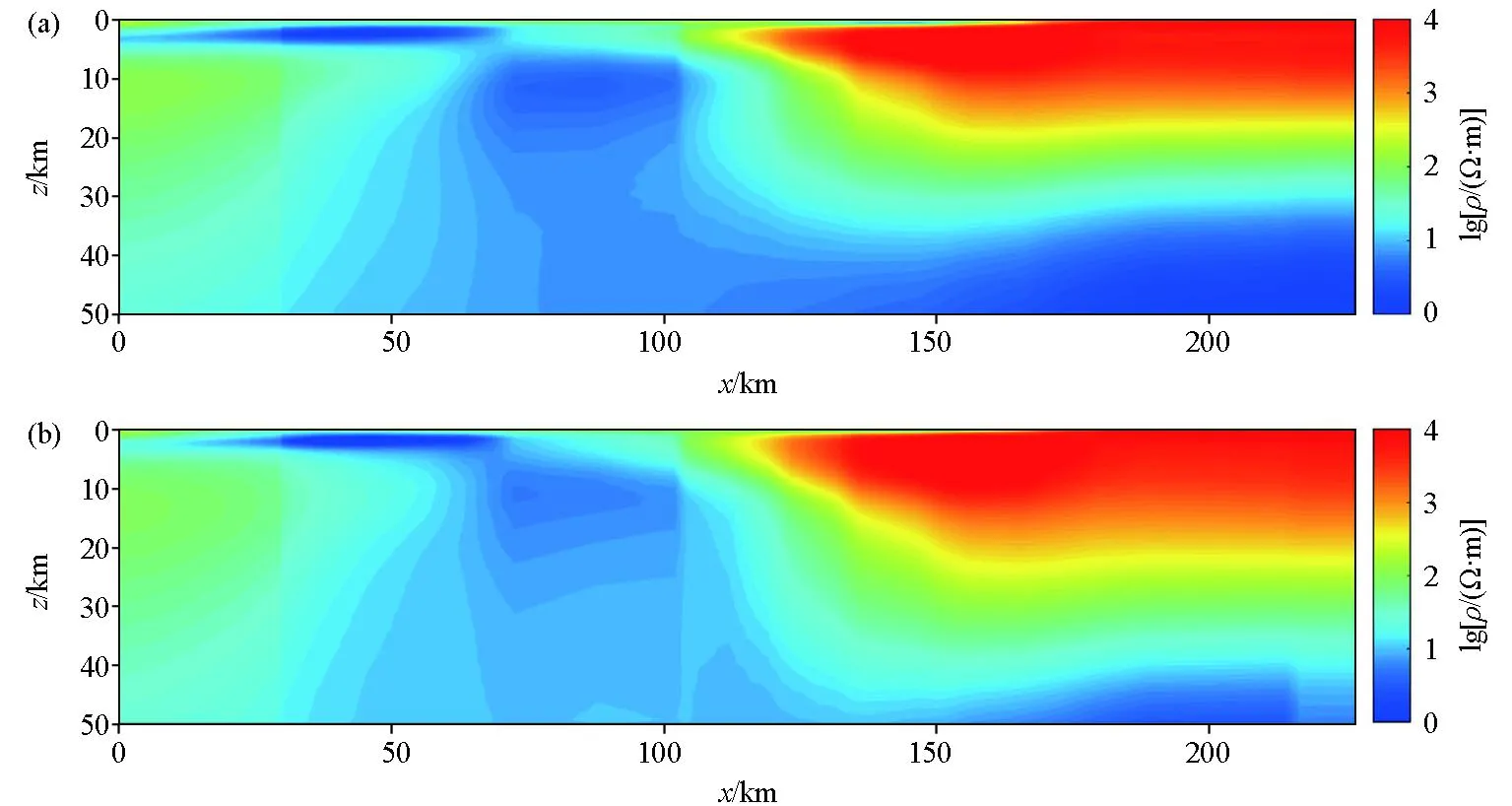
a—非线性共轭梯度法反演结果;b—监督下降法的反演结果
5 结论
本文实现了基于监督下降法的大地电磁二维反演,学习了一组训练集,对三组理论模型和实测数据进行了反演,检验了反演算法的可行性和实用性。反演结果表明基于监督下降法的大地电磁二维反演收敛速度、反演效果优于非线性共轭梯度反演,具有较好的抗噪能力及实用性。
1)训练得到的平均步长对异常体的预测起了指导性作用,避免了雅可比矩阵及海森矩阵的计算,大大降低了陷入局部极小值的风险,减少反演多解性。
2)就预测阶段来说,需要的时间小于常规反演所需的时间,对于批量数据的处理具有一定优势。
3)监督下降法具有较高泛化能力,可以用于更多地球物理勘探方法。
监督下降法总体耗时(训练+预测)较常规反演略长,同时平均步长的储存对硬盘的需求较大,并行降低耗时与减少储存是其未来的研究方向。
