集输管道临界携液流速计算模型研究

秦 虹，赵紫汐，姚佳杉，许开志，李 盼

1.中国石油华北油田公司第一采油厂，河北任丘 062552

2.中国石油华北油田公司第二采油厂，河北霸州 065700

3.中国石油华北油田公司第五采油厂，河北辛集 052360

目前，我国天然气、煤层气或伴生气的集输普遍采用气液混输（湿气输送）的方式。虽然在部分井场的井口装备了气液分离装置，但受管内温度、压力的影响，在一些低洼处仍不可避免地形成凝析液或水[1]。特别是近年来，我国油气资源逐渐从内陆向海洋、山区和沙漠发展，地形起伏带来的管内积液问题频繁发生，导致管道压降增大、低洼处腐蚀严重和下游设备频繁起跳等问题[2]。因此，研究气液混输过程中流体流动特性，分析起伏管道积液的形成原因和规律，对指导集输管道的设计及安全运行具有重要意义。

迄今，诸多学者已在地面集输管道的积液、压降或临界携液流速等方面进行了研究，刘晓倩等[3]研究了气体流速、管道倾角对管内持液率的影响，获得了不发生积液的临界倾角，但测试的倾角范围仅为-4°～4°，现场应用范围较小；陈建磊等[4]利用Wallis 提出的液泛公式作为临界携液流速的修正公式，但模型忽略了液相表观流速，且未经过现场验证。基于上述问题，基于多相流OLGA 软件和双流体模型确定了临界携液流速的预测方法，并模拟不同影响因素下的临界携液流速，进而通过均匀实验设计获取因素间的交互作用强度，最后通过随机森林模型完成非线性数据回归，并针对现场气井参数与文献中的模型方法进行对比。

1 临界携液流速预测方法研究

关于临界携液流速的预测方法有零液壁剪切应力模型、最小界面剪切应力模型、最小压降梯度模型和最小持液率模型等[5-6]。其中，王旭等[7]在实验中证明了以液滴或液膜反转作为产生积液的时机较实际时间偏早，Adewumi 等[8]证明了某些湿气管道在经过分离器分离后仍存在低液相负荷流动，说明前两个模型的适应性有待进一步验证。Landman等[9]证明在近水平的气液两相流动过程中，如仅改变气相流量，则通过动量方程计算出的持液率可能存在中间解不稳定的现象，特别当管道倾角较大或液相负荷较大时，持液率的结果不可靠。最小压降模型是指当管内压降梯度最小时，摩阻损失由重力压降向摩阻压降转变的时机下，管内积液最小，Belt[10]、Fan 等[11]均支持该模型。综上，后续通过最小压降梯度模型确定临界携液流速。

对某气田的管道倾角进行统计分析，发现倾角基本分布在0°～30°，当气液流经下倾管段时，重力作用将加速液相流动，形成分层流，下倾管段的持液率较低，因此积液主要分布在低洼上坡管段，故后续研究对象以上倾管段为主。在OLGA 软件中建立上倾管段模型，管道水平长度1 km，通过改变天然气质量流量，确定井口温度、系统压力、管径、上倾角、含水率、管壁粗糙度等因素下的临界携液流速，气质组分见表1。

表1 气质组分摩尔分数 单位：%

实验条件（见表2）与现场工况一致，表2 中的红色加粗字体为单因素分析中的固定因素。

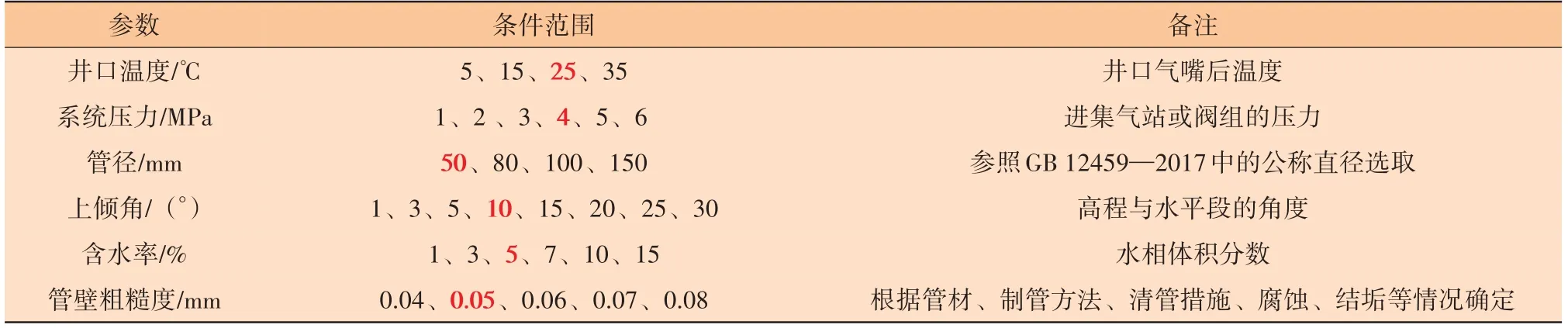
表2 实验条件

在固定因素下，应用双流体模型对上倾管段进行水力和热力计算，该模型的核心是求解质量守恒、动量守恒和能量守恒的微分方程，进而获得闭合剪切应力、局部流速和流型等瞬态流动特性，据此查看不同气量下的压降梯度和持液率变化，见图1。两相流动的总压降由加速压降、重力压降和摩擦压降组成，其中加速压降与其余两项相比，可以忽略不计。在气量较小时，液相所受的重力分量和液相与管壁的摩擦力之和大于气相曳力，气相流速难以克服阻力影响将液相从低洼处携出，此时管内重力压降占主导地位；随着气量的进一步增大，气相流速产生的曳力足以克服阻力，液层产生的波纹变稠密，上倾段液相平铺长度增加，液相回流量减少，直到液相不再回流，流动方向与气相流动方向相同，此时管内的总压降梯度降至最小，压降仍以重力压降为主，但摩擦压降的比重逐渐上升；之后，气相流量继续增大，液相逐渐被带出上倾管段，管内持液率继续下降，下降程度较之前有所减缓，说明要想让管内的积液达到完全排出的程度需要较大的气相流速，此时总压降逐渐增大。以上模拟结果也从侧面证明了采用最小持液率模型判断临界携液流速具有较强的保守性，最小压降梯度对应的气体流量为1 290 kg/h，临界携液流速为3.57 m/s。

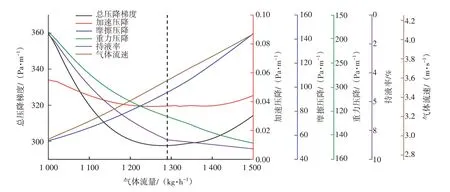
图1 上倾管段不同气量下的压降梯度和持液率变化

2 单因素影响分析

2.1 系统压力和井口温度

在表2 给出的条件下，分析系统压力和井口温度变化对临界携液流速的影响，见图2。在温度一定的条件下，系统压力对液相的影响较小，根据气体状态方程，系统压力与气相密度呈正比，压力越大，气相密度越大，气液两相间的摩擦、碰撞和剪切作用增强，气体携液能力增强，临界携液流速变小，但降低幅度逐渐减小，两者呈幂函数关系。在压力一定的条件下，井口温度增加，气相和液相黏度降低，但温度对液相黏度的影响更大，导致气体可携带的液膜厚度变小，气体携液能力变弱，临界携液流速变大，两者呈线性正相关。

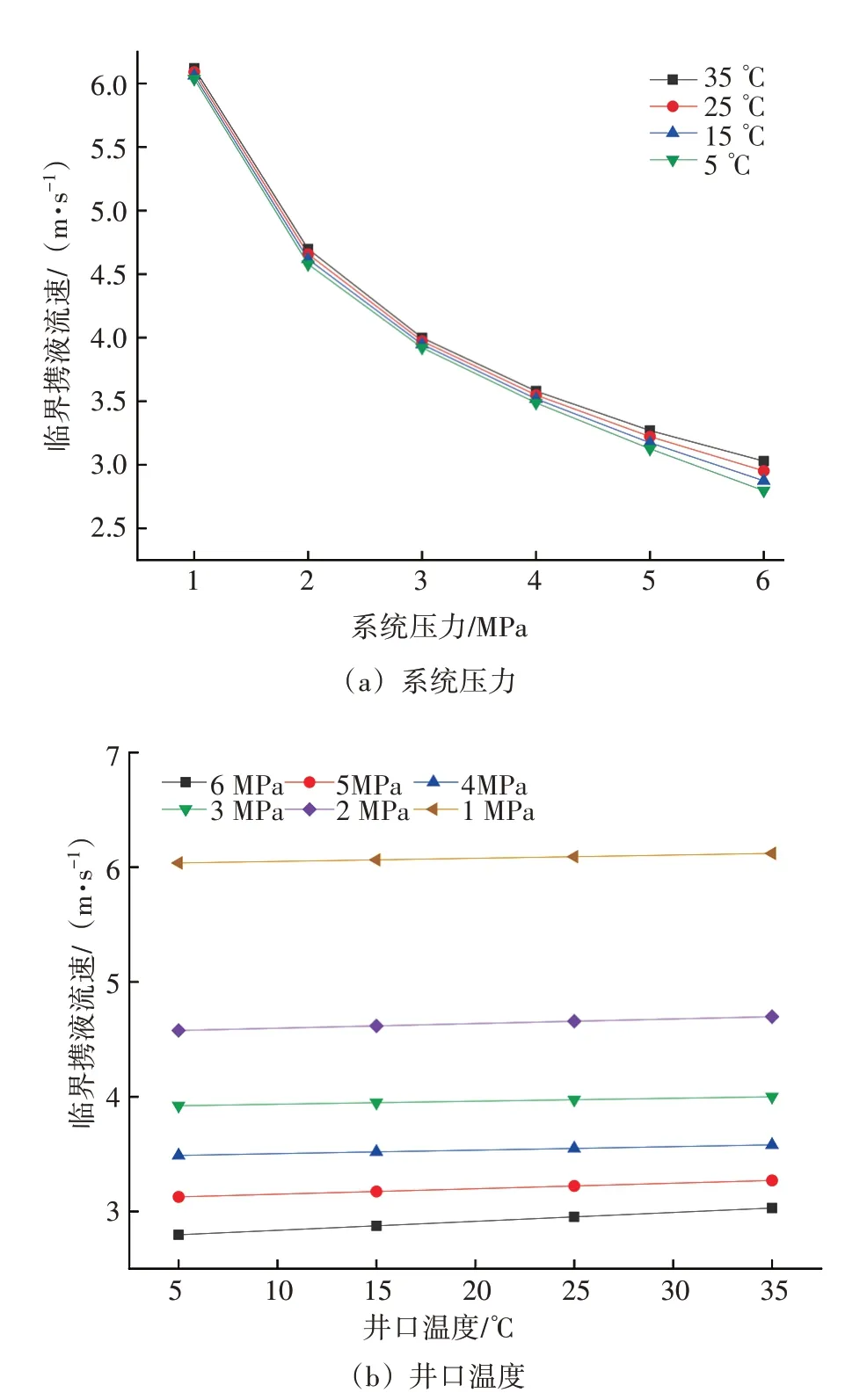
图2 系统压力和井口温度变化对临界携液流速的影响

2.2 管径和倾角

在表2 的条件下，分析管径和倾角变化对临界携液流速的影响，见图3。随着管径增大，气液流动面积增大，两相之间的剪切作用减弱，为达到之前的携液效果，需增大临界携液流速，两者呈线性正相关。随着倾角增大，积液在上倾管段受到的重力分量不断增大，持液率减小，此时气体要达到之前的局部流速需提高气体流速，且液膜沿管道内壁周向的分布更加均匀，综合作用下气体携液所需的能量增加，临界携液流速呈先快速增加后缓慢增加，两者呈对数关系。这与Belfroid等[12]提出的临界携液气速与管道倾角呈正弦分布的结果基本一致（文献中的倾角范围为0°～90°）。

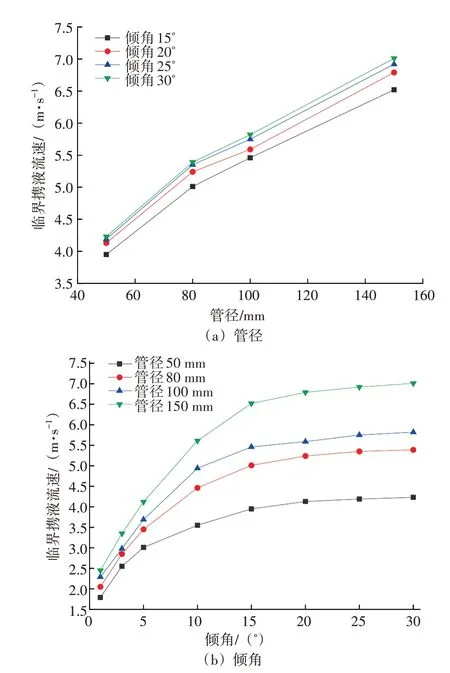
图3 管径和倾角变化对临界携液流速的影响

2.3 含水率和管壁粗糙度

在表2 的条件下，分析含水率和管壁粗糙度对临界携液流速的影响，见图4。随着体积含水率的增加，管内游离水和凝析液的含量增加，临界携液流速增大，但在含水率超过10%之后，临界携液流速的变化变小。以倾角10°为例，临界携液流速与含水率呈对数关系。随着管壁粗糙度的增加，气壁和液壁之间的剪切应用也增大，使积液变得困难，临界携液流速减小，两者呈线性负相关。此外，结合图3、图4，在相同的管径、含水率和管壁粗糙度的情况下，倾角越大，临界携液流速的变化越小，倾角大于20°时，其余因素对临界携液流速的影响较小。

图4 含水率和管壁粗糙度变化对临界携液流速的影响

3 交互作用影响分析

以上倾角因素的8 个水平为基础对其余因素的水平进行扩充，形成6 因素、8 水平的均匀实验设计，以此获取不同因素之间的交互作用强度。考虑到每次的实验设计表头形式不一，通过多次迭代，取各项偏差最小的实验方案，最终中心化偏差为0.271 7，L2偏差为0.033 0，修正偏差为0.420 4，可卷偏差为0.552 4，实验结果见表3。

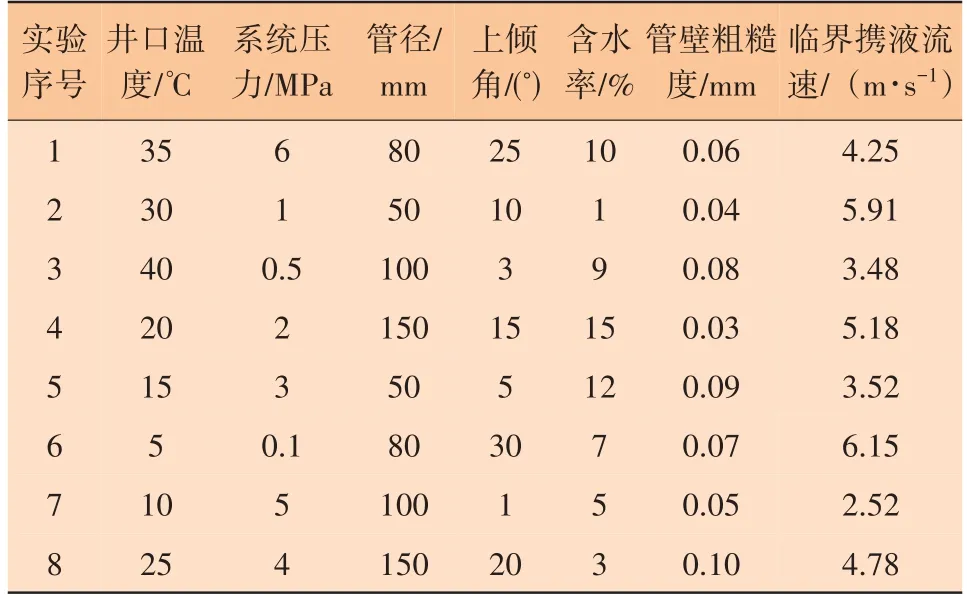
表3 实验结果

通过不断增加变量，对模型进行二次多项式逐步回归，得到的二次模型中F值为15 838.73，p值为0.006 1，调整后的相关系数为0.999 89，说明均匀实验设计方案合理，结果具有可信性。偏回归系数的检验结果见表4，t检验的绝对值越大，则该因素越重要。单因素中上倾角对临界携液流速的影响最大，其次为含水率和系统压力，其余未展示因素对临界携液流速的影响不显著；二次项因素中，系统压力和上倾角的交互作用最强，其次为管径和含水率的交互作用；表4中的p值均小于0.01，说明所列因素对结果的影响极其显著。

表4 偏回归系数的检验结果

4 模型建立与数据预测

以往以液泛经验公式为基础的优化模型通常只考虑气液表观流速、倾角和气液密度等对临界携液流速的影响，但从前述分析可知，影响因素之间还存在较强的交互作用，因此以往模型从机理上不具备广泛适用性。在此，采用基于集群策略和改进决策树为基础的随机森林模型对本文第2、3 章的数据进行回归，共计148 组数据，按照8:2 的比例随机抽取形成训练集和预测集，数据量分别为118组和30组。首先，通过Bootstrap方式对训练集进行有放回的抽样，随机抽取{X1,X2,…,Xn}共n个样本集；其次，随机抽取m个特征变量作为当前决策树的分裂特征集（m小于等于原始特征变量数量）；最后，输出每棵决策树的回归结果，取均值得到最终结果。随机森林模型避免了数据不平衡或单一特征变量带来的过拟合现象，且降低了噪声对预测效果的影响，决策树的数量n和特征变量m对模型的泛化能力影响较大[13]。模型结构见图5，数据回归公式如下：

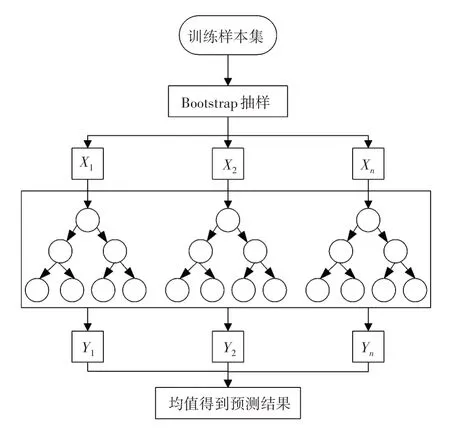
图5 随机森林的模型结构

式中：为回归平均估计，Xn为随机抽取的样本集，E为与Xn有关的期望，Θ为因变量。

以均方根误差（SRMSE）作为随机森林的误差估计值对n和m的数量进行调整，见图6。图6（a）中固定n=50，在m=3 时，训练样本的SRMSE最小为0.045 1 m/s；图6（b）中固定m=3，在n=150 时，训练样本的SRMSE最小为0.036 2 m/s。综上，确定在n=150、m=3的训练效果最好。

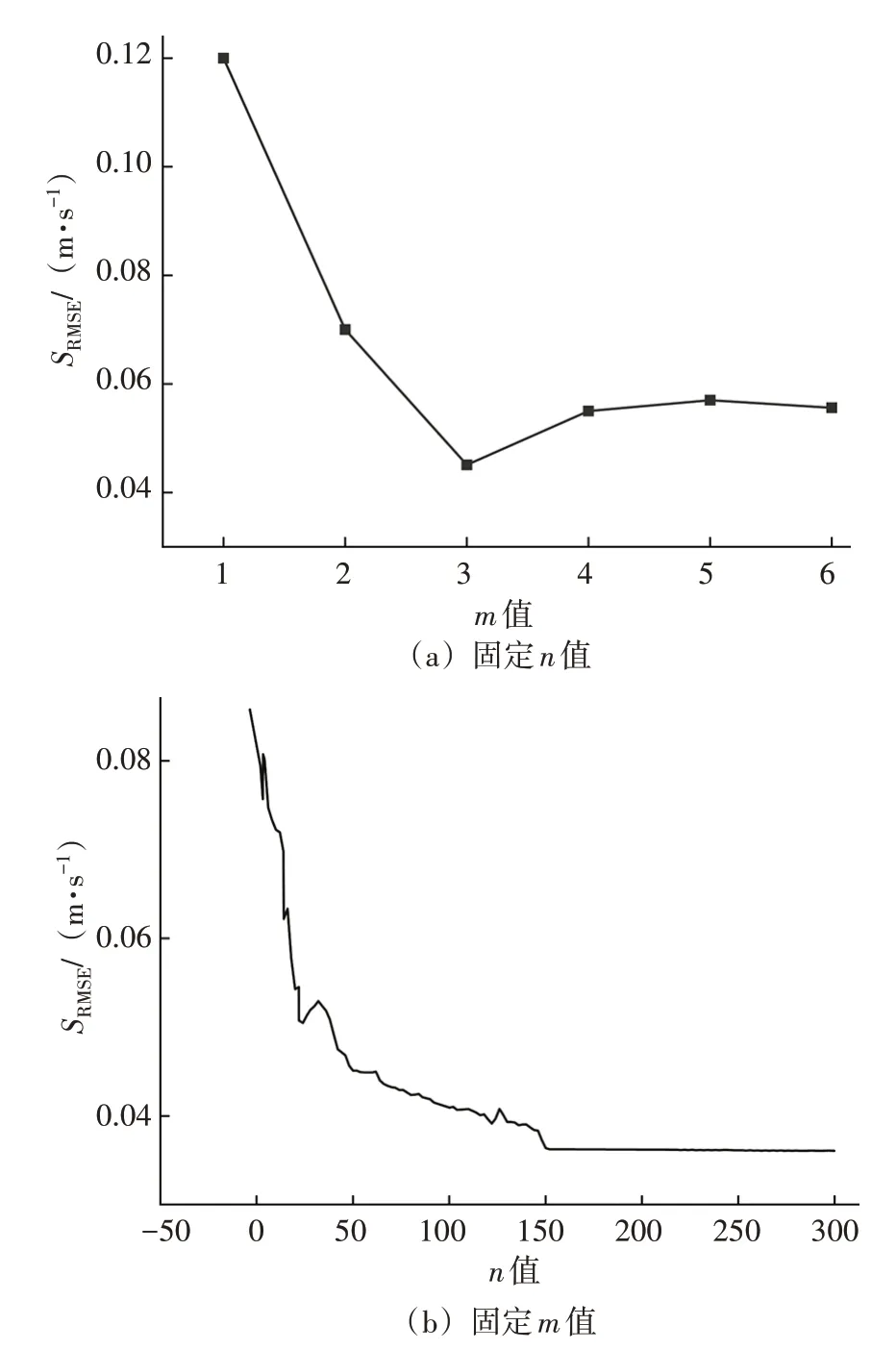
图6 超参数与SRMSE的关系

将数据代入训练好的随机森林模型，拟合结果和预测误差见图7。模型在训练集和预测集上的拟合程度较好，预测集的拟合优度（R2）并没有下降太多，说明模型具有较强的泛化能力和鲁棒性；预测结果的最大相对误差为7.87%，平均相对误差为2.08%，误差范围在气液混输管道工程实践的要求内，说明预测模型可以较好反映不同因素与临界携液流速之间的非线性关系。

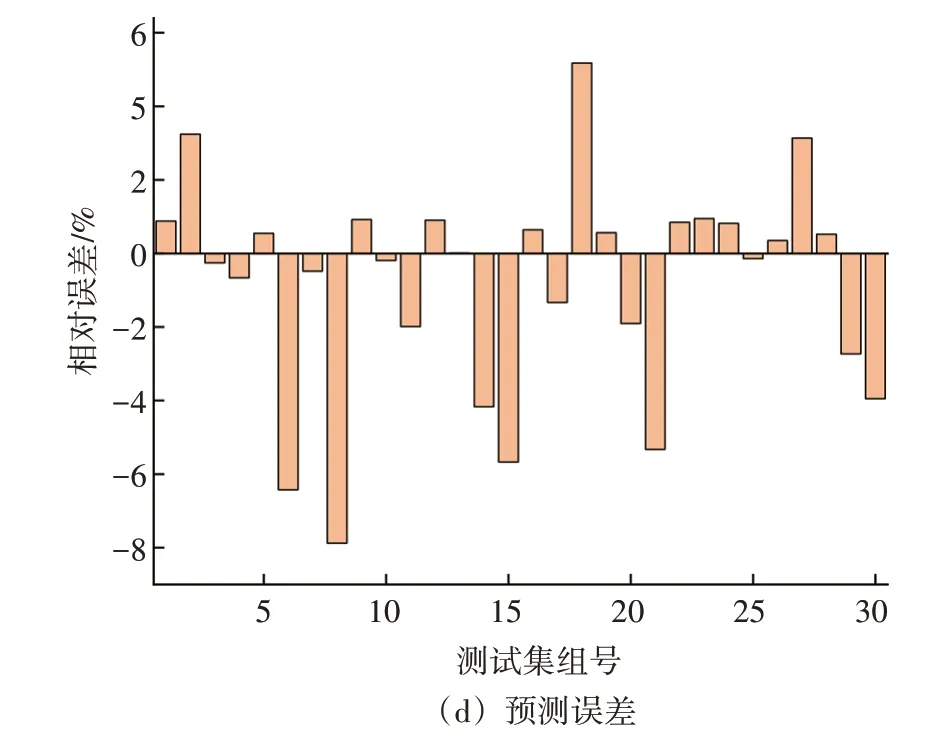
图7 拟合结果与预测误差

5 现场验证

将本文模型与陈建磊模型[4]、王旭模型[7]进行对比，考虑到现场实际管道高程不可能只具有单一的上坡段或下坡段，而是具有多起伏特性，故取不同上倾段临界携液流速的最大值作为模型值。同时，在现场通过控制井口气嘴压力，调节气体流量，将井口压力最小值对应的气速定义为临界携液流速的实际值（在此集输管道的出口压力固定）。取20口气井进行对比，结果见图8。

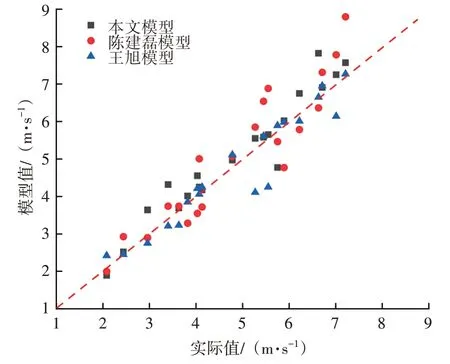
图8 不同模型的结果对比

如模型值大于实际值，则计算得到的临界携液流速可以指导现场实际，用模型值调整流速可以避免管道积液；反之，现场集输管道存在积液的可能性较大。本文模型有2 口气井出现了误判，模型符合率为90%；陈建磊模型、王旭模型分别有9 口、7 口气井出现了误判，模型符合率分别为55%、65%，这也再次证明了本文模型的科学性和适用性。

6 结论

1）通过最小压降梯度模型确定临界携液流速，压力与临界携液流速呈幂函数关系，温度、管径与临界携液流速呈线性正相关，含水率、上倾角与临界携液流速呈对数关系。

2）通过对均匀实验设计中的偏回归系数检验，单因素中上倾角对临界携液流速的影响最大，其次为含水率和系统压力；二次项因素中，系统压力和上倾角的交互作用最强。

3）通过优选决策树和特征变量建立随机森林模型，预测临界携液流速的最大相对误差为7.87%，平均相对误差为2.08%，现场验证结果的模型符合率为90%，证明该模型具有较强的适用性，可以用于指导现场生产。