高速低载频比传感信号下的逆变器有源阻尼自适应控制*

2024-03-06冯永芳

传感技术学报 2024年1期

冯永芳，白娜

(1.晋中职业技术学院电子信息系，山西晋中 030600；2.桂林电子科技大学海洋工程学院，广西桂林 536000)

并网逆变器是将电能输送到电力网络中的重要装置[1]，它的性能直接关系到整个电力系统的稳定。随着电网运行方式的改变，其产生的阻抗也会发生相应变化，在恶劣的电网环境下，逆变器控制中经常会遇到鲁棒性较差等困难，所以在这种情况下，使逆变器更加适应电网的运行已经成为电力系统需要面临的大问题。根据逆变器运行时的阻抗特点，控制有源阻尼，可以对逆变器的鲁棒性起到改善作用。

Kim 等[2]通过设计一阶观测器来估计电压导数，同时，通过稳定的零极点消除比例微分环路和有源阻尼部件的特定反馈增益结构，保证了从参考到输出电压的一阶闭环传递函数。以此实现了基于无电流传感器的升压变换器有源阻尼比例微分电压控制。Yeam 等[3]提出了一种新型滑模速度控制器，用于单逆变器双永磁同步电动机的并联运行。为了保证其稳定运行，通过主永磁同步电机的速度控制器和两台电机稳定运行的阻尼控制器联合控制电机参数，以优化阻尼振荡鲁棒控制性能。雷鹏娟等[4]为了解决滤波器的谐振问题，建立了一种基于滤波器的逆变器数学模型。该模型中的各项参数会对滤波器的谐振频率产生一定影响，根据滤波器的开关设置，分析了其在高频开关处的纹波衰减特性，并采用有源阻尼控制策略，将有源阻尼的极点布置在相应区域。根据逆变器系统的性质，对PI 调节器的参数进行设计，利用仿真软件分析了有源阻尼的控制方案，通过搭建仿真平台，验证了该控制策略能够有效控制逆变器系统。李臻等[5]以哈密尔顿系统为基础，建立了数学模型。通过陷波器的串联方式抑制了逆变器的最大谐振，将无源阻尼控制理论应用到逆变器控制中，避免并网系统受到外界干扰，结合仿真分析的方式，验证了该控制策略能够有效控制逆变器中的有源阻尼，可以有效降低系统的谐波失真。曹子恒等[6]提出了一种改进型电容电流反馈有源阻尼策略，解决了弱电网条件下、宽范围时变的电网阻抗导致的谐振频率变化问题。该方法加入了相位超前补偿环节，提升了逆变器有源阻尼的有效阻尼区。仿真结果表明，该策略具有良好的鲁棒性。

逆变器工作在高频运行和控制载波比低的情况下，存在谐振尖峰抑制，本文利用传感器获取高速低载频比后，利用传感信号对逆变器的有源阻尼进行了自适应控制，从而改善逆变系统的鲁棒性。

1 逆变器有源阻尼自适应控制技术设计

1.1 基于传感器信号采集的逆变器数学模型设计

在高速低载频比下，构建逆变器数学模型对系统的稳定运行十分重要，基于系统仿真模型的建立，本文以三相逆变器为研究对象，通过传感器装置采集高速低载频比的信号。并利用信号对其进行了数学建模。图1 给出了传感器采集信号的三相逆变器内部电路图。

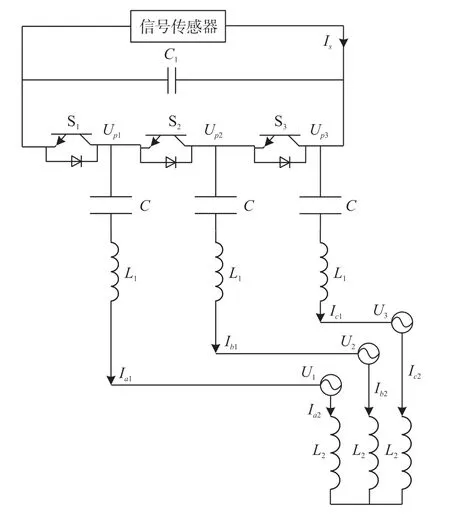
图1 三相逆变器电路图

图1 所示基于传感器采集信号的三相逆变器内部电路中，S1、S2、S3代表三相开关，Is代表直流侧的电流，L1为逆变器的电感[7]，Ia1、Ib1、Ic1代表三相逆变器的电流，Ia2、Ib2、Ic2表示电网的三相电流，C代表滤波电容，L2为电网的电感。根据三相逆变器的传感器电路原理，定义了逆变器运行的开关函数。利用该开关函数，建立直流电源与逆变器输出电压之间的关系[8]，将其表示为:

式中:Us代表直流侧的电压，Uz代表电网中性点与接地端的电压。

在高速低载频比传感信号下，逆变器运行时存在Up1＋Up2＋Up3＝0。逆变器在高速低载频比下会存在有源阻尼控制性能失稳的问题，根据对称原理[9]并结合运行电流的频域分析结果[10-11]，在高速低载频比下，建立逆变器数学模型，即:

以上根据三相逆变器的电路原理，定义了逆变器运行的开关函数、直流电源与逆变器输出电压之间的关系，在高速低载频比下，构建了逆变器数学模型。

1.2 分析逆变器有源阻尼机理

有源阻尼是逆变器反馈阻尼的一种常用方法[12]，在不考虑有源阻尼的控制延迟情况下，得到逆变器有源阻尼的反馈原理，其结构如图2 所示。

图2 逆变器有源阻尼的反馈原理

在原有逆变器有源阻尼反馈原理基础上，增加一个单相变压器，以避免电压过高或过低造成运行故障。同时，改变逆变器的连接方式，组成逆变器，增强阻尼效果。

图2 中，反馈系数λr在逆变器中起到增强阻尼的效果，在运行的逆变器中，输出电流Iu到电容电压Uc的传递函数为Fuc(s)，Fud(s)定义为输出电流Iu到定子电流Id之间的传递函数，表示为:

式中:j(2ωXs＋ωR)为逆变器的阻尼[13]，C为逆变器的电容，X为电抗，R为电阻，ω为转速，j 为虚数，jωX为继电器部分的阻尼。

考虑到控制延迟的存在，将逆变器的有源阻尼变换成双闭环的形式[14]，构建了电压反馈闭环传递函数，表示为:

式中:Ik表示电流闭环，Uk为电压闭环，Huc(z)为交流侧开环。

当反馈系数λr低于0.4 时，可以抑制逆变器的最大谐振，根据逆变器有源阻尼的反馈原理[15]，可以将逆变器的有源阻尼等效成一个控制电压环，避免影响逆变器有源阻尼的电流环性能。

1.3 传感信号约束下的逆变器有源阻尼自适应控制

基于逆变器有源阻尼机理的分析结果，引入高通滤波器，将滤波后的传感信号提供给逆变器[16]，作为约束条件。为了保证电网中电感变化的稳定性，针对高通滤波器建立了函数表达式，表示为:

式中:ϑrc(s)表示高通滤波器滤波传感信号后产生振荡阻尼的增益，S代表有源阻尼的安全裕度[17]，frc表示高通滤波器停止振荡阻尼产生的频率，通常用于补偿逆变器谐振频率周围的相位滞后问题。

在逆变器有源阻尼自适应控制策略中，利用低载频传感控制器MD 对逆变器的有源阻尼进行控制，避免系统存在稳态误差[18]，那么低载频传感控制器MD 在控制逆变器有源阻尼中的传递函数为:

式中:φp表示低载频控制器MD 的比例增益，fl表示谐振频率，φr表示谐振增益。

为了对高速低负载频比传感信号下的逆变器有源阻尼进行动态响应的研究，通过对其参数的调节，得出了逆变器的输出电压Uc与电网电感电流Ig之间的转换函数，以及Uc与滤波器电容电流Ir之间的转换函数，表达式为:

在高速低载频比传感信号下，根据式(8)和式(9)的传递函数，利用逆变器瞬态直接电流的控制[19]，制定了逆变器有源阻尼自适应控制策略，如图3 所示。

图3 逆变器有源阻尼自适应控制策略

对于大部分逆变器，有源阻尼控制时通常采用的都是高通滤波器，即利用高通滤波器对逆变器输出电压等引起的谐振进行控制，但是由于高通滤波器固有谐振特性以及数字控制延时会影响逆变器的运行稳定性，为此，图3 中，本文方法应用下的逆变器有源阻尼自适应控制策略如下:在采用高通滤波器为逆变器提供振荡阻尼的基础上，将其作为后续有源阻尼控制的约束条件，同时引入低载频控制器消除传感器的误差。在控制时，分别由正弦函数和余弦函数处理逆变器输出的电压，并输出谐振增益和低载频控制器的比例增益后，通过调整有源阻尼自适应控制回路的参数，实现了逆变器有源阻尼的自适应控制。

2 实验分析

根据1.3 部分正弦函数和余弦函数的处理结果，输出谐振增益和低载频控制器的比例增益后通过调整回路参数，实现逆变器有源阻尼自适应控制。为了验证所提方法有效性，设计下述实验。

2.1 测试设置

参与实验用的逆变器中，传感器采用MMA7361。如图4 所示。

图4 传感器的选择

主电路采用H 桥，使用IR2104 半桥驱动内置630 ns 死区，上管采用自举电容浮地驱动。SPWM 采用STM32F103C8T6 产生两路互补的30 kHz 的SPWM。LC 滤波器的截止频率约为开关频率的1/10～1/5，文章选用的是30 kHz 的开关频率，则LC滤波器的截止频率约为3 kHz。电流传感检测采用ACS712，该芯片可以直接测DC 电流和AC 电流，适合于对精度要求不高的场合，电压检测利用全桥整流，后经电压分压。稳压管是为了保护单片机AD 转换输入口的电压，将其钳位在3 V 以下。SPWM 产生使用单片机查表产生。正弦表计算时要注意ARR 寄存器的最大值和最小值。由于单片机的自动重装载寄存器ARR 是无符号二进制，由于单片机中的自动重装载寄存器ARR 是无符号二进制数，因此，正弦表的值需要进行0.5ARR 的偏移。当占空比大于0.5 输出为正，当占空比小于0.5 输出为负。PWM 的开关频率要大于15 kHz，本文用的是30 kHz。通过定时器中断来更新比较寄存器CCR 的值，以使PWM 的脉宽按正弦规律变化。实验测试如图5 所示。

图5 实验测试图

为了保证实验的有效性，预先对MMA7361 传感器采集精度进行测试。在采样频率为6.4f、5.9f、3.8f、2.6f以及1.7f下，对MMA7361 传感器对高速低载频比信号的采集误差进行统计和分析，结果如表1 所示。

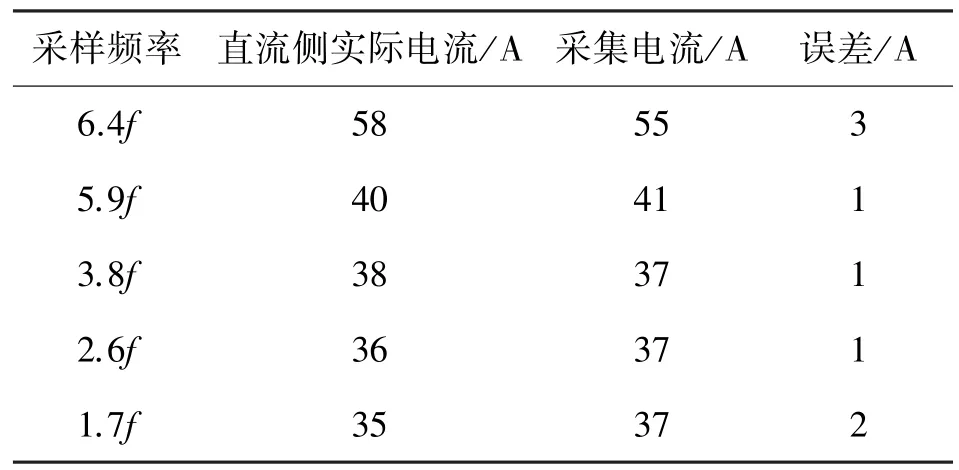
表1 高速低载频比信号的采集误差

分析表1 可知，采用MMA7361 传感器对高速低载频比信号的采集误差低于3 A，因此说明该传感器具有较好的采集精度。同时在5.9f、3.8f、2.6f时的采集误差低于1 A，因此将其作为下文稳定裕度测试和控制效果测试的基础参数设置。

2.2 稳定裕度对比

考虑到相位超前滤波器不适用于逆变器的电流反馈控制中，因此本文对比分析了采用LCL 滤波器的控制技术(文献[3])、应用于光伏发电并网逆变器的控制技术(文献[4])和所提控制技术对并网系统稳定裕度的影响情况。实际的逆变器参数如下:

逆变器的基波频率f1:65 Hz

滤波电容C:15 μF

逆变器的电感:2.02 mH

电网侧的电感L2:1.41 mH

滤波器的谐振频率f:2.0 kHz

电网电压的有效值:220 V

根据以上参数，利用仿真软件分析了采用LCL滤波器的控制技术、应用于光伏发电并网逆变器的控制技术和所提控制技术时，并网系统的稳定裕度，结果如表2～表4 所示。

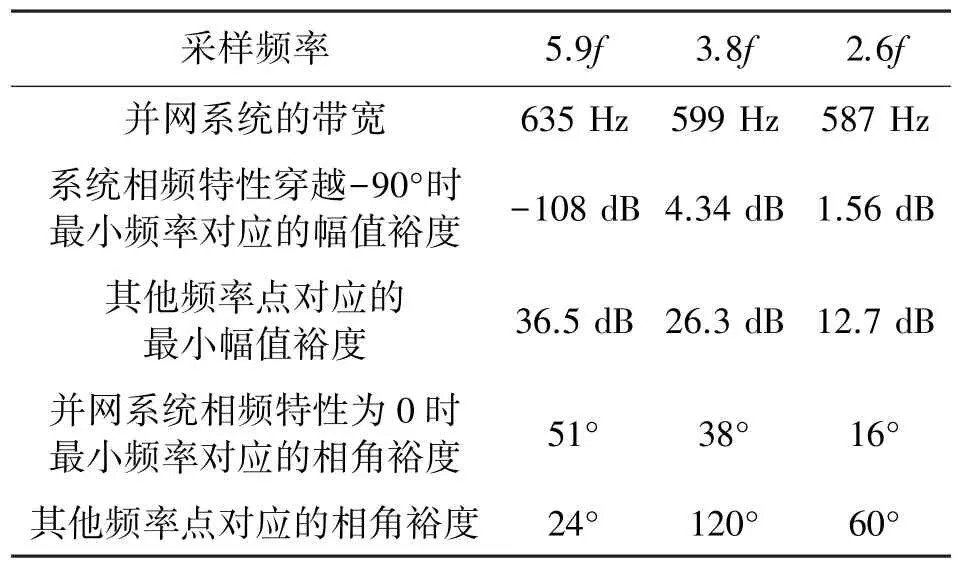
表2 采用LCL 滤波器的控制技术

从表2 的结果可以看出，采用基于LCL 滤波器的控制技术时，较高的采样频率会影响系统的稳定性，造成系统的稳定性变差，而且系统相频特性穿越-90°时最小频率对应的幅值裕度小于0，变化幅度为109.56 dB。随着采样频率的降低，系统逐渐趋近稳定。

表3 中，采用应用于光伏发电并网逆变器的控制技术之后，在较高的采样频率下系统比较稳定，系统相频特性穿越-90°时最小频率对应的幅值裕度由2.43 dB 下降至0.30 dB，变化幅度为2.13 dB。但是当采样频率降低时，系统的稳定裕度开始变小，说明在应用于光伏发电并网逆变器的控制技术下，原本稳定的系统也会失去稳定性。

表3 应用于光伏发电并网逆变器的控制技术

表4 中，采用所提控制技术之后，在任意采样频率下，系统的稳定性都很好，系统相频特性穿越-90°时最小频率对应的幅值裕度由2.46 dB 下降至1.18 dB，变化幅度为1.28 dB，相较于两种对比控制技术，变化幅度较小，说明所提的控制技术可以将系统控制在原有的稳定裕度下，保证系统稳定运行。

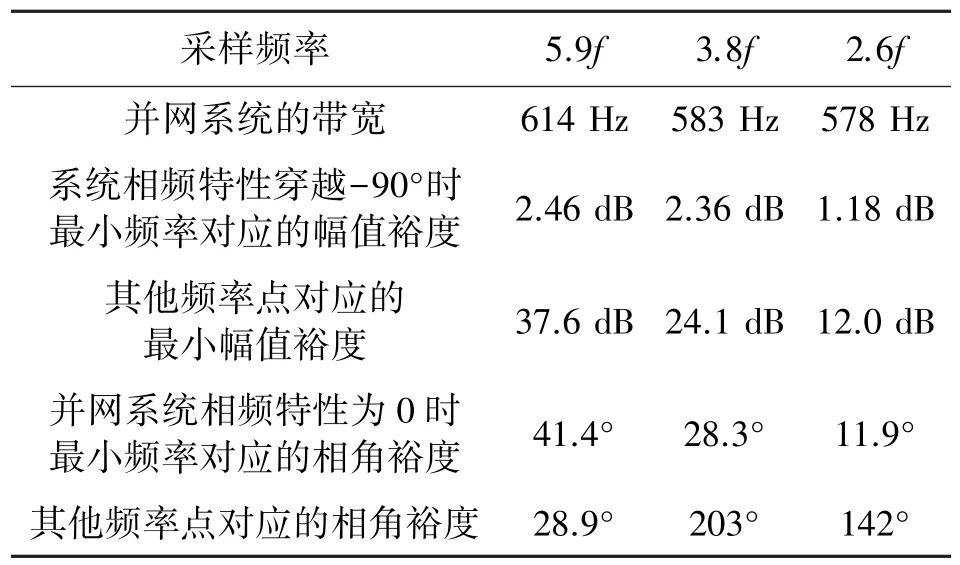
表4 所提控制技术

综合以上分析，发现所提控制技术可以保证系统运行的稳定性。

2.3 控制效果分析

通过稳定裕度的对比，发现所提控制技术在逆变器有源阻尼自适应控制中的适用性更好，可以使系统在各个采样频率下处于稳定，那么采用所提控制技术对逆变器的有源阻尼进行控制，在不同的采样频率下，得到了电网电压与并网电流之间的波形图，如图6 所示。

图6 电网电压与并网电流的波形

根据图6 的结果可知，采用所提控制技术在不同采样频率下，系统的并网功能可以正常实现，并且输出的并网电流与电网电压具有相同的相位和频率。在采样频率为5.9f时，输出并网电流和电压均表现为正弦状态，波动范围分别为[35 A，58 A]和[185 V，225 V]。在采样频率为3.8f和2.6f时，输出并网电流和电压出现不同程度的异常增长或降低，但整体相同的相位和频率趋势一致。同时，在采样频率为3.8f和2.6f时，输出并网电流和电压波动范围分别为[-30 A，55 A]和[185 V，225 V]、[-30 A，58 A]和[185 V，225 V]，只有电流产生了较大的波动，但整体趋势与5.9f时一致，其主要原因可能是通过逆变器的电流受周边环境的干扰产生了较大波动。说明采用所提控制技术具有较好的控制效果，控制后的电压波动范围在[185 V，225 V]之间，进一步确保了系统运行的稳定性。其主要原因是所提控制技术利用电流到电容电压与定子电流之间的传递函数，将逆变器的有源阻尼等效为控制电压环，优化了并网电压和电流的控制效果。

2.4 控制性能测试

为了进一步验证所提出逆变器有源阻尼自适应控制性能，在同一采样频率3.8f下，分别测试利用所提控制技术前后的电压波形图，如图7 所示。

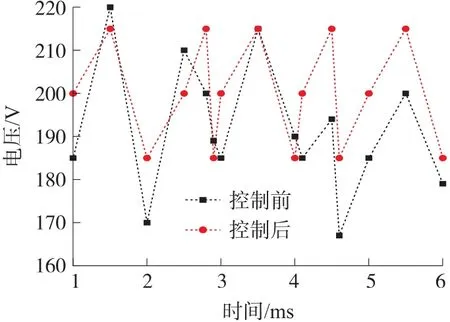
图7 所提控制技术前后的电压波形

分析图7 可知，采用所提控制技术前，电压波形出现了极大值220 V 和极小值168 V，且波动范围较大。而采用所提控制技术后的电压波形范围较稳定，在[185 V，215 V]之间波动，最大电压和最小电压分别为215 V 和185 V。经对比可知，所提控制技术控制后，电压波动范围由[168 V，220 V]稳定至[185 V，215 V]，具有更好的控制效果，其主要原因是所提控制技术基于高速低载频比传感信号建立了逆变器数学模型，获取了较好的阻尼分析结果，进一步优化了电压控制性能。