利用机器学习模拟湿物理参数化方案*

陈锦鹏 冯业荣 黄奕丹 蔡乐天 洪晓湘 文秋实

1 引 言

数值天气预报模式涉及许多复杂的物理过程，例如湍流边界层过程、次网格积云对流过程、云微物理过程以及云和气溶胶辐射过程等。这些物理过程往往与网格不可分辨的大气过程密切关联，因此模式中采用参数化方式处理（徐道生等，2014）。由于参数化方案通常基于有限观测试验和简化的理论进行构造，包含大量半经验半理论数学关系式和不完全确定的经验参数，故并不总是与自然界的客观情况一致，例如某些湿物理参数化方案针对地域特征明显的局地强降水的预报能力明显不足（Han，et al，2016；杨扬等，2021；陈黛雅等，2023）。另外，参数化方案越复杂，非闭合问题就越凸出（Pan，et al，1998），从而导致所需的变量维度越大、主观经验常数越多，不仅计算量大，而且结果存在较大的不确定性。

为克服传统参数化方案存在的问题，近年来许多研究人员利用机器学习方法模拟参数化过程。Chevallier 等（2000）利用多层感知器网络模拟大气长波辐射传输方案取得进展，并成功应用到欧洲中期天气预报中心的全球模式。随后更多的机器学习模型被应用于各种参数化方案，有效地模拟了模式中的非绝热加热、热带对流和辐射过程（Krasnopolsky，et al，2010；Brenowitz，et al，2018；Gentine，et al，2018；Rasp，et al，2018）。O'Gorman 等（2018）基于常规参数化方案的数据训练随机森林模型并应用于大气环流模式，很好地模拟了对流云与大尺度环境的相互作用，准确捕捉了降水的气候特征及降水极值。Han 等（2020）针对湿物理过程利用深度卷积残差神经网络（ResNet）结合恒等快捷连接（identity shortcuts），同时在代价函数中引入湿静力能守恒约束，得到的机器学习参数化模型给出了积云非绝热过程引起的温度倾向和水汽倾向以及云水、云冰信息，显示出很好的模拟效果。

在诸多物理过程中，与云相关的湿物理过程（云微物理和积云对流）对模式降水预报有很大影响。湿物理过程的总效应是在模式预报方程组中起热源和水汽汇的作用，即通过水汽相变和对流活动在模式网格点上产生温度倾向（加热或冷却）和水汽倾向（增湿或干燥）（Yanai，et al，1973；Arakawa，et al，1974；Pan，et al，1998；Hong，et al，2006）。传统参数化方案被设计成理想化的上下运动的单柱模型（Song，et al，2011），实际对流和云雨活动极其复杂（Ghan，et al，2000；Marsham，et al，2006），且与地域和大气背景条件紧密关联（冯业荣等，1997；Xie，et al，2010；Zhang，et al，2021）。为了探究机器学习算法对湿物理效应的模拟潜力，文中采用4 种机器学习算法，即基于决策树的梯度提升算法（LightGBM）、全连接神经网络（FC）、卷积神经网络（CNN）和卷积块注意力模块（CBAM）开展湿物理参数化方案模拟研究。根据模式动力框架特点及变量空间分布，从数值预报业务实际出发设计基于“像素学习”的机器学习模型，以检验机器学习算法在模拟湿物理过程中的有效性，为进一步构建实时在线湿物理参数化方案提供研究基础。

2 研究数据生成

选取2015 年10 月2 日台风“彩虹”作为研究个例，利用华南区域气象中心的台风业务数值预报模式（CMA-TRAMS）产生数据集。CMA-TRAMS是基于CMA 模式框架开发的区域数值预报业务系统。文中模拟范围取（12°—24°N，105°—123°E），水平分辨率 0.12°×0.12°，网格数为101×151，垂直方向67 层。模式顶高 30 km。取 ECMWF 全球预报模式 IFS 资料作模式初、边值，以10 月 2 日 12 时（世界时，下同）为模式初始时刻，积分5 h。模式基本预报量包括纬向风（u）、经向风（v）、垂直速度（w）、无量纲气压（Π）、比湿（q）和位温（θ）等。

对CMA 模式框架来说，湿物理效应体现在位温预报方程右端的热源项和水汽预报方程右端的水汽汇汇本研究开展两组试验。试验1 采用湿模式，保留与当前业务模式一致的全套物理参数化方案（陈子通等，2020）。试验2采用干模式，关闭试验1 中的云微物理方案（WSM6）和对流参数化方案（NSAS），其他物理选项保留与试验1 相同。因此，针对位温和比湿比较干、湿模式的差异可反映湿物理参数化方案的作用。为了生成机器学习所需要的数据集，同时使用干、湿模式冷启动积分第1 小时的数据构建训练集和验证集，使用后续积分第2 到第5 小时产生的数据作为测试集。

3 机器学习模型设计

3.1 输入特征构造

在CMA 模式的动力框架中，变量的空间分布水平方向采用Arakawa C 网格，垂直方向采用Chaney-Phillips 跳层。时间积分采用半隐式半拉格朗日方案，下一时刻的状态是由当前及过去一个时刻的状态通过求解亥姆赫兹方程确定（薛纪善等，2008）。

式（1）为亥姆赫兹方程，计算模板数据点是19 个。每个格点与其周围18 个格点的变量构成一个亥姆赫兹方程。19 个系数中，中心点的系数（B1）及其上、下相邻点（B10和B15）的系数比其他格点的系数至少大1 个数量级。方程系数B1—B19的空间分布如图1 所示。

图1 三维亥姆赫兹方程系数分布示意Fig. 1 Schematic distribution of coefficients in the threedimensional Helmholtz equation

另外，物理过程参数化方案也是逐点计算的，其数值主要由环境变量在该网格点及其周围有限点的状态决定。因此，在有限的积分时间内无论是模式动力框架或是物理参数化，变量的未来状态主要由当前计算格点周围的局部状态所主导。从这样的观点出发，以局部采样的统计视角进行建模。机器学习模型的输入特征（feature）取CMA 模式基本预报变量，即u、v、w、Π、q、θ这6 个要素。设在网格点P（i,j,k）由湿物理参数化方案产生的变量倾向为（文中指和），机器学习模型参数为Θ，则假设存在如下形式的模型映射关系

式（2）中向量X=（u,v,w,Π,q,θ）代表模式变量，只取网格点P（i,j,k）周围有限的网格点。机器学习模型的目的是依据当前时刻环境变量X估计湿物理过程引起的位温和湿度倾向。现阶段由于主要考虑在短时临近模式中的应用，因此利用第1 小时预报时效（1 h）的数据集对模型进行训练和调参，挖掘潜在的映射关系，再应用后续2—5 h 时效的数据集对模型进行测试。

文中把水平气象要素场表示为2D 图像、把经过垂直方向信息压缩的不同要素种类表示为1D 通道，具体为：在输入模型前，对每个要素预报场在垂直方向上做邻近层次的加权平均采样，即对于数据集中某一点的输入要素xi,j,k，做如下变换

为了方便引入集成学习模型和深度学习模型，将处理后的输入特征构造为两种特定的形式：一种称为“线特征”，即以P点为中心边长为L的正方形区域进行采样，6 个要素的采样数据按照一定顺序连接成一维向量，如图2a 所示。另一种称为“体特征”，类似三维图像数据，将6 种要素的同层（对于Chaney-Phillips 跳 层，u、v、w和 Π 是 一 层，q和 θ是另一层，两层紧邻）水平采样作为“通道”叠加起来，以P点为例，其对应的输入特征如图2b 所示。

图2 不同机器学习模型的特征输入示意Fig. 2 Conceptual diagrams for line and volumetric feature inputs in different machine learning architectures

两种采样处理中P均为矩形采样区域的中心点。对比来看，“线特征”失去了空间分布上的关联信息，而“体特征”仍可以保留空间分布的关联性。

3.2 建模方案

本研究采用两类建模算法—集成学习和深度学习。其中集成学习选用兼顾效率和精度的代表性算法LightGBM（简称LGB）（Ke，et al，2017），它是在梯度提升决策树算法基础上引入多项优化技术进行改进和提升的一种算法框架，擅长二维数据（列为特征、行为样本）建模。深度学习模型选用3 种代表性神经网络结构，从简单到复杂分别为全连接神经网络（简称FC，图3a）、LeNet5 范式的卷积神经网络（简称CNN，图3b）（Lecun，et al，1998）、卷积块注意力模块（Convolutional Block Attention Module，简称CBAM，图3c）（Woo，et al，2018）。FC 输入与LightGBM 相似的二维数据，CNN 加入了可自动提取多通道图像信息（三维数据）的卷积层和池化层组合。CBAM 是在CNN 基础上加入通道注意力和空间注意力的结合模块，能够自动调整每个通道和每个水平格点的权重。因此，LGB 和FC 采用“线特征”输入，CNN 和CBAM 采用“体特征”输入。

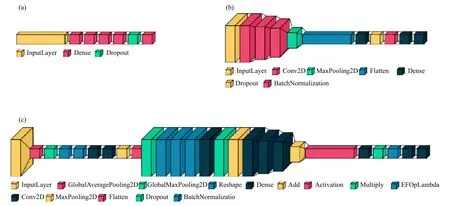
图3 三种深度学习模型结构示意 （a. FC：全连接神经网络，b. CNN：卷积神经网络，c. CBAM：卷积块注意力模块）Fig. 3 Structural diagrams for three deep learning networks （a. FC：fully-connected neural network， b. CNN：convolutional neural network，c. CBAM：convolutional block attention module）

所有的机器学习模型均采用归一化法对输入特征进行预处理。从矩形采样区域边长的角度来看，为避免“线特征”过长造成冗余，对于LGB 和FC 模型选取边长L=15 的格点采样区域组成“线特征”（即特征数为15×15×6=1350）；而CNN 和CBAM具有较好的自动提取特征能力，选取边长L=19 的格点采样区域组成“体特征”（即特征数为19×19×6=2166）。

湿物理过程主要在对流层发挥作用，本试验针对层次索引为9—30 的对流层（对应高度1—10 km），以湿物理参数化方案产生的比湿倾向和位温倾向作为研究对象。为了最大限度捕捉各输入特征的分层信息，对和均采用逐层独立建模。

为了尽可能地模拟短时临近模式的实际业务环境，逐层次建模方案为：以预报时效1 h 的数据集作为训练集和验证集，在4 折交叉验证的框架中进行建模和调参，增强模型稳定性和多样性；以预报时效2—5 h 的数据集作为测试集，最大限度地测试模型面对发生数据漂移（data drift）的数据集的泛化能力。表1 显示各类数据集的样本数量，其中测试集是指逐时样本数。训练集和验证集样本数之和等于测试集，满足模型训练和测试需求。

表1 不同机器学习模型的样本大小Table 1 Sample sizes of different machine learning models

4 试验结果

4.1 测试集检验指标

检验各类模型在测试集上的表现。首先算出干、湿模式（试验1 和试验2）的差值作为真值（训练的目标值），然后以各模型输出作为评估对象，计算两者间的平均绝对误差（MAE）。图4 是位温倾向的检验结果。尽管各类模型的构造不同，但MAE垂直分布形态非常相似，反映学习效果主要依赖数据内在的关系而非依赖于模型的类型。LGB 总体上优于其他3 类模型，其平均MAE 为0.2469 K/h，最差为FC 模型，平均MAE 为0.2739 K/h。所有模型在对流层上部和下部均优于中部，最小MAE 为LGB 模型和CNN 模型的0.17 K/h。各模型在对流层中层（17—19 层，即3800—4700 m 高度）均表现较差，其中FC 模型MAE 最大，达0.452 K/h，表明对流层中层模型映射规律偏弱，训练难度大。从时间上看，各模型的MAE 在各层上均随着预报时效延长逐渐增大，意味着测试集出现数据漂移，模型泛化能力不足。数据漂移可能是数值模式预报误差引起的，由于模式积分开始时需要一定时间使各要素间保持协调（即起转问题），故训练数据与预测数据的分布随时间发生偏移。

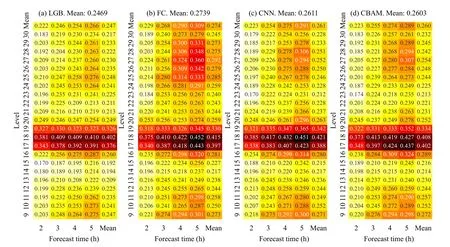
图4 位温倾向的平均绝对误差热力图 （单位：K/h）Fig. 4 Heatmaps for mean absolute error of potential temperature tendency （unit：K/h）

图5 给出测试集上比湿倾向q˙ 的MAE 热力图。大体上各模型表现相当，LGB 略优， MAE 平均为10.44×10-2g/（kg·h）；FC 模型最差，MAE 平均为11.37×10-2g/（kg·h）。各模型在对流层上部（17 层（3800 m）以上）均优于对流层下部（17 层以下）。与位温倾向（）不同的是，的明显误差不是在对流层中层而是在低层，其中FC 模型MAE 最大达24.88×10-2g/（kg·h），表明在对流层低层分布规律相对难以捕捉。随着预报时效延长，同样也存在数据漂移现象。

图5 同图4，但为比湿倾向 （单位：10-2 g/（kg·h））Fig. 5 As in Fig. 4 but for specific humidity tendency （unit：10-2 g/（kg·h））

4.2 大量级样本特征

文中研究的是中国南海台风过程。由台风对流活动产生的热源和水汽汇主要出现在台风中心附近，表现为湿物理过程产生的位温倾向（）和比湿倾向（）在台风区域量级较大，其他区域量级很小，因此测试集包含了大量和值量级极小（绝对值近乎为0）的样本。文中关心的是机器学习模型对大量级样本的拟合情况。为了更加直观地观察各层的大量级样本模拟情况，先对每层样本按数值从大到小顺序组成新的样本序列，然后对该层分别选取序列最前面和最后面各200 个样本，最后根据样本排序沿垂直方向进行平均。定义第j号样本沿垂直方向平均的真值Oj和平均的模型估计值Pj分别为

式中，m为总层数，Oij为第i层上序号为j的真值，为第i层上序号为j的模型输出值。样本序号取j=1，···，200 表示最前面200 个最大样本（正样本，简称O+200）；样本序号取j=n-199，···，n表示最后面200 个最小样本（负样本，简称O-200）。n为每层的样本总数。挑 选 预报时效为2 h 和5 h 的和测试集对正样本（O+200）和负样本（O-200）进行详细对比。

图6 预报时效2 h 垂直平均位温倾向前200 个最大样本和后200 个最小样本真实值与模型估计值对比 （a. LGB，b. FC，c.CNN，d. CBAM）Fig. 6 Comparisons between vertically averaged potential temperature tendencies from moist physics scheme （truth） and ML architectures for the top 200 maximum and bottom 200 minimum samples at the 2nd forecast hour （a. LGB，b. FC，c. CNN，d. CBAM）

图7 同图6，但为预报时效5 hFig. 7 As in Fig. 6 but for the 5th forecast hour

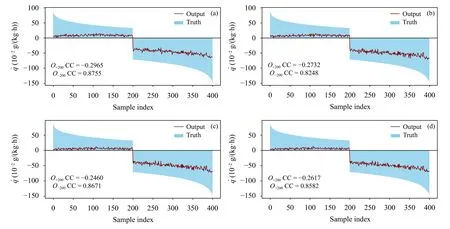
图8 同图6，但为比湿倾向 （） 测试集Fig. 8 As in Fig. 6 but for specific humidity tendency （）

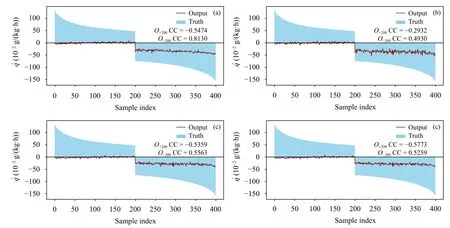
图9 同图8，但为预报时效5 hFig. 9 As in Fig. 8 but for the 5th forecast hour

4.3 水平结构分析

不难理解，天气系统不同，由湿物理过程产生的热源和水汽汇的水平分布也将不同。台风系统的云雨分布特征是围绕台风中心呈现典型螺旋结构。图10 给出预报时效2 h 各机器学习模型对26 层（7945 m）位温倾向的 模 拟 情 况。各模型（图10a—d）均成功模拟了台风热源结构的细节特征，对螺旋结构刻画非常准确，分布形态与真值（图10e）非常接近。台风中心的南侧有明显的加热（正值区），台风中心北侧热源弱。各模型输出的差异性很小，很好地捕捉到了台风的非对称“螺旋”模态。

图10 预报时效为2 h 第26 层 真值和各模型输出 （从a 至e 分别为LGB、FC、CNN、CBAM 和Truth）Fig. 10 Comparisons of potential temperature tendencies between “truth” and outputs from ML architectures on the 26th level at the 2nd forecast hour （from a to e： LGB，FC，CNN，CBAM and Truth）

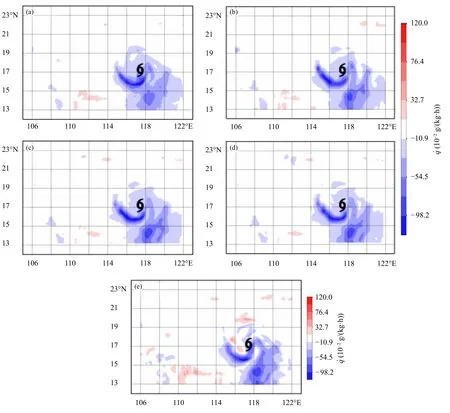
图11 同图10，但为比湿倾向 （）Fig. 11 As in Fig. 10 but for specific humidity tendency （）

图12 和13 显示各模型在第11 层（1645 m）分别 对和第2 h 的 测 试 情 况。与 真 值 相 比，4 类 模型能正确模拟台风热源和水汽汇正、负分布结构，但模拟强度明显偏弱，尤其是湿度倾向量级更弱，模拟效果明显不如26 层。

图12 同图10，但为第11 层Fig. 12 As in Fig. 10 but on the 11th level

图13 同图12，但为比湿倾向 （）Fig. 13 As in Fig. 12 but for specific humidity tendency （）

图14 给出预报时效2 h 各类模型在第18 层（4238 m）的模拟结果。可以看出，各模型输出的差异很小，但是与真值（图14e）相比，除了台风中心附近南侧两条较强的螺旋加热带外，其他部分的水平结构细节差异较大，这是导致该层平均MAE 较大（参见图4）的原因。该层温度在0—2℃，大气接近冻结的状态，同时存在多种水相态，湿物理过程比较复杂，不连续性较大，机器学习训练难度大，模型泛化能力不足。

图14 同图10，但是第18 层Fig. 14 As in Fig.10 but on the 18th level

5 结论与讨论

在数值天气预报模式中，湿物理参数化对降水预报有重要影响。湿物理参数化效应是在模式预报方程组右端作为热源和水汽汇发生作用，通过水汽相变和对流过程对网格点产生温度和水汽倾向。本研究利用机器学习方法模拟传统湿物理参数化方案的温、湿效应。针对中国南海台风过程，采用4 种机器学习算法，即基于决策树的梯度提升算法（LightGBM）、全连接神经网络（FC）、卷积神经网络（CNN）和卷积块注意力模块（CBAM）开展湿物理参数化模拟研究。将数值预报模式变量作为机器学习模型的输入特征，结合模式动力框架和变量空间分布特点，提取格点局部信息建模，针对湿物理参数化方案生成的数据集进行训练。

针对测试集的验证表明，4 种学习模型均能较好地模拟传统湿物理参数化方案的温、湿效应。在对流层上层，模拟的位温倾向（）和湿度倾向（）的水平分布与真值分布十分接近，各模型均较好地给出台风对流活动产生的加热（干燥）螺旋结构。对于垂直平均的大量级样本而言，各模型在测试集上偏向于估计正样本（热源），而在测试集上则偏向于估计负样本（水汽汇），模拟结果能反映台风整体作为大型深厚对流系统的潜热加热基本特征。尽管各类学习模型结构不同，但模拟结果大体相当，均能较好地发现输入特征与模拟变量的潜在映射关系，在数小时预报时效内对湿物理参数化方案均具有一定的模拟能力。无论是对于或是，LGB 模型均表现略优，平均绝对误差（MAE）最小。在 对 流 层 中 层的MAE 最 大，模 拟 的与 真 值比较，台风中心南半部较好，北半部较差。在对流层下层，模拟效果不如上层，表现为机器学习模型给出的和强度较弱，但是水平结构仍与真值相似。由于数据漂移的原因，各类模型的模拟能力均呈现随预报时效延长逐步下降的特点。由于湿物理参数化方案的开关性质和强非线性特征，局部信息建模可能存在一定的不足，例如在气温接近冰点，水多相态共存的对流层中部区域，的模拟误差较大。在水汽含量高的对流层低层，的模拟效果也有待改进。

本研究针对台风过程，由于训练数据较少，所得到的学习模型是否适用于台风以外的其他天气系统有待验证，后续可通过增加训练样本及迁移学习增强模型的适用性。另外，本研究以冷启动方式运行数值预报模式，受起转问题影响，模式变量需要一定时间才能达到彼此协调，由于训练数据直接从对比积分1 h 的干、湿模式得到，因此实际默认起转对湿物理参数化方案的影响很小，这一点是否合理需进一步分析评估。此外，虽然参数化方案是瞬间生效的，但其影响却是与模式大尺度动力过程紧密结合的，每次调用参数化方案产生的湿物理效应会随着模式动力过程向下游传播，对后续模式预报产生累加作用，因此较长时间的模式积分将使参数化方案和动力过程的影响互相交织，导致训练数据中掺杂动力因素带来的噪音，因此文中仅对模式积分开始数小时的数据进行训练和测试，一方面训练模型可适用于短时临近预报模式，另一方面也尽量减少动力过程对模型训练的干扰。从结果上看， 忽略起转问题并未对湿物理参数化方案的物理性质有显著影响。