城市轨道交通正交异性钢桥面板疲劳损伤系数研究
2024-03-05周新六向中富何孟松黄海东张兴健
曾 勇,周新六,向中富,何孟松,黄海东,马 虎,张兴健
(1.重庆交通大学 山区桥梁及隧道工程国家重点实验室,重庆 400074; 2.重庆市轨道交通(集团)有限公司,重庆 401120)
目前我国城市轨道交通已经进入了快速发展的新阶段。截至2022年底,我国已有55个城市开通了城市轨道交通线路,运营线路里程突破1万km[1-2]。由于采用公交化发车模式,城市轨道交通具有运营时间固定、发车频率高、发车车次多等特性[3-4]。城市轨道交通中的桥梁结构与荷载特性与公路桥梁[5]及铁路桥梁[6]均不同。正交异性钢桥面板的疲劳问题非常重要。学者针对正交异性钢桥面板结构疲劳开裂开展了大量研究,取得了丰硕的成果[7-12]。公路与铁路的正交异性钢桥面板结构设计已有相应的规范,但这些规范能否直接适用于城市轨道交通正交异性钢桥面板的结构设计还值得商榷。
城市轨道交通桥梁运营具有独特性,对其疲劳行为与性能评估的研究十分必要。本文开展了基于列车荷载作用频次的城市轨道交通正交异性钢桥面板的疲劳损伤系数的研究,对完善城市轨道交通正交异性钢桥面板的疲劳设计及规范的修订具有重要的意义。
1 城市轨道交通正交异性钢桥面板的疲劳验算现状
《城市轨道交通桥梁设计规范》(GB/T 51234—2017)[3](简称规范1)对城市轨道交通钢桥面板的疲劳评估有明确的规定。疲劳应力幅Δσp的计算式为
Δσp=|σp,max-σp,min|
(1)
式中:σp,max为最大应力(MPa),拉力为正,压力为负;σp,min为最小应力(MPa),拉力为正,压力为负。
疲劳强度检算应符合
γ·Δσp≤[σ0]
(2)
式中:[σ0]为疲劳容许应力幅(MPa);γ为桥梁损伤等效系数,取γ=1.4。
在规范1的第5.2.5条中规定:钢桥的疲劳活载应采用运营列车活载,其动力系数应按第5.2.4条规定的动力系数的0.75倍进行取值;钢桁梁的纵梁、正交异性钢桥面板的纵肋,应根据单线荷载可能出现的最不利情况进行加载。
对于城市轨道交通正交异性钢桥面板的疲劳验算,规范1对轨道列车的冲击系数与加载线路(单线荷载)均有明确的规定。
城市轨道交通的其他钢结构的疲劳检算可以参考《铁路桥梁钢结构设计规范》(TB10091—2017)[6],但城市轨道交通的正交异性钢桥面板须遵循规范1的相关内容。基于城市轨道交通的车辆特征,城市轨道交通钢桥面板的疲劳强度验算有其独特性。规范1中的桥梁损伤等效系数γ的取值为1.4,有必要进一步开展研究。
2 损伤等效系数法的基本原理
根据Miner线性累积损伤理论,在ni个循环的变幅应力幅Δσi作用下造成的疲劳损伤为
(3)
根据Miner线性累积损伤理论和S-N曲线,城市轨道交通钢桥面板的总疲劳损伤可由各级应力幅及对应循环次数计算得到。为方便说明,用各级应力幅中的最大值Δσmax和对应总损伤换算得到的循环次数nmax表示结构的总疲劳损伤。当采用单斜率的S-N曲线时,等效应力幅计算式为
(4)
令
(5)
式中:Δσmax为一列轨道交通列车通过钢桥时疲劳细节产生的最大应力幅值;nmax为设计使用年限内造成的疲劳总损伤按最大应力幅换算得到的应力循环次数。由于城市轨道交通在设计年限内的发车次数突破500万次,故m的取值为5。
3 城市轨道交通的交通荷载调研
本文列举4个城市的4条轨道交通线路的列车荷载特性。A市轨道交通1号线列车的每日运营时间为06:00—23:00,早高峰时段为每日07:30—09:30,晚高峰时段为每日16:30—19:30。将单日列车运营时间划分为若干时间段,统计出的客流,结果如表1所示。乘客重量平均按60 kg/人计入。单向客流量为30.1万人/d。由表1可见,A市轨道交通1号线的载客平均轴重与空车平均轴重的比值为1.04~1.27,最大值仅为1.27。

表1 A市轨道交通1号线单日乘客量统计表(单向客流量30.1万人/d)
B市轨道交通2号线列车的每日运营时间为06:30—23:00。根据该线路的发车特点,将其客流分布情况划分为8个时间段,客流量为21.02万人/d。该线路的载客平均轴重与空车平均轴重的比值为1.02~1.21,最大值仅为1.21。
C市轨道交通3号线列车的一部分路段采用6辆编组轻轨车运营,另一部分路段采用6辆轻轨车辆编组和8辆轻轨车辆编组混跑。该线路列车每日运营时间为06:30—22:30,根据该线路的发车特点,将其单日列车的运营时间划分成若干个时间段。该线路的载客平均轴重与空车平均轴重的比值为1.05~1.51。
D市轨道交通6号线的列车每日运行时间为06:00—24:00。根据该线路的行车特点,选择了该线路中具有控制节点意义的某跨江大桥进行交通量调查。该线路某跨江大桥的载客平均轴重与空车平均轴重的比值为1.02~1.15。
4 城市轨道交通正交异性钢桥面板的应力影响线特征
为了研究正交异性钢桥面板在车辆通过时产生的疲劳应力特性,采用有限元软件ANSYS进行数值模拟。将车轮作用力以节点作用力的形式施加在模型端部。分单轮、双轮两种情况进行移动加载,可以得到正交异性钢桥面板关键部位的应力影响线。
4.1 计算模型及关键疲劳验算点
由于正交异性钢桥面板结构复杂,构造细节多,此处只考虑闭口肋正交异性钢桥面板的4个最关键的疲劳细节,如图1所示。
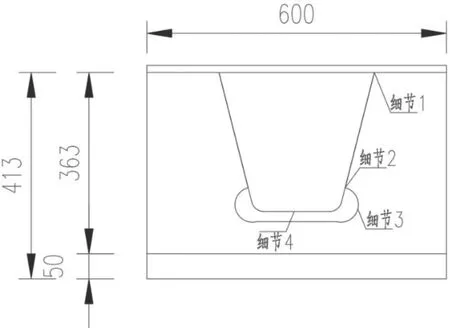
图1 4个关键疲劳细节
模型整体尺寸为10.0 m×9.0 m,顶板厚14 mm,共设置7道U形加劲肋,U形加劲肋厚8 mm,内设3片横隔板,横隔板的间距为2.7 m。用ANSYS软件建立有限元模型(见图2),用弹性板单元SHELL63模拟各板,该板单元的每个节点有6个自由度,即x、y、z方向的平动自由度和绕x、y、z轴的转动自由度。
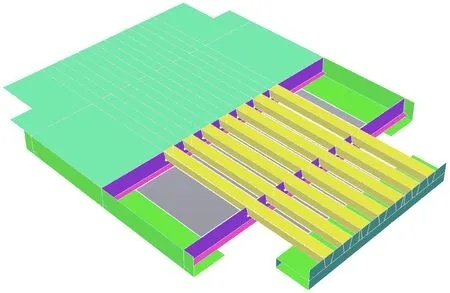
图2 有限元模型
4.2 车辆加载示意图
将车轮对模型的作用以节点荷载的形式施加在节点上,单个车轮作用力设为1 kN。为准确反映关键部位测点的受力情况,将车辆加载分为两种情况:一是将单轮荷载作用于正交异性板上,从模型的左端移动至右端,得到加载过程中关键部位的应力影响线;二是将双轮荷载作用于正交异性钢桥面板上,首先将左轮作用于模型的最左端,然后向右端进行移动加载,直至右轮移动至模型最右端时停止加载,得到该过程中关键部位的应力影响线。双轮加载如图3所示。

图3 双轮作用示意图(单位:m)
4.3 关键细节的应力影响线
在单轮加载及单位荷载(1 kN)作用下,模型的关键部位各测点的应力影响线如图4所示。

(a)细节1

(b)细节2

(c)细节3
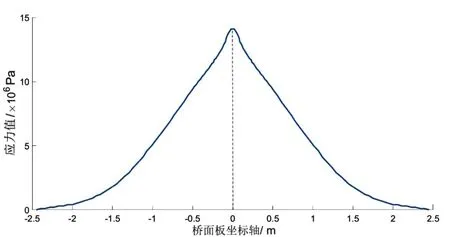
(d)细节4
当节点荷载位于正交异性钢桥面板结构中间时,关键疲劳细节1的疲劳应力达到最大正值8.26 MPa,关键疲劳细节2的疲劳应力达到最大负值-1.5 MPa,关键疲劳细节3的疲劳应力达到最大正值1.1 MPa,关键疲劳细节4的疲劳应力达到最大正值1.41 MPa。各关键疲劳细节的应力峰值多位于中横隔板处,应力峰值均为1个。
在双轮加载情况下(用于模拟列车的转向架的2个轴载),在单位荷载(1 kN)作用下,关键部位各测点的疲劳应力影响线如图5所示。当双车轮加载至正交异性钢桥面板中间关键位置时,关键疲劳细节1达到最大正值9.1 MPa,关键疲劳细节2达到最大负值-2.8 MPa,关键疲劳细节3达到最大正值1.89 MPa,关键疲劳细节4达到最大正值2.58 MPa。各关键疲劳细节的应力峰值大都位于中横隔板处,除了关键疲劳细节1有2个应力峰值外,关键疲劳细节2~4的应力峰值均为1个。

(a)细节1
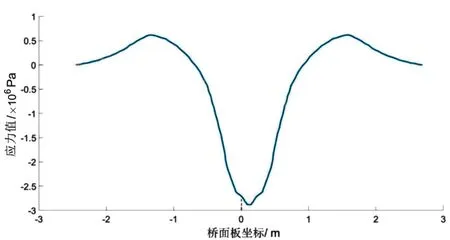
(b)细节2
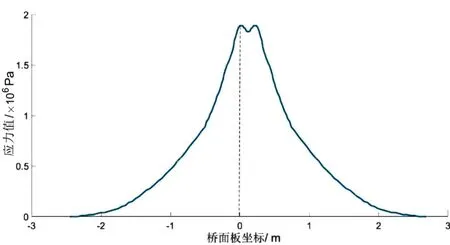
(c)细节3
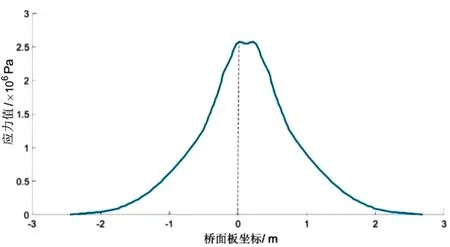
(d)细节4
4.4 应力情况对比
上述模拟结果如表2所示。对于关键疲劳细节1,可以认为1个轴产生1次应力循环。相邻轴的影响增大约10%;对于关键疲劳细节2~4,则是相邻的2个轴累计产生1次应力循环,累加效应约为单轴效应的1.9倍。

表2 单位集中荷载作用下的关键疲劳细节的应力情况对比
列车通过时,在绝大多数情况下,每个轮轴产生1次应力循环。当轮轴间隔较小(如列车的相邻转向架)时,通常2个轴产生1次应力循环。在个别情况下,一辆列车产生1次应力循环。除了有限元模拟外,本文有限元计算模拟及其他研究文献的实桥实测也证实了此点[12-14]。正交异性钢桥面板的某个细节在一辆列车通过时产生的应力循环次数与应力纵向影响线的长度和车辆轴距等有关,情况相对复杂[7-11]。轨道交通桥梁正交异性钢桥面板实桥应力测试试验也证实了该结论[14]。
5 城市轨道交通正交异性钢桥面板的疲劳损伤系数研究
5.1 损伤系数的组成分析
Eurocode规范[15]与《公路钢结构桥梁设计规范》(JTG 64—2015)(简称规范2)[5]定义的损伤等效系数与多种独立因素有关,分别用λ、λ1、λ2、λ3、λ4表示,即
λ=λ1·λ2·λ3·λ4,λ<λmax
(6)
式中:λ1为损伤效应的系数,与影响范围区域或影响线临界长度有关;λ2为考虑年交通量的系数;λ3为考虑桥梁设计使用年限的系数;λ4为当结构承受多于1个轨道荷载作用时的修正系数;λmax为根据疲劳极限得出的最大λ值。
在城市轨道交通正交异性钢桥面板的疲劳细节中,对于损伤等效系数λ1而言,主要体现了疲劳细节的影响线临界长度,而正交异性钢桥面板的影响线长度相对较短,一般不超过2个横隔板的长度。
损伤等效系数λ2与交通量有关。由于城市轨道交通的发车量远远大于200万次,而规范1中规定的正交异性钢桥面板容许应力幅是基于200万次。因此需要重点研究损伤等效系数λ2,即本文研究的基于列车荷载作用频次的城市轨道交通正交异性钢桥面板疲劳损伤系数修正因子。
λ3为考虑桥梁设计使用年限的系数。由于城市轨道交通的重要性,其设计寿命是100 a。λ3可以取值为1。
λ4为当结构承受多于1个轨道荷载作用时的修正系数。由于正交异性钢桥面板的影响线长度相对较短,规范1中第5.2.5-3条明确规定,正交异性钢桥面板的疲劳验算应按单线轨道的最不利轨道列车荷载进行布载。因此本文只研究单个轨道列车荷载布载时的疲劳损伤系数,即λ4=1。
鉴于城市轨道交通正交异性钢桥面板疲劳细节的结构与荷载特点,式(6)疲劳损伤系数的4个系数中,仅有2个与城市轨道交通正交异性钢桥面板疲劳细节相关,即疲劳细节影响线范围与发车次数,因此可以合并为列车荷载作用频次,即式(5)。
5.2 疲劳损伤系数的取值
分析可知,各统计线路的列车载客平均轴重与空车平均轴重的比值范围约为1.02~1.51。由于列车的自重占比很大,每个车辆的轴重均对钢结构的疲劳损伤有影响,因此城市轨道交通正交异性钢桥面板不宜如规范1所规定的低于某个值的轴重不计入其疲劳作用进行处理。对于正交异性钢桥面板的细节1,轨道车辆的1个车轴会对细节1产生1次应力循环。对于正交异性钢桥面板的细节2~4,轨道车辆的相邻的2个轴累计对细节2~4产生1次应力循环。
以交通量较大、有一定代表性的C市三号线的某跨江钢桥的城市轨道交通正交异性钢桥面板为例,研究基于列车荷载作用频次的城市轨道交通正交异性钢桥面板的疲劳损伤系数。
根据交通规划,该桥的初期时限是7 a(2007—2013年),近期时限是15 a(2014—2028年),远期时限是78 a(2029年至未来)。初期每日的发车量是290次,近期每日的发车量是348次,远期每日的发车量是348次。因此,在100 a的设计寿命期内,通过该钢桥的总发车量是12 553 810次。总发车量也超过了500万次,说明m的取值为5是合适的。
由于不同时段的乘客数量(人流量)不同,所以不同时段的载客平均轴重/空车平均轴重的比值不同。城市轨道交通的轴重比例变化相对较小,轴重相对均匀,因此每一列车的每个轴重都对城市轨道交通钢桥结构的疲劳有一定的影响。在100 a的设计寿命周期内,该线路的发车总量约为1 255万次,远远超过了200万次。需要考虑列车荷载作用频次对城市轨道交通钢桥面板疲劳损伤的影响,并进行相应的系数修正。细节1的基于列车荷载作用频次的城市轨道交通正交异性钢桥面板的疲劳损伤系数为2.84,细节2~4基于列车荷载作用频次的城市轨道交通正交异性钢桥面板的疲劳损伤系数为2.48。这与规范2中规定的γmax=2.5比较接近。γmax=2.5对应于影响线长度小于10 m的情况,正交异性钢桥面板的影响线长度一般小于10 m,二者结果一致。
当列车通过时,每节车厢都会依次通过该截面,结合轨道交通车辆运营的实际情况,如果1辆轨道车辆只对某个关键疲劳细节产生1次应力循环,则基于列车荷载作用频次的城市轨道交通正交异性钢桥面板的疲劳损伤系数为1.44。该疲劳损伤系数与规范1中规定的γmax=1.4比较接近。
基于不同列车发车次数提出的3个基于列车荷载作用频次的城市轨道交通桥梁疲劳损伤系数可以根据城市轨道交通正交异性钢桥面板的构造细节与城市轨道交通量特点进行选用。
6 结论
(1)调研结果表明,各线路的载客平均轴重与空车平均轴重的比值不同,比值为1.02~1.51。轨道交通车辆的轴重比例变化相对较小,每一列车的轴重都对钢桥结构的疲劳有一定影响。
(2)相关规范的损伤等效系数的4个系数中,仅有疲劳细节影响线范围与发车次数的2个系数与城市轨道交通正交异性钢桥面板相关。
(3)考虑正交异性钢桥面板的4个关键疲劳细节的应力循环次数,基于使用寿命期内的列车发车数,提出了3个基于列车荷载作用频次的城市轨道交通钢桥面板疲劳损伤系数,即2.84、2.48和1.44。
