改进GM(1,1)-ARIMA-LR模型天然气产量预测研究
2024-03-05林文辉杜彦炜
林文辉,杜彦炜,赵 鹏
(1.西安工业大学 机电工程学院 ,西安 710021;2.西安工业大学 新生院,西安 710021)
能源是现代经济社会发展的基础,过去100年世界能源结构发生了巨大变化,天然气在能源结构中所占比例正稳步上升[1]。相比于即将到来的原油峰值,距中国天然气产量(下文简称天然气产量)达峰仍有数十年[2],结合未来天然气水合物勘探开发的突破,天然气产量增长潜力较大[3]。一方面我国提出2030年碳达峰的目标,另一方面碳达峰不能以损害能源安全为代价[4]。天然气作为化石能源中的清洁能源,在相当长一段时间内将是我国能源战略和碳减排实施的重要保障[5]。而研判能源发展形势,谋划天然气战略布局又对天然气的产量预测提出迫切要求。
天然气产量预测方法主要包括生命旋回模型、储采比控制法、产量构成法等。生命旋回模型中,广义翁氏模型和Hubbert模型最为常见,其将产量的周期性变化视作一个生命旋回,通过构建循环模型进行预测。文献[6]提出一种指数修正翁氏模型用于四川盆地油气预测,文献[7]采用多循环Hubbert模型预测了中国未来天然气产量。储采比即剩余可采储量与当年实际产量的比值,反映了油气资源的保证程度。文献[8]运用油藏数值模拟等方法,得到储采比与累计产量、采出程度等之间的关系。产量构成法依据不同类型的气藏在不同阶段的生产规律、剩余可采储量等指标,计算每个单位的产量潜力,按照时间累加得到总产量的规模。文献[9]使用产量构成法预测分别预测未来中国常规天然气产量、非常规天然气产量以及溶解气产量。
近年来国内外学者开始将自回归滑动平均求和模型(Autoregressive Integrated Moving Average Model,ARIMA)等计量经济学模型及机器学习方法用于天然气产量预测。文献[10]将自回归滑动平均求和模型与长短期记忆神经网络(Long Short-Term Memory,LSTM)结合起来建立天然气产量的集成预测模型,文献[11]提出一种季节性灰色模型用于对天然气产量进行预测,使用粒子群算法优化模型参数,文献[12]基于多目标随机森林模型对页岩气产量进行预测,文献[13]基于Logistic模型,将原模型中的“环境容量”和“种群内禀增长率”两个常量参数函数化以改进模型,使用改进Logistic模型对中国天然气产量进行了预测。
以往研究未充分考虑天然气产量序列的时序趋势、不同预测步长下的模型变化以及对过去预测误差信息的利用。基于此,本文先选取能够较好捕捉中短期时序特征的ARIMA模型,对序列异常波动具有强抗扰动能力、长期预测效果稳定的线性回归(Liner Regression, LR)模型,和针对信息不完全的情形有较好表现的GM(1,1)模型进行组合,以进行模型之间的互补。再加入自适应学习因子与组合学习因子,分别对单个模型和组合模型加以改进,实现对过去预测误差信息的充分利用,使得最终的集成预测模型具有更高的预测精度。
1 相关方法
1.1 ARIMA模型
ARIMA模型是由Box和Jenkins提出的一类时间序列分析方法[14],其通过差分对序列平稳化,可用于非平稳时间序列的预测,在模型建立充分使用观测到时间序列的过去项、当前项和误差扰动项,从而使模型具有较高的预测精度。
用{Yt}表示观测到的时间序列,εt表示未观测到的白噪声序列,即一组服从独立同分布、均值为零的随机变量。φ表示白噪声变量的权重,则{Yt}可表示为一系列白噪声变量的加权线性组合[15]:
Yt=εt+φ1et-1+φ2et-2,
(1)
当φ不为零时,用1,-θ1,-θ2,-θ3,…,-θq作为et,et-1,et-2,…,et-q的权重加平均得到{Yt},即得到q阶滑动平均过程(MA),记为MA(q):
Yt=et-θ1et-1-θ2et-2-…-θqet-1,
(2)
当用{Yt}自身做回归变量时,用ψ1,ψ2,ψ3,…,ψp作为Yt-1,Yt-2,…,Yt-p的权重,{Yt}对应的白噪声变量et表示无法用自身解释的新信息项,得到p阶滑动平均过程,记为AR(p):
Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+et,
(3)
若序列中部分是自回归,部分是滑动平均,可得到一个混合过程,即自回归滑动平均过程,记为ARMA(p,q):
Yt=et-θ1et-1-θ2et-2-…-θqet-q+φ1Yt-1+
φ2Yt-2+…+φpYt-p+et,
(4)
ARMA要求时间序列具有平稳性,在序列非平稳的情形下,需通过差分计算使序列平稳化,表示向后差分算子,Yt表示Yt的一阶差分,即:
dYt=θ0+θq(B)εt,
(5)
如果{Yt}的d次差分Wt服从ARMA(p,q)模型,则称{Yt}为ARIMA(p,d,q)过程。参数p,d,q用来分析时间序列,即描述自回归阶数p、差分次数d和移动平均阶数q,表示为[15]:
dYt=θ0+θq(B)εt,
(6)
式中:θq为移动平均算子;θ0为常数项;B为后移算子,BYt=Yt-1,定义θ0=u(1-φ1-φ2-…-φp),其中u为平均数。
由于传统的通过观察模型自相关函数的差分数据图(auto correlation function,ACF)和偏自相关函数的偏自相关图(patial auto correlation function,PACF)进行估计模型参数的方法在多次预测时耗时长、带有一定的主观性,本文使用统计学中的贝叶斯信息准则(Bayesian Information Criterion,BIC)指标,通过对指定参数范围内的模型进行比较,实现对模型的自动定阶。
1.2 灰色GM(1,1)
灰色指的是信息不完全,由于天然气产量变化与许多因素有关,而仅使用历史天然气产量数据构建的一个预测系统可视为一个信息不完全的系统,即灰色系统。灰色GM(1,1)是通过对原始数据进行累加生成来进行建模,再对预测结果进行累减还原得到预测结果[16],其适用于对小样本、贫信息的不确定系统进行预测[17]。
设原始序列Y(0)=(y(0)(1),y(0)(2),…,y(0)(n)),其中y(0)(t)≥0,t=1,2,…,n;Y(1)为Y(0)的一阶累加序列:
Y(1)=(y(1)(1),y(1)(2),…,y(1)(n),
(7)

y(0)(t)+ax(1)(t)=y,
(8)
为GM(1,1)模型[17]。式中,a称为发展灰数,反映Y(1)及Y(0)的发展趋势,u称为内生控制灰数,体现数据间的变化关系。利用最小二乘法求解得到a、u,继续求解微分方程式
(9)
作累减还原后,便可得到预测值
(10)
1.3 LR模型
回归是通过一定的数学表达是将变量之间的关系描述出来的一种方法,当所要描述的因变量y和自变量x之间为线性关系时,则称为线性回归(Liner Regression,LR)。自变量个数为1时,称为一元线性回归。以下是一元线性回归模型的表示,ε表示误差项[18]:
y=β0+β1x+ε,
(11)
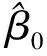
(12)
高斯提出用最小化离差平方和来估计参数β0和β1,这一估计方法称为最小二乘法,根据最小二乘法,令
(13)
解上式得
(14)
2 GM(1,1)-ARIMA-LR模型的构建
2.1 自适应学习因子
单个模型在进行预测的时候,可能由于时滞以及模型本身特性的影响,导致预测结果总是偏大或偏小。此时尽管模型的预测误差平均值较大,但预测误差的方差较小,即预测结果较为稳定。若是直接将这样的几个模型进行集成,由于单个模型的预测误差较大,集成模型的效果将受到影响。文中提出一种自适应学习因子F1,如式(15)所示。先通过模型对历史数据进行预测后得到一个预测误差百分比列表E,然后将当前时间减去预测步长得到上个周期对应时间t-k。
将上个周期的预测误差百分比进行变换后与模型本身相乘,从而得到修正后的预测结果。
(15)
2.2 组合学习因子
通过加权平均对模型进行集成,关键在于模型的选取以及权重系数的确定。权重系数大多采用两种方式确定,一是平均策略,对每个模型赋予一样的权重,二是通过不断尝试选取较佳的权重。但这样的做法以下问题:一是难以取到最优权重,二是权重的选取具有较强的主观和偶然性,三是权重选取的方式是静态的,难以适应预测步长的变化。在一步预测误差较小的权重系数,可能预测步长改变时误差放大。为提升集成模型预测精度,本文根据预测步长的不同设置可变的权重系数,并且建立一个目标规划模型,将求解得到的权重系数命名为组合学习因子F2。
本文通过改变参与预测的数据集来实现预测步长对权重系数的调节。若对天然气产量进行单步预测,则选取起始年份至预测年份前一年的数据。若对天然气产量进行多步预测,则先用预测年份减去预测步数得到一个终止年份,再选取起始年份到终止年份的数据作为数据集。例如,要进行一步预测得到2023年天然气产量的预测值,则选取2002~2022年数据作为输入数据集。要进行二步预测得到2023年天然气产量的预测值,则选取2002~2021年数据作为输入数据集。
目标规划模型以近5年天然气产量预测平均误差百分比的绝对值最小为目标为
(16)
式中:Ri为天然气产量数据的实际值;Pi为集成模型的预测值。
由于目标函数中带有绝对值,为便于模型求解,引入辅助变量Q,加上第二、三约束条件,可去掉目标函数中的绝对值,进而目标函数可表示为
(17)
为了更清晰地表示,可将上式等价为
(18)
式中:y为时间片段的长度,即取y年平均误差百分比作为目标值。y取1、2时容易受异常值的影响,所以分别将y取3、4或5,最后取对应目标值最小的解作为最优解。所以目标函数可进一步表示为
(19)
接下来是约束部分。权重系数优化模型的第一个约束,是Pt的求解:
(20)
式中:a为ARIMA模型的权重系数;b为灰色GM(1,1)的权重系数;c为LR模型的权重系数;A为ARIMA模型的预测值;G为灰色GM(1,1)模型的预测值;L为LR模型的预测值。
第二、 三个约束,是引入辅助变量Q后新增的约束:
(Ri-Pi)/Ri≤Qj,
(21)
(Ri-Pi)/Ri≤Qj,
(22)
第四个约束即权重系数的非负约束为
a,b,c>0,
(23)
综上所述,权重系数的优化模型表示为
(24)
组合学习因子即上述权重系数优化模型求解得到的系数a、b、c,应用组合学习因子对所要预测年份的各单模型预测值进行加权求和,即可得到集成模型的预测值Pt:
F2=[a,b,c]
Pt=[a,b,c]×[At,Gt,Lt]T,
(25)
2.3 GM(1,1)-ARIMA-LR集成预测模型
GM(1,1)-ARIMA-LR集成模型预测框架如图1所示。首先获取数据集,根据步长选取数据,分别使用ARIMA、GM(1,1)、LR模型进行预测得到初步结果,再加入自适应学习因子F1对结果进行调整得到改进后的结果。将得到的单个模型预测结果输入已建立的权重系数优化模型,求解后得到组合学习因子F2。最后对模型进行融合,输出GM(1,1)-ARIMA-LR模型预测结果。

图1 GM(1,1)-ARIMA-LR预测框架
3 实例预测结果与分析
3.1 数据获取及处理
从国家统计局网站获取1973-2022年中国天然气产量(亿立方米)年度数据。首先进行ARIMA、灰色GM(1,1)和LR单模型的预测。天然气产量数据的趋势图如图2所示,整体上天然气产量变化呈稳定上升趋势,曲线斜率接近。但是在一些年份,如1980年、1993年、2009年、2017年等,天然气产量的曲线斜率发生了较大的变化。
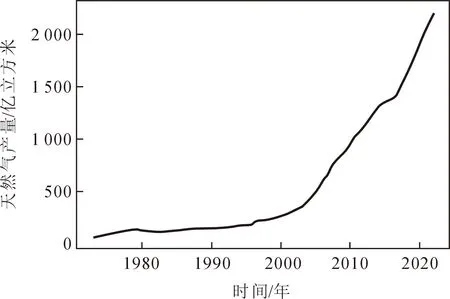
图2 1973~2022年天然气产量
预测算法程序采用Anaconda3开发,软件环境为Python3.9.7,硬件运行环境为Windows10、64位操作系统,处理器为Intel(R)Core(TM)i5-7300HQCPU@2.50 GHz,内存8 GB。
3.2 预测建模
将数据集分别代入ARIMA、GM(1,1)、LR模型进行预测,接着根据自适应学习因子F1对模型进行调整。图3为一步至八步预测的ARIMA模型与改进ARIMA模型预测误差的比较,观察图3可见,在一到四步预测,使用自适应学习因子对模型进行改进显著降低了模型预测误差,而在五到八步预测,该改进反而使预测误差增大。因而在集成模型的构建中,加入变量SA,决定是否加入自适应学习因子F1。

图3 ARIMA模型改进前后误差对比
当预测步长k≤4时,取SA=1,表示加入F1,对ARIMA模型进行改进,并用改进ARIMA模型进行预测;当预测步长k>4时,取SA=0,表示不加入F1,直接使用原ARIMA模型得到预测结果。
同理,观察图4和图5可见,当预测步长为一到四时,改进后的GM(1,1)预测误差大幅降低,预测步长为五到八时,改进后GM(1,1)预测误差反而增大。在一到八步预测,改进后LR模型预测误差均显著降低,因而可一直应用F1对LR模型进行改进,加入变量SG,决定是否加入自适应学习因子F1对GM(1,1)模型进行改进。

图4 GM(1,1)模型改进前后误差对比
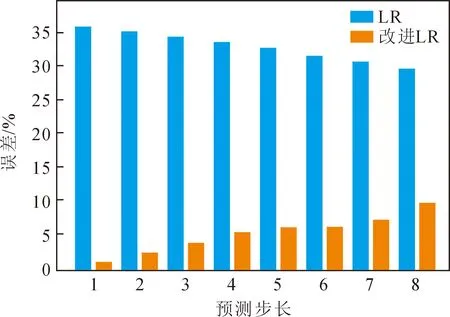
图5 LR模型改进前后误差对比
当预测步长k≤4时,取SG=1,表示加入F1,对GM(1,1)模型进行改进,并用改进GM(1,1)模型进行预测;当预测步长k>4时,取SG=0,表示不加入F1,直接使用原GM(1,1)模型得到预测结果。
继续将上述得到的初步预测结果代入权重系数优化模型,求解得到对应的权重系数,即组合学习因子F2。通过对比发现,在一、二步预测中,改进GM(1,1)模型预测误差最小,分别为1.187%,2.695%;在三到五步预测中,改进GM(1,1)-ARIMA-LR模型表现较优,预测误差分别为4.243%,2.698%,3.129%;在六到八步预测中,改进LR模型效果较好,预测误差分别为6.550%,7.423%,9.880%。
通过设置权重系数的方式,可令一到二步的短期预测中系数a,b,c的值为0,1,0,六到八步的长期预测中,系数a,b,c的值为0,0,1,三到五步a,b,c的值则继续使用权重系数优化模型得到的结果,从而进一步调整得到最终的改进ARIMA-GM(1,1)-LR模型。以2022年为例,权重系数的变化如图6所示。

图6 权重系数变化
可见,随着预测步长的增加,GM(1,1)模型的权重占比越来越小,LR模型的权重占比越来越大。说明在进行不同步长的预测过程中,ARIMA,GM(1,1)、LR模型实现了互相补充,从而使得改进ARIMA-GM(1,1)-LR模型具有更高的预测精度。
3.3 预测效果评价及对比分析
以一步预测为例,表1为一步预测的结果对比,可展示为如图7所示。观察图7可见,在一步预测中,改进GM(1,1)的预测误差最小,因而选择改进GM(1,1)模型进行一步预测。

表1 一步预测结果对比

图7 一步预测结果对比
图8为多步预测的模型误差对比。可以发现,随着预测步长的增长,模型的预测误差也在不断增加。集成模型ARIMA-GM(1,1)-LR的预测效果最好,改进LR模型预测误差较为稳定,随预测步长增加变化小。改进GM(1,1)模型在一到二步的短期预测中表现优异,之后预测误差骤增。
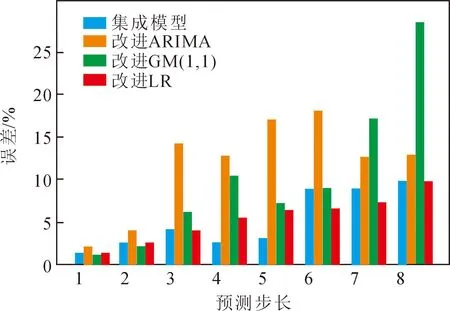
图8 各步长下预测误差对比
3.4 2023-2030年天然气产量预测
根据求解得到的自适应学习因子F1和组合学习因子F2,对ARIMA、GM(1,1)、LR进行加权求和,得到2023-2030年中国天然气产量预测结果,见表2。2023年的天然气产量为2022年天然气产量的一步预测值,2024年的天然气产量为2023年天然气产量的二步预测值,以此类推。

表2 2023-2030年天然气产量预测结果
4 结 论
1) 文中从对预测误差信息的利用角度出发,设计了自适应学习因子和组合学习因子,对ARIMA、GM(1,1)、LR模型进行改进,使得集成后的模型误差大幅降低,在天然气产量的短期、中期与长期预测均具有优异表现。
2) 文中主要聚焦于小样本情形下提高天然气产量的预测精度。在样本容量大、数据维度高的情形下,将影响天然气产量变化的众多因素考虑在内,应用深度学习等方法构建多变量预测模型或能增加预测精度,这是本研究之后改进的方向。
