基于线结构光扫描的工件高精度三维测量方法

洪汉玉，吴裕强，叶 亮，邵 洋

武汉工程大学电气信息学院，湖北 武汉 430205

现代工业的快速发展对工件的高精度设计、制造和质量评价提出了日益严格的要求［1］。在生产和制造过程中，需要对工件的三维形状和尺寸进行准确的测量和分析，以确保产品的质量和性能。目前，三维测量技术包括接触式和非接触式2种方法。接触式测量方法［2］通过高精度测头逐点获取被测曲面的三维数据，测量效率低且人工成本高。由于直接接触被测工件，该方法容易损坏接触面，限制了其在现代工业自动化检测中的应用。非接触式测量方法主要包括飞行时间法［3］、立体视觉测量法［4］、全息干涉法［5］、超声测量法［6］和结构光测量法［7-8］。这些方法各自具有独特的优势和限制。例如，飞行时间法原理简单且可靠，但精度取决于信号处理系统的时间分辨率，且测量效率较低。全息干涉法测量精度较高，但应用场景相对较窄，且容易受到光学散斑和振动等环境变化的影响。立体视觉测量法测量范围广，但处理过程复杂，计算量大，无法兼顾速度和精度。超声测量法通过路径规划可以实现自动测量，但精度相对较低。结构光测量法根据投射图案的形态可以分为点结构光、线结构光和面结构光。基于线结构光扫描的三维测量方法具备结构简单、测量精度高、速度快、稳定性高等特点，被广泛应用于航空航天、汽车、能源、医疗和建筑等领域。

本文设计并实现了一种基于线结构光扫描的高精度非接触式三维测量系统。采用双远心镜头［9］以恒定的放大倍数成像，确保成像大小与物体实际尺寸呈固定比例，以提高图像采集的精度。在数据采集过程中，影响测量精度的关键因素之一是提取每帧图像中的线结构光中心线。灰度质心法［10］是一种常用提取算法，但该方法容易受光源均匀性的影响，而且需要大量的计算。因此，本文改进了灰度质心法，提出了一种基于差分区间的灰度质心法，该算法提高了提取精度并降低了计算量。根据每帧图像提取的线结构光中心线的偏移计算被测工件表面各点的高度，然后将数据整合，生成工件的表面点云数据，这些原始点云数据通常包含噪声点和冗余点，为了提高测量的精度，需要进行点云滤波和精简处理。为了进行误差分析与评定，将经过预处理的点云与计算机辅助诊断（computer aided diagnosis，CAD）模型进行精确配准对齐，然后利用配准后的数据进行轮廓度误差计算。

1 原理及方法

1.1 点云数据采集

本文设计的三维测量系统的实物图如图1 所示，主要由计算机、视觉系统和高精度运动控制系统组成。

图1 设计的三维测量系统Fig.1 Design of three-dimensional measurement system

视觉系统主要包括相机、双远心镜头、左/右线结构光发生器，其中，相机的分辨率为2 448×2 048，像素尺寸为3.45 μm×3.45 μm；双远心镜头视场尺寸为10.5 mm×8.8 mm，工作距离为126~178 mm；光纤耦合线结构光发生器波长为650 nm，扇形角为20°。各部件通过金属支架固定，安装好后相对位置不变。置物平台水平安装，相机与镜头的工作方向垂直于置物平台所在的平面，线结构光发生器入射方向与置物平台呈一定夹角。运动控制系统由3 套电机、控制器组成，形成空间上3 个方向的运动轴，使置物平台和被测物体能够在Y轴方向上移动，视觉系统能够在X轴和Z轴方向上移动，从而构成一个3 自由度的测量平台。

1.1.1 数据采集流程 系统的数据采集流程如图2所示，首先，线结构光发生器投射光线到被测物体表面，分别与被测物体和置物平台相交，形成线结构光。然后，相机捕获线结构光图像，经过图像预处理后进行中心提取，得到单像素的线结构光中心线图像。接下来，通过三角测量法并结合标定得到转换系数，求解相应的三维坐标，将其转换为单帧的三维点云数据。最后，通过运动控制系统使被测物体与视觉系统发生相对位移，进行扫描以形成图像序列，重复上述过程，得到被测工件的原始点云数据。

图2 数据采集流程示意图Fig.2 Schematic diagram of data acquisition process

1.1.2 线结构光中心提取 数据采集中，线结构光中心的精确提取至关重要，直接决定了测量的精度。本文提出了一种基于差分区间的灰度质心法，该算法利用多阶后向差分公式［式（1）］，计算线结构光条纹中心的提取差分区间。

其中，l为差分模板长度，d(x,y)和g(x,y)分别表示当前像素点（x，y）的差分值和灰度值，其中x为列坐标，y为行坐标。

基于差分区间的灰度质心法的原理示意图如图3 所示，其中，实曲线和虚曲线分别表示线结构光图像的第i行的差分值和灰度值曲线，X方向上的差分区间[xmin,xmax]由差分的最大值Smax和最小值Smin确定：

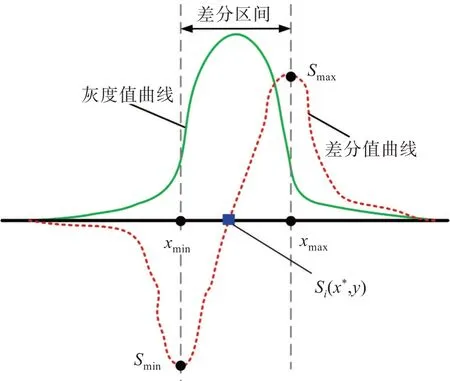
图3 基于差分区间的灰度质心法原理示意图Fig.3 Schematic diagram of grayscale centroid method based on differential intervals

则第i行的线结构光中心点Si(x*,y)应在差分区间[xmin,xmax]内，其中y=i且X方向上的坐标x*∈[xi_min,xi_max]，x*由二次加权的灰度质心法确定：

根据提取方向，逐行计算出中心点，生成单像素的线结构光中心线图像。基于差分区间的灰度质心法运用多阶后向差分公式，计算出线结构光所在列的像素范围，从而避免对整行像素进行计算，大幅度降低了计算量。此外，引入二次加权的灰度质心法来确定线结构光的中心点，减小由于图像灰度变化不均匀而导致的误差，提高测量的精度。

1.2 点云处理

由于设备振动、工件表面材质、工作环境、中心线提取误差等因素，采集的工件点云数据不可避免地包含噪声点和冗余点［11］。为了提高三维测量的效率和精度，需要对点云进行预处理。

1.2.1 点云滤波 本文采用一种基于空间分布的点云组合滤波平滑方法，针对原始点云数据的特点，将噪声点分为3 类，然后逐步使用不同的滤波方法进行去除。

（1）采用直通滤波方法去除明显与对象分离且大量聚集的噪声点。该方法基于距离值原理，通过设定一个范围阈值，删除在该阈值范围内的点云数据。

（2）采用高斯统计滤波［12］方法滤除远离对象离群点。该方法基于点云数据的邻域统计信息来判断点云是否为噪声点，利用如式（4）所示的高斯统计函数Igf来计算点云数据在邻域中的距离分布情况，去除距离分布明显不符合正态分布的点云数据，从而达到去除噪声点的目的。

式（4）中：Wx，y为中心像素(x,y)的邻域；ωd(i,j)为像素(i,j)的空间距离相似度权重因子；I(i,j)为灰度图像位置。

（3）采用滑动最小二乘法［13］对近邻对象的噪声点进行平滑处理。利用移动最小二乘法将点云进行映射处理，通过拟合邻域点实现点云平滑。

1.2.2 点云精简 栅格采样法［14］适用于分布均匀的点云数据，能够较好地保持点云模型的形状特征，同时去除冗余点，具有实现简单和高效的特点。该算法的原理是通过指定栅格大小，将待采样点云栅格化，对于分布在同一栅格中的点云数据，只保留距离栅格中心最近的点，删除其余点，从而得到精简后的点云模型，其原理示意图如图4所示。

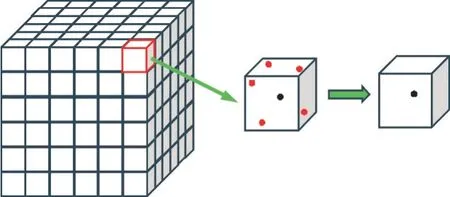
图4 栅格采样法原理示意图Fig.4 Schematic diagram of principle of grid sampling method

1.2.3 点云配准 确立标称形状和实际形状之间的精确映射关系对轮廓精度控制至关重要，通过比较点云和CAD 模型，可以建立此映射，以便进行工件的质量评估。预处理后的点云数据需要与CAD 模型进行配准对齐，才能进行轮廓对比检测分析。实现配准的主要步骤如下：

（1）位置初始化，点云数据的坐标来自系统的测量坐标系，而CAD 模型的坐标是在制图时由设计坐标系确定的。因此，将它们统一到1 个坐标系下时，位置可能存在较大差距。

（2）利用主成分分析法［15］进行粗配准，通过计算点云协方差矩阵的特征值和特征向量，确定点云的主方向，然后计算出对应的旋转和平移矩阵，以实现点云的粗配准，为精配准提供较好的初始位置。

（3）利用迭代最近点（iterative closest point，ICP）算法进行精配准。其原理如图5 所示，点pi为源点云中的点，qi为pi在目标点云中对应的匹配点，Ti表示点qi所在切平面，ni是切平面Ti的法向量，点a表示点pi+在Ti上的投影点。pi+是对点pi应用刚体变换参数g( )R,t进行旋转平移后的点，ICP点到点误差度量迭代匹配的目标函数如式（5）所示：

图5 ICP 配准算法原理图Fig.5 Schematic diagram of ICP registration algorithm

式中，R表示旋转矩阵，t表示平移矩阵，m表示源点云中点的个数。通过最小化距离平方和对目标函数进行求解，以获取最佳刚性变换矩阵参数，从而完成精确的配准操作。

1.3 轮廓误差的测量与评定

轮廓误差评估通常基于实际测量点与理想点之间的差值［16］。将CAD 模型轮廓上的点视为理想点，点云轮廓上的点作为测量点，从而进行误差评定。如图6 所示，CAD 模型轮廓和点云模型轮廓间的差值表示轮廓误差。配准后，假设CAD 模型轮廓上任意一点坐标为Pt(xt,yt,zt)，Pt对应点云轮廓上的点为Pm(xm,ym,zm)，根据式（6）计算点云的轮廓误差di，则轮廓误差的均方根误差σ如式（7）所示。

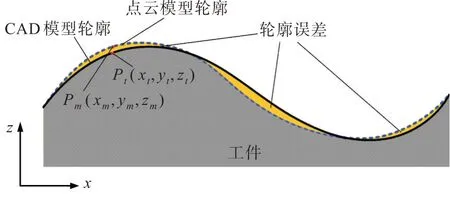
图6 工件轮廓误差示意图Fig.6 Schematic diagram of workpiece profile errors

其中，n为测量次数，di为一组轮廓误差值。

2 结果与讨论

本文采用的测量对象的实物图和CAD 模型如图7 所示。

图7 被测工件：（a）实物图，（b）CAD 模型Fig.7 Measured workpiece：（a）actual object，（b）CAD model

首先，对该工件进行数据采集，获取的原始点云如图8（a）所示。然后进行点云滤波和精简处理，其结果如图8（b）所示。再将处理后的点云数据与CAD 模型进行配准，其配准结果如图9 所示。

图8 工件点云模型：（a）原始点云，（b）预处理完成点云Fig.8 Workpiece point cloud model：（a）raw point cloud，（b）preprocessed point cloud

图9 点云与CAD 模型配准结果：（a）配准前，（b）配准后Fig.9 Registration results of point cloud and CAD model：（a）before registration，（b）after registration

对配准后的点云和CAD 模型在相同位置提取表面轮廓数据，提取位置如图10（a）直线标示，提取结果如图10（b）所示。在模型的X方向上选取10 个测点，各测点位置如图10（b）中①-⑩标示，其在世界坐标系的X坐标值、实际高度值、测量高度值、高度绝对误差以及高度相对误差计算结果如表1 所示。结果显示，对于该工件外轮廓测量的绝对误差小于0.07 mm，相对误差小于0.5%。

表1 工件轮廓高度测量结果及误差Tab.1 Workpiece contour height measurement results and errors

图10 工件表面轮廓线提取位置（a）与提取结果（b）Fig.10 The extracted location（a）and extracted results（b）of the surface contour lines of the workpiece

3 结 论

为满足现代工业对高精度三维测量的需求，本文设计并实现了基于线结构光的高精度非接触式测量系统。通过深入研究线结构光生成点云的原理和相关算法，提出了一种基于差分区间的灰度质心算法，显著提高了线结构光中心线的提取精度和效率。在点云数据处理中，首先采用基于空间分布的点云滤波和栅格采样法进行预处理。然后，通过ICP 算法实现了点云与CAD 模型的精确配准。随后，根据配准后的数据进行工件表面轮廓测量与误差评定。相对于传统的接触式测量中需要人工熟练掌握测量设备、柔性表面接触中易形变或受损、人工操作不精细易导致误差较大等不足之处，本文实现的非接触三维测量系统能够高效、便捷地完成对工件表面轮廓的三维建模并进行精准测量。在实验中，系统对工件外轮廓测量的绝对误差小于0.07 mm，相对误差小于0.5%，具备了足够的测量精度，且建模过程中不需要人工介入，为现代工业领域的高精度三维测量提供了有力的支持。