义务教育不同版本数学教材主题分布比较:基于主题追踪图的研究
2024-03-05杨建强王烨晖郏超超谭玉婷
杨 涛,杨建强,王烨晖,郏超超,谭玉婷
义务教育不同版本数学教材主题分布比较:基于主题追踪图的研究
杨 涛,杨建强,王烨晖,郏超超,谭玉婷
(北京师范大学 中国基础教育质量监测协同创新中心,北京 100875)
教材是课程与教学的重要组成部分.研究基于TIMSS主题追踪图方法,选取中国义务教育阶段4种不同版本数学教材进行分析,并与TIMSS高成就国家和地区的主题分布比较.结果表明:(1)中国4种不同版本数学教材的主题数量随年级变化的整体趋势一致,主题内容都体现出从基础性到高阶性的渐进过程,主题分布有间断的比例在30.3%~48.5%之间,跨3个年级及以上的主题占比在39.4%~57.6%之间;(2)与TIMSS高成国家和地区相比,中国数学教材的主题略多,4年级前各年级的主题数量更多,主题分布的连贯性明显不及TIMSS高成就国家和地区,且年级跨度更小.研究启示:编写教材时要优化主题内容选择,关注教材内容组织方式,重视教材设计,此外要重视教材研究.
数学教材;主题追踪图;主题分布
1 问题提出
教材是课程的重要组成部分,在课程实施中起着重要作用[1].在国际数学和科学趋势研究(Trends in International Mathematics and Science Study,简称TIMSS)课程测量模型中,教材即可能实施的课程,是根据预期课程开发,对实施课程起到直接作用的重要环节[2].教材的研究与建设是课程与教学研究中的核心问题之一,也是教学质量提升、教学改革实施的基本保障[3].
在以往教材研究中,研究者把教育学和心理学作为教科书研究的理论起点和基础视域,探讨教材内容的选择和设计、教材知识的传授,揭示教材的基本特征和理论,其方法包括理论思辨和实证研究[4].教材内容具有价值负载性和思想渗透性,通过教材可以传达主流价值、涵养思想品德,形塑预期的人生观、世界观、价值观,而针对教材的理论思辨,可以对教材的价值观念等进行探讨[5-6].相比而言,基于对经验事实的推理进行的教材实证研究应用更加普遍.在实证研究中,又根据研究方法的差异分为质性研究和量化研究.对数学教材研究方法的梳理后发现,由于教材研究多为文本研究,对教材的文本研究更倾向于描述和归纳,因此文本分析等质性方法应用更多[7].但是定性研究也存在客观性和科学性受到限制的问题,影响研究的科学和推广价值,因此,结合量化研究的教材研究方法逐渐得到研究者的关注和重视[8].
结合量化分析的教材研究发展较晚,在研究范式和研究方法上较少,因此探索结合量化方法对研究教材的必要性更加凸显[9].TIMSS开发的教材评价工具——主题追踪图可以在文本分析的基础上以量化的方式来研究教材的内容数量和分布情况[10].主题追踪图作为可以研究教材主题选择与组织特点的工具,得到了研究者的关注.基于主题追踪图的实证研究,可以比较不同国家和地区的教材编排差异[11],进而探索不同教材对学生的学习机会影响[12]及指导国家和地区的课程改革[13].这些研究的涌现证实了主题追踪图这一方法的有效性,也为教材研究开启了新的范式和方法.
中国的教材研究,尤其是数学教材研究,基于教材的文本分析而开展的教材内容经验总结和讨论相对较多[14].这样的研究方法已经具有较长的历史,也推动了课程的发展和改革,但在研究的科学性和推广性上还有改进的空间[15].因此,有研究者在分析主题追踪图这一方法的基础上,将其引入到国内,对《义务教育数学课程标准(2011年版)》(以下简称《课标》)进行比较分析,从而发现中国小学阶段的《课标》和国外在主题内容和组织上的差异,证实了这一方法在国内课程结构中应用的有效性[16-17].
在中国的课程结构中,教材是反映教学目的和指导教师课程实施的重要材料之一.依据《课标》,目前已有不同教育特色的多版本教材,各地在教材上也有非常大的选择空间和一定的教材选择差异[18].不同版本教材虽然都基于《课标》编制,但又随着不同教材风格和编制者的理解而存在差异,这种差异为整个课程体系带来一定的不确定性,势必会对不同教材的使用者带来不同影响[19].考虑到中国教材的这一特点,结合不同版本教材的使用情况,研究拟选择具有代表性的不同版本数学教材,基于主题追踪图对其进行分析比较.
同时,在教材研究中,比较研究的应用较为普遍,且是教材发展的重要参考来源[20],加强对不同国家和地区教材的研究和比较已成为研究者的共识[21].通过比较分析的方法可以明确现行教材的优势和不足,进而服务于针对性的教材编制和改革.因此,在对国内不同版本教材进行研究的同时,将部分国外高成就国家和地区的教材纳入其中,和中国的不同版本教材进行基于主题追踪图的比较分析.在比较国家和地区的选择上,鉴于TIMSS项目对其参与国的课程的系统分析,选定TIMSS高成就国家和地区的主题分布作为国际比较对象,以明确中国不同版本教材和国际高成就国家和地区的主题内容及分布异同.
综上,基于主题追踪图的方法,分析以下问题:(1)中国义务教育阶段不同版本数学教材,在主题内容和分布上存在哪些主要异同?(2)与TIMSS高成就国家和地区的主题分布相比较,在主题内容和分布上存在哪些主要异同?
2 研究设计
2.1 研究对象
2.1.1 义务教育不同版本数学教材
根据《课标》,国内存在多种版本的教材,各地在教材上也有了非常大的选择空间和一定的教材选择差异.研究拟选取义务教育阶段4个不同版本的数学教材进行分析,主要考虑以下因素:(1)教育部审核通过的数学教材(《课标》发布后编写);(2)全国范围内使用学生人数较多的数学教材;(3)能体现地区特色和课程改革,具有一定代表性的数学教材;(4)研究工作的时间周期的局限.
2.1.2 TIMSS高成就国家和地区主题追踪图
TIMSS项目选定各个参与国家和地区的国家数学课程标准、区域数学课程标准、官方数学教材或使用量最大的非官方教材(当地无官方数学教材时)作为分析对象,确保其覆盖所在国家或地区一半以上的目标学生,通过文本分析、教材图示化等方法对资料进行分析、编码,并制作相应国家或地区的主题追踪图[22].同时,依据学生在数学学业上的表现,TIMSS把参与国家和地区划分为不同的等级,其中最高等级的国家为“A+”国家和地区,包括新加坡、韩国、日本、比利时、捷克共和国和中国香港.由其中大多数(三分之二及以上)“A+”国家和地区确定的主题追踪图常作为国际课程分析比较的基准[23].研究将其作为比较的参考依据,简称为TIMSS A+主题追踪图(如图1最右侧).
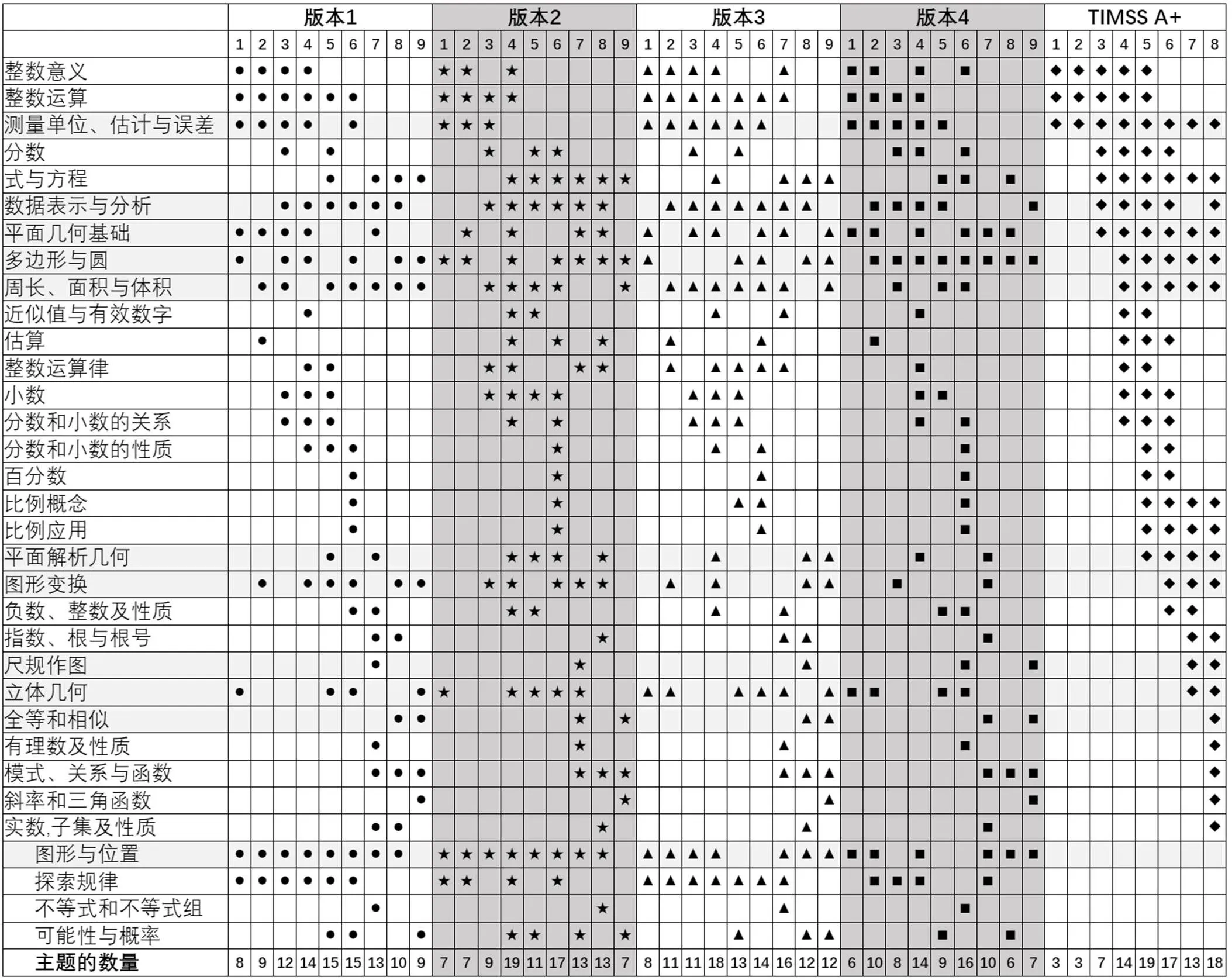
图1 不同版本数学教材和TIMSS A+的主题追踪图
2.2 研究方法
研究对不同教材的测量和分析采用了主题追踪图的方法.主题追踪图是最早被用作在国际比较研究中比较不同国家对同一个知识内容在年级间的具体安排策略的方法[2].具体来看,主题追踪图是根据一定的标准,对所研究的材料经初步分析,明确重点内容及其单元,再对所有材料逐一经过详细的分析、编码和记录等步骤,最后,对结果进行质性和量化结合的分析和比较方法[2].研究基于主题追踪图方法,通过主题追踪图将义务教育阶段不同版本数学教材的主题、数量及其分布特点等内容结构和安排策略,全面、系统、直观地展示出来,对中国不同版本数学教材主题分析,并实现国际比较.主要划分为以下几个阶段.
(1)主题框架的建立、预分析和修订阶段.主题框架是课程测量的主要依据和重要内容之一.框架的建立主要根据教育部制定的《课标》对“课程内容”中一~九年级各个学段的阐述,逐条进行分析、编码、记录,并且与TIMSS国际测评中数学课程分析的主题框架进行比较[23].经过反复的研讨、修改,初步确立适合中国数学课程测量的主题框架.
预分析的目的在于检验主题框架的适切性.对发现的问题、不确定性、遗漏等内容和条目,反复进行多次研讨、调整、对比,尽可能确保主题框架的规范性、可行性,符合中国义务教育阶段数学课程的实际情况,完善教材分析的主题框架.为确保信效度,以上过程均采用双编码的方式由两人独立完成,并邀请3位数学教育专家参与,听取多方建议.
(2)主题追踪图的制定阶段.依据中国数学教材的实际情况,基于主题框架制定中国数学教材的主题追踪图,并采用多种方法确保研究的信效度.在预编码阶段,对结果的一致性、内容效度等进行量化的分析和检验.首先,所有参与分析的人员接受培训并通过考核.其次,依据同样的标准、步骤,在选定的4个版本教材中,各选择1册教材由两人同时编码,保证其一致性在0.9以上,否则再次讨论,直到达成一致.最后,如果仍然存在分歧,则由第三人即分析小组组长参与分析讨论,并判断决定.另外,在分析过程中,邀请3位数学教育专家多次对主题追踪图进行分析和修订,以保证主题追踪图的内容效度.
在正式编码阶段,首先,对4个不同版本的教材,从一~九年级逐一进行分析,每本教材以每一章中的每一个小节的具体内容为“单元”,分析、研讨其涉及的主题内容,并进行编码、记录,了解各个教材在年级上的主题分布情况;其次,针对分析过程中出现的问题或不确定情况,通过咨询数学相关领域专家意见等方式,研讨后达成一致;最后,进行修订、完善.
(3)主题追踪图的分析比较阶段.为便于分析比较,首先根据TIMSS A+的主题框架的顺序,对中国教材主题追踪图中主题的呈现顺序加以适当调整,并把中国教材中特有的几个主题放置在图中的最后位置.再依此对不同版本教材的主题追踪图深入分析,并与TIMSS A+的主题分布加以比较.
3 研究结果
3.1 主题概述
依据《课标》,结合TIMSS数学主题框架,尤其是TIMSS A+的主题分析框架,确定了共33个主题构成的主题追踪分析的框架,其中,覆盖了TIMSS A+的所有主题,同时也保留了《课标》中所规定的,但TIMSS A+主题框架中没有的主题.
由图1可见,总体来看,中国不同版本数学教材的主题框架都一致,这主要是中国的数学教材编写都是依据教育部颁布的《课标》,实行“一纲多本”的措施.而不同版本之间的差异,主要会出现在各个年级的主题覆盖上.进一步与TIMSS A+相比较,其所有主题均出现在中国不同版本教材中,但是,“探索规律”“图形与位置”“不等式与不等式组”“可能性与概率”是中国不同版本教材中所特有的主题.
3.2 主题分布的数量
从整体上看,国内多个版本教材各年级所涉及的主题数量,呈现出随年级的增加先增加后减少的趋势.不同版本教材主题数量变化情况如图2所示.具体来看,对于国内教材来说,一般从一年级的6~8个主题,逐步增加到四~六年级的14~19个主题,此时在主题的数量上达到高峰,后又在八~九年级逐步减少到每个年级学习7~12个主题.在不同版本教材中,主题数量排在前三的年级都有四~七年级.其中,版本2、版本3主题数量最多的是四年级,而版本1、4最多的是六年级.其中版本2、3、4从三年级到四年级的主题数量分别增加了10、7、6个,而版本1仅增加了2个主题.
在数与代数部分,国内不同版本教材的主题数量变化趋势一致,都是从一年级开始出现,一直持续到九年级.其中,版本3在四年级和七年级的主题数量较多,版本2在四年级和六年级的主题数量较多,版本1在四~七年级期间的数量比较均衡.TIMSS A+的教材在四~六年级的数量较多.在四年级以前,中国不同版本教材的主题数量高于TIMSS A+,而在四年级之后,TIMSS A+的教材主题则普遍高于中国不同版本教材.
TIMSS A+的主题数量随年级变化的趋势整体一致,在一~二年级的3个左右主题,逐步增加到五~六年级的20个左右的主题,并随后在七~八年级回落到17~18个主题.与国内教材相比较,四年级以前,中国的不同版本教材的主题数量高于TIMSS A+,而四年级之后,TIMSS A+的主题数量则普遍高于中国的不同版本教材.
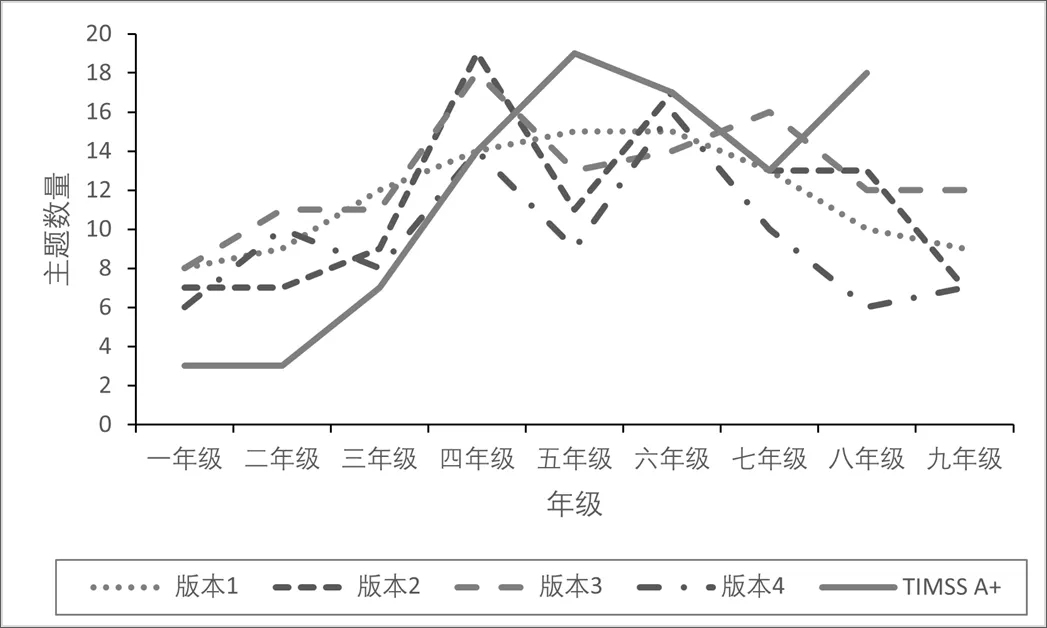
图2 不同版本数学教材主题数量随年级变化图
在图形与几何部分,版本3涉及的主题数量最多,在九年级包括8个主题,版本2在四年级和七年级同时达到主题数量高峰,各包括7个相关主题,其它版本的国内教材主题数量在2~6个之间分布.TIMSS A+的教材的该部分内容随年级逐渐增加,在八年级到达最高峰,包含9个主题.在六年级以前,中国不同版本教材的主题数量高于TIMSS A+,而在六年级及之后,TIMSS A+的教材主题则普遍高于中国不同版本教材.同时需要关注的是,中国各版本教材均在一~二年级就纳入4~5个主题,但TIMSS A+直到四年级才开始包括4个主题.
在统计与概率部分,由于这部分的主题数量较少,仅涉及数据表示与分析,可能性与概率两个主题,因此在不同版本教材中差异较小.不同版本的数据表示与分析的主题多于二~三年级开始介绍,其中版本1、2、3中均无间断持续到八年级.可能性与概率于四~五年级开始介绍,但TIMSS A+的教材中没有出现可能性与概率的主题.
3.3 主题分布的特点
已有研究和经验表明,严密性、连惯性和适切性等是课程教材设计中重要的思路和原则[23-24].深入分析国内各版本教材,并与TIMSS A+的主题分布比较,发现以下特点.
3.3.1 严密性
从严密性的角度来看,4套教材的知识内容分布总体而言比较类似,即低年级时主要关注基础性的知识内容,随着年级的增高,逐步开始关注更为抽象的、高级的数学知识内容.主题的分布体现出中国数学课程主题设计的整体思路.以数与代数领域为例,有关“整数的意义”和“整数的运算”主题,有2个版本的教材主要分布在一~四年级,2个版本的教材主要分布在一~六年级;“式与方程”有2个版本教材从四年级开始学习,2个版本从五年级开始,且都主要分布在七、八、九年级;“模式、关系与函数”,4个版本的教材都是分布在七、八、九这3个年级.可以看出,从一~九年级的主题内容逐渐扩充,抽象程度越来越高,解决的问题越来越复杂,其主题的分布:从数及数的运算到代数式及其运算,再到方程和解方程、函数.从数的扩充的角度看,从常量到变量;从关系的角度看,从数量关系的等量关系到不等关系、变化关系.在图形与几何领域,主题的分布也同样体现出内容抽象程度、问题复杂性,随年级逐渐增加的特点.总之,在义务教育阶段,中国数学内容主题在一~九年级作为一个整体系统来设计,结合学生的学习和发展需要,体现出不同学段/年级之间的一致和差异[25].
TIMSS A+主题分布的整体情况与中国类似,不同主题内容都呈现出先基础后深入的顺序,便于学生对知识的融会贯通.但是,也能看到在主题上有一定差异.在数与代数、图形与几何部分,中国教材都分别增加了“探索规律”“图形与位置”,并在一~六年级间的3个以上的年级出现.在统计与概率部分,中国教材增加了“可能性与概率”,而这一主题在TIMSS A+没有出现.另外,主题出现的顺序也存在一定差异.如在国内教材中,多边形与圆等主题与整数的意义/整数的运算同时出现,从一年级开始进行教学,而半数以上的TIMSS A+则到四年级才开始教学.在国内教材中,立体几何从一年级便开始涉及,而TIMSS A+在小学阶段并未涉及,而是在平面几何基础/多边形与圆/图形与变换都学习之后才开始接触.
3.3.2 连贯性
已有研究发现,主题的连贯学习(减少间断次数)符合学生的认知发展规律,能有效帮助学生加深理解和更好地掌握所学的知识技能[23].
主题分布的连贯性,即某个主题出现后无间断,直至学完为止.中国教材主题分布出现间隔的比例,4个版本的至少间隔1次的主题占比分别为30.3%、39.4%、48.5%和45.5%,其中,间断2次及以上的主题比例分别为9.1%、15.2%、12.1%和9.1%.进一步分析,国内版本教材中断较多的主题出现在分数、式与方程等数与代数领域,及几何基础、多边形与圆、周长面积与体积、图形变换、立体几何等图形与几何领域,且图形与几何领域出现更多中断情形.
而TIMSS A+涉及的主题中,除去有5个主题是在一个年级(其中4个主题在八年级)进行教学外,几乎所有主题内容都在年级间为连续,即不间断地分布,仅在数据表示与分析这一个主题上有1次间隔.
3.3.3 跨年级性
在TIMSS相关课程主题分布的研究中,研究者提出了跨年级性,发现高成就国家的主题分布具有较显著的跨年级特征.对于大多数主题内容来说,都在多个年级进行教学,其中50%以上的主题至少在3个年级及以上进行教学.国内4个版本教材中,3个年级及以上的主题所占比例分别为51.5%、57.6%、54.5%、39.4%,其中,相对而言,版本2跨3个年级的主题最多.仅在一个年级学习的主题占比,4个版本教材是24.2%、30.3%、21.2%和36.3%.此外各个主题的开始年级也越来越受到研究者关注[26].国内4个版本教材中也表现出一定差异,如“负数”,版本2和版本3的起始安排在四年级,版本4安排在五年级,而版本1安排在六年级.
TIMSS A+的教材中,3个年级及以上的主题所占比例为55.2%,国内仅有版本2的3个年级及以上主题占比超过这一比例,达到57.6%.考虑到TIMSS A+只分析到八年级,国内版本1、版本3、版本4的教材与TIMSS A+的差异更加凸显.而对于只在一个年级教学的主题的比例,TIMSS A+的平均比例为14.3%,而中国4个版本的比例均在21%以上.即同一主题在年级上的分布因教材的不同而不同,总体来看,中国4套教材主题的年级跨度小于TIMSS A+.
虽然在TIMSS相关课程主题分布的研究中提出了跨年级性,发现TIMSS A+的主题分布具有较显著的跨年级特征.但是主题的跨年级性的相关因素较多,不仅与主题的具体内容有关,也与主题划分的大小(详略)有关,还与学生的认知发展有关,主题分布的跨年级性,尤其是跨几个年级为好,还缺乏更多的理论和实证研究,值得进一步研究分析.同样,各个主题安排的起始年级的差异,“主要考虑是什么?”“是什么原因造成的?”“是否会对学生的学习带来影响?”“会有怎样的影响?”等问题,都还需要相关的研究,尤其是实证研究深入分析,探究其可能机制等.
4 结论与启示
4.1 结论
基于中国不同版本数学教材的主题追踪图,可得出如下结论:(1)中国不同版本数学教材覆盖的主题均一致,主题数量随年级的变化趋势一致;(2)不同版本数学教材的主题安排都体现出从基础到高级的变化特点;(3)4个版本教材中有间断的主题比例均较高;(4)4个版本教材主题分布均具有一定的年级跨度;(5)4个版本教材中部分主题的起始年级存在明显差异.
进一步分析,根据中国数学教材和TIMSS A+的主题内容和分布的比较,发现:(1)在主题内容上,中国不同版本教材与TIMSS A+基本一致,但是,有个别主题是我国教材特有;(2)相比TIMSS A+的课程内容分布模式,中国各版本教材的主题所出现的年级总体更小;(3)中国教材在内容连续性上,和TIMSS A+有一定差异,TIMSS A+的主题连续性明显更好;(4)相比而言,中国各版本教材的总体年级跨度更小,教学内容分布更为集中.
4.2 启示
主题内容的科学合理选择是课程与教学中最为基础和核心的问题之一.研究发现中国数学教材的主题内容涵盖了TIMSS A+的主题,有个别主题是中国教材所特有的.这一结果与已有仅针对图形与几何的知识内容比较研究的结果类似[27].这可能与不同国家的数学教育发展情况有关,也与中国数学课程标准不断修订完善有关.主题内容的选择需考虑多方因素,如课程主题需要及时更新以保持与社会发展同步,内容选择要体现教育目标和理念等.此外,知识内容数量的确定也需要不断权衡,既要保障每个知识点足够的教学时间,也要避免学生的知识面太过狭窄而影响对学科的整体把握和知识点间的融会贯通[28].特别是目前国际国内都关注学生课业负担、提倡减负的情况下,课程内容数量的选择更应引起研究者的重视.
主题内容的组织直接影响教师“教”和学生“学”[29].研究发现,中国数学教材的主题安排呈现从基础到高级的渐进过程,但是在主题分布的连贯性、年级跨度上与TIMSS A+还有一定的差异.这一结果与已有研究关于中外小学教材的比较结果基本一致[17,30],但已有研究仅涉及到一~六年级,缺乏对整个义务教育阶段的教材情况的比较,尚不明确这一阶段的教材总体特点.整体来看,教材内容组织应充分考虑到各知识点之间的内在逻辑和关联[31],同时也需要考虑义务教育阶段学生能力发展的阶段性特点,以明确不同知识点和发展阶段的相互影响.在内容组织上,需遵循主题聚焦、内容严谨和挑战性等的组织原则,即对于重点知识要有足够的内容呈现深度,充分考虑到学生认知发展的不同水平和知识主题掌握的先后顺序[32],也要具有一定的挑战性,有助于学生的深入学习和反思,提升他们解决问题的能力[33].
教材编写和教材研究具有重要作用.中国数学教材的编写在《课标》的指导下进行,但是《课标》并没有明确要求到各个具体的年级.研究发现,中国4个不同版本的教材在整体主题数量、分布等方面都具有较好合理性、一致性,但具体到各个年级仍然存在一定的差异.已有研究也提出数学教材中整体设计的必要性,需注重学习内容之间的关系,强调小学到高中各阶段内容的一体化设计,注重深度整合联系,为学生提供顺畅科学的数学学习体系[31,34].教材编写关系到课程体系质量的高低,离不开相关的理论和研究作为其重要依据[35].如教材内容选择、知识点数量、内容组织和呈现形式等问题都是在课程研究中亟需回答的问题,但相对缺少实证研究[36].围绕课程和教材开展更多实证研究[34],可以弥补中国在这方面研究的相对不足,提升中国课程和教材设计的科学性、合理性[37],为教材编写提供更多重要的依据和参考,更好服务于学生的教育发展.
4.3 研究不足和展望
研究还存在一些不足和待改进之处:(1)在主题的设计上,还可以更多考虑中国数学课程的自身特点,细化主题的划分;(2)在教材的选取上,除了目前的4个版本外,还可以考虑其它不同的版本教材;(3)在TIMSS A+的主题分布上,还可以追踪其变化趋势等信息;(4)在分析方法上,还可以尝试更多的质性和量化结合的思路和方法.总之,以上几点都值得进一步完善和深入,在借鉴主题追踪图的研究思路和范式基础上,通过相关的实证研究,为中国义务教育数学课程和教学改进提供更多的参考依据.
[1] COGAN L S, SCHMIDT W H, WILEY D E. Who takes what math and in which track? Using TIMSS to characterize US students’ eighth-grade mathematics learning opportunities [J]. Educational Evaluation and Policy Analysis, 2001, 23 (4): 323-341.
[2] VALVERDE G A, BIANCHI L J, WOLFE R G, et al. According to the book: Using TIMSS to investigate the translation of policy into practice through the world of textbooks [M]. Dordrecht: Springer Science & Business Media, 2002: 4-11.
[3] 曹一鸣,吴立宝.初中数学教材难易程度的国际比较研究[J].数学教育学报,2015,24(4):3-7.
[4] 王攀峰.教科书研究方法的现状、问题与建议[J].课程·教材·教法,2017,37(1):34-41.
[5] 余宏亮.建设教材强国:时代使命、主要标志与基本路径[J].课程·教材·教法,2020,40(3):95-103.
[6] 韩震.教材编写的意识形态维度[J].课程·教材·教法,2019,39(7):9-13.
[7] 何卫国,巩子坤.数学教材研究综述:问题,方法与框架[J].枣庄学院学报,2012,29(6):79-84.
[8] 徐玉庆.数学教材研究:范式的角度[J].教育导刊,2017(2):49-53.
[9] 姜天卓,李淑文,秦德生.学生使用数学教科书的国际研究现状与趋势——基于WOS数据库的HistCite计量分析[J].数学教育学报,2023,32(1):66-72.
[10] SCHMIDT W H. TIMSS curriculum analysis: Topic trace mapping [J]. Prospects, 1992, 22 (3): 326-333.
[11] MURDOCK J. Comparison of curricular breadth, depth, and recurrence and physics achievement of TIMSS population 3 countries [J]. International Journal of Science Education, 2008, 30 (9): 1 135-1 157.
[12] MESA V, SUH H, BLAKE T, et al. Examples in college algebra textbooks: Opportunities for students’ learning [J]. Primus, 2012, 23 (1): 76-105.
[13] VALVERDE G A. Curriculum convergence in Chile: The global and local context of reforms in curriculum policy [J]. Comparative Education Review, 2004, 48 (2): 174-201.
[14] FAN L, ZHU Y, MIAO Z. Textbook research in mathematics education: Development status and directions [J]. ZDM, 2013, 45 (5): 633-646.
[15] 姜浩哲,沈中宇,邹佳晨.中美基础教育数学课程发展:比较与启示——蔡金法教授访谈录[J].数学教育学报,2023,32(3):56-63.
[16] 张新宇,袁智强,占小红.课程内容研究的新视野——TIMSS课程分析工具“主题追踪图”的演进与启示[J].比较教育研究,2011,33(1):76-80.
[17] 王烨晖,辛涛,边玉芳,等.TIMSS视角下我国小学数学目标课程的比较研究[J].课程·教材·教法,2012,32(4):92-97.
[18] 钟启泉.一纲多本:教育民主的诉求——我国教科书政策述评[J].教育发展研究,2009,29(4):1-6.
[19] 郑振兴.中国初中数学教材中无理数内容编写特点研究[J].数学教育学报,2023,32(3):39-43.
[20] 薛理银,顾明远.比较教育导论:教育与国家发展[M].北京:人民教育出版社,1998:29-32.
[21] 卢丽华,孙新洋.当前我国教材研究的特点及趋势——基于CSSCI期刊收录文献的可视化分析[J].中国教育技术装备,2020(12):59-63.
[22] SCHMIDT W H, MCKNIGHT C C, VALVERDE G, et al. Many visions, many aims: A cross-national investigation of curricular intentions in school mathematics [M]. Dordrecht: Springer Science & Business Media, 1997: 197-206.
[23] SCHMIDT W H, WANG H C, MCKNIGHT C C. Curriculum coherence: An examination of US mathematics and science content standards from an international perspective [J]. Journal of Curriculum Studies, 2005, 37 (5): 525-559.
[24] OECD. International curriculum analysis: Twenty years of background analyzing mathematics and science curricula [M]. Paris: OECD Publishing, 2016: 6-7.
[25] 刘鹏飞,史宁中,孔凡哲.义务教育数学课程学段划分的国际比较研究[J].外国中小学教育,2012(3):49-53.
[26] OECD. Curriculum (re)design [M]. Paris: OECD Publishing, 2020: 29-30.
[27] 张玉环,吴佳桧.知识与核心素养视角下中法图形与几何比较研究——基于法国2018版与中国2011版义务教育课程标准[J].数学教育学报,2022,31(1):70-78.
[28] 唐恒钧,张维忠.教师教育类课程的教材:注重方法与理性实践——以《中学数学课程标准与教材研究》为例[J].数学教育学报,2015,24(2):57-60.
[29] WIJAYA A, van den HEUVEL-PANHUIZEN M, DOORMAN M. Opportunity-to-learn context-based tasks provided by mathematics textbooks [J]. Educational Studies in Mathematics, 2015, 89 (1): 41-65.
[30] 俞蓉,赵世恩.中英小学数学教材中“图形的运动”难度比较研究[J].数学教育学报,2022,31(6):80-86.
[31] 章飞,安志军,顾继玲,等.数学教科书学习内容整体设计外显的“必要性”“内容”与“方法”[J].数学教育学报,2022,31(5):59-64.
[32] LEE S, SO K. Analysis of change trends on OECD’s competencies frameworks for curriculum redesign: Focused on “Education 2030” [J]. The Journal of Curriculum Studies, 2019, 37 (1): 139-164.
[33] OECD. Curriculum overload: A way forward [M]. Paris: OECD Publishing, 2020: 85-88.
[34] 王思凯,李沐慧,徐斌艳.国际视野下数学教材研究的行动与展望——基于ICME-14数学教材研究的分析[J].数学教育学报,2022,31(3):15-19.
[35] 王建波.美国CM数学教材统计内容编写特点及其启示[J].数学教育学报,2015,24(2):30-34.
[36] 范良火,吴立建.国际数学教材研究和发展趋势述评和分析——从首届国际数学教材研究和发展会议及其大会报告说起[J].数学教育学报,2015,24(3):1-5.
[37] 郑毓信.《义务教育数学课程标准(2022年版)》的理论审思[J].数学教育学报,2022,31(6):1-5.
Comparison of Topic Distribution in Multiple Versions of Mathematics Textbooks: Topic Trace Mapping
YANG Tao, YANG Jian-qiang, WANG Ye-hui, JIA Chao-chao, TAN Yu-ting
(Collaborative Innovation Center of Assessment for Basic Education Quality, Beijing Normal University, Beijing 100875, China)
Textbooks are an important part for teaching and studying. Based on the TIMSS topic trace mapping method, this study analyzed four different versions of mathematics textbooks in compulsory education and compared them withthe topic distribution of TIMSS high-achieving countries and regions (TIMSS A+). The results show that: (1) The overall trend of the number of topics in the four different versions of mathematics textbooks changed with grades.Andthe topic contents all reflected the gradual process from basic to advanced. The proportion of topic distribution with discontinuities was between 30.3% and 48.5%. The topics across three grades and above accounted for 39.4% to 57.6%. (2) Compared with TIMSS high-achieving countries and regions, China’s mathematics textbooks have slightly more topics. Specifically, the number of topics that appear before grade 4 was much more in China and the consistence of topics was obviously worse than that of TIMSS A+. Besides, the average grade span of topics is smaller in China. The findings provide implications for the topic selection, content organization, textbook compilation and related research on mathematics textbooks in China.
mathematics textbooks; topic trace mapping; topic distribution
G623
A
1004–9894(2024)01–0071–06
杨涛,杨建强,王烨晖,等.义务教育不同版本数学教材主题分布比较:基于主题追踪图的研究[J].数学教育学报,2024,33(1):71-76.
2023–10–08
北京市教育科学“十三五”规划2017年重点课题——义务教育阶段数学课程测量:基于主题追踪图的应用研究(CADA17079)
杨涛(1967—),女,四川成都人,副教授,博士生导师,主要从事教育测量与评价研究.杨建强为本文通讯作者.
[责任编校:陈隽、陈汉君]
