迭代学习控制器参数的数据驱动自适应整定方法

于瀛祯,林 娜,池荣虎

(青岛科技大学 自动化与电子工程学院,山东 青岛 266061)

自从迭代学习控制(iterative learning control,ILC)在1984年被ARIMOTO 提出之后[1],目前已经取得了许多理论成果[2-4]和成功应用[5-7]。ILC的核心思想就是利用上一次迭代的控制输入和跟踪误差对当前迭代的控制输入进行修改,从而使输出随着迭代次数的增加能够很好地实现对期望轨迹的跟踪。

PID 型ILC 包 括P 型ILC、PD 型ILC、PID 型ILC等多种组合形式,具有易于实现、具备良好跟踪性能等诸多优点。在文献[8]中,提出了一种改进的PD 型ILC 方法,所提方法具有良好的瞬态响应。在文献[9]中,针对具有时变不确定性的工业间歇过程,提出了一种鲁棒PI型ILC 方案。在文献[10]中,提出了一类具有初始学习状态的单边Lipschitz非线性系统的开环和闭环P型ILC 算法。然而,传统的PID 型ILC 的控制器增益一旦被选中就会被固定,当外部环境因为扰动或者不确定性而发生变化时,这些固定增益的控制器可能无法适应这些变化,从而导致系统控制性能变差。因此,如何动态地调整PID 型ILC 的学习增益引起了学者们的广泛关注。文献[11]提出了一种利用遗传算法来选择PID 型ILC 学习增益的方法。但是遗传算法中涉及到许多参数,这些参数大多数是需要根据经验选择的。在文献[12]中,作者采用粒子群优化算法对自适应PID 型ILC进行研究。然而,用粒子群算法来选择控制增益是非常复杂繁琐的。文献[13]设计了一种模糊PID 型ILC的方法,该方法的基本思想是利用模糊控制来设置PID 参数从而抑制未知因素带来的影响。但是如何选择一个合适的模糊隶属函数通常不是一件容易的事。

近些年,一些自适应迭代学习控制(adaptive iterative learning control,AILC)方法[14-17]被提出。这些AILC方法的核心思想就是通过引入参数自适应控制律从而实现学习过程中参数的自适应调节。在文献[14]中,作者利用参数估计律中的对齐条件,直接将传统的自适应控制方法引入到ILC 任务中去。文献[15]通过将迭代轴和离散时间轴类比,从而提出了一种新的AILC方法。文献[16]提出了一种同时处理非线性系统迭代变化初始误差和参考轨迹的AILC方法。然而,上述这些AILC 方法都是建立在模型信息已知的情况下,如果模型信息未知,那么这些方法在实际应用中将很难实现。

针对上述非线性系统的AILC设计和分析遇到的依赖系统模型信息的问题,可以采用神经网络或者模糊算法对未知的非线性函数进行逼近。文献[18]提出了一种适用于不确定非线性系统的自适应模糊迭代学习控制器设计方法。文献[19]提出了一种用高阶神经网络来设计非仿射离散时间系统的AILC方法。然而,这些方法存在着另一个问题:在实际应用过程中选择合适的神经网络或模糊隶属函数通常是不容易的。

文献[20]提出了一种迭代动态线性化(iterative dynamic linearization,IDL)方法。该方法仅考虑当前迭代的信息,将一个离散时间非线性非仿射系统转化为一个等价的线性数据模型,称为紧格式迭代动态线性化。此外,在文献[21]中,IDL技术被用来处理一个理想的非线性迭代学习控制器,并利用更多以往迭代的信息提出了面向控制器的偏格式动态线性化方法。这里值得指出的是,IDL 方法不需要任何数学模型的先验信息,是一种数据驱动的方法。同时,相较于神经网络和模糊系统,IDL 方法不需要经过训练过程就可以得到线性数据模型。

基于上述分析,本研究针对非线性非仿射系统,提出了两种PID 型ILC 的DDAT 方法。首先,提出了一种具有可变增益的PID 型ILC律,其增益都是未知且需要估计的。然后,基于CFIDL得到的线性数学模型,设计了一个新的目标函数来估计学习增益的变化。在此基础上,通过优化目标函数,提出了一种基于CFIDL 的DDAT 方法。进一步,利用PFIDL技术对结果进行推广,得到了一种基于PFIDL 的DDAT 方法。最终,通过仿真验证了所提方法的有效性。

1 问题描述

考虑如下所示的单输入单输出非线性系统:

其中,ui(t)∈R和yi(t)∈R分别表示第i次迭代t时刻的控制输入和输出;t∈［0,T］,T是一个正整数;i∈［0,+∞）;f(·)表示未知的非线性函数,ny和nu是未知的正整数。

首先,对系统(1)给出了如下两个假设:

假设1f(·)函数关于控制输入ui(t)具有连续的偏导数。

假设2对于任意的i∈［0,+∞）,t∈［0,T］,如果,那么系统(1)满足广义Lipschitz条件,即:

其中,b1是一个正常数,Δ 是一个迭代差分算子,即Δai(t)=ai(t)-ai-1(t)。

引理1[20]对于满足假设1 和假设2 的系统(1),当Δui(t)≠0,一定存在一个时变参数φi(t)可以将系统(1)转化为如下等价的线性数学模型:

其中,φi(t)是一个未知参数,且满足

接下来,考虑一个准则函数:

然后,将准则函数(3)对φi(t)求偏导,并令其为0,可以得到(t)的参数更新律:

其中,η∈（0,1］是一个步长因子。

通过参考文献[20],为了使参数更新律(4)具有更好的跟踪性能,引入了一种如下所示的重置算法:

其中,(t)是(t)的初始值;ε是一个足够小的正常数。

2 基于CFIDL的DDAT

本研究采用如下形式的PID 型ILC律:

其中,ψi(t),ζi(t)以及Γi(t)是3个需要估计的动态学习增益;跟踪误差定义为ei(t+1)=yd(t+1)-yi(t+1),其中yd(t+1)是被控系统的期望输出。在此基础上,控制律(6)可以改写为如下形式:

本节的目的是设计一种基于CFIDL 的DDAT方法,使跟踪误差ei(t+1)在迭代次数i趋近于无穷时渐近收敛到零

接下来,设计一个如下所示的目标函数:

其中,αc＞0,χc＞0以及βc＞0都是权重因子;ρc是一个足够小的正常数。ei(t+1)表示系统的跟踪误差以 及分别表示控制器的比例增益,积分增益,微分增益的估计值。

然后,结合表达式(2),控制律(7)以及跟踪误差的定义式,可以得到如下所示的表达式:

把新得到的误差表达式(9)代入到目标函数(8)中得到一个新的目标函数,然后将新得到的目标函数表达式对(t)求偏导,并令其为0,可以得到:

接下来,将等式(9)代入到等式(8)中,然后将得到的新表达式对(t)求偏导,并令其为0,可以得到:

综上所述,所提出的基于CFIDL 的DDAT 方法总结如下:

其中,B3＞并且是一个足够小的正常数;(t)是(t)的初始值;B4＞并且是一个足够小的正常数(t)是(t)的初始值;B5＞并且是一个足够小的正常数;(t)是(t)的初始值。式(17)、(19)和(21)是3个重置算法,它们的作用是为了限制比例增益、积分增益以及微分增益的范围,从而提高估计算法(16)、(18)和(20)的有效性。

注1与传统的固定增益的PID 型ILC方法相比,所提出的DDAT 方法可以利用I/O 数据对学习增益进行自适应调整,使ILC 方法对不确定性具有更强的鲁棒性。

注2与文献[14-17]提出的AILC方法以及文献[18-19]提出的基于神经网络和模糊方法的ILC方法相比,所提出的方法是数据驱动的,摆脱了对系统机理模型的依赖,因此更适用于模型复杂或者难以建模的实际应用。

为了表述的更加清晰,在图1 中给出了基于CFIDL的DDAT 方法的框图,其中z-1表示一个时间滞后算子。

图1 基于CFIDL的DDAT方法框图Fig.1 Block diagram of CFIDL based DDAT method

3 基于PFIDL的DDAT

3.1 问题描述

首先针对非线性系统(1)提出如下两个假设:

假设3f(·)函数对于第i个到第(i-L+1)个变量具有连续的偏导数,其中L是一个正整数。

假设4对于任意的i∈［0,+∞）,t∈［0,T］,如果‖ΔUi(t)‖≠0,那么系统(1)满足广义Lipschitz条件,即。其中,Ui(t)=［ui(t),ui-1(t),…,ui-L+1(t)］T,表示所有的控制输入信号都包含在一个长度为L的输入向量Ui(t)内。

引理2对于满足假设3和假设4的系统(1),当‖ΔUi(t)‖≠0,一定存在一个时变向量φi(t)可以等效地将系统(1)转化为以下线性数学模型:

证明

根据假设3和柯西中值定理可以得到:

随着时代变迁、生活方式改变、饮食结构调整，高尿酸血症已经成为继高血压、高血糖、高血脂之后出现的第四高，但由于高尿酸血症早期多无明显临床症状而不被人们重视。越来越多的研究表明，高尿酸血症不仅是痛风和肾结石的前期病变，而且与血脂代谢紊乱、肥胖和高血压等疾病在遗传和病理机制上有密切的联系，高尿酸血症可与肥胖、高血压、高脂血症、糖耐量异常等发生协同作用，加重动脉粥样硬化，促进心脑血管疾病的发生[1-3]。本研究对52 673名体检人群资料进行统计分析，以了解体检人群中血清尿酸水平并探索其与心血管病危险因素（超重与肥胖、高血压、糖尿病、血脂异常）之间的关系，为高尿酸血症及心血管病防治提供客观依据。

接下来,考虑如下含有向量υi(t)的方程:

因为‖ΔUi（t）‖≠0,所以方程(24)一定存在一个如下形式的解(t):

基于等式(23)～(25),可以得到Δyi(t+1)=(t)ΔUi(t),引理2证毕。

根据假设4和引理2可以得到‖φi（t）‖≤b2。因此,φp(t)=i,…,i-L+1 也是有界的,定义,其中是一个正常数。

接下来,考虑如下所示的准则函数:

其中,μp＞0是一个权重因子(t)是φi(t)的估计值。

将准则函数(26)对φi(t)求偏导,并令其为0,可以得到:

为了使参数更新律(27)具有更好地跟踪时变参数的能力,引入如下所示的重置算法:

其中,ε是一个足够小的正常数(t)是(t)的初值。

3.2 控制器设计

在这里采用的是与之前相同的PID 型ILC律:

然后,设计一个如下所示的目标函数:

其中,αp＞0,χp＞0以及βp＞0都是权重因子;ρp是一个足够小的正常数。ei(t+1)表示系统的跟踪误差以 及分别表示控制器的比例增益,积分增益,微分增益的估计值。

根据等式(22)和跟踪误差的定义式,可以得到:

更进一步,根据控制律(29)和ΔUi t（）的定义式,可以得到:

结合式(29)、(31)和(32),可以得到:

将得到的新误差表达式(33)代入到目标函数(30)中,然后将得到的新目标函数表达式对(t)求偏导,并令其为0,可以得到:

同理,可以得到(t)和(t)的更新律:

综上所述,所提出的基于PFIDL 的DDAT 方法总结如下:

注3与基于CFIDL的DDAT 方法相比,基于PFIDL的DDAT 方法在学习规律中包含了更多的附加控制知识,使被控系统对于不确定因素具有更强的鲁棒性,可以有效地提高控制性能。此外,由于考虑了更多的前批信息,使得基于PFIDL的DDAT方法的控制器变得复杂,会给收敛性分析带来一定的困难。

4 实验仿真与结果分析

将通过一个数例仿真来验证所提出的两种算法的有效性。

考虑如下所示的一个非线性非仿射系统:

其中,t∈ ［0,200］。控制输入和输出的初值为u0(t)=0,yi(0)=0.5。

参考轨迹定义如下:

为了模拟实际的外部干扰,在仿真中考虑了如图2所示的随机扰动di(t)=0.03rand(1)。

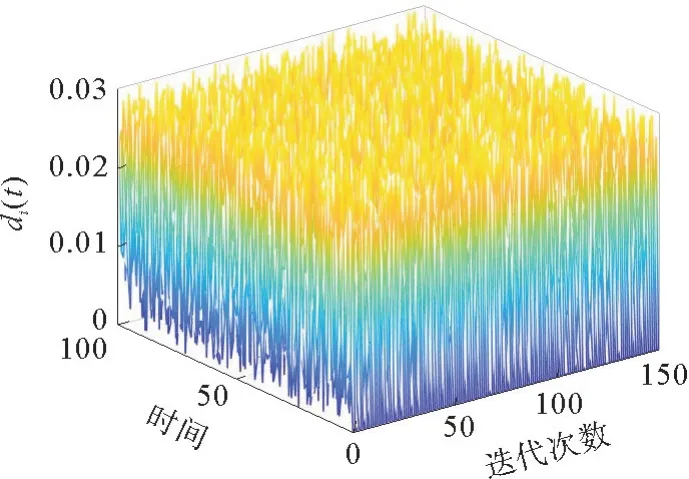
图2 随机扰动Fig.2 Random disturbances

为了验证所提出的基于CFIDL的DDAT 方法的有效性,将其与传统的ILC 方法进行了比较。考虑的传统PID 型ILC的控制律如下所示:

通过试凑法设定传统PID 型ILC 的增益为KP=0.268,KI=0.163,KD=0.3。为了公平起见,将所提出基于CFIDL的DDAT 方法的初始学习增益设为与传统PID型ILC方法所选增益相同的值,即(t)=0.268(t)=0.163,(t)=0.3。其他控制器的参数设置如下:αc=10-4,χc=10-4,βc=10-4,μc=10,η=0.6(t)=0.005,ρc=ε====10-7=0.9,B3=0.6,B4=0.3,B5=0.5。

在图3和图4中,给出了仿真结果。图3表示系统输出的跟踪性能,用蓝色虚线表示系统实际输出,红色实线表示参考轨迹。图4分别用蓝色实线和红色虚线来表示基于CFIDL的DDAT 方法和传统的PID 型ILC方法下系统的跟踪误差,其中横轴表示迭代次数,纵轴表示系统的最大跟踪误差。从图3 和图4中可以看出,基于CFIDL的方法可以很好地保证系统输出跟踪误差沿迭代方向的收敛性,且收敛速度明显优于传统的PID 型ILC方法。

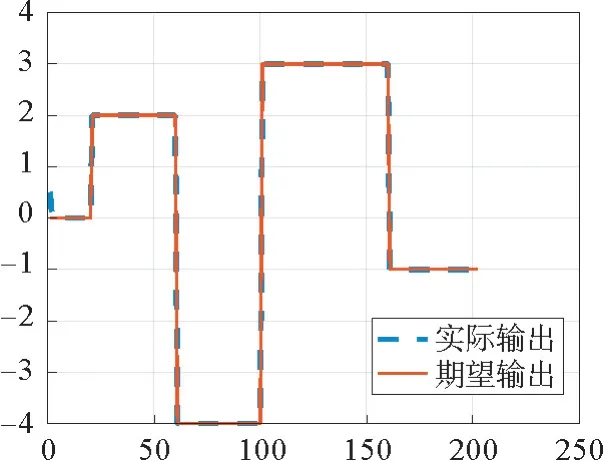
图3 系统输出描述Fig.3 Profile of system output

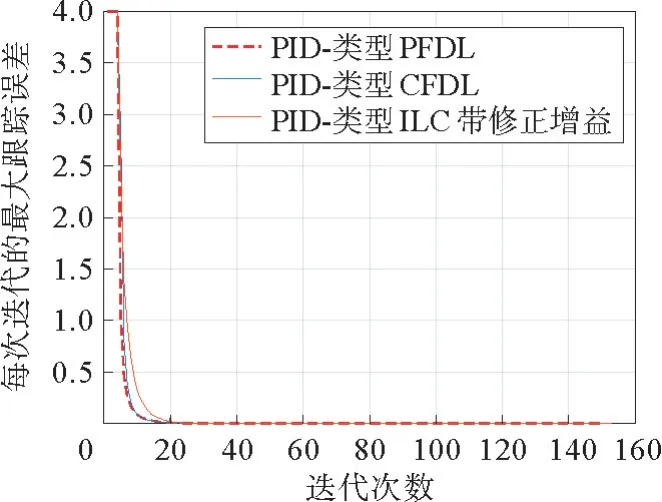
图4 跟踪误差的迭代收敛性Fig.4 Iterative convergence of tracking errors

更进一步,设置控制器参数为:L=3,αp=10-4,χp=10-4,βp=10-4,μp=10,ρp=ε=γψ=γζ=γΓ=10-7=0.9,=0.9,b3=0.6,(t)=［0.005 0.005 0.005］T,b4=0.3,b5=0.5,=0.6(t)=0.268,(t)=0.163,(t)=0.03。采用基于PFIDL的DDAT 方法的仿真结果如图4红色虚线所示。从图4 可以看出,所提出的基于PFIDL的DDAT 方法相比于所提出的基于CFIDL的DDAT 方法具有更好的控制效果。

5 结语

本研究提出的两种DDAT 方法都可以根据实际I/O 数据动态调整控制器的学习增益,从而有效提高系统对于不确定性的鲁棒性。通过数学分析和仿真验证了所提方法的有效性。一般来说,利用更多的数据信息可以获得更好的控制性能。因此,在对控制输入进行更新时,还可以考虑前一次迭代的输出信息,从而进一步提高控制性能,这些将在今后的工作中进行。