基于国密SM2算法的局部可验证聚合签名算法研究

沈荣耀 马利民 王佳慧 张 伟

1(北京信息科技大学北京未来区块链与隐私计算高精尖中心 北京 100101)

2(北京信息科技大学计算机学院 北京 100101)

3(北京信息科技大学国家经济安全预警工程北京实验室 北京 100101)

4(国家信息中心信息与网络安全部 北京 100045)

数字签名是一种可以有效保障网络安全的密码技术,广泛应用于我国政府、金融、商业等领域.在实际场景中,会持续产生海量的数字签名,占据大量存储空间,且对签名逐个验证会带来较大计算开销,因此,如何提高海量签名的验证效率,降低签名存储占用显得尤为重要.

由于聚合签名(aggregate signature, AS)可以提高批量验证效率,降低存储占用,所以尤其适用于解决大量签名的存储以及验证的问题.聚合签名由Boneh等人[1]于2003年首次提出.然而,对聚合签名验证时,验证方需要获取完整明文集合,当聚合的签名数量较多时,验证聚合签名所需明文数量也随之增大.有时验证方仅需验证指定明文,获取完整明文集合会为验证方增加计算负担.针对这种情况,采用局部可验证的聚合签名可以大大降低验证方的计算负担.局部可验证的聚合签名由Goyal等人[2]首次提出.

SM2算法[3]由国家密码管理局于2010年底发布,是一种基于椭圆曲线的密码算法,其具有自主可控、安全性高、易于实现等优点,广泛应用于各类信息系统之中.

本文提出一种安全、高效的基于国密SM2的局部可验证聚合签名方案.方案采用聚合签名技术,提高批量验证效率,同时采用局部可验证技术,使验证方对聚合签名及指定明文验证时,无需获取全部明文,仅需短提示即可,进一步降低验证方计算成本.

1 相关工作

根据采用的公钥密码体制,聚合签名可以划分成3类:基于身份的聚合签名(identity-based aggregate signature, IBAS)、无证书聚合签名(certificateless aggregate signature, CLAS)以及基于公钥基础设施(public key infrastructure, PKI)的聚合签名.

1) 基于身份的聚合签名:2006年,Gentry等人[4]提出一种高效的IBAS方案,然而该方案需要所有签名者共享状态信息,使应用场景受到限制;2007年,Boldyreva等人[5]提出有序IBAS方案,克服了Gentry方案的共享问题;2016年,Muranaka等人[6]改进了Boldyreva方案,针对动态源路由协议提出有序IBAS方案,该方案相较于Boldyreva方案,计算性能明显提高;2019年,Kojima等人[7]在Muranaka方案基础上进行改进,引入分布式密钥生成中心(key generation center, KGC),消除集中式KGC;2020年,安涛等人[8]针对车辆自组织网(vechicular adhoc network, VANET)提出一种基于国密SM9算法的IBAS方案,然而该方案聚合签名长度和签名车辆数量呈线性相关,导致通信开销较大.基于身份的聚合签名虽然性能较好,但是其密钥生成必须借助可信第三方,导致密钥托管的问题无法避免.

2) 无证书聚合签名:2018年,Kumar等人[9]针对医疗无线传感器网络(healthcare wireless sensor networks, HWSNs)构造CLAS方案,该方案计算开销小于其他同类方案;2019年,Kumar等人[10]针对VANET,在其之前方案[9]上构造CLAS方案,通过伪身份实现车辆的隐私保护;2022年,蒙彤等人[11]针对HWSNs提出支持并行密钥隔离CLAS方案,有效降低HWSNs系统的延迟.无证书聚合签名方案中部分私钥由半可信的第三方生成,另一部分私钥由用户自身产生,所以消除了密钥托管问题.当前大部分CLAS方案中都基于双线性对,导致效率较低,实用性较差.

3) 基于公钥基础设施的聚合签名:2019年,Verma等人[12]针对医疗监控提出无配对的基于证书的AS方案,然而该方案存在聚合签名长度与签名者数量呈线性相关的问题;同年,Verma等人[13]提出另一种基于证书的AS方案,该方案聚合签名更为紧凑;2021年,Verma等人[14]针对物联网环境提出无配对的基于证书的短聚合签名方案,计算开销更小;同年,Zhu等人[15]分析文献[14]方案安全缺陷,针对无线医疗传感器网络提出一种支持用户匿名保护的基于证书的AS方案并证明其安全性.基于公钥基础设施的聚合签名需要对证书的管理付出一定的代价,由于PKI已经广泛应用于各种现实场景中,因此基于PKI的聚合签名可以更好地与已部署的公钥基础设施相结合.

2022年,Goyal等人[2]针对验证者验证指定明文和聚合签名时,仍需获取完整明文集合的问题,提出局部可验证聚合签名的概念.验证方对聚合签名验证时,无需完整明文集合,仅需指定消息及对应短提示即可,并给出基于RSA以及双线性对的2种局部可验证聚合签名构造方案,并证明其安全性.

2 基于SM2的局部可验证聚合签名方案

本文基于聚合签名和局部可验证签名的思想,对SM2算法进行适当的改造,提出了一种基于国密SM2算法的局部可验证聚合签名方案(locally verifiable aggregate signature scheme based on SM2, SM2-LVAS).形式化地表示为SM2-LVAS=(Setup,Key-Gen,Sign,Verify,Aggregate-Signature,Aggregate-Verify,Local-Open,Local-Aggregate-Verify),算法共8个步骤.

2.1 系统建立

定义大素数p,Fp为有限域,a,b∈Fp为椭圆曲线E的参数,椭圆曲线上的基点(x,y),其中x,y∈Fp,n为群G的阶,Hv()为摘要长度为v(单位为b)的哈希算法.

2.2 密钥生成

SM2算法密钥生成流程如下:

1) 选取随机数d,并且d∈[1,n-2];

2) 计算P=dG,则其公私钥对为(P,d).

2.3 单个SM2签名

假设签名者为A,其公私钥对为(PA,dA),对于待签名消息Mi,随机选取ki∈[1,n-1].

1) 计算ZA=H256(ENTLA‖IDA‖a‖b‖xG‖yG‖xA‖yA),其中IDA为用户可辨识标识,ENTLA为IDA长度转化而成的2B数据;

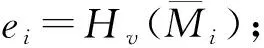
4) 计算(xi,yi)=kiG;

5) 计算ri=(ei+xi) modn;

6) 计算si=((1+dA)-1·(ki-ridA)) modn;

7) 计算vi=(ei+yi) modn.

单个签名为(ri,si,vi).

2.4 单个SM2验签

对收到的消息Mi及其数字签名(ri,si,vi)进行验签,其过程如下:

1) 检验ri,si,vi∈[1,n]是否成立,若不成立,则验证不通过;

2) 计算ZA=H256(ENTLA‖IDA‖a‖b‖xG‖yG‖xA‖yA);

5) 计算ti=(ri+si) modn;

6) 计算(xi,yi)=siG+tiPA;

7) 计算R′=(ei+xi) modn.

检查R′=ri是否成立,成立则验证通过,否则失败.

2.5 签名聚合

消息集合{M1,M2,…,Mi,…,ML}的数字签名为{(r1,s1,v1),(r2,s2,v2),…,(ri,si,vi),…,(rL,sL,vL)}.签名聚合过程如下:

1) 计算E=Hv(e1‖e2‖…‖eL);

2) 计算xi=(ri-ei) modn;

3) 计算yi=(vi-ei) modn;

5) 计算R=(E+x) modn;

7) 计算ti=(ri+si) modn;

聚合签名为σ=(R,U,W,t1,t2,…,tL).

2.6 聚合验证

验证方收到消息集合{M1,M2,…,Mi,…,ML}和聚合签名σ.聚合验证过程如下:

2) 计算ZAi=H256(ENTLAi‖IDAi‖a‖b‖xG‖yG‖xAi‖yAi);

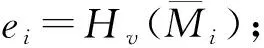
5) 计算d=Hv(e1‖e2‖…‖eL);

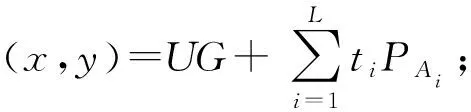
7) 计算R′=(d+x) modn.

当签名者相同时,椭圆曲线上的点(x,y)的计算可简化为(x,y)=UG+WPA.

检查等式R′=R是否成立,若成立则验证通过,否则验证失败.

2.7 提示生成

提示生成算法一般由存储服务器或签名聚合方进行计算.通过消息明文集合计算得到指定消息的短提示auxj.提示生成过程如下:

1) 计算ZAi=H256(ENTLAi‖IDAi‖a‖b‖xG‖yG‖xAi‖yAi);

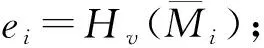
4) 计算E=Hv(e1‖e2‖…‖eL);

5) 计算auxj1=(E-ej) modn;

6) 计算h1=Hv(auxj1);

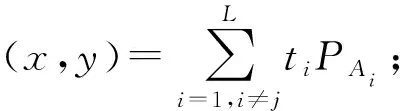
8) 计算auxj2=(h1+x) modn;

9) 计算auxj3=(h1+y) modn;

10)输出短提示auxj=(auxj1,auxj2,auxj3).

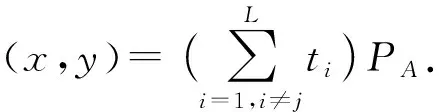
2.8 局部验证

验证方收到指定消息明文Mj、聚合签名σ和短提示auxj.局部验证过程如下:

2) 计算ZAj=H256(ENTLAj‖IDAj‖a‖b‖xG‖yG‖xAj‖yAj);

5) 计算d=(auxj1+ej) modn;

6) 计算h1=Hv(auxj1);

7) 计算xj=(auxj2-h1) modn;

8) 计算yj=(auxj3-h1) modn;

9) 计算(x,y)=(xj,yj)+UG+tjPAj;

10) 计算R′=(d+x) modn.

检查等式R′=R是否成立,若成立则验证通过,否则验证不通过.

3 方案分析

3.1 正确性分析

令E=Hv(e1‖e2‖…‖eL),则相同签名者时的聚合验证公式为

(1)

则只需验证

(2)

其证明过程如式(3)所示.不同签名者时及局部验证时的证明过程与相同签名者时相似,不再赘述.

(3)

3.2 安全性分析

SM2-LAVS方案单个SM2签名步骤,相较于标准SM2算法签名流程,对于明文Mi,生成签名由(ri,si)变为(ri,si,vi),其中vi=(ei+yi).如果敌手得到明文Mi哈希值ei,则可计算出yi,而在SM2算法标准验签流程中,检验

R′=(ei+xi)=ri,

(4)

其中xi通过(xi,yi)=siG+tiPA计算得到.由此可知,敌手可通过一定的计算得到签名时的xi,yi,因此,在单个SM2签名步骤中新增vi字段并不会使本文方案安全性低于SM2标准算法.

在聚合验证步骤时,需要验证

(5)

(6)

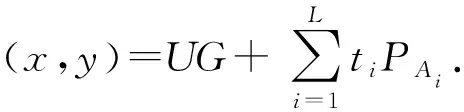
在局部验证步骤时,需要验证

R′=R,

(7)

auxj1+ej+x=R.

(8)

4 方案实现与性能分析

本文使用C++语言实现SM2-LAVS方案并调用GmSSL库实现SM2中椭圆曲线上计算.实际开发环境中CPU为Intel i5-9400,内存为8GB,操作系统为Ubuntu 18.04.

表1定义了密码运算的符号,并通过重复运行1000次运算取其平均值的方法得出单次运算所消耗时间.

表1 单次密码运算所消耗时间 ms

表2分析了在相同签名者和不同签名者2种情况下各个步骤计算成本对比.

表3对比了几种聚合签名方案及本文方案的计算成本.

图1所示为不同聚合签名方案聚合验证时间开销对比.

由图1可知,随着明文消息数量增大,本文方案聚合验证开销在几个方案中最小,因此,本文方案与同类方案相比,具有较高性能.

表2 各个步骤计算成本对比

表3 各个聚合签名方案计算成本对比

图1 不同聚合签名方案时间开销对比

5 结 语

本文基于国密SM2算法设计一种局部可验证聚合签名方案,利用聚合签名提高验证方验证效率,通过局部可验证使验证方对聚合签名及指定明文验证时,无需获取全部明文.通过与现有若干个聚合签名方案对比,证明本文方案聚合验证开销更低,具有一定优势.但本文方案聚合签名长度与签名者数量呈线性相关,将来可以进一步优化,将签名长度优化为常量值,降低通信开销.