基于时间卷积模型的GNSS多路径误差削弱

李思辉,刘 超 ,张开坤,王向阳,段 伟,孙景强

(1.安徽理工大学空间信息与测绘工程学院,232001,安徽,淮南;2.南京市测绘勘察研究院股份有限公司,210019,南京;3.徐州矿务集团有限公司资产开发管理部,221140,江苏,徐州)

0 引言

全球导航卫星系统(Global Navigation Satellite System,GNSS)因其全天候、高精度和实时化等优点在地震形变、水汽反演和滑坡监测等众多领域中得到应用[1-3]。但在进行定位的过程会受到诸多因素的影响,主要包括接收机钟差、卫星钟差、对流层和电离层延迟误差、多路径误差和随机误差等。短基线相对定位是定位的主要方式,其通过差分的方式可以消除卫星钟差和接收机钟差,也可以基本消除对流层和电离层误差,但是多路径误差无法通过差分的方式消除,所以在短基线相对定位中多路径误差成为影响GNSS高精度定位主要的因素。

削弱多路径误差的方式主要分为三个方面:选取合适的地址、硬件以及数据处理方面。合适的选址是一种简单有效的多路径误差抑制方法,站点应尽量选择在开阔和无明显反射源等环境。硬件方面主要是改进接收机硬件,比如加装抑径板、改进扼流圈[4]等。数据处理方面主要有基于时间域的恒星日滤波(Sidereal Filtering,SF)、基于空间域的多路径半天球模型(Multipath Hemis pherical Map, MHM)以及基于高度角和信噪比等随机模型[5- 6]来抑制多路径误差。

当测站位置固定且周围环境相同时,多路径误差会随着卫星位置周期性移动而呈现出周期性变化,Genrich等[7]根据这一特性首先提出恒星日滤波方法(SF),由于卫星的重复周期并不是恒定的,Choi等[8]使用平均轨道重复周期用于恒星日滤波中。为顾及卫星间的差异,恒星日滤波发展到了观测值域[9-10]。无论是坐标域还是观测值域的恒星日滤波,精确计算卫星的重复周期是该方法的关键,而在GNSS中不同的系统有着不同的卫星星座,并且同一颗卫星的重复周期并不完全一致,这就给精确估计周期增加了复杂性,同时坐标域恒星日滤波方法难以应用于GNSS多路径削弱中。Dong等[11]依据静态环境下多路径效应时空可重复的特性,根据卫星的高度角和方位角建立多路径半天球模型(MHM)。Wang等[12]提出基于趋势面分析多路径半天球模型用于缓解高频和低频多路径。王亚伟等[13]根据双差观测值残差构建网格点参数建立半天球网点模型。尽管MHM可以较好地适用于GNSS中,但是为顾及多个系统建立多路径模型需要数天的数据,在GNSS中可见卫星数据巨大,使得计算效率比较低下。

而近年来深度学习飞速发展,因其能够深度挖掘数据的特征和具备强大处理复杂非线性问题的能力,在GNSS领域有着广泛应用。考虑到经典恒星日滤波难以适用于GNSS多路径削弱中以及半天球模型需要大量数据支持计算效率低下的问题,本文引入了深度学习中的时间卷积网络(Time Convolutional Network, TCN)模型,深度挖掘GNSS数据之间的特征,学习数据深层次的规律,对短基线相对定位中的多路径误差进行改正。

1 相关原理

1.1 多路径误差原理

在GNSS定位过程中,接收机接受到的卫星信号并不完全是由卫星直射信号构成,其他的信号有来自测站周围环境的反射信号或衍射信号,这些信号与卫星直射信号产生干涉,使得观测值偏离真值,这种现象成为多路径效应。多路径效应的强弱与周围环境的复杂程度有关,周围环境反射物较多或者是反射物体反射率越大时,多路径效应越明显。定位过程中往往是由多个反射信号与直射信号相干涉,由多个反射信号造成的多路径误差可表示为:

(1)

式中,φm为多路径误差造成的相位延迟,αi为第i个反射信号反射系数,φi为第i个反射信号的相位延迟。

1.2 TCN模型原理

TCN网络[14]是一种特殊的卷积网络,适用于处理时间序列问题。不同于RNN,TCN不必按时间前后顺序处理时间预测问题,而是可作为一个整体来处理,同时TCN网络中可以灵活地改变感受野的大小,以获取更长时间序列之间的关系。TCN的网络架构主要有三部分构成:因果卷积(Causal Convolution)、膨胀卷积(Dilated Convolution)和残差连接。

1.2.1 因果卷积 因果卷积即指在处理时间序列问题中,按照时间的先后顺序,当前时刻的输出只会受到当前时刻以及以前时刻的输入影响,而不受未来时刻的影响。如图1所示,t时刻的输出只与t时刻和t时刻之前的输入有联系,使得信息不会泄露,并且为了保证输出的时间序列长度与输入的时间序列的长度保持一致,在因果卷积中进行了单边零填充的操作。但是对于长时间序列,输出结果要想获得充足历史信息增大感受野,就需要堆叠很多网络层数,也就容易造成了梯度爆炸和计算量增加的问题,为了解决这个问题,TCN网络模型中引入了膨胀卷积。

图1 因果卷积示意图

1.2.2 膨胀卷积 膨胀卷积也称空洞卷积,与普通卷积不同,膨胀卷积包含一个扩张系数,用以增加感受野。对于时间序列x∈Rn的元素s,则膨胀卷积计算公式为:

(2)

式中,f(i)为权重参数,d为膨胀系数,xs-d·i为当前时刻之前的数据。TCN模型可以使用更大的膨胀系数获得更长的序列依赖关系,使得整个网络模型的感受野得到扩展。

图2展示的是滤波器为2,膨胀系数为1、2、4的膨胀卷积结构示意图,可看出在TCN模型中可通过设置d的大小控制模型中的感受野的大小,同时TCN网络模型的感受野会随着膨胀系数的增大呈指数型的增长。为了提升网络的稳定性,避免网络退化问题,TCN引入了残差连接。

图2 膨胀卷积示意图

1.2.3 残差连接 扩大感受野还可以通过增加隐藏层数量的方式,但过深层的网络会造成整个网络的不稳定,出现梯度消失和计算效率下降问题。TCN模型中残差连接能有效解决深层网络的性能下降问题,使得网络模型更加稳定,残差连接包括两层膨胀因果卷积和非线性映射函数。

1.3 基于TCN的GNSS多路径误差实时削弱流程

TCN模型架构如图3所示,在TCN模型削弱多路径误差中,坐标序列按照一定的步长输入到TCN网络当中,通过网络模型中的膨胀因果卷积提取数据之间的特征信息,并且通过使用残差连接来提高整个网络的稳定性,具体步骤为:

1)通过反复调节确定合适的超参数构建TCN网络;

2)选取某天坐标序列作为训练样本,进行网络迭代训练;

3)训练结束后进行实时预测;

4)将坐标序列与预测出来的多路径误差进行改正。

2 实验结果与分析

2.1 数据获取

本节实验数据采集于安徽理工大学某学院楼楼顶GNSS连续跟踪站,基准站和流动站均在同一楼顶,两测站点基线长度12.92 m, 使用2台相同类型接收机采集数据,接收机类型为中海达iRTK10接收机,采样频率为1 Hz,卫星高度截止角为15°。数据选取基准站和流动站2022年DOY120至DOY134(共15 d观测数据)观测数据。数据经过差分处理后,钟差、电离层和对流层等误差基本上可以消除,因此可认为坐标残差序列中只存在多路径误差和随机噪声。

2.2 实验结果及分析

为验证TCN模型在多路径抑制方面的效果,以DOY120的观测数据作为模型训练数据,对后面14 d的观测数据进行预测,并进行多路径误差改正,但限于篇幅仅以DOY121的坐标序列为例。由于坐标残差基本是由多路径误差和噪声构成,改正后残差的波动情况可看出模型对多路径误差改正的效果。以E方向为例,对改正前后坐标残差序列进行傅里叶变换分析,如图4所示,改正后的坐标残差序列频率在0.02 Hz以下部分明显降低。以前的研究表明,多路径表现为低频特性,TCN模型可有效削弱多路径。如图5所示,模型预测出来的坐标序列和原始的坐标序列的趋势基本一致。使用预测出来的坐标序列改正原始坐标序列,得到的残差序列基本在零附近波动,如图6所示。统计结果表明,本文所使用的TCN模型用于多路径误差的抑制是可行的,且改正后效果较为明显。

图4 DOY121各方向功率谱密度图

图5 原始坐标序列和预测坐标序列

图6 改正后坐标残差

为了验证模型的泛化性,使用DOY120的数据训练出来的模型对后续14 d的数据进行多路径误差改正,并计算改正后的RMS值,统计结果如表1所示。从表1中可以看出,DOY121到DOY134的E、N、U方向原始数据RMS值的平均值分别为1.50、1.99、3.48 mm,经过改正后的各方向上的RMS值分别为0.86、0.90、0.40 mm,平均改善程度分别为41.95%、54.27%、40.05%,DOY121-DOY134每天各方向上的改善程度会波动,但波动程度较小,整体较为平稳,说明TCN模型对多路径误差抑制有良好的泛化能力。

表1 DOY121-DOY134各天坐标序列改正结果均方根/mm和改善程度/%

为了进一步验证TCN网络对多路径抑制的效果,本文使用MHM方法与之对比,使用DOY120-DOY126(共7 d)的数据建立MHM模型,并对后8 d进行改正。首先提取出各天各个卫星对应的双差残差值,采用“零均值”转为单差残差,采用1°×1°的网格,把对应的高度角和方位角匹配在网格中,最后计算平均值得到每个网格中的多路径值,以此建立起MHM模型。如图7所示,经过MHM模型对坐标序列改正后RMS值与原始RMS值相比改善明显。而经过TCN模型改善多路径后的坐标残差RMS值明显低于MHM方法改善后的结果,且保持平稳的趋势。在E和N方向上,随着时间的增加,MHM方法的改善程度有所下降,而TCN模型的改善程度相较于MHM方法改善程度来说较平稳。MHM方法对E、N、U方向坐标序列的改善程度平均为17.98%、42.09%和24.61%,而TCN方法改善程度平均为38.72%、54.76%和39.52%,见表2。TCN模型对各方向上坐标序列的改正结果均优于MHM方法。

表2 MHM和TCN方法平均改正均方根/mm和改善程度/%

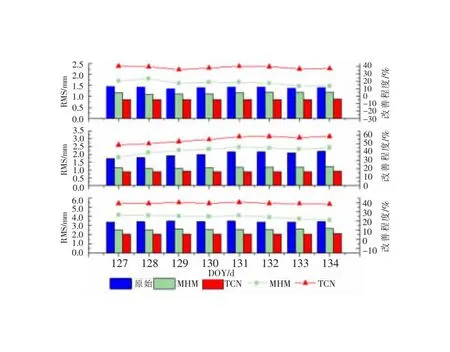
图7 DOY127-DOY134各天MHM和TCN改正结果

3 结束语

考虑到坐标域SF方法难以适用于GNSS中以及MHM方法建立多路径模型需要数天的数据,鉴于深度学习具有良好处理复杂非线性数据和挖掘数据间特征的能力,本文引入了TCN网络模型抑制多路径误差。通过实验分析,得出如下结论。

1)经TCN模型改正后,坐标残差序列的低频部分明显降低,验证了该网络模型在抑制多路径误差的可行性。

2)改正后的E、N、U方向坐标序列残差精度明显提高,平均改善分别为41.95%、54.27%、40.05%。

3)TCN方法抑制多路径的效果要优于MHM方法,并且随着时间增加TCN改善效果的稳定性要优于MHM方法,表明TCN模型具有良好的泛化能力。