列车制动盘散热特性分析及拓扑优化
2024-03-04卢耀辉史潇博唐波李腾宇
卢耀辉,史潇博,唐波,李腾宇
(西南交通大学 机械工程学院,四川 成都 610031)
近年来,我国铁道技术发展迅猛,整个铁路网已成为全世界最先进、发展速度最快的铁路系统。列车行驶速度的不断提高,使得人们对其安全性的要求也越来越高,制动安全作为一项重要安全指标,引起了广泛重视。
制动盘的工作原理大都是将其与设备中起驱动作用的回转轴相连,通过夹钳与其接触、摩擦,使转动降速乃至停止。在制动过程中,设备的动能转化为热能,其中一部分转化为摩擦物体的内能,另一部分耗散至环境[1]。摩擦热产生的热斑、热裂纹等损伤将影响制动盘摩擦学性能,并降低其服役寿命。Hong等[2]通过建立热-力耦合模型分析了韩国KTX高速列车(300 km/h)制动盘的热疲劳问题,最终仿真结果与试验结果趋势一致。杨源等[3]引入尺寸因子的概念以表征制动盘面温度分布,发现尺寸因子值与盘面温度场成正比关系,减小制动盘尺寸因子可以降低盘面温度梯度。周素霞等[4]对热应力作用下制动盘应力场进行了计算,得到了其裂纹扩展寿命,为制动盘后续研究提供了参考。在制动盘散热结构研究方面,王玉光等[5]采用CFD分析制动时制动盘的温度场变化以及二次制动的温度场,得到的换热系数的分布规律与试验结果基本吻合,证明了CFD可以用于分析高速列车制动过程。Yan等[6]通过对制动盘摩擦面进行开孔来研究其换热的影响,发现开孔后虽然可以提高整体换热能力,但由于钻口处气流与主流的相互作用,会造成局部传热恶化。Chopade等[7]通过试验与模拟对比分析了制动盘不同形式散热筋的换热情况,发现变径型圆柱散热筋拥有更好的散热率。随着计算能力的提升,通过热流体拓扑优化来实现精确的解决方案引起了更多重视。其中,Gil等[8]最开始对强制对流进行了研究,后续许多学者在此基础上进行了扩展。Dilgen等[9]提出了湍流流场和强制换热场的拓扑优化方法。Haertel等[10]与Zeng等[11]提出了一个连接固体热基层和流固层的伪三维热流体模型。Dilgen等[12]实现了湍流强制对流换热散热器的拓扑优化,证明对于多物理场复杂的优化问题,之前的湍流拓扑优化方法具有可拓展性。
本文为改善制动盘散热问题,使用拓扑优化方法,分析散热筋结构对列车制动盘周围流场的影响,并对换热系数的变化规律进行分析,以寻求一种新型的散热结构,实现制动盘散热能力的提高。
1 通风式制动盘散热特性仿真计算
1.1 计算模型及边界条件
本文以某型号列车制动盘为例,分析以200 km/h速度制动时,制动盘与空气的对流换热情况。制动盘内圈直径为350 mm,外圈直径为640 mm,由于是中心对称,取模型的1/9进行分析,见图1。计算边界条件见图2及表1。
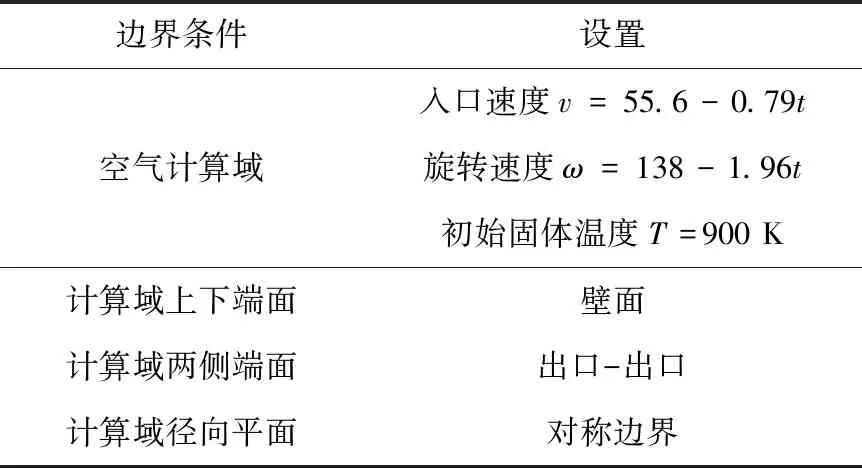
表1 边界条件设置

图1 制动盘整体模型

图2 计算边界条件示意图
制动盘在实际服役过程中,运动状态包含直线与圆周旋转。本文通过设置入口速度,模拟制动盘随列车进行的直线运动;通过MRF参考系建立旋转模型,使制动盘与流体域之间产生相对圆周运动。使用Fluent Meshing软件划分六面体-多面体网格,并对流固交界面设置加密层,加密层为5层,增长率为1.2,划分好的网格见图3。根据制动盘实际的服役工况设置边界条件,采用计算流体力学分析软件Fluent对制动盘进行流场瞬态分析,其边界条件设置为:

图3 计算域网格示意图
(1)计算域中制动盘内径方向边界设置为流场入口,外径方向边界设置为流场出口。
(2)制动盘固体域的温度设置为900 K,流体域温度设置为300 K。
(3)制动盘做匀减速运动,制动初速度为200 km/h,制动时间70 s。
(4)采用二阶迎风格式,残差收敛度为0.000 1,不考虑重力影响。
1.2 计算方法验证
为验证所使用的模拟方法的准确性,本文将国内外制动盘散热试验进行对照,由于通过试验测量列车对流换热系数较为困难,故参考Wallis等[13]对汽车通风制动盘的研究。采用本文的模拟方法建立的制动盘模型见图4。其制动盘外圈直径为290 mm, 内圈直径为180 mm。SRV型制动盘通风通道出口处筋板为直角,SRVR型制动盘其通风入口处圆角筋板为半径2.5 mm圆角,计算域设置与上文一致。

图4 汽车制动盘结构
将模拟结果与文献进行对照,以验证模拟的准确性,结果见图5。曲线LW-SRV和LW-SRVR为参考文献数据,S-SRV和S-SRVR为模拟得到的数据。模拟得到的数据要略微低于文献中的数据,但误差较小,且变化趋势一致,故认为本文所采用的模拟方法基本可行。

图5 数值模拟与文献对比结果
2 制动盘流场及对流换热结果分析
2.1 制动盘流场分析
图6为制动过程中制动初期(0 s)与后期(60 s)时空气流经制动盘叶片筋通道时的速度场横截面分布云图。可以看出,速度场从散热筋的迎风面到背风面有着明显的分层现象,在靠近背风面的区域,速度分布更加均匀,但整体数值偏低;迎风面处速度场受气流冲击影响,更加紊乱,同时流场速度更大,有利于对流换热。

图6 制动盘内部速度场分布云图
比较制动初期与制动后期速度场,除整体速度场随运行工况同步降低外,分布规律基本一致。但通过对比迎风面附近速度分布情况可以看出,制动盘后期速度场分布更加均匀。
2.2 对流换热结果分析
表2为不同制动时刻的制动盘对流换热系数分布。可知,对流换热系数随制动时间呈现下降趋势,在制动后期,对流换热系数下降更快。

表2 不同制动时刻制动盘对流换热系数分布
图7为制动初期(0 s)与后期(60 s)制动盘散热筋板对流换热系数分布云图。可知,筋板对流换热系数与速度呈现极大相关性,即速度相对较大的迎风面上,对流换热系数也更大,而在速度场较小的背风面,对流换热系数显著低于迎风面处。与图6结合可知,随着制动的进行,制动盘周围速度场降低,流场从强烈湍流状态逐渐缓和,导致换热效果下降更快;同时靠近制动盘外径处的散热筋换热效果要显著高于内径处的散热筋。其原因是制动盘内部换热通道中散热筋空间分布较为均匀,故在径向入口方向的直线气流速度不会造成过多的损耗,同时由于更靠近旋转外侧,其外径附近轴向速度更大,故外径处散热筋换热效果优于内径处。
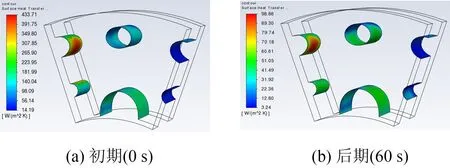
图7 对流换热系数分布云图
3 优化设计
3.1 优化问题描述
本文基于密度法对通风式制动盘散热筋结构进行拓扑优化。图8为制动盘优化模型示意图,本文为简化计算,将制动盘散热模型降维至二维模型。二维模型边界条件参考上文三维模型进行设置,优化目标为固体域温度最小。同时为保障制动盘筋面的基本形状,对模型进行体积约束。图8中阴影部分为优化区域,内环为散热筋自身区域,外环为允许散热筋向外延伸区域。

图8 制动盘优化模型示意图
3.2 控制方程
通过模拟孔隙渗透率与材料建立拓扑关系,确定通道内多孔材料的最优分布,达到平均温度最小。本文引入Brinkman摩擦项,假定流体阻力F与流速u成正比,即F=-αu,其中α为渗透率。根据有限元的思想将设计域离散化,设计变量取0~1间的任意值。
在拓扑优化过程中,固体域和流体域的区分将根据每次迭代结果的不断变化,所以引入设计变量γ来对渗透率与材料属性进行插值。下面对模型热力学属性中的比热容cP、热传导系数k进行插值,插值后的函数为:
α=αmax+(αmin-αmax)p(1-γ)/(p+γ)
(1)
CP=CPs+γ(CPf-CPs)
(2)
k=ks+γ(kf-ks)
(3)
式中:CPf、CPs为流体和固体材料比热容;kf、ks为流体和固体材料的导热系数;γ为设计变量。在流体拓扑优化问题中,αmax的值越大表示阻尼越大,渗透率越接近理想情况。在本次研究中取αmax为1×105,αmin为0,p为惩罚因子,用来确定插值函数模型的惩罚效果,p值越小,最终的插值会越向两端逼近,材料单元可以实现无限逼近流体或固体,减少中间灰度密度单元,本文中p取值为0.001。γ=0,α=αmin,表示设计区域为固体域;γ=1,α=αmax,表示设计区域为流体域。
结合N-S方程后的优化列式为:
(4)
式中:Ω为设计域;f为体积分数。
3.3 优化结果分析
拓扑优化迭代过程中材料体积因子变化见图9。可以看出迭代过程中灰度区逐渐消失,这意味着优化结果朝着收敛方向发展,最终形成密度值0~1的分布,所优化的孔隙度域展示了清晰的拓扑结构,可以作为当前制动盘散热筋结构优化的参考。本文通过Ansys Scdm对二维平面纵向拉伸,形成新的散热结构,见图10。

图9 拓扑优化迭代结果

图10 优化后模型示意图
图11为制动盘优化后散热筋对流换热系数云图。与优化前对比,整体数值有所上升,但也存在着局部散热系数降低的情况, 为了更加直观地评价制动盘散热能力,本文以制动盘整体热流量与平均对流换热系数作为散热能力的最终评判标准。图12为制动盘运行时间与散热能力的变化曲线。由图可知,制动盘散热能力与运行速度呈非线性正相关关系, 且优化后其散热能力在运行工况的各时间段均有所提升。随运行时间增加,制动盘周围流场逐渐稳定,优化后的筋板对气流的扰动减弱,性能提升量降低。同时随运行时间的增加,对流换热降低的同时,由于高换热系数处温度降低较快,导致温差降低,这是优化后模型散热量降低较快的另一大因素。优化后模型与原制动盘模型相比,整体散热量提升了13.46%。

图11 优化后模型对流换热系数分布云图

(a) 制动盘平均对流换热系数
从优化后的温度云图(图13(b))可以看出,在对筋板结构进行了优化后,气流受筋板过渡角的影响,提高了通风道的气流湍流度,增强了制动盘散热。对于优化后的制动盘,由于增大了对气流的扰动作用,加快了热流交换速率,提高了制动盘散热特性。制动末期(t=70 s)散热筋温度分布与对流换热分布图基本对应,制动盘的温度场存在明显的梯度变化,温度从迎风面向背风面有显著的增长趋势,最大温度集中在背风面筋板附近。优化后的模型相对低温区域明显增加,迎风面高温区由背风面向中部延伸的趋势也有所减弱。因此,基于拓扑优化方法的制动盘散热优化具有一定可行性。
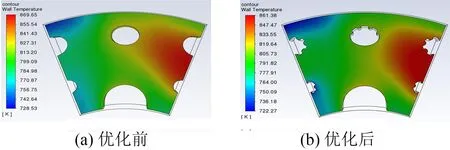
图13 制动盘内表面优化前后温度分布云图
4 结论
(1)列车制动盘筋板结构对制动盘换热影响较大,而对于圆柱型筋板,其流场结构受扰流影响较为复杂,使用传统优化时难以确定优化方向。
(2)制动盘散热筋对流换热系数受其位置影响较大,由于受绕流效果的影响,制动盘筋板旋转背风面换热效果较好。同时,在径向方向靠近制动盘外径处,由于受周围通风道气流流速较大,有助于对流换热,因此径向通风道外缘处散热筋的对流换热系数较散热筋更高。
(3)通过对制动盘散热结构进行拓扑优化,将整个制动工况的整体散热量提升了13.46%,验证了拓扑优化在制动盘散热方面的积极作用。
(4)本文优化过程中将一些条件进行了简化,可能会对结果产生一定的影响,后续考虑采用三维优化模型对其进行优化计算。
