基于模态分析的宽频带振荡区域定位研究

周生奇，菅学辉，钟世民，孙鹏菊，李 强

（1.国网山东省电力公司青岛供电公司，山东 青岛 266002；2.重庆大学，重庆 400044）

0 引言

近年来，我国能源战略转型向纵深推进，可再生能源正逐步取代传统化石能源。风电、光伏等新能源装机容量不断增加［1-2］。电力系统“双高”特性日益显著，系统安全可靠运行面临更为复杂的挑战。由于新能源发电涉及大量电能变换装置，其中电力电子装置引发的宽频带振荡对系统稳定性产生较大的影响，使其备受关注［3］。

国内外此类系统运行事故时有报道［4-7］，例如2015 年7 月，哈密地区风电场出现的次同步振荡甚至导致火电机组跳闸，影响巨大。广西永福串补输电系统发生3Hz 附近振荡，河北沽源风电串补系统发生3～12Hz 振荡，上海南汇风电柔直系统发生20～30 Hz 振荡，德国北海风电柔直系统发生250～350 Hz振荡，浙江舟山柔直系统发生1 000 Hz 附近振荡，塞罕坝风电系统发生1 050 Hz 附近振荡，青海光伏发生1 350 Hz 振荡。上述事故的发生与新能源发电密切相关，随着清洁能源上网电量不断增加，新能源系统出力的间歇性、随机性以及系统阻抗的波动性，导致系统稳定性面临严峻的考验。所以宽频带振荡研究对建设以新能源为主体的新型电力系统具有重要的意义。

目前针对多逆变器系统的相关研究，主要集中于同类型等效合并分析、系统各部分电流判稳、逆变器与电网的耦合效应分析等方面。文献［8-9］针对多逆变器并联谐振问题，将系统中的逆变器作为激励源，按类别进行分类合并，降低分析复杂度。载波同步时，系统稳定；反之，系统谐振。但是该方法忽略同类激励源之间的相互影响。文献［10］推导大型光伏电站系统的闭环特征方程，利用根轨迹对电网阻抗波动的情况进行新能源系统稳定性分析。根据系统闭环极点随并联台数变化的运动轨迹，确定系统稳定运行时并联逆变器台数的上限，确定系统安全运行范围，为系统最大限度安全运行提供参考。但是该方法在逆变器数量较多，且种类较多时，闭环极点的计算量大，影响该方法在实际生产应用中的效果。文献［11-12］为了简化多逆变器系统的分析，根据逆变器输出电流的流动方向进行输出电流分离。当各部分电流都不发生谐振且稳定，则系统稳定。但是该方法对不同型号逆变器并联系统分析难度大。文献［13］认为新能源系统发生谐振的根源在于公共耦合点（point of common coupling，PCC）两侧阻抗发生耦合，若逆变器的输出阻抗存在负阻尼，当PCC 点两侧的逆变器输出阻抗和电网阻抗幅频交点处于该频段时，系统发生谐振失稳。文献［14-15］建立了多并网逆变器系统模型，分析系统谐振特性的受影响因素，明确系统各类型参数变化对多逆变器系统谐振特性的影响规律。多台逆变器并联系统具有多个谐振频率，逆变器的数量、类型和组成比例都会对谐振频率造成影响。文献［16-18］利用模态分析方法研究滤波器、电网阻抗等系统参数对谐振频率的影响趋势，但是文献只是分析了谐振峰受影响的变化趋势，并没有对现象的成因及相关应用进行更加深入分析。

在文献［19］中，以风电场为例，讨论由逆变器引起的有源阻抗和无源阻抗之间的相互作用。这种阻抗之间的相互作用也发生在光伏发电场中，如文献［20］讨论了并联运行时，电网阻抗值对逆变器电流质量的敏感性问题。文献［21］中的分析具有系统精确描述的优点，但当逆变器不相同且缺乏模块化时，因为不同逆变器的加入需要重新进行系统描述，所以变得难以应用。另一方面，基于阻抗的方法可以克服这些缺点，但并没有给出相应的稳定性贡献，特别是内部不稳定状态下，系统各部分对于不稳定的贡献度。

因此，针对不同型号逆变器并联系统的宽频带振荡问题，分析其振荡的产生机理，提出一种基于模态分析的宽频带振荡区域定位方法。根据逆变器参数、线路阻抗参数和电网阻抗参数，建立系统高阶导纳矩阵，获取模态阻抗随频率的变化曲线，提出节点参与因子来定位振荡区域。

1 多逆变器系统并网模型

LCL 型滤波器相比于L 型滤波器，具有良好的高频谐波衰减能力，且LCL 型滤波器中两个电感的电感量之和小于L 型滤波器的单个电感的电感量，因此体积更小，成本更低。所以并网逆变器通常采用LCL 型滤波器，以保持良好的高频谐波衰减能力，减小开关频率谐波对系统的影响［22］。单相逆变器的控制结构如图1 所示。电流环控制器为比例谐振（proportion resonance，PR）控制器，Gi（s）为电流控制器的传递函数。H1为电容电流反馈系数，采用电容电流有源阻尼的方式，其实相当于在滤波器电容上并联电阻；H2为并网电流反馈系数，其大小由并网电流指令值和系统的功率等级确定；i2*为并网电流指令，由电网相角与并网电流给定相乘获得；vM为控制器输出的调制信号；SPWM 为正弦脉宽调制（sinusoidal pulse width modulation，SPWM），PLL 为锁相环（phase-locked loop，PLL），L1、L2和C分别为滤波器的逆变器侧滤波电感、网侧滤波电感、滤波电容。

图1 单台逆变器并网控制结构图Fig.1 Control structure diagram of single inverter

逆变器并网控制如图2 所示。i2*（s）为电流参考信号；Gd（s）为数字控制延时环节，主要包含计算延时和采样延时两个部分，Gd（s）=e-1.5sTs，Ts为采样周期；Kpwm为逆变器等效环节，取值为直流侧电压与三角载波幅值之比。

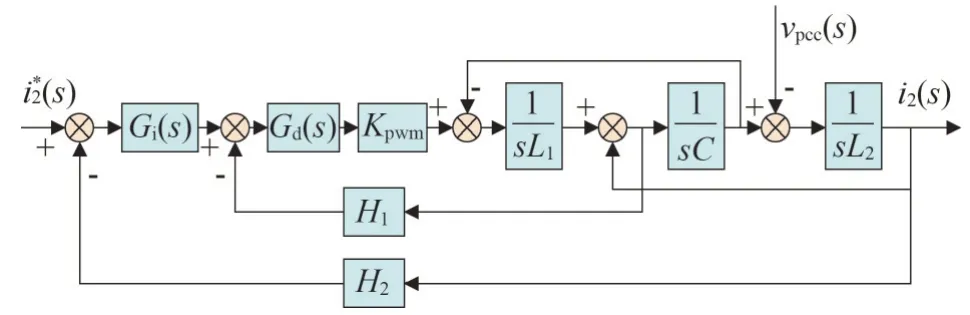
图2 逆变器并网控制框图Fig.2 Control block diagram of inverter

考虑电网阻抗和线路阻抗，结合图2，可以得到逆变器并网系统诺顿等效模型，如图3 所示。Yo（s）为逆变器输出导纳，如式（1）所示。Yf（s）为线路导纳，Yg（s）为电网阻抗，vg为理想电压源，Go（s）为电流参考信号i2*（s）到等效电流源的传递函数。

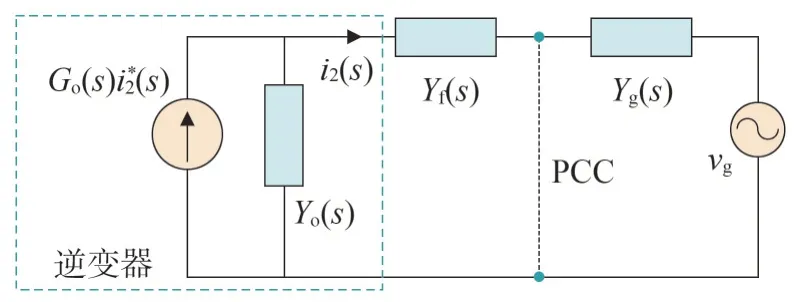
图3 逆变器诺顿等效模型Fig.3 Norton equivalent model of inverter

根据图3 的逆变器诺顿等效模型，可以得到单相逆变器的并网电流表达式，如式（2）所示。在理想电网条件下，即电网阻抗为零，按照设计要求，此时系统应稳定，所以式（2）的（is（s）-vg（s）/Zo（s））部分稳定。对于单台逆变器系统而言，其运行稳定性由（Zg（s）+Zf（s））/Zo（s）决定［23］。

由于多逆变器并联运行时，一般在PCC 点并联，并与电网阻抗串联。所以根据单台逆变器的诺顿等效模型，多逆变器系统PCC 点并网的模型如图4所示。

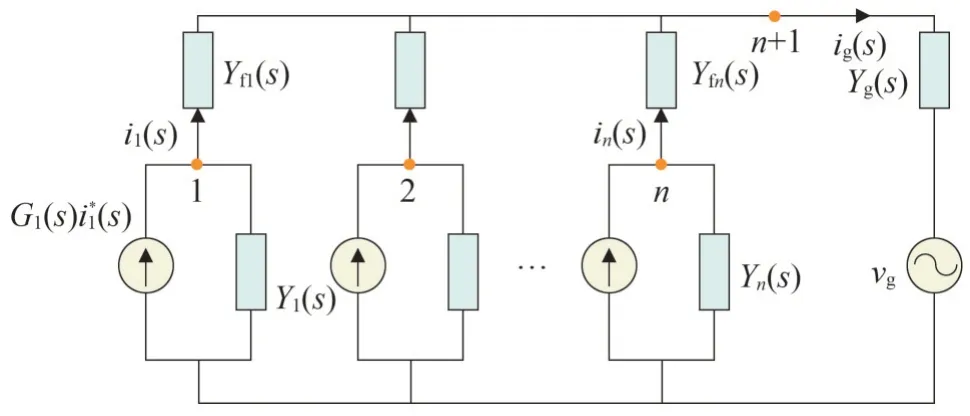
图4 多逆变器系统并网等效模型Fig.4 Equivalent modeling of multi-inverter systems

2 宽频带振荡区域定位

模态分析是结构学中研究固定激励下系统特定震动模态的方法，后将其引入电力系统的谐振分析。假设某一系统发生谐振，将某一频率的谐振定义为谐振模态，即认为系统出现过电压或者过电流现象，所以对此时的系统特性进行分析为

式中：U为谐振电压矩阵；Y为导纳矩阵；I为谐振电流矩阵。

假设在正常电流激励条件下，电压出现较大值，则是由于导纳矩阵Y出现了极小值。对其进行求倒数后，导纳矩阵出现极大值，故对导纳矩阵进行特征值分解，可得

式中：L为左特征向量；T为右特征向量；Λ为对角矩阵。

对左特征向量L、右特征向量T进行移动，与电压、电流进行重新组合，定义新的系统参数模态电压V=TU，模态电流J=TI，此时就可以将导纳矩阵化简成对角矩阵，实现系统解耦，并形成模态导纳λ。

对于模态电流J1，通过提取表达式可以进一步分析其特性为

可知右特征向量T与电流相乘，即为电流的系数，表征谐振模态的可激励性。同样，模态电压进一步推导，假设模态*发生谐振，则有

由于发生谐振，认为V*远大于其他值，所以进行如式（7）的近似。左特征向量L表示谐振电压U的可观测性。对于一个固定系统，λ值随频率变化。当λ出现极小值λm，则倒数出现极大值，即模态阻抗出现极大值，此时在正常电流激励下，电压也会出现较大值，判定系统发生谐振，也称关键模态m。此时表达式如式（8）所示。

其对角元素体现了同一节点在关键模式下可激励性和可观测性的结合，故称其为关键模态的参与因子（participation factor，PF），表示为F，如式（9）所示。

式中：b为系统母线号；m为谐振模态号，可反映系统各节点在谐振情况下的表现。

根据不同的逆变器群结构类型，结合完整的系统参数，即可建立相应的系统等效模型及其对应的导纳矩阵。在某一频率范围内进行特征值分解，得到随频率变化的模态阻抗曲线和关键谐振模态，再对左特征向量和右特征向量进行合并，即可得到参与因子。根据参与因子的表现，可以确定系统谐振发生时各节点的状态，即确定各台逆变器的谐振表现，并结合系统谐振类型的划分，从而实现振荡区域定位。针对多逆变器系统的谐振模态分析流程如图5 所示。相关算法主要借助MATLAB 实现，建立系统模型，利用定步长和循环语句，进行对角矩阵的运算，并借助图形可视化输出相应的计算结果。

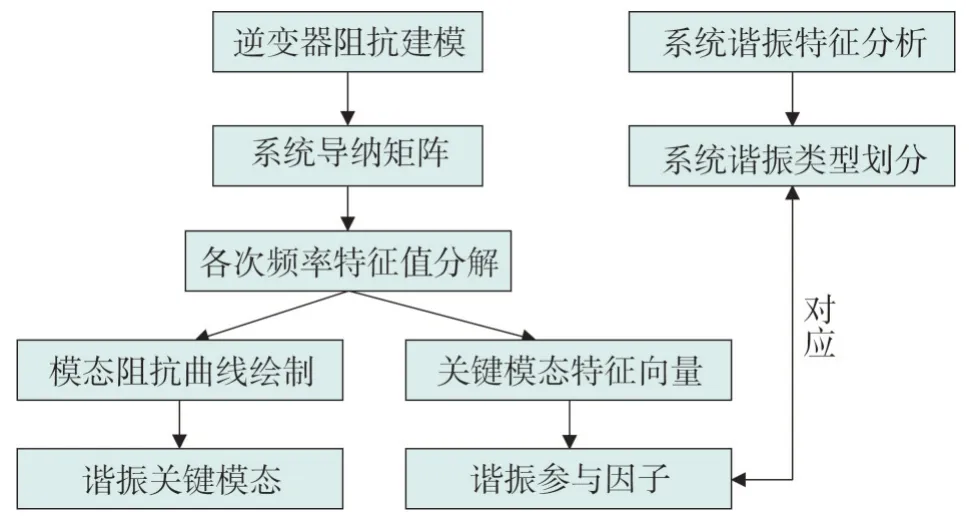
图5 谐振模态分析流程示意图Fig.5 Flow chart of resonance modal analysis

3 算例分析

以两台不同型号1.5 MW 逆变器并联的系统为例（组合1∶1），开关频率为2 kHz，采样频率为20 kHz，参数如表1 所示，两种逆变器型号的差异主要是滤波器参数、控制参数存在差异。根据图5 模态分析方法的流程图，建立多逆变器系统的导纳矩阵，分别进行各次频率下的矩阵特征值分解，绘制模态阻抗随频率变化的曲线；进行参与因子计算，获取各节点的参与因子，相应的模态分析结果如图6 和表2 所示。其中，电网阻抗根据短路比SCR=3 计算所得［24］，线路阻抗采用文献［16］参数。

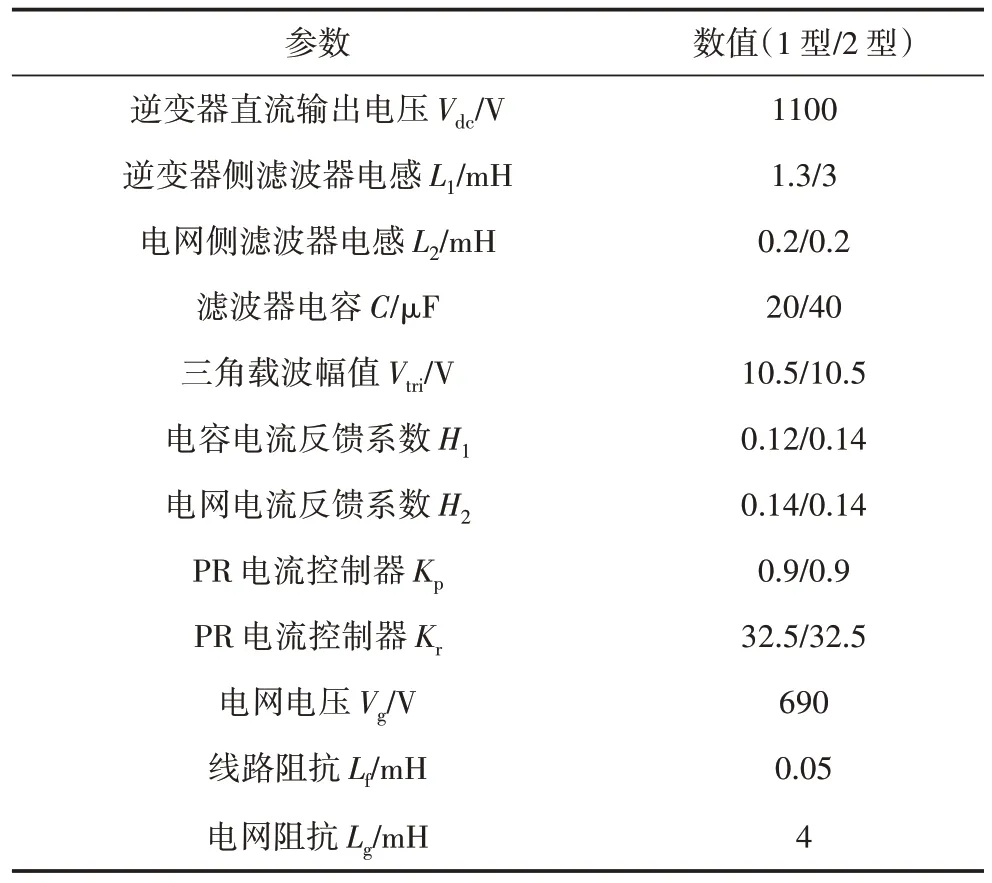
表1 系统仿真参数Table 1 Simulation parameters of system

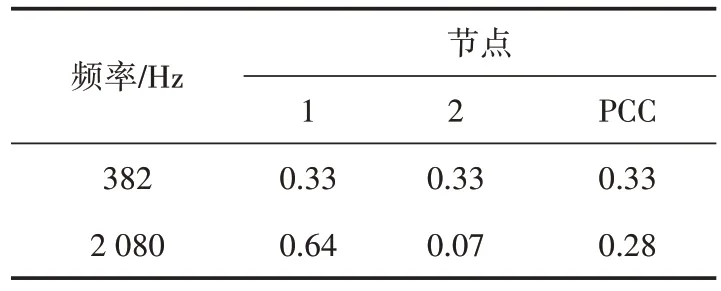
表2 关键模态下节点参与因子Table 2 Nodal participation factor of critical modes

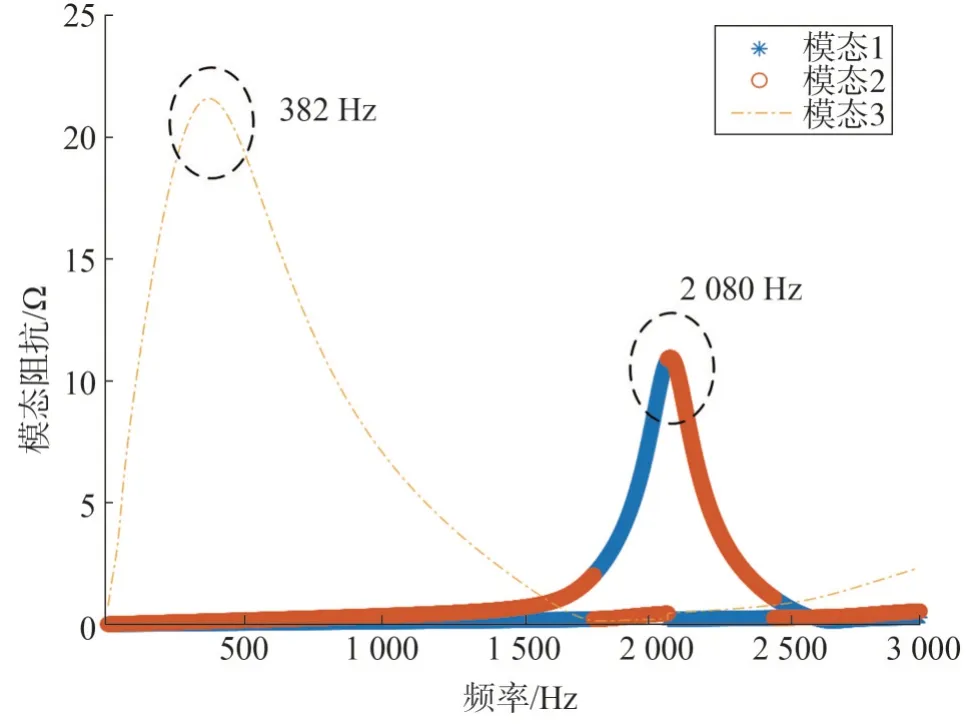
图6 多逆变器并网系统的谐振模态分析Fig.6 Resonance modal analysis of multi-inverter gridconnected system

观察图6，系统存在382 Hz 和2 080 Hz 两个谐振峰，表示在这两个频率点的模态阻抗值较大。所以在正常电流激励下，与一个较大的电阻值相乘，可能会出现较大的电压，即系统发生谐振。

通过观察比较，低频谐振峰是以382 Hz 为核心的谐振频率带，比高频谐振峰的峰值频带更宽。因此低频谐振峰发生时，可能会观测到邻近频段较大范围的一种谐波谐振现象，影响范围更广。高频谐振峰的尖峰频率范围较窄，如果发生该次谐振，对系统谐振频率的影响范围较窄，相对低频谐振峰而言，高频谐振峰的谐振定位更加精确。

由于导纳矩阵为三阶矩阵，所以对导纳矩阵进行对角化，所得的左、右特征向量矩阵也是三阶矩阵。将谐振峰对应频率带入导纳矩阵，可以得到如式（10）和式（11）所示系统左、右特征向量矩阵。根据参与因子的表达式（9），对左右特征向量进行合并，可以计算各个节点的参与因子值，如表2 所示。

382 Hz 处，模态3 发生谐振，系统左、右特征向量矩阵为

2 080 Hz 处，模态2 发生谐振，系统左、右特征向量矩阵为

由表2 可知，在382 Hz 处，各节点参与因子分布均匀，逆变器1 和2 的参与因子值都存在，即在该谐振频率，各节点的谐振可观测性和可激励性一致；在2 080 Hz 处，谐振由逆变器1 主导，逆变器2 的参与因子近似为零，PCC 点的参与因子较小但存在数值。可以发现，在不同的谐振频率处，系统各节点的参与因子表现存在差异，所以分析两个谐振峰在系统的谐振表现存在差异；但是各节点的参与因子数值和近似为1。

利用阻抗稳定判据［25］，与模态分析结果进行对比验证。将线路阻抗与滤波电感L2合并，进行谐振定位。如图7 所示。245 Hz，发生入网电流谐振，谐振频率属于模态分析所得低频谐振峰范围，相位裕度较大，无明显谐振现象；2 080 Hz，发生交互电流谐振，相位裕度较小，谐振现象明显。

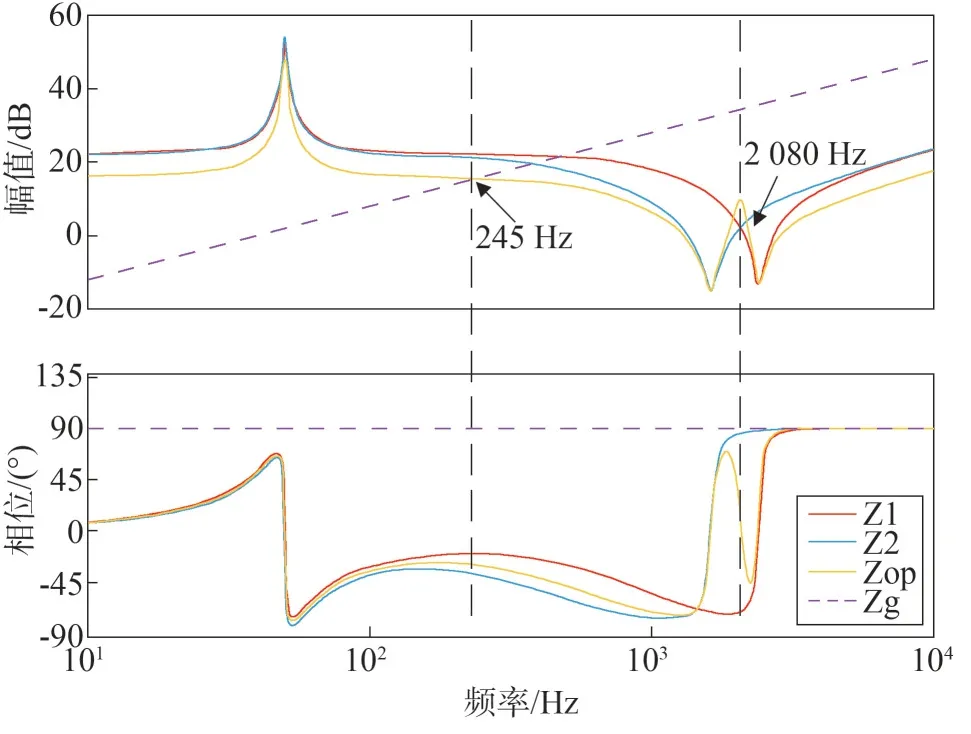
图7 逆变器输出阻抗和电网阻抗Fig.7 Inverter output impedance and grid impedance

多逆变器系统的谐振类型根据发生范围，可以分为两种：对电网侧和逆变器侧都会产生影响的系统谐振（入网电流谐振）、仅对逆变器侧产生影响的交互电流谐振。对谐振类型进行划分，有助于对参与因子表现所存在的差异进行理解。所以参与因子分布均匀的情况是入网电流谐振情况；各节点参因子都存在，且差异大的是交互电流谐振情况。

以两台1 型逆变器并联系统为例（组合2：0），经过上述分析，可以得到系统存在两个谐振频率，相应的参与因子表现如表3 所示。区别于不同型号并联情况，该情况下系统存在520 Hz 和2 400 Hz 两个谐振峰；在520 Hz 谐振频率处，各节点的参与因子分布均匀，逆变器1、2 的参与因子值都存在，即在该谐振频率，各节点的谐振可观测性和可激励性一致；但在2 400 Hz 谐振频率处，PCC 点的参与因子数值为零，仅逆变器侧参与因子数值存在，所以该谐振仅对逆变器侧产生影响。

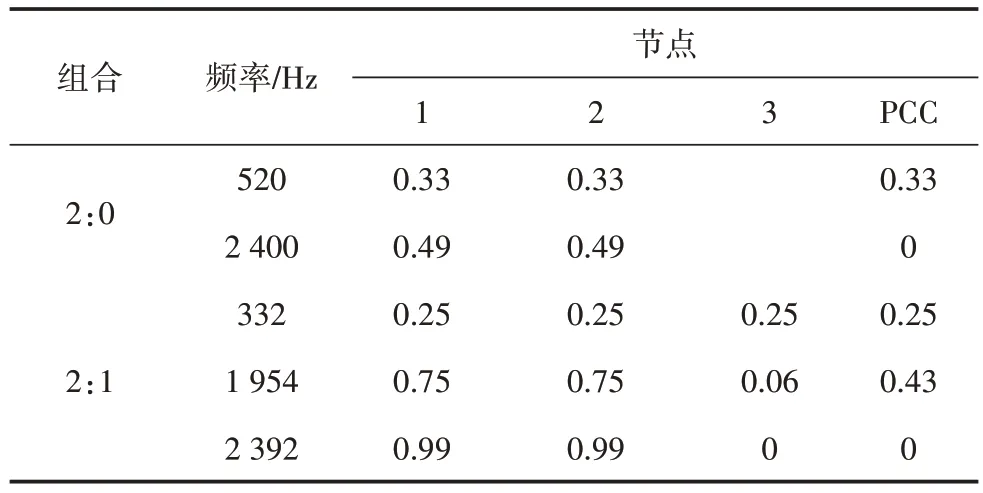
表3 关键模态下节点参与因子Table 3 Nodal participation factor of critical modes

当两台1 型逆变器和一台2 型逆变器并联（组合2：1），经过上述分析，可以得到系统关键模态下参与节点参与因子的表现，如表3 所示，存在3 种情况。332 Hz 和1 954 Hz 表现与1∶1 组合的表现一致，通过阻抗稳定判据的分析，332 Hz 为入网电流的谐振频率，相位裕度较大，无明显谐振现象；1 954 Hz为交互电流的谐振频率，相位裕度较小，有明显谐振现象；2 392 Hz 表现与2∶0 组合的表现一致，且谐振频率一致，所以该谐振频率为1 型逆变器之间的交互电流谐振频率，但是由于同型号逆变器的阻抗一致性，导致该类型谐振峰无相关谐振现象。

4 仿真验证

为验证上述方法及算例的正确性，根据表1 中所列的系统参数，在Simulink 中搭建仿真模型，进行仿真研究，结果如图8 所示。由图8（a）可知，当逆变器1 和逆变器2 并联运行时，可以发现并网电流不发生谐振。选取图8（a）的部分区域，进行局部放大，如图8（b）所示，可以看出，两个逆变器的输出电流中都含有高频谐波分量，但幅值相等、方向相反，从而在PCC 点相互叠加抵消，故并网电流不含高频谐波分量。当两台逆变器并联运行时，将逆变器2 在0.1s 切除，逆变器1 继续并网运行，由图8（c）可看出，逆变器1 输出电流的高频谐波分量消失。这说明高频谐波电流的产生是由两台逆变器并网运行的耦合效应产生的；当某台逆变器切除时，系统耦合状态发生变化，所以并联运行时发生的高频谐振消失。

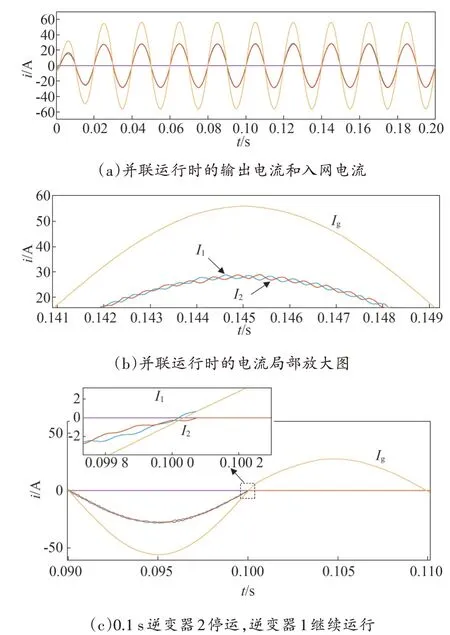
图8 逆变器1、2并联运行时，输出电流和入网电流波形Fig.8 Waveforms of output current and input-grid current when inverters 1 and 2 are operated in parallel

采用快速傅里叶变换（fast Fourier transform，FFT）对逆变器输出电流和电网电流进行分析，结果如图9 所示。由于一般生产应用多关注基波的整数倍，所以FFT 结果以基波的整数倍呈现，可能会与理论分析所得间谐波存在少许频率偏差，但是并不影响验证结论的正确性。并网电网电流不含高频谐波分量，而逆变器1 输出电流的高频谐波分量集中在2 050 Hz 频率附近，对应模态分析的谐振峰频率。虽然满足总谐波畸变率（total harmonic distortion，THD）低于5%的要求，但是针对各次谐波还存在具体的含量要求（1 650 Hz 以上谐波的限定为0.3%），该高频谐波含量超过了电流谐波限定的要求，对系统性能造成影响。对于低频段，并未出现明显的谐振现象，符合阻抗分析结果。证明了该模态方法谐振定位的准确性，参与因子分布均匀情况为系统谐振，对系统均存在影响；参与因子表现存在较大差异情况为交互电流谐振，仅影响逆变器侧。对组合2∶1进行仿真验证，结果如图10 所示，相关仿真结果关于谐振频率的定位，与理论分析一致。

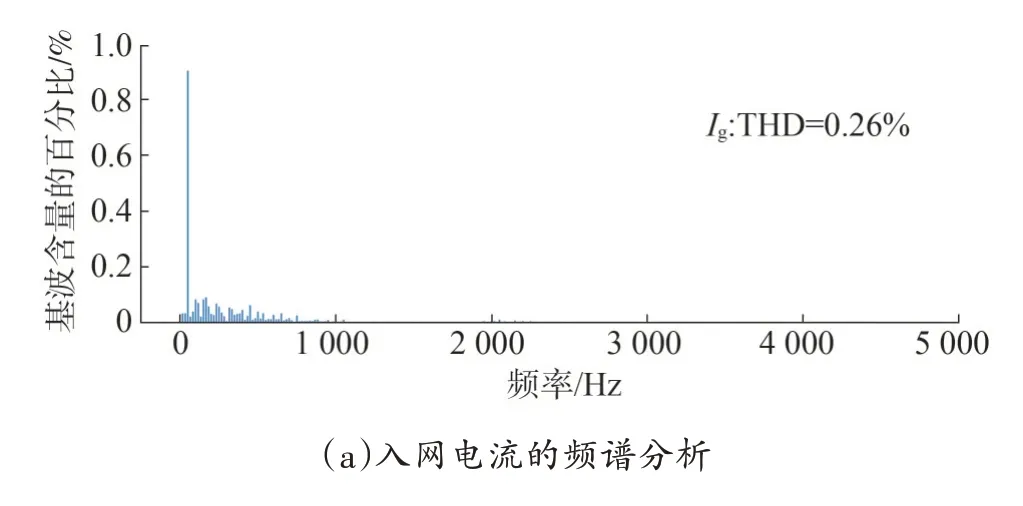
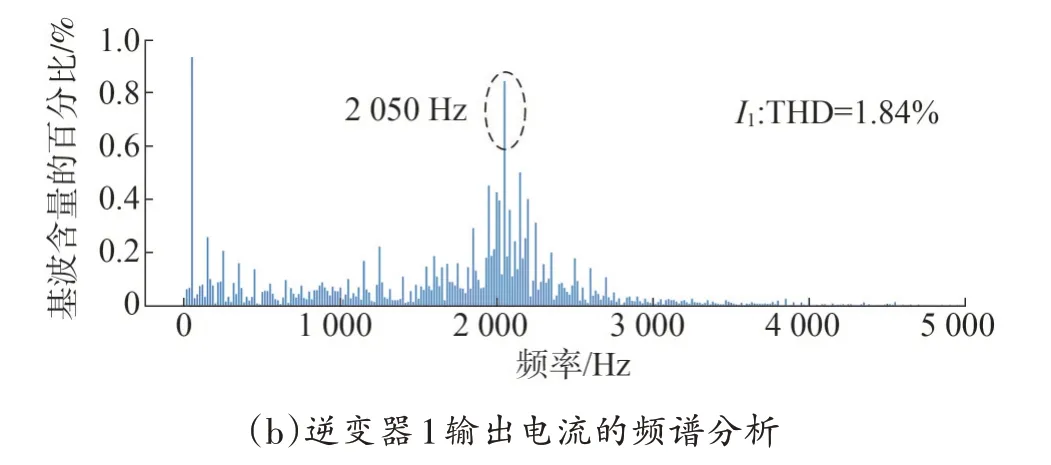
图9 逆变器1输出电流和入网电流的FFTFig.9 FFT results of output current and input-grid current in inverter 1

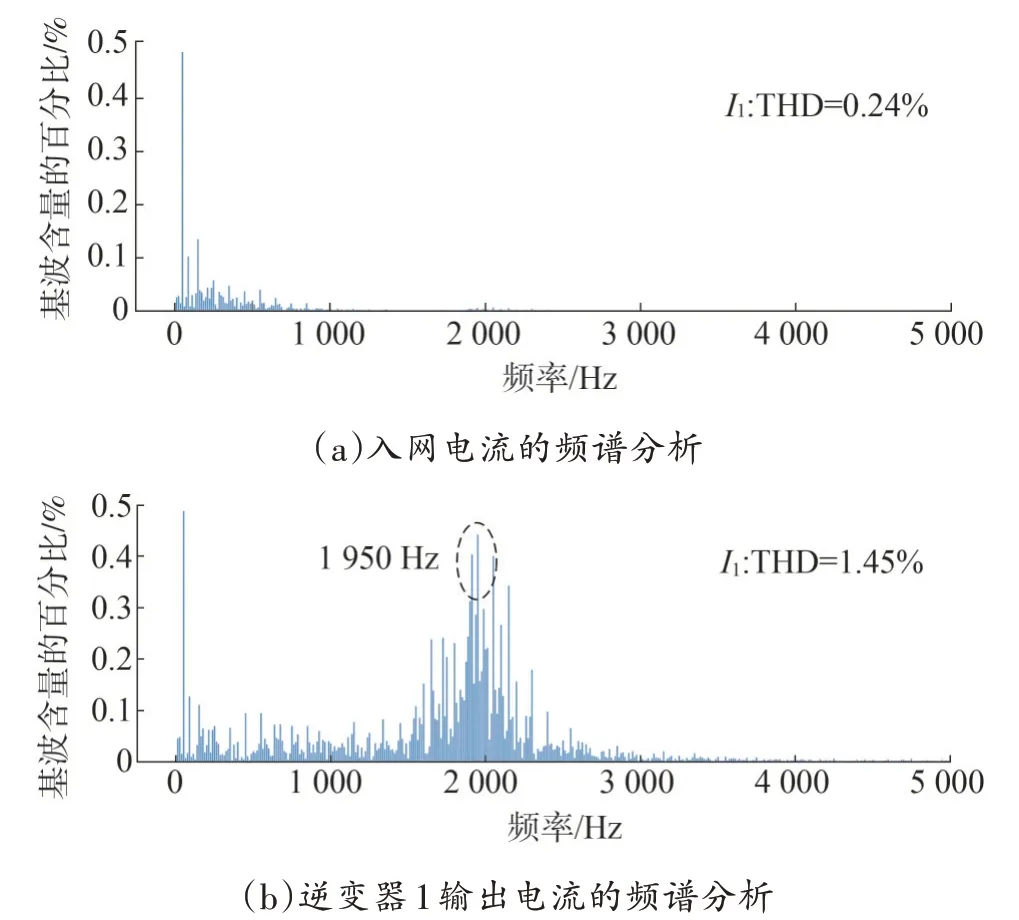
图10 组合2∶1时逆变器1输出电流和入网电流的FFTFig.10 FFT results of output current and input-grid current in inverter 1 when combination 2∶1

5 结束语

针对不同逆变器并联系统，提出一种基于模态分析的宽频带振荡风险区域定位方法，并在MATLAB/Simulink 搭建仿真模型，证实该方法的正确性和有效性。该方法根据逆变器参数、线路阻抗参数和电网阻抗参数，建立多逆变器系统的高阶导纳矩阵。通过对导纳矩阵等效变换，绘制模态阻抗随频率变化的曲线，得到系统的谐振频率。然后通过节点参与因子计算，根据参与因子表现确定其对应的谐振类型，结合不同类型谐振的特性，从而定位系统振荡的区域，利用模态分析所得参与因子来实现振荡区域定位。在新能源场站接入前，可利用该方法评估其可能存在的谐振频率及影响范围，或在新能源系统发生宽频带振荡事故后，利用该方法反向定位振荡区域。