基于CatBoost的新型电力系统两阶段轻量化暂稳智能评估方法
2024-03-04兰宇田张文栋刘世超仇玉强
兰宇田,姚 伟,张文栋,刘世超,仇玉强
(1.强电磁技术全国重点实验室(华中科技大学电气与电子工程学院),湖北 武汉 430074;2.国网山东省电力公司,山东 济南 250000)
0 引言
随着新型电力系统建设的推进,以风能为代表的新能源大规模并网,新能源的随机性、间歇性使得电力系统的运行条件越发难以预测。相比于传统电力系统,含高比例新能源的新型电力系统形态发生重大变化,稳定机理和特征更加复杂[1]。因此,针对新型电力系统开展快速且准确的电力系统暂态稳定评估(transient stability assessment,TSA)是当前的研究热点。
传统时域仿真法[2]和能量函数法[3]已经无法满足新型电力系统TSA 对时效性、准确性的要求。前者虽结果可靠但计算耗时长,后者虽求解迅速但结果偏于保守。近年来,随着广域测量系统(wide area measurement system,WAMS)和相量测量单元(phasor measurement unit,PMU)的发展,电力系统实时运行数据变得易于获取[4],以数据为驱动的机器学习方法成为当前最具发展前景的TSA 方法[5]。目前大量研究人员将机器学习与TSA 结合,如门控循环神经网络(gated recurrent neural network,GRU)[6-8]、长短期记忆网络(long short term memory network,LSTM)[9-11]、卷积神经网络(convolution neural network,CNN)[12-15]、生成对抗网络(generative adversarial network,GAN)[16-17],均取得了优异的指标效果。但这些研究大多都基于同步机主导的常规电力系统进行,新型电力系统由于新能源的随机性和间断性,表现出更为复杂的稳定机理,所以针对传统电力系统的研究在新型电力系统中具有一定的局限性。
此外,这些主流的机器学习方法都具有“黑箱”属性,即只了解模型的输入和输出,不清楚模型的内在逻辑或预测过程。可解释性弱、不透明等缺点,导致“黑箱”模型的不信任感。目前已经有部分文献尝试解决模型的“黑箱”属性,文献[18]基于模型无关局部解释(local interpretable model-agnostic explanations,LIME)算法对TSA 模型进行了事后解释,但LIME 算法基于随机扰动,存在解释不稳定的现象;文献[19]基于注意力机制,绘制了模型对特征的注意力热力图,但从中并不易获取模型具体关键决策量等知识;文献[20]基于沙普利值加性解释(shapley additive explanations,SHAP)算法对电力系统暂态电压稳定评估模型进行了事后解释,虽然其取得了相比于LIME 更佳的解释结果,但并未就获取的模型内在知识进行进一步的研究。所以如何解决数据驱动的“黑箱”属性和对模型内在知识进行进一步运用是当前研究的难点。
文中聚焦新型电力系统暂稳评估,首先提出了一种基于CatBoost(categorical boosting)算法的两阶段TSA 评估模型,解决了模型梯度偏移问题,实现了高质量新型电力系统暂态稳定判别。进一步地,使用Tree-SHAP 算法对所提出的包含粗判和精判的两阶段CatBoost 模型进行了事后解释,揭示了模型的预测过程,解决了模型的“黑箱”属性,并通过定量分析特征贡献度绝对均值,选取新型电力系统暂态评估的关键影响因素作为轻量化模型特征。最后,针对文献[20]未就模型内部知识进行进一步研究的问题,基于获取的暂态关键影响因素训练了低维CatBoost 两阶段模型,实现了模型的轻量化。
1 轻量化TSA智能评估框架
所提出的基于CatBoost 的新型电力系统两阶段轻量化暂稳智能评估方法主要分为两个部分:离线训练部分和在线评估部分,具体框架如图1 所示。其中离线训练部分包含CatBoost 暂稳评估模块、Tree-SHAP 解释与关键影响因素提取模块、低维CatBoost 暂稳评估轻量化模块共三个模块。
2 离线训练
离线训练部分需要学习大量新型电力系统运行数据,从而挖掘暂态稳定样本和失稳样本的特征,离线训练的流程如图2 所示,具体流程如下:
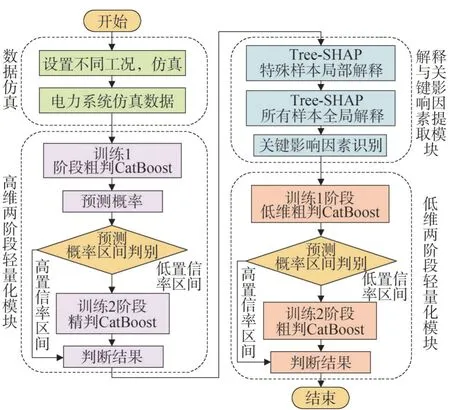
图2 基于CatBoost的新型电力系统两阶段轻量化暂稳评估模型离线训练流程Fig.2 Process of the two-stage lightweight transient stability intelligent assessment for new type power systems based on CatBoost
1)构建新型电力系统,通过设置不同运行工况进行时域仿真,获取仿真数据;
2)基于仿真数据训练1 阶段粗判CatBoost,选取低置信率区间样本重新训练2 阶段精判CatBoost;
3)基于Tree-SHAP 对两阶段评估模块从局部和全局两个角度进行解释,获取模型内部知识,即暂态关键影响因素;
4)基于Tree-SHAP 获取的知识,重新训练低维CatBoost 轻量化两阶段模型。
2.1 CatBoost暂稳评估模块
对于数据驱动的电力系统暂态稳定评估,需要通过有监督学习构建样本输入特征和输出标签之间的映射关系。文中基于CatBoost 算法进行暂稳评估。
CatBoost 是由俄罗斯Yandex 公司提出的一种由多棵对称决策树(oblivious trees,OT)串联组合而成的Boosting 集成学习算法[21],隶属于梯度提升树(gradient boosting decision tree,GBDT)算法框架。相比于其他GBDT 算法,能有效处理离散类别型特征的编码问题、梯度偏差问题和预测偏移问题,提升了模型的准确性和泛化能力。
在CatBoost 训练过程中,每次迭代均会生成一个弱学习器,最终得到强学习器,以此让整体模型损失函数达到最小值。假设在第t轮训练中,已经有训练好的前t-1 轮强学习器Ft-1(x) 损失函数为l(y,Ft-1(x))。本轮的目标就是加入新的弱学习器ht(x),使得本轮损失函数最小。第t轮迭代的目标函数即弱学习的参数如式(1)所示。
式中:y为样本标签;E为期望函数;x为输入样本。
由于是沿着损失函数下降最快方向进行迭代,所以每一轮损失的近似值由损失函数的负梯度-gt(x,y)表示,如式(2)所示。
将式(2)带入式(1)得
最终得到第t轮强学习器Ft(x)。
式中:lr为每一轮迭代的学习率。
但在每一轮迭代过程中,使用的梯度都是由相同的训练样本xtrain进行计算的,但实际上与所有样本x之间存在一定的偏差,即梯度偏差。CatBoost 算法为解决该问题造成的模型精度下降,对GBDT 算法进行了改进:在第t轮迭代过程中,令gk(xk,yk)为在本轮第k个样本(xk,yk)上的损失函数梯度值。为使gk(xk,yk)无偏于模型Ft-1,首先使用前k-1 个样本重新训练代理模型Mk,再基于代理模型Mk来估计xk上的梯度。这样每个样本的梯度都是通过不包含该样本的其他样本进行计算的,进而解决了梯度偏差问题。具体数学证明可参考文献[21]。
2.2 解释与关键影响因素提取模块
CatBoost 两阶段模块在未轻量化之前需要采集电力系统的几乎所有电气特征,数据量大,传输时间长,在实际电力系统中几乎无法应用。所以需要对模型进行轻量化,减少模型的输入特征。
事后解释算法Tree-SHAP[22]基于合作博弈论,具有局部精度、对称性、无效性和可加性四种特征[23],是目前理论最优的归因算法之一。使用Tree-SHAP 算法能透明化模型的决策过程,挖掘模型的内在关键影响因素,进而指导模型在维持评估精度的前提下减少输入特征的数目。
合作博弈论认为单纯按照每个玩家固定收益对总收益进行分配是不合理的,故提出了以边界贡献(marginal contribution,MC)作为分配指标的收益分配思路。在电力系统中,定义游戏G为暂态稳定评估模型,玩家P为模型的各个输入特征。可通过式(5)来计算特征对暂稳评估结果的贡献度,即Shapley 值。
由于模型的输入特征过多,特征子集有151!个,极难计算。所以针对树模型的特有结构特性,研究人员提出了两种简化思路,实现了Shapley 值的快速计算。
1)简化方向1。
通过树结构来评估特征贡献。根据Shapley 值的可加性特征,绘制出一种可能的特征子集编码情况中模型预测的预期变化,如图3 所示。

图3 模型预测期望变化Fig.3 Expectation changes based on model prediction
所以,为求解特征i的Shapley 值ϕi,就只需要求解f{x1,x2,…,xi-1}({x1,x2,…,xi-1}) 和f{x1,x2,…,xi}({x1,x2,…,xi})的差值,而树结构中对具有缺失值的数据条件期望的求解是简单的,因为其会忽略缺失值所在的叶节点。通过这样简化来计算特征子集的特征p的Shapley 值,只需要遍历每一棵树的每一个节点。此时,Tree-SHAP 时间复杂度为O(TL2M),其中T为树的总数,L为总节点数目,M为特征数目。
2)简化方向2。
按照树结构进行遍历。通过简化方向1,可以将不同特征组合输入,简化求解各个特征的贡献度,但特征组合依然是2M个。简化方向2 的大致思路为不遍历所有特征组合,而是只需要遍历树的所有路径,在遍历的过程中记录路径信息,在叶节点处求解这条路径的特征贡献。因为从树的路径角度来看,在中间节点除了其判断条件以外,其他特征的引入对树的决策是不会有任何改变的,这些特征组合均不用考虑。
3 在线评估
获取电力系统实时数据,对离线训练获取的暂态关键影响因素进行采集,形成样本j的模块输入矩阵Xj=[x1,j,x2,j,…,xn,j]。首先,将输入矩阵输入1 阶段粗判CatBoost 进行暂态稳定状态预测,并获取预测为稳定的概率值Pj;其次,对Pj进行分析,如果Pj属于预先设定的高置信区间则直接输出预测结果,如果Pj落入低置信率区间,则说明该样本为1 阶段粗判CatBoost 的边界样本,需要2 阶段精判CatBoost模型给出预测结果。评估流程如图4 所示。
研究人员称,父母对于子女日后的语言表达能力也起着十分重要的作用。所以婴儿期坚持给宝宝“磨耳朵”,日后会有意想不到的收获哦!
4 算例研究
所提出的基于CatBoost 的两阶段电力系统暂态稳定评估和其可解释性研究是基于仿真数据进行分析的,研究系统为接入高比例风电的IEEE 39 节点系统。算例研究的硬件平台为CPU Intel® Core(TM)i9-10900K @3.70 GHz,RAM 64 GB,GPU NVIDIA Geforce RTX 2080 Super,电力系统时域仿真基于PSASP 软件实现,机器学习模型基于Scikitlearn1.3.0 搭建。
4.1 样本生成
IEEE 39 节点系统也被称为新英格兰10 机电力系统,对于含风电的IEEE 39 节点电力系统,有5 台发电机、4 个风电场、39 根母线、46 条支路、12 台变压器和19 个负载,其拓扑结构如图5 所示,图中G表示发电机,其中G1 表示多个发电机,WF 表示风电场。
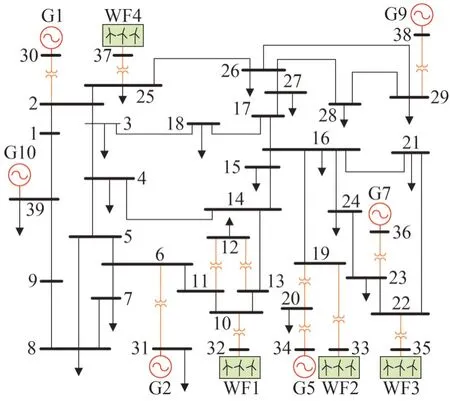
图5 含风电的IEEE 39节点电力系统Fig.5 IEEE 39 bus power system with wind power
为覆盖尽可能多的电力系统运行工况和故障发生情况,可以通过以下操作实现:设置潮流水平在85%~115% 之间波动,设置为85%、90%、95%、100%、105%、110%、115%;故障设置为三相金属性短路并切线(N-1),故障线路遍历IEEE 39 系统中所有的非变压器支路,故障位置为每一条线路全长的2%、25%、50%、75%、98%,故障时间设置为0.1 s、0.2 s、0.3 s、0.4 s、0.5 s。具体生成方案如表1 所示,这样可以较为全面地覆盖系统运行工况和故障发生的可能性。仿真时间设置为10 s,剔除部分数据异常样本,最终生成5 873 个样本。
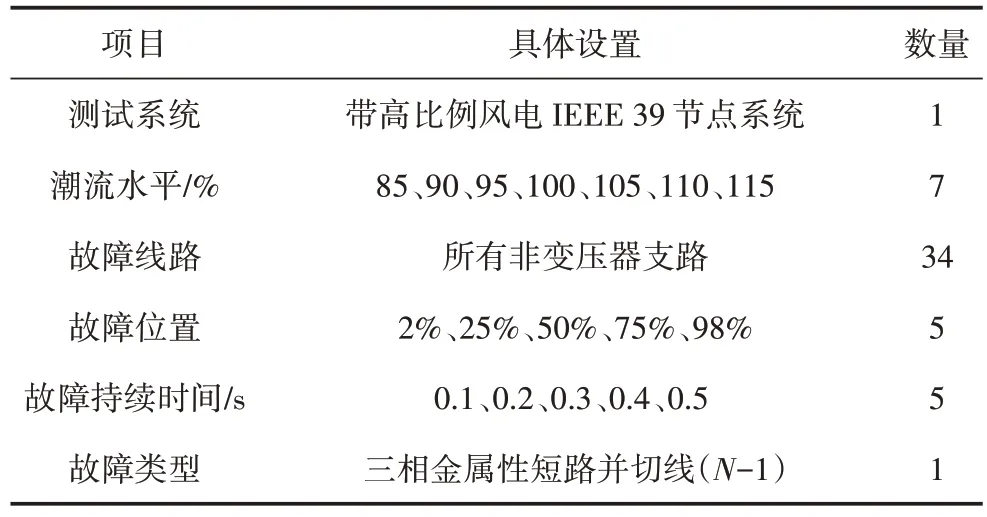
表1 IEEE 39节点系统样本生成方案Table 1 IEEE 39 system sample generation solution
4.2 特征选择与标签标注
为提高模型的准确率,采集所有能观测或能计算的电气特征,采集时间定为故障切除后的下一时刻,具体特征如表2 所示。

表2 样本具体电气特征量Table 2 Sample specific electrical characteristic quantity
表2 中共计采集151 个特征量构成样本的模型输入数据,样本标签由暂态稳定指数(transient stability index,TSI)确定[24]:
式中:|Δδ|max为在仿真时间内,任意两台发电机相对功角差值绝对值的最大值;STI为暂态稳定指数,STI>0 说明该样本为稳定的;STI<0 说明该样本为失稳的。最后得到稳定样本共计3 514 个,失稳样本共计2 359 个。
4.3 CatBoost两阶段评估模块
将全体样本分为70%、15%、15%三部分,分别作为训练集、验证集和测试集。通过训练集训练CatBoost 模型,再根据验证集调整参数,最后在测试集上测试模型效果。
根据2.1 节中简述的CatBoost 原理训练一阶段粗判TSA 模型,其结果的混淆矩阵如图6 所示。
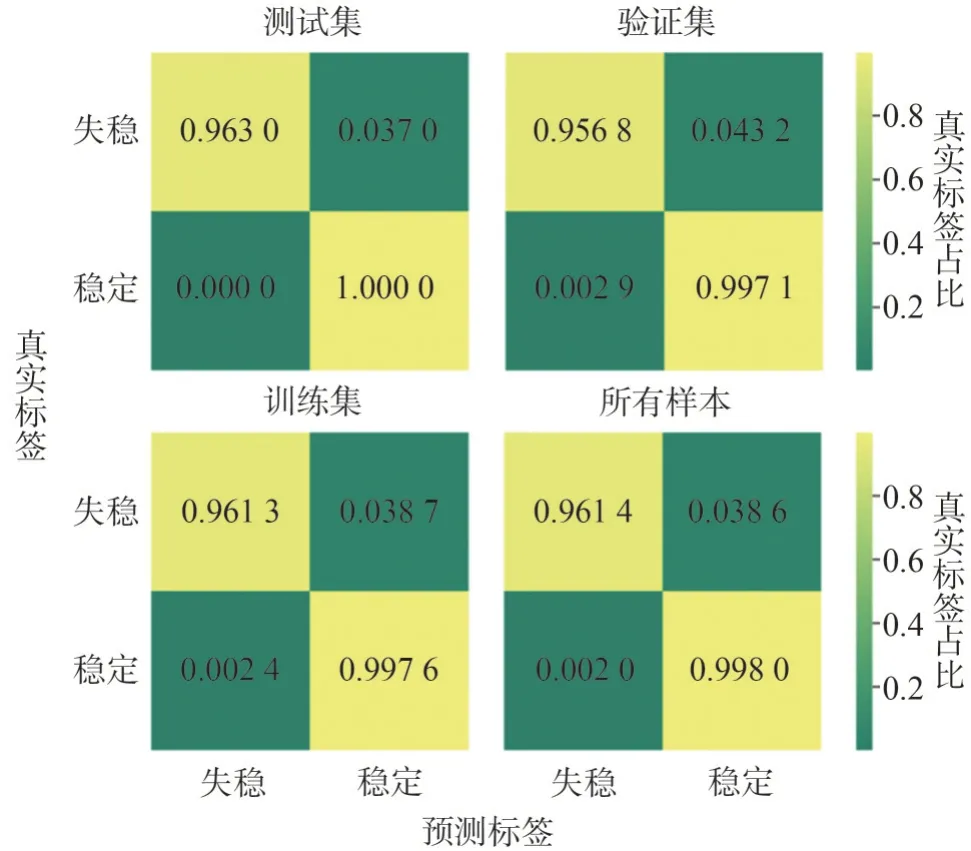
图6 一阶段粗判TSA模型混淆矩阵Fig.6 One-stage prediction segment TSA model confusion matrix
一阶段粗判TSA 模型在所有样本中仅取得了98.33%的准确率。为进一步提升模型的准确率,首先绘制模型对所有样本判断为稳定的预测概率散点图,如图7 所示。

图7 一阶段粗判TSA模型预测概率散点图Fig.7 Scatter plot of predicted probabilities for first-stage preliminary TSA
从图7 中,不难发现:预测概率大于0.6 或小于0.2 时,模型识别准确率极高;但在大于0.2 且小于0.6 的部分,准确率出现了下降。这是因为模型在训练过程中,会更加偏向于大众样本;对于决策边界附近的样本,由于正则化的存在,会使得模型精度下降。对于大模型,更希望其决策边界更加光滑,所以降低正则化参数的操作是不可取的。
为识别这些特殊边界样本的特征,可以构建二阶段精判TSA 模型。从低置信区中筛选出判别错误的样本,重新构成新的训练集、验证集、测试集,注意筛选前后样本类别须保持一致。基于这些样本重新训练能识别特殊样本的精细化评估模型,其训练结果和常见模型评价指标[19]结果如表3 所示。
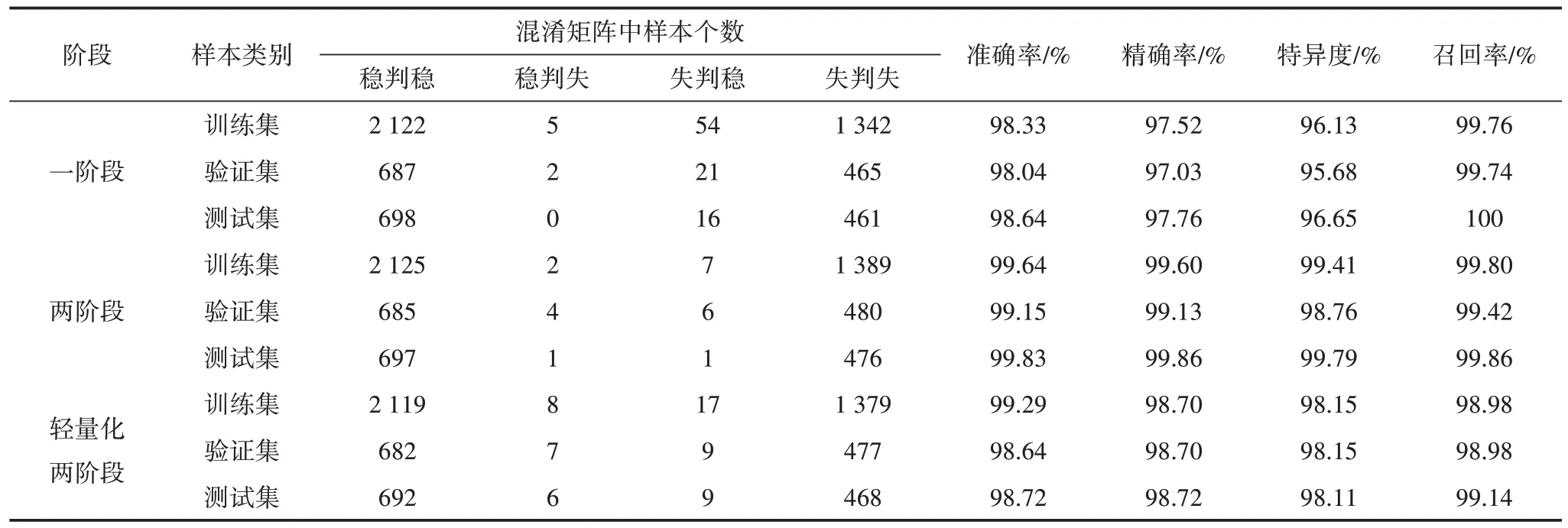
表3 基于CatBoost的新型电力系统两阶段暂稳评估模型指标Table 3 Indicators for the two-stage transient stability assessment model in new type power systems based on Catboost
基于表3,可以发现两阶段TSA 评估模型指标,除测试集的召回率外,全面优于一阶段模型。因此可以认为,引入二阶段精细化评估边界样本能有效提高CatBoost 模型的判断准确度。类似地,再对比其他机器学习模型,包括XGBoost[25]、随机森林[26]、支持向量机[27]和决策树[28],模型常见评价指标[19]对比如图8 所示。
4.4 模型事后解释
利用Tree-SHAP 算法对模型预测结果进行事后解释,首先分析单个样本。随机选取第8 号、第13号样本。前者预测为稳定的概率为10.11%,直接由一阶段粗判模型给出失稳判断结果,其透明化的预测过程如图9 所示;后者预测一阶段预测为稳定的概率为55.13%,为边界样本,落入二阶段精细判断模型,二阶段模型的预测过程如图10 所示。通过Tree-SHAP 算法,可以直观感受模型的决策过程,提高模型的可解释性,挖掘模型的内在知识。
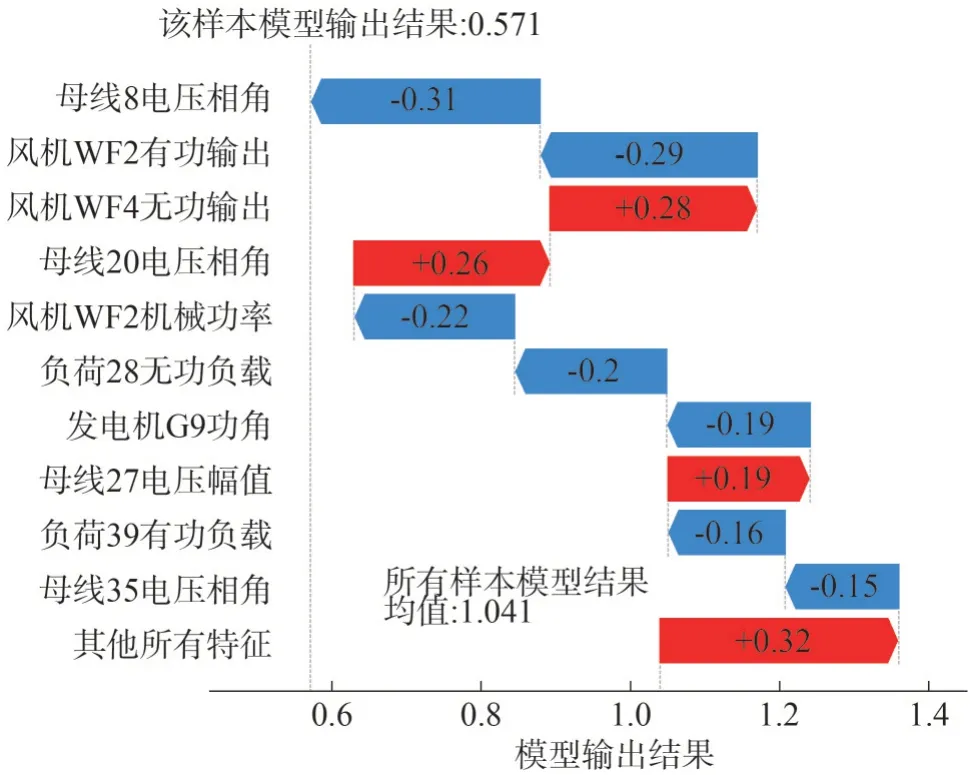
图9 第8号样本的决策过程Fig.9 Decision-making process for sample No.8
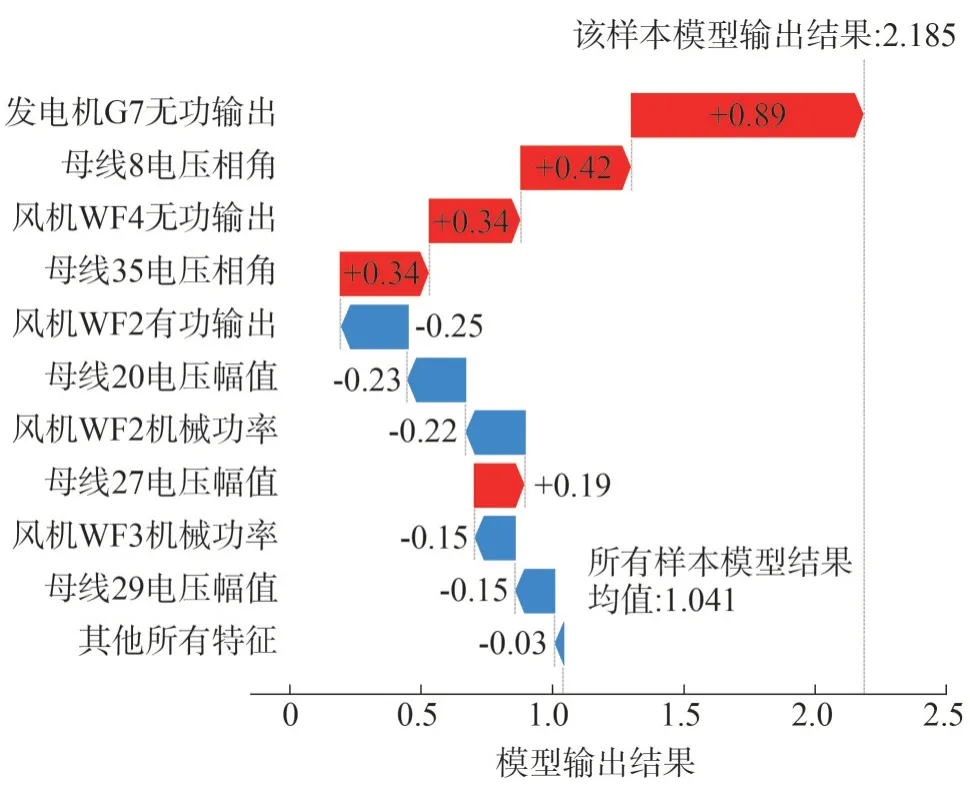
图10 第13号样本的决策过程Fig.10 Decision-making process for sample No.13
对于每一个样本都可以分析出其决策过程,挖掘哪些特征对决策做出了重要贡献。再从全局角度分析,计算如式(7)所示的m个样本的所有特征绝对贡献均值mean(||ϕ),就能得出模型主要侧重于哪些重要特征,进行电力系统暂态稳定域的关键影响因素的挖掘,具体前20 个关键影响因素如图11 所示。
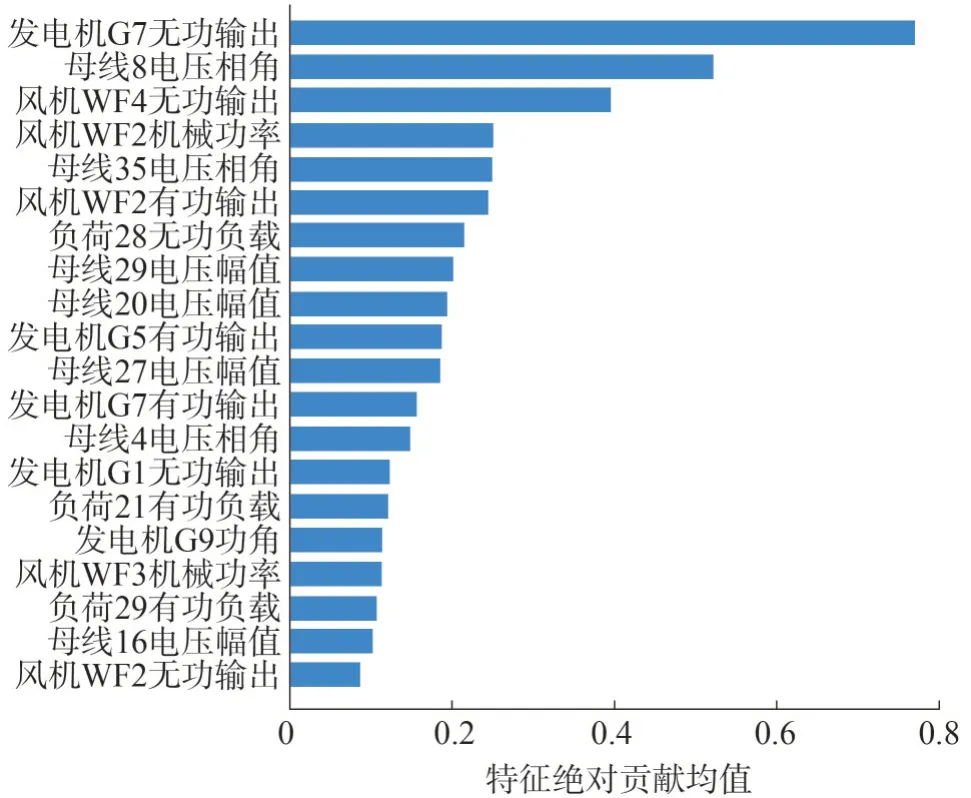
图11 暂态关键影响因素Fig.11 Key transient influencing factors
4.5 低维CatBoost两阶段验证模块
模型的效果与选择的特征之间存在紧密联系,可选择筛选出来的前30 个关键影响因素重新训练CatBoost 两阶段评估模型,依据其训练结果来间接证明识别效果的有效性,其训练结果如表3 所示。
从表3 可以发现进行特征选择后的低维CatBoost 两阶段评估模型只用了20%的特征量就达到甚至超过了一阶段CatBoost 评估模型的效果。对比原始两阶段评估模型,模型在测试集上的准确率仅下降了1.11%,也远超于其他算法,所以暂态关键影响因素的识别效果比较优秀。为继续探究低维CatBoost 的模型效果低于高维模型的原因,绘制低维一阶段模型预测概率散点图如图12 所示。
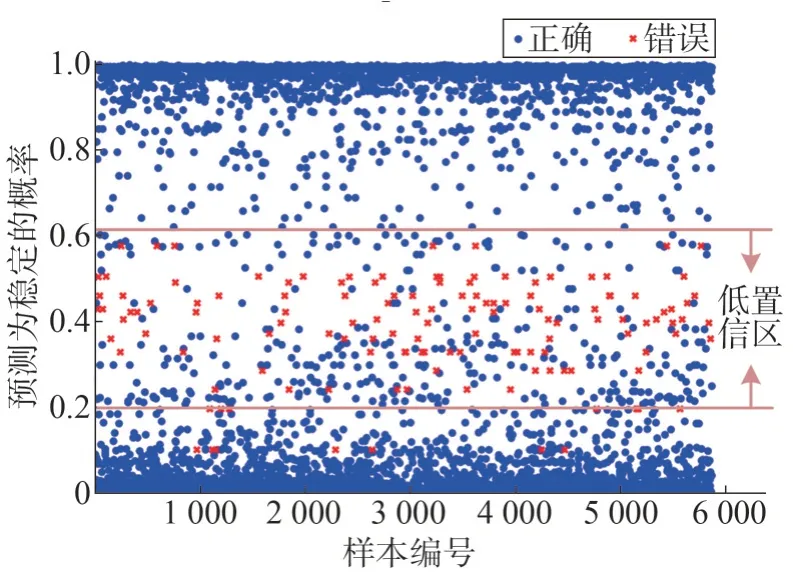
图12 低维一阶粗判TSA预测概率散点图Fig.12 Scatter plot of predicted probabilities for low-dimensional first-stage preliminary TSA
根据图12 可以发现,由于低维CatBoost 特征维度有限,低置信区错判样本明显增多,而且边界样本数目上升,导致二阶段识别的边界样本特征也有限,最终导致了效果低于高维模型。
5 结论
暂态稳定分析是新型电力系统领域的研究重点,传统暂稳分析方法在时效性和准确性上略有欠缺。机器学习技术目前在各个领域取得了巨大的成果,将其与新型电力系统暂态稳定评估结合拥有广阔的前景。文中针对TSA,构建了具有高质量指标的评估模型,并基于机器学习可解释性算法提取模型内在知识,实现了模型的轻量化,具体创新点如下:
1)针对单层CatBoost 评估模型指标精度不足的问题,设计了粗判加精判两阶段CatBoost 评估模型,取得了模型指标的全面提升;
2)针对模型可解释性不足的问题,引入Tree-SHAP 算法,实现了模型决策过程的透明化,并从中获取了模型的内在知识,即暂态关键影响因素;
3)针对TSA 模型输入特征量大、参数多的问题,基于暂态关键影响因素训练了低维两阶段轻量化CatBoost 模型,以20%的特征数量实现了超越单层CatBoost 评估模型的评价指标。
文中采用的是仿真软件获取的时域仿真数据,与实际中基于PMU 测量获取的数据还存在一定的差距;仅针对新型电力系统暂态稳定的评估问题,但事后控制并未涉及,如何基于模型解释结果进行控制也值得深入研究。
