基于卡尔曼和扩展卡尔曼滤波的耦合载波跟踪方法*

付学瀚，燕贺云，朱立东，蒯小燕，郭孟泽

（电子科技大学通信抗干扰全国重点实验室，四川 成都 611731）

0 引言

高动态环境下，通信双方的相对运动速度较高，此时，反映到信号层面上则表现为强多普勒效应，即接收信号存在较大的载波频率偏移且载波频偏具有一定的高阶变化率，为了精确跟踪载波相位，传统的方法是将锁频环和锁相环联合使用[1-3]，通过增大环路带宽来适应大范围的多普勒频偏，然而环路带宽的加大又势必导致载波跟踪精度的降低，尤其当跟踪环路处于低信噪比通信环境中时，噪声的引入甚至会导致载波跟踪环失锁。因此，在低信噪比高动态环境下，传统载波跟踪环路的可承受的动态范围与跟踪精度之间需要进行权衡[3-6]。

在此背景下，卡尔曼滤波（KF,Kalman Filter）[7]在载波跟踪领域的应用受到了很大的关注。文献[8-10]对基于卡尔曼滤波的载波跟踪环路进行了性能分析，表明基于卡尔曼滤波的载波跟踪环路可以自适应地改变环路带宽，因此具有更好的跟踪性能。文献[11-12]考虑了数控振荡器（NCO,Numerical Controlling Oscillator）的反馈，提出了基于鉴相器辅助的卡尔曼滤波跟踪环路，但跟踪性能受到鉴相器的限制。文献[13]给出了基于扩展卡尔曼滤波（EKF,Extended Kalman Filter）[14]的载波跟踪算法，但是没有考虑积分-清除[15]处理后的情况。文献[16]提出了一种基于无迹卡尔曼滤波（UKF,Unscented Kalman Filter）[17]的载波跟踪算法，在低信噪比环境下跟踪性能相较于传统载波跟踪算法有很大提高，但跟踪精度还有进一步的提升空间。

为了进一步提高低信噪比高动态环境下载波跟踪算法的跟踪性能，本文在传统锁频环辅助锁相环的结构基础上，分别以卡尔曼滤波器代替锁频环的环路滤波器和扩展卡尔曼滤波器代替锁相环的环路滤波器和鉴相器设计了一种新的耦合载波跟踪环路。最后通过仿真验证，证明本文提出环路的跟踪性能优异，且显著优于传统环路。

1 基于卡尔曼滤波与扩展卡尔曼滤波相结合的载波跟踪环路

本文中，不考虑数据位的影响，将接收信号建模为数字中频载波信号。基于卡尔曼滤波与扩展卡尔曼滤波相结合的载波跟踪环路结构如图1 所示：

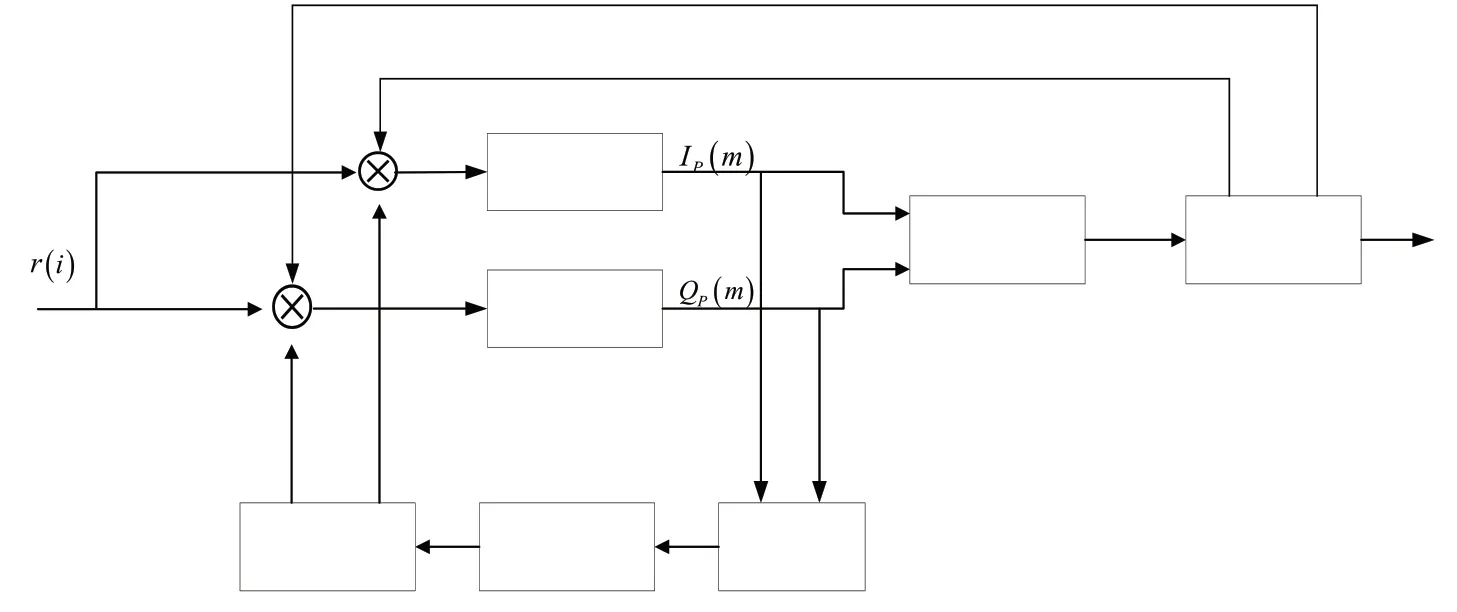
图1 基于卡尔曼滤波与扩展卡尔曼滤波相结合的载波跟踪环路结构

假设接收到的数字中频信号为：

其中，A为输入信号载波幅度，fIF为输入信号载波的中频频率，fd为多普勒频偏，φ0为输入信号载波的初始相位，n(i)为高斯白噪声。

输入信号经过混频器与积分器后，结果为：

其中，Δfd为输入信号载波和本地生成载波间的频率差，N为每次相干积分所需的采样点数，Ts为采样时间，为输入信号载波与本地生成载波在相干积分时间内的平均相位差。

基于卡尔曼滤波的锁频环，需要使用鉴频器来鉴别输入信号载波的多普勒频偏与其估计之间的误差。在本文中，采用在高信噪比与低信噪比环境下均有较好鉴频特性的四象限反正切鉴频器[18]。叉积cross、点积dot与鉴频计算方法的数学表达式为：

2 系统方程设计

2.1 基于卡尔曼滤波的锁频环系统方程设计

卡尔曼滤波实质上是贝叶斯估计原理对于观测向量在基于线性最小均方误差准则情况下的递归解，即理论上其滤波输出为输入信号多普勒频偏的最优估计值。

根据卡尔曼滤波的线性化方法，分别对通信终端不存在径向加加速度和存在径向加加速度的两种高动态运动模型，分别推导了频率斜升信号模型和频率加速信号模型系统方程。

（1）频率斜升信号的系统方程

不存在径向加加速度的运动模型，其多普勒频偏可以建模为频率斜升信号模型：

其中，fv为输入信号初始时刻的多普勒频率，fa为多普勒频率一阶变化率。

对于不存在径向加加速度的运动模型，可以建立二阶线性系统方程来估计多普勒频偏[4,7]。卡尔曼滤波在锁频环中的状态方程和观测方程可以表示为：

系统的状态转移矩阵和测量矩阵表示为：

卡尔曼滤波分为预测和校正过程，根据式(8)和式(9)所确定的状态方程和观测方程，卡尔曼滤波的具体过程如下：

预测过程：

校正过程：

其中，K为卡尔曼滤波增益，Pm为状态向量的预测协方差矩阵，Q 和R 分别为W 和V 的协方差矩阵，表示为：

（2）频率加速信号的系统方程

存在径向加加速度的运动模型，其多普勒频偏可以建模为频率加速信号模型：

对于存在径向加加速度的运动模型，可以建立三阶线性系统方程来估计多普勒频偏[4,7]。此时，状态方程和观测方程的表示形式同式(8) 和式(9)。状态向量变为，分别表示多普勒频偏、多普勒频偏一阶变化率和二阶变化率。

系统的状态转移矩阵和测量矩阵表示为：

卡尔曼滤波过程同式(12) 至式(16)，此时观测噪声协方差矩阵R 同式(18)，噪声协方差矩阵Q 表示为：

2.2 基于扩展卡尔曼滤波的锁相环系统方程设计

在低信噪比环境下，无论是对于频率加速信号还是频率斜升信号，基于卡尔曼滤波器锁频环的输出含有多普勒一阶变化率的残差，因此，还需要具有三阶卡尔曼滤波器的锁相环来跟踪载波相位。相较于传统卡尔曼滤波，扩展卡尔曼滤波可以直接以积分器的输出来作为观测向量，且基于扩展卡尔曼滤波的跟踪环路不需要鉴别器，环路性能不受鉴别器的限制，能够接受更高的动态范围且更能适应低信噪比环境，因此，锁相环基于扩展卡尔曼滤波来设计。

假设锁相环输入信号在第m-1 个积分时间段T初始时刻的相位为，载波多普勒频偏fd(m-1)，多普勒一阶变化率fa(m-1)，则输入信号在第m个积分时间段初始时刻相位为：

由此，可以将状态方程表示为[19]：

扩展卡尔曼滤波直接以积分输出结果作为观测量来建立观测模型，因此，观测方程表示为：

扩展卡尔曼滤波算法中线性化观测矩阵Hm为：

扩展卡尔曼滤波同样分为预测和校正过程，根据式(31) 和式(34) 所确定的状态方程和观测方程，扩展卡尔曼滤波的具体过程如下：

预测过程：

校正过程：

其中，过程噪声协方差矩阵Q 同锁频环中三阶卡尔曼滤波器的形式相同，观测噪声协方差矩阵R 表示为：

根据滤波结果，调整本地生成载波的相位和频率。用于第m+1 个积分时间段的本地生成载波在中频频率基础上的频率偏移和第m+1 个积分时间段的本地生成载波初始时刻相位为：

3 仿真分析

为了验证本文所提出的载波跟踪环路的性能，分别从频率斜升信号和频率加速信号两种信号模型进行仿真验证，并分别与传统跟踪环路进行性能比较。系统的仿真参数如表1 所示：

表1 系统仿真参数[20]

3.1 对频率斜升信号的跟踪性能

输入信号的初始多普勒频率取为1 kHz，多普勒一阶变化率取为10 kHz/s，信噪比为-20 dB。在高动态环境下，传统方法通常使用基于环路滤波器的二阶锁频环结合三阶锁相环的载波跟踪环路来跟踪频率斜升信号，因此，在仿真中将本文提出的载波跟踪环路同传统二阶锁频环结合三阶锁相环的载波跟踪环路。多普勒频率跟踪误差和相位跟踪误差如图2 和图3 所示：

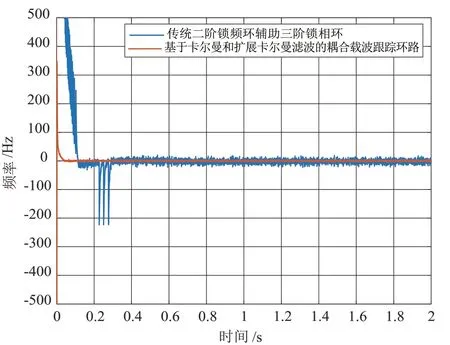
图2 频率跟踪误差

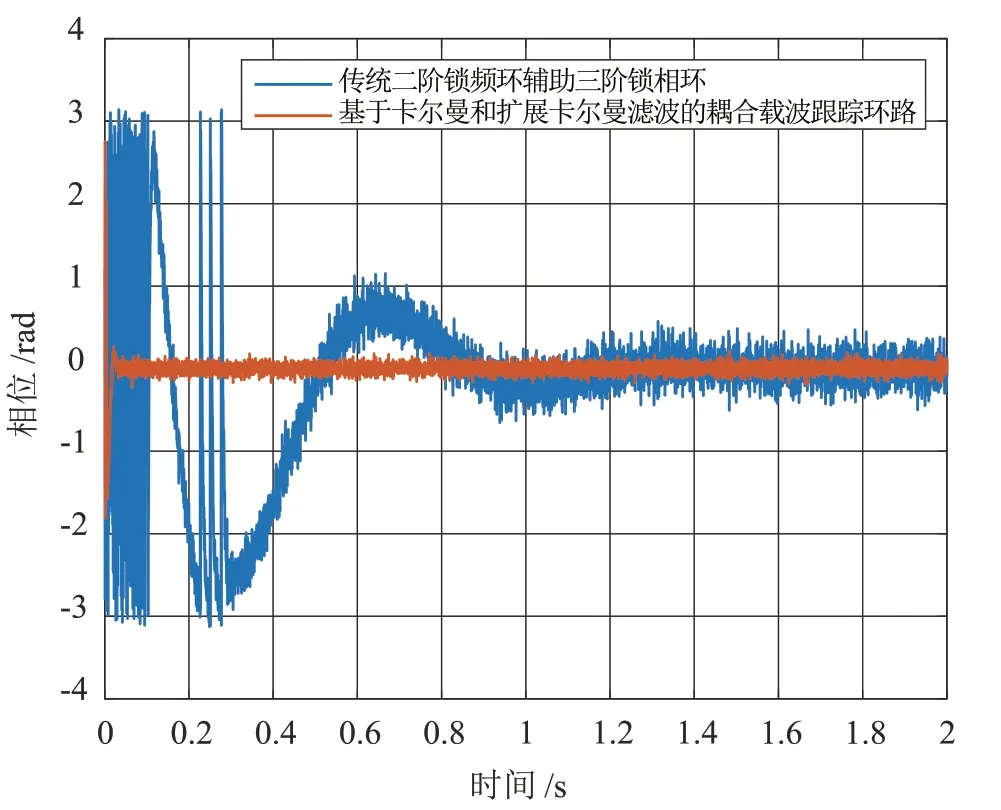
图3 相位跟踪误差

如图2 和图3 所示，本文所提出的载波跟踪环路跟踪性能稳定，跟踪精度高且收敛速度很快，环路收敛时间小于60 ms，频率跟踪误差在5 Hz 以内，相位跟踪误差在0.25 rad以内，而传统的二阶锁频环结合三阶锁相环的跟踪环路的收敛时间为1.2 s，且频率和相位跟踪误差波动较大，最大可达到22 Hz 和0.45 rad。所以对频率斜升信号跟踪时，本文所提出的载波跟踪环路相较于传统环路跟踪性能有较大提升。

图4 和图5 为环路达到收敛状态时，不同信噪比下的频率和相位的RMSE（均方根误差曲线），比较了本文提出的载波跟踪环路和传统的二阶锁频环结合三阶锁相环的跟踪环路在不同信噪比下的跟踪性能。在信噪比-20～-10 dB 的范围内，由系统热噪声引起的频率和相位的均方根误差不断减小，高动态环境导致的动态应力误差为误差的主要来源。由图4和图5 可知，本文所提出的载波跟踪环路跟踪性能在低信噪比环境下显著优于传统的二阶锁频环结合三阶锁相环的载波跟踪环路。随着信噪比的提升，传统环路的跟踪性能不断接近本文所提出跟踪环路的性能。

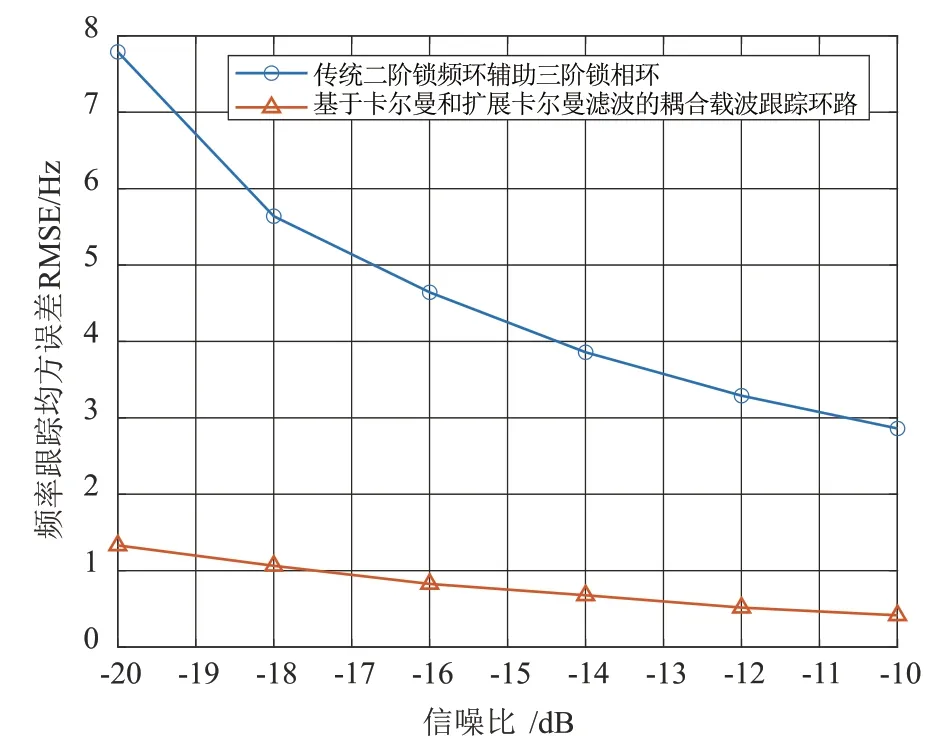
图4 不同信噪比下频率均方根误差

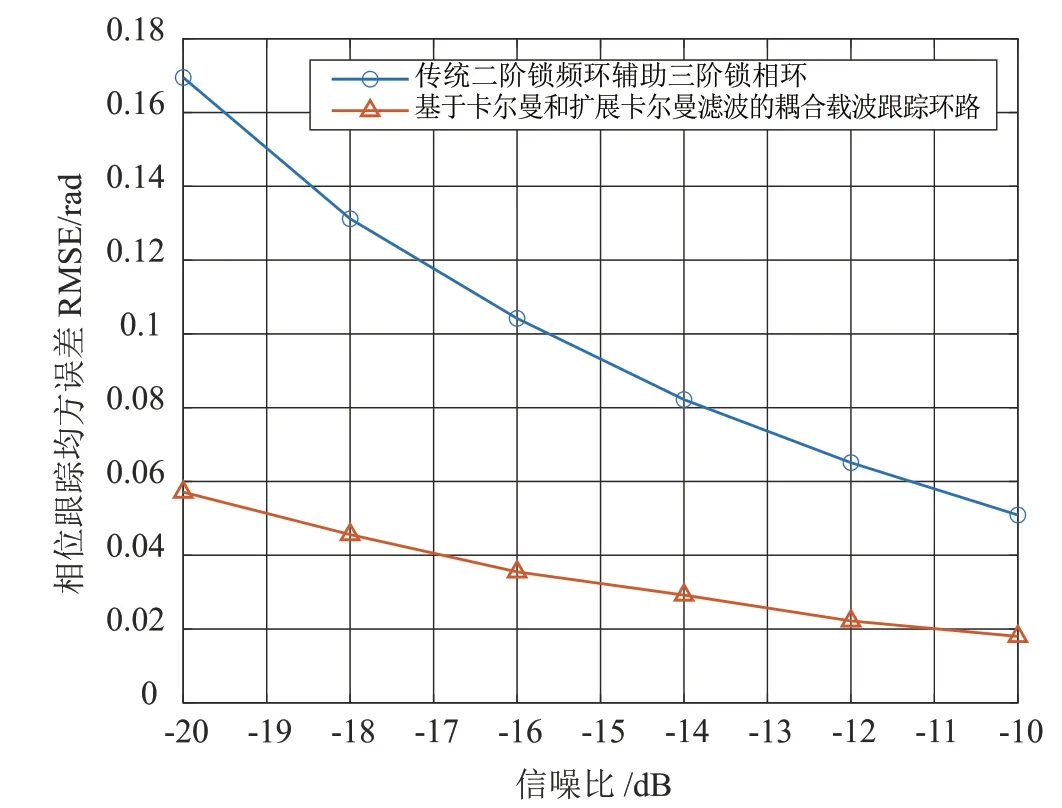
图5 不同信噪比下相位均方根误差

3.2 对频率加速信号的跟踪性能

输入信号的初始多普勒频率取为800 Hz，多普勒一阶变化率取为10 kHz/s，多普勒二阶变化率50 Hz/s2，信噪比为-20 dB。在高动态环境下，传统方法通常使用基于环路滤波器的三阶锁频环结合四阶锁相环的载波跟踪环路来跟踪频率加速信号，因此，在仿真中将本文提出的载波跟踪环路同传统三阶锁频环结合四阶锁相环的载波跟踪环路。多普勒频率跟踪误差和相位跟踪误差如图6 和图7 所示：

图6 频率跟踪误差

图7 相位跟踪误差

如图6 和图7 所示，虽然环路阶数提升，但本文提出的载波跟踪环路依然可以很快收敛，环路收敛时间小于90 ms，频率跟踪误差在5 Hz 以内，相位跟踪误差在0.22 rad 以内，且环路的跟踪性能稳定。而传统的三阶锁频环结合四阶锁相环的跟踪环路，环路收敛时间为1.2 s 左右，频率和相位跟踪误差波动较大，最大可达到20 Hz 和0.5 rad，所以对频率加速信号跟踪时，本文所提出的载波跟踪环路相较于传统环路跟踪性能同样有较大提升。

同样，接下来对两种跟踪环路在不同信噪比下的频率和相位均方误差进行对比。图8 和图9 为环路达到收敛状态时，不同信噪比下的频率和相位的RMSE 曲线，比较了本文提出的载波跟踪环路和传统的三阶锁频环结合四阶锁相环的跟踪环路在不同信噪比下的跟踪性能。在信噪比-20 dB 至-10 dB 的范围内，本文所提出的载波跟踪环路跟踪性能在低信噪比环境下显著优于传统的三阶锁频环结合四阶锁相环的载波跟踪环路。同样，随着信噪比的提升，传统环路的跟踪性能不断接近本文所提出跟踪环路的性能。

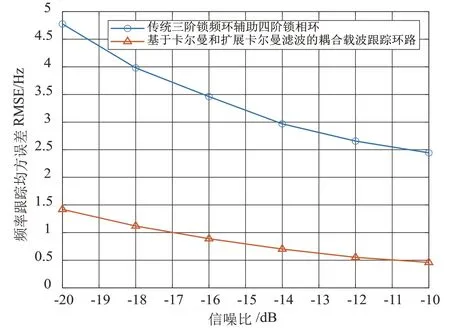
图8 不同信噪比下频率均方根误差

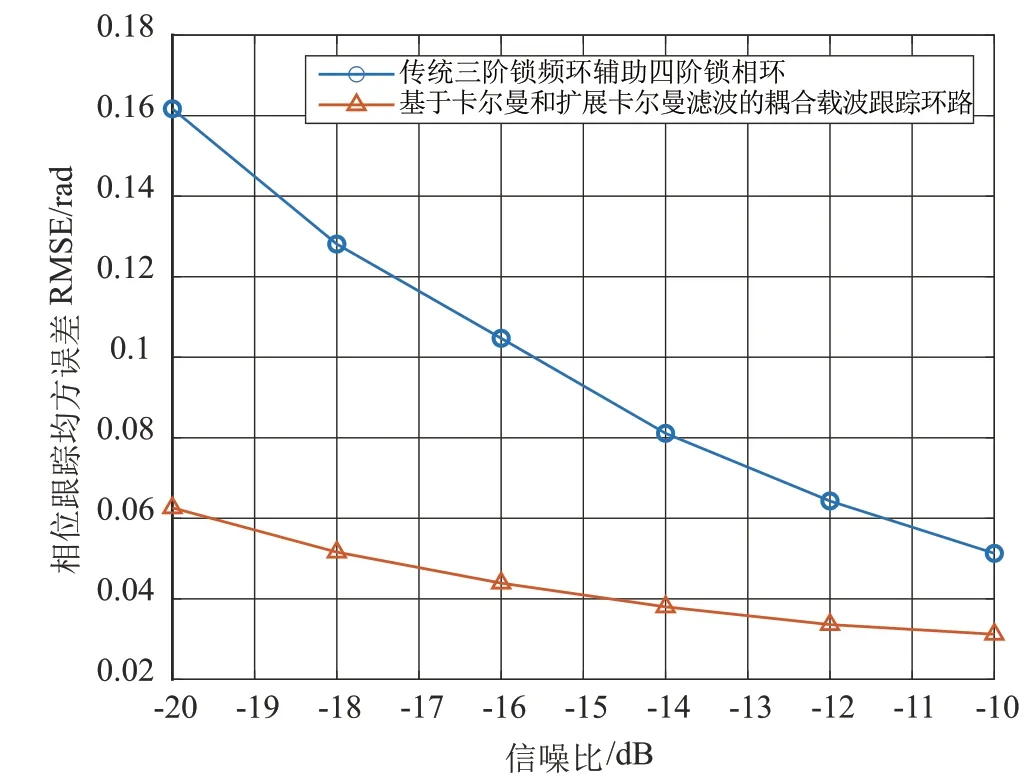
图9 不同信噪比下相位均方根误差

对于JPL 提出的具有代表性的高动态运动模型[21]，即通信终端存在加加速度变化的场景，假设输入信号的多普勒频率为800 Hz，多普勒一阶变化率为10 kHz/s，2～2.5 s 内多普勒二阶变化率为50 Hz/s2，3.5～4 s 内多普勒二阶变化率为-50 Hz/s2，其余时间多普勒二阶变化率为0，仿真时长为5 s。

图10 和图11 展示了1.5～4.5 s 内的频率和相位跟踪误差，出现加加速度变化后，本文所提出的载波跟踪环路在失锁后能够很快的重新恢复收敛，收敛时间小于100 ms，相比之下，传统环路会失锁后环路重新恢复收敛的时间较长，至少需要100 ms。同时，本文所提出的载波跟踪环路的相位跟踪误差波动也相对较小。说明本文提出的载波跟踪环路在应对动态变化时能够达到更好的效果。

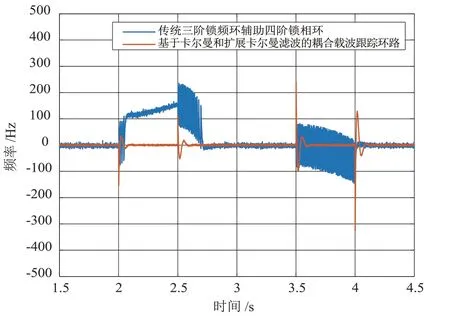
图10 频率跟踪误差

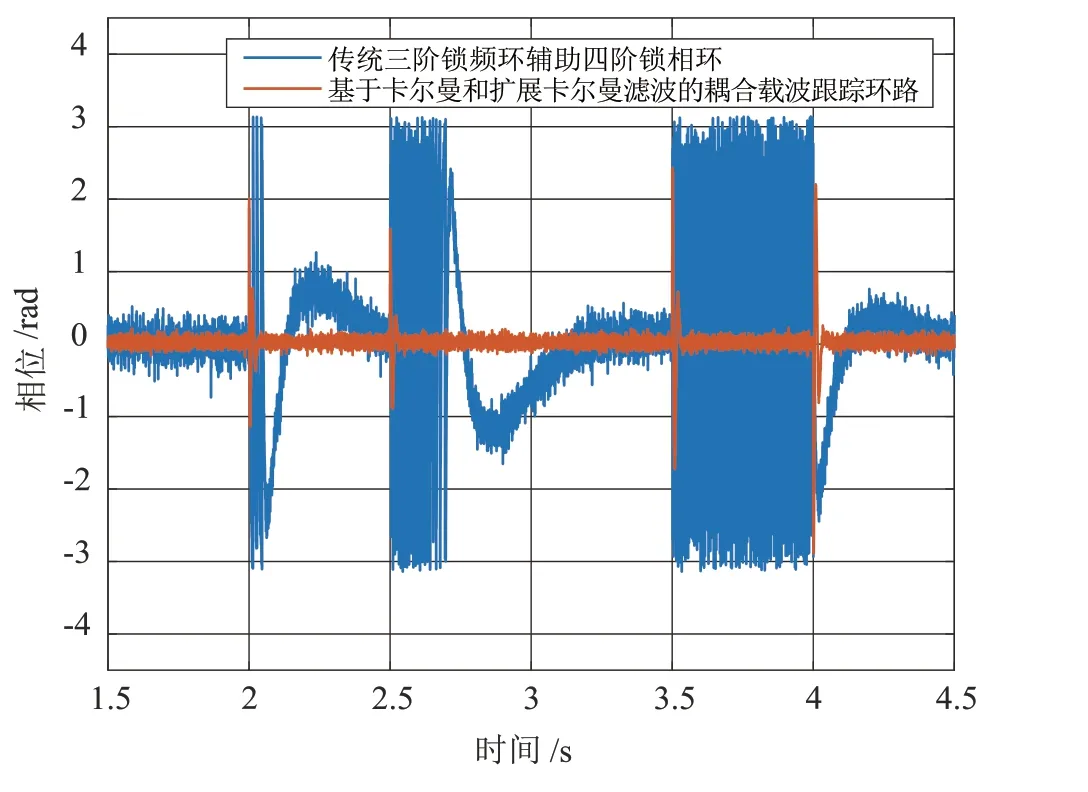
图11 相位跟踪误差

4 结束语

本文提出了一种基于卡尔曼与扩展卡尔曼滤波的耦合载波跟踪环路，将卡尔曼滤波器和扩展卡尔曼滤波器分别与锁频环和锁相环结合起来，实现了低信噪比高动态环境下的载波跟踪。仿真结果表明，该方法在低信噪比高动态环境下对于不同类型的高动态信号均有较好的跟踪性能，即较快的收敛速度和较高的跟踪精度。同时，相较于传统的基于环路滤波器的锁频环结合锁相环的载波跟踪环路，该算法具有更好的跟踪性能。经仿真验证，在信噪比为-20 dB 条件下，该方法跟踪频率斜升信号收敛时间小于60 ms，跟踪频率加速信号收敛时间小于90 ms，对两种信号的频率跟踪残差均小于5 Hz，相位跟踪残差均小于0.25 rad，对于存在加加速度变化的信号，环路重新恢复收敛的时间较短，跟踪性能显著优于传统环路。