面向星地协同网络的联邦边缘学习方法研究*

张雅童，张保庆，孟维晓，陈舒怡

（1.哈尔滨工业大学电子与信息工程学院，黑龙江 哈尔滨 150001；2.北京电子工程总体研究所，北京 100854）

0 引言

传统的地面蜂窝网络虽然近年来发展迅速，但仍进入瓶颈期。地球上的陆地面积大约占全球总面积的29%，海洋的面积则占71%。但地面蜂窝网络也无法将陆地面积全部覆盖，仅覆盖全球陆地面积大约20%的范围。对于海洋的覆盖率则更低，仅约5%。没有地面网络覆盖的区域主要是冰川、沙漠、森林等人员稀少的地区。考虑到这些未覆盖网络的地区面积占比很大且这些区域大多人员稀少，在这些区域建设基站性价比较低。此外，建设在地面的基站当面对突然发生的自然灾害时易遭受损坏，从而无法很好提供应急服务。

卫星网络具有时延低、覆盖范围广等优点。并且，低轨卫星（LEO,Low Earth Orbit）具有覆盖范围广、拓扑密集、组网灵活等优点。各个国家也正在积极促进低轨卫星的研究，比如我国的“天启”、“行云”等。卫星网络和地面网络可以互补协同形成星地协同网络。卫星网络尤其是低轨卫星网络和地面网络互补协同起来形成的星地协同网络具有很大的研究价值和发展前景。

海量设备接入到星地协同网络时会产生大量数据。这些数据极大概率分散在各个用户中，形成一个个数据孤岛。传统的机器学习需要用户将私人数据上传到中心平台，这些数据中极可能包含隐私信息，在机器学习数据上传和下发的过程中，这些隐私存在泄露的可能。联邦学习（FL,Federated Learning）作为分布式学习，在2016 年由谷歌团队首次提出[1]，可以让参与训练的各个用户在不共享数据的情况下实现协作训练，从而可以解决在星地协同网络下分析大量数据时出现的数据孤岛和数据隐私问题。联邦学习的应用场景很广泛，比如McMahan 等人[2]提出了一种联邦均衡（FedAvg,Federated Averaging）算法，用于优化Google 的Gboard[3]手机输入法的一个模型预测的准确性。Brisimi 等人[4]通过点对点协作提出了一种新的预测模型联邦学习框架，这种模型可以准确预测与心脏相关的住院情况。但传统的联邦学习通常为多个用户进行本地训练，一个聚合设备负责全局的聚合，面对网络中大量的用户时会出现通信效率较低的问题。在边缘计算（EC,Edge Computing）基础上提出联邦边缘学习（FEL,Federated Edge Learning）。联邦边缘学习进行边缘聚合后，将模型再传到远端云服务器进行全局聚合。例如，文献[5]提出了一种分层的联邦边缘学习算法，多个用户在本地进行本地训练后，将其生成的模型上传到多个边缘设备中进行边缘聚合，再将边缘模型上传给云端获得全局模型。边缘计算靠近数据源，可以为本地设备的大量数据提供处理、存储资源和计算[6]等帮助。当多个设备联合进行机器学习等协同训练时，通过将模型靠近本地设备来减小传输时延[7]。边缘计算目前在智能家居、智能城市和智能医疗等一些和人们生活相近的领域有着极大地应用场景[8]。边缘聚合可以减小传统联邦学习的通信成本。面对星地协同网络，可以将轨道上的多颗卫星作为边缘聚合设备进行联邦边缘学习。一般的联邦边缘学习中全局聚合设备为云服务器。考虑到低轨卫星轨道高度较低、且会围绕地球进行快速运动，将低轨卫星作为边缘聚合设备时，易出现卫星和云服务器不可见的情况。同时，在星地协同网络下进行联邦边缘学习，除模型精度外，还需要确保在协同网络中实现联邦边缘学习时的全过程时延不能过高，因此需要对传统联邦边缘学习进行改进。星地协同网络下的联邦边缘学习的研究目前还比较少。目前主要是对星地协同网络下的边缘计算进行研究，例如，文献[10]提出卫星作为边缘设备实现边缘计算的概念，通过引入动态网络虚拟化技术来实现网络资源的整合。同时，在系统中设计了协同计算的卸载方案，最终实现并行计算且减小时延。文献[11]对卫星实现边缘计算进行了建模分析。对不同轨道、不同卫星卸载速率下的传输延迟以及上下行链路的传输延迟进行了分析和研究。也有一些学者对星地协同网络下的联邦学习进行了研究。文献[12]以多颗卫星和一个地面站为背景设计异步联邦学习，通过判断卫星所处的集合来判断对其的操作进而减小训练的时延。文献[13]在文献[12]的基础上提出一种判断程序，通过比较模型的训练时延和卫星和地面站之间的可见时延，进一步减小时延。文献[14]在多颗卫星和一个地面站之间提出一个高效的联邦学习框架，对卫星的空闲时延和局部模型陈旧两方面进行联合优化。文献[15]主要研究星地协同网络下的数据攻击问题，以多个卫星以及多个用户设备为背景，使用多个卫星负责模型的聚合，研究不同的数据攻击对其所提出的联邦边缘学习算法的影响。但是这些研究主要是将卫星作为本地训练设备且采用一个地面站作为聚合设备，和本文的场景并不匹配。

因此，本文面向星地协同网络，提出一种适合于星地协同网络的联邦边缘学习算法。算法可以对在星地协同网络中海量设备产生的大量数据进行分析处理时出现的隐私信息泄露和数据孤岛问题进行解决，并且可以使协同网络中进行联邦边缘学习算法的全过程时延较低，模型测试精度较高。

1 分层聚合模型

考虑在星地协同网络场景下，利用底层地面设备进行本地训练，上层低轨卫星进行边缘聚合，并利用轨道卫星的环状结构实现全局聚合。具体星地协同网络下分层聚合训练场景如图1 所示：

图1 星地协同网络下实现联邦边缘学习的分层聚合场景

考虑到低轨卫星和地面设备之间的可见时间段较短，采取卫星和地面设备可见时去交换联邦边缘学习的参数的方法会导致联邦边缘学习算法的全过程时延很高。考虑到卫星运动具有周期性和可被预测性的特点，可以利用覆盖域模型[16]将卫星和本地设备之间的动态星地链路转化为静态星地链路。目前，卫星天线的工作模式主要有卫星固定足印模式以及地球固定足印模型[17]，本文假设卫星的天线工作在地球足印模式。覆盖域模型可以将地球表面区域按照卫星数划分为若干规则的区域，并给每个划分好的区域分配一个逻辑地址。逻辑地址包含着地理信息，每个区域称为一个逻辑卫星位置。

需要说明的是，在星地协同网络中进行联邦边缘学习，实际上本地设备是上传给本地训练结束时刻其对应的逻辑卫星位置在当前时刻的卫星，并从该卫星接收卫星的加权平均参数再次进行本地训练。之后，由其所对应的逻辑卫星位置在当前时刻的卫星来下发全局模型。

假设在协同网络中有位于同一轨道的Ns颗低轨卫星，有N个本地设备。每颗卫星负责Ng个地面设备的边缘聚合。Nk表示卫星k所负责的本地设备的集合，即。

算法中所有的地面设备可以表示为：

集合Nk中的第i个本地设备的数据集为Dk,i，则第Nk组的数据集为：

分层聚合主要是分为将卫星作为边缘设备进行边缘聚合以及利用卫星轨道环状结构实现全局聚合两部分，分别介绍如下。

卫星作为边缘设备进行边缘聚合指的是卫星作为边缘设备对其负责的地面设备上的参数进行加权平均。每个本地设备首先进行多轮本地训练。在第t轮本地训练时，卫星k负责的地面设备在本地训练阶段的参数是。本地训练采取随机梯度下降的方式来更新参数，即式(4)，其中η表示学习率。

当进行τ1轮本地训练，即时，每颗卫星进行边缘聚合。具体是从该卫星在当前时刻所对应的逻辑卫星位置相关联的本地设备上收集相应的参数，进行参数的加权平均得到，即式(5)：

当进行τ2轮卫星边缘聚合后，即tmodτ1τ2=0 时，进行一次全局聚合。面对星地协同网络，考虑到负责参数加权平均的卫星位于同一环状轨道。可以利用这种环状结构实现全局聚合。

当同一环状轨道上的卫星进行全局聚合时，一般是将一颗卫星作为主卫星来实现参数的全局聚合。但这种情况会导致冗余的卫星多跳而增加算法的时延。考虑到同一轨道的环状结构，卫星全局聚合利用Ring-Allreduce 算法[18]。算法仅需卫星进行单向环形传输来实现联邦边缘学习参数的传递进而实现全局聚合，具体主要分为两步：

（1）Scatter-reduce：假设共有n颗卫星。首先给每个卫星进行编号并指定其左邻居和右邻居。然后将每个卫星得到的模型参数根据数据集进行加权，即得到加权模型参数。然后，将每颗卫星的加权模型参数都均等划分成n个数据块。在每次迭代中，每颗卫星都会将自己的其中一个数据块发送给右邻居，并从左邻居接收其发送的一个数据块。每颗卫星需要将接受来的数据块和自己对应编号的数据块进行求和。在每次迭代中，发送和接收的数据块不同。经过n-1 次迭代后，每颗卫星都将包含一个具有所有卫星的对应编号的数据块之和的数据块。以n=5 为例考虑五颗卫星的场景，首先将每颗卫星的加权模型参数都按照卫星的个数均等划分为五个数据块，即卫星Si的加权平均参数，将加权平均参数划分为五个数据块。经过4 次Scatter-reduce 算法迭代后，每颗卫星所包含的数据块具体如图2 所示。

图2 Scatter-reduce步骤进行4次迭代后包含数据块图

（2）Allgather：当完成Scatter-reduce 后，进行Allgather。在Allgater 的第一次迭代中，第n颗卫星首先发送其第n+1个数据块并接收左邻居发来的其第n个数据块。和scatterreduce 不同的地方在于scatter-reduce 部分，当卫星接收到左邻居发出的数据块后需要进行和其对应编号的数据块加和操作，然后将加和结果替代当前编号的数据块。而Allgather 则是直接将接收到的数据块替代原来对应编号的数据块，而不进行加和操作。在未来的迭代中第n颗卫星总是发送它刚收到的数据块。在进行了n-1 次迭代后，每颗卫星都具有所有卫星的加权模型参数。以五颗卫星为例，第四次迭代后，卫星所包含的数据块如图3 所示。其中，任何一个卫星的数据块总和等于。

图3 Allgather步骤进行4次迭代后数据块图

综上，对于轨道面Ns颗卫星，每颗卫星需要执行Ns-1次Scatter-reduce 迭代，再执行Ns-1 次Allgather 迭代。第一颗卫星的数据块之和即为全局参数，由此就可以实现全局聚合。之后，每颗卫星将得到新的全局参数发送给其关联的地面设备作为新的本地参数来进行新一轮的本地训练。

综上所述，算法的主要过程可以总结为式(7)：

2 用户关联策略

除模型精度外，在星地协同网络中进行联邦边缘学习时还需要保证全过程的时延不能过高。全过程时延主要由通信时延、计算时延以及星间全局聚合所需的时延三部分组成，即。进行一轮联邦边缘学习所需通信时延为：

其中，式(10) 中M是模型参数的大小。M/N表示链路的接收端信噪比。BXY为链路带宽。式(11) 中LXY为端到端的实际距离。VXY为传输介质中的传输速率。

计算时延包括本地设备的本地训练时延以及卫星进行边缘聚合的时延，即式(12)。Ttrain为本地训练时延，如式(13)，其中FLOPs为模型的浮点运算次数，用来衡量模型的复杂度。FLOPs是地面设备每秒的浮点运算次数，用来衡量硬件的性能，是每轮本地训练的样本数目。是卫星聚合时延，即式(14)，其中表示接收到的模型数目，FLOPs是卫星每秒的浮点运算次数，M是模型参数的大小。

星间全局聚合利用Ring-Allreduce 算法。假设卫星的数量是Ns颗。每颗卫星需要执行共计次迭代，如式(15)：

模型精度方面，在τ1和τ2固定的情况下，当为每个聚合设备尽可能分配具有不同类别样本的本地设备时，模型测试精度较高。对星地协同网络，同一卫星负责进行边缘聚合的本地设备之间的数据集相异度越大，模型测试精度越高。

通过对全过程时延和模型精度的分析，提出一种基于地理位置和数据集相异度的用户关联策略。基于此策略的联邦边缘学习算法可以实现协同网络中全过程时延和模型精度两个参数之间的联合优化。在提出本文所使用的用户关联策略之前，首先考虑两种极端的用户关联策略，分别定义为完全基于地理位置的用户关联策略和完全基于数据集相异度的用户关联策略。完全基于地理位置的用户关联策略指的是将每个逻辑卫星位置上的地面设备都对应到本地训练结束时其所在的逻辑卫星位置在该时刻对应的卫星。完全基于数据集相异度的用户关联策略是给每个卫星都分配具有尽可能不同的数据集分布的本地设备。但上述两种极端情况仅可以减小时延或提高测试精度。因此，基于上述两种极端策略提出基于地理位置和数据集相异度的用户关联策略。

基于地理位置和数据集相异度的用户关联策略首先设计在地理位置上的划分。将所有的逻辑卫星位置均分成一些不重叠的分区，每个分区包含连续的Nleo个逻辑卫星位置。根据Nleo个逻辑卫星位置的分区，本地设备可以划分成Ns/Nleo个区域。在对逻辑卫星位置和本地设备进行分区后，使用K-means 算法[19]对每个分区内的本地设备根据它们之间的数据集的相异度进行本地设备的划分，将由此得到的每个本地设备的集合称为类似簇。根据K-means 算法可以使每个类似簇中的本地设备之间的数据集的相异度很小。然后，设置Nleo个空对应簇，从每个类似簇中随机选取一个本地设备加入对应簇中。最终，每个分区都可以得到Nleo个对应簇，并且每个簇中本地设备的数据集之间相异度有较大差异。然后采用LAPJV 算法[20]将Nleo个对应簇映射到Nleo个逻辑卫星位置，使Nss最小，从而可以进一步减小算法全过程时延。

LAPJV 算法具体为先求解出每个对应簇中的地面设备对应到分区内的某个逻辑卫星位置时所需卫星总跳数。以同一轨道面上的卫星数为20 颗，地面设备设置为200个为例进行LAPJV 算法的应用说明。首先假设设备的编号为XZ，，所对应的逻辑卫星位置为。考虑到同一轨道的卫星的环状结构，需要比较卫星左跳传输和右跳传输转发之间的跳数的大小，并取较小值，则该设备的卫星多跳M可以表示为：

当计算出每个对应簇的总卫星跳数，即在簇内每个本地设备对应到某逻辑卫星位置区域的所需的跳数之和后，进行LAPJV 算法来求出映射关系使得全部簇内所有本地设备所需的总卫星跳数最小。LAPJV 算法通过输入一个方阵，最终来获得一列最佳的分配数值，对应到星地协同网络下的用户关联策略中，以第一个分区为例，假设一个分区内的对应簇为，逻辑卫星位置为，则每个簇对应每个逻辑卫星位置的总跳数可以表示为，则方阵可以表示如下：

当使用LAPJV 算法时，可以得到一条从第一行不后退走到最后一行的路径，并且路径上的矩阵数值之和最小。因此，通过LAPJV 算法可以得到使总跳数最小的逻辑卫星位置和对应簇之间的映射关系。综上所述，基于地理位置和数据集相异度的用户关联策略可以实现精度和时延的联合优化，下图为以Nleo=2、Ns=4 为例的逻辑卫星位置和本地设备之间的用户关联策略。最终，包含用户关联策略的联邦边缘学习算法可以实现时延和模型精度的联合优化。需要说明的是，目前这种关联策略需要用户均匀的分布在每个逻辑卫星位置里面，且卫星天线为地球固定足印模式的理想场景，后续会继续对策略进行深入研究和修改以适配更为实际的场景。

图4 为用户关联策略案例。

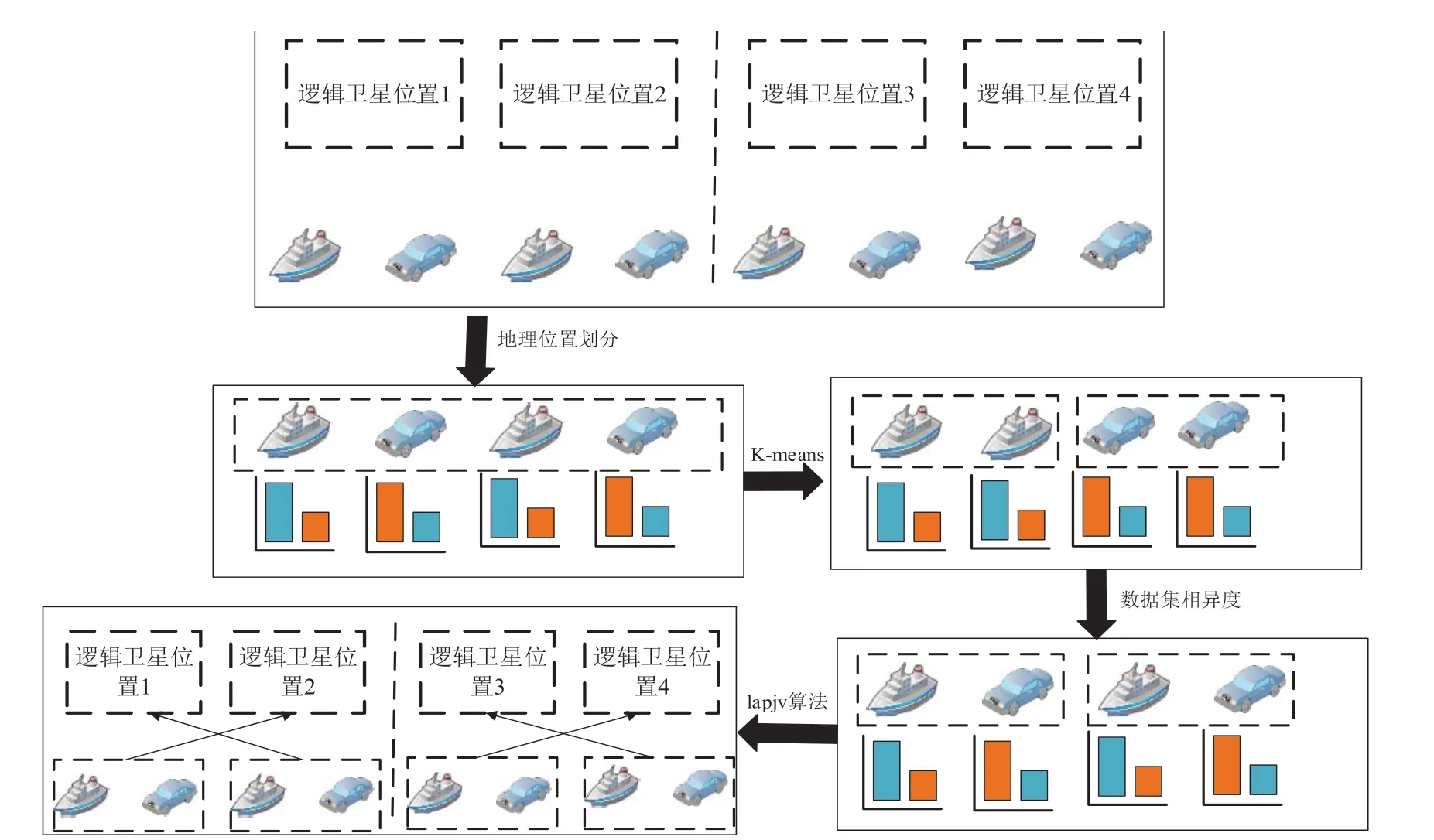
图4 用户关联策略案例

3 仿真分析

在星地协同网络中进行联邦边缘学习算法的仿真参数具体设置如表1 所示。仿真过程中使用CNN 卷积神经网络，使用MNIST 数据集进行星地协同网络下的联邦边缘学习算法的仿真。本地设备的非独立同分布设计采用狄利克雷分布。对于星地协同网络的上行链路，地面设备的发射功率设置为2.5 W，带宽为1 MHz。用户天线增益为0 dB，卫星天线的增益为53 dB，额外损耗为5 dB，自由空间损耗为186.6 dB。下行链路的设计中，卫星发射功率设置为10 W，自由空间损耗为183.0 dB。由于星间链路设置为激光链路，带宽无限大，卫星激光通信的波长选择多使用1 550 nm，比如美国的LCRD[21]。卫星轨道高度设为1 690 km。

表1 仿真参数表

将完全基于地理位置和完全基于数据集相异度的用户关联策略作为对照组，进行包含基于地理位置和数据集相异度的用户关联策略的联邦边缘学习算法仿真。

图5为三种用户关联策略方式下联邦边缘学习模型精度。通过仿真可以发现完全基于数据集之间相异度的方式下的联邦边缘学习的精度最高，用户关联策略次之，完全基于地理位置下的精度最低。这是因为在完全基于数据集之间相异度的方式中，每颗卫星负责聚合的本地设备之间的数据集相异度都是尽可能不同的，从而设备之间更加趋于非独立同分布，模型的泛化能力更强，训练后的精度更高。而完全基于地理位置的划分主要保证时延。但是地面设备的数据集分布类似，导致模型的精度最低。用户关联策略则是在划分区域的基础上再根据数据集之间相异度来选择地面设备，精度处于两种极端情况之间。同时还可以发现完全基于数据集之间相异度的情况下的精度曲线在300 轮训练中的趋势是先上升后下降。这是因为模型学习到一定程度后，接着训练会使其趋于训练细枝末节的部分。这会使得在测试集上的表现变差。

图5 三种用户关联策略方式下联邦边缘学习模型精度

在时延方面，分别计算当τ1=60、τ2=1；τ1=15、τ2=4；τ1=6、τ2=10 时三种用户关联策略方式下联邦边缘学习算法的一轮训练时延。

图6 为不同用户关联策略方式下的改变联邦边缘学习参数下的时延。

图6 不同用户关联策略方式下的改变联邦边缘学习参数下的时延

当参数τ1和τ2固定时，时延结果从大到小为完全基于地理位置的用户关联策略方式下的联邦边缘学习算法、所提出的包含用户关联策略的联邦边缘学习算法、完全基于数据集之间相异度的用户关联策略方式下的联邦边缘学习算法。这主要是因为完全基于地理位置的用户关联策略方式是直接将设备分配给其所在区域的逻辑卫星位置所对应的卫星，并不需要中继卫星进行转发。而完全基于数据集之间相异度的用户关联策略方式是尽量给每个位置分配数据集相异度很大的地面设备，脱离了地理位置的限制，使得中继卫星进行转发的次数极大。用户关联策略则是在地理位置限制的基础上根据数据集相异度进行划分，时延在两种极端方式之间。

通过时延和精度的分析可以发现包含用户关联策略的联邦边缘学习算法可以实现时延和精度之间的联合优化。以τ1=6、τ2=10 为例，本文提出的包含用户关联策略的联邦边缘学习算法相比完全基于地理位置的用户关联策略方式下的算法的模型精度提高6.4%，时延增加185%。本文提出的包含用户关联策略的联邦边缘学习算法相比完全基于数据集之间相异度的用户关联策略方式，模型精度下降3.5%，时延减少134%。

4 结束语

本文提出一种适用于星地协同网络且可以实现时延和模型精度联合优化的联邦边缘学习算法。算法主要包括利用卫星进行边缘聚合、基于卫星轨道的环状结构进行全局聚合的分层聚合方式和基于地理位置和数据集相异度的用户关联策略。MNIST 数据集仿真结果表明，这种联邦边缘学习算法不仅可以有较高的模型精度，且能计算出全过程所耗费的时延，并实现时延和模型精度之间的联合优化。