基于主成分回归模型的建筑人工单价预测研究

韦雅男

（鉴甄检测技术(苏州)有限公司，江苏 苏州 215000）

0 引言

随着我国社会经济水平的不断发展，社会生产力水平也在不断地提高，给我国建筑行业的快速健康发展带来了巨大机遇，国内涌现出一大批规模大、技术强的建筑施工企业。但随着建筑项目用工量的逐年增加，工作环境差、用工时间长、危险性大等问题逐步暴露出来，建筑从业人数出现了较大幅度的下降，建筑劳务市场供求关系日趋紧张。近年来，我国建筑行业人工单价水平不断提高，据相关数据统计[1]，2010年～2018年间我国人工成本平均涨幅达到8%～20%；近些年逐步放缓至3%～5%区间；建筑工程直接成本中人工成本占比已达到35%左右，但与欧美等国家50%左右的占比相比仍有较大涨幅空间。因此，研究建筑工程直接成本中人工成本的构成，预测市场人工成本的发展趋势，对建设工程承包过程中合理有效地确定和控制项目人工成本具有重要意义。

1 定额人工单价特征指标选取与影响因素

1.1 特征指标选取原则

定额人工单价是指在国家规定的工作日制度下，工人在正常施工条件下施工一个工作日的全部人工费用[2]，市场人工单价是施工企业依据项目所在地的劳务用工工资所支付的工资报酬[3]。定额人工单价与市场人工单价会因为工作时间、内容、效率、工种的差异出现较大的差距[4]。

在多元线性回归分析模型中，因变量受到自变量的影响，但是每个自变量对因变量的影响程度是不同的，因此建立多元线性回归模型需要准确合理地选择与因变量有一定关系的特征指标变量，且这些特征指标变量的数据获取应简单方便。将多元线性回归模型应用于定额人工单价的预测中，将定额人工单价作为因变量，将影响定额人工单价的因素作为自变量，结合市场经济发展数据并参考文献资料，准确合理地选取影响定额人工单价的特征指标，特征指标应能体现市场经济发展的趋势，还应具备可量化且易获取的特征。

1.2 定额人工单价的影响因素

一般而言，定额人工单价作为建设项目投资的参考，是特定时期特定区域内的综合水平，虽然各级政府部门确定了定额人工单价的发放标准，但对施工企业内部工人工资的发放并未做约束[5]。具体而言，定额人工单价的主要影响因素与某一时期的劳动力市场供求关系、社会经济发展水平、物价增速、人口结构及就业偏好等因素有关[6]，因此初步选取的特征指标变量包括建筑产业总产值、区域最低工资标准、人均GDP、区域消费者价格指数、全国建筑工程产值及区域建筑工程产值等具备量化且易获取的指标。

2 主成分分析法

2.1 主成分分析法理论基础

主成分分析法是在1901年由英国生物统计学家卡尔皮尔逊提出，是一种多元统计分析中解决降维问题的有效方法，其主要研究众多自变量之间的内在关系并进行降维处理的基本思路，在一定程度上简化了指标体系，使结果更为客观，其数学模型表达式为：

式中：

X1～Xn——n个自变量；

F1～Fm——m个主成分；

ε1～εm——实际值与预测值间的误差值。

式（1）可简化表述为：

式中：

A——主成分中的成分系数矩阵；

F——主成分矩阵；

ε——误差矩阵。

2.2 主成分分析法实施步骤

2.2.1 特征指标变量标准化

根据因变量特征选取的具有代表性的特征指标变量由于在数量级及量纲上的差异，无法进行直接比较且不具备一定的可比性，因此，在使用主成分分析法前，应对原始变量进行标准化处理，以消除特征指标变量在数量级及量纲上的差异，标准化公式如下：

式中：

ZXi——标准化后的特征指标变量；

Xi——标准化前的特征指标变量；

E(Xi)——特征指标变量Xi的平均值；

Var(Xi)——特征指标变量Xi的平方差。

2.2.2 适用性检验

为复核经标准化处理后的特征指标变量是否满足主成分分析的条件与要求，应对各因子进行适用性检验。主成分因素分析法适用性检验一般可采用KMO检验法，KMO法通过比较变量之间的相关系数和偏相关系数来检验统计量的适用性，计算公式如下：

式中：

rij——特征指标变量Xi和Xj之间的相关系数；

pij——特征指标变量Xi和Xj之间的偏相关系数。

KOM计算结果的判断标准为：KOM=(0.9,1]时表示样本量合适，适用性好；KOM=(0.8,0.9]时表示样本量基本合适，适用性较好；KOM=(0.7,0.8]时表示样本数量一般，适用性一般；KOM=(0.6,0.7]时表示样本数量较少，适用性不太合适；KOM=(0,0.6]时表示样本数量偏少，适用性不合适，需要扩大样本数量重新进行适用性检验。

2.2.3 提取主成分

为简化计算，通过对因变量的特征分析，在众多特征指标变量中提取部分可以反映变量信息的主要因素，根据主因素分析法的理论计算公式（1），从公式（1）中提取前K个主成分并以矩阵的形式表述为：

式中：

a11…ank——特征指标变量在对应主成分上的权重值；

λ1…λn——特征值；

u11…unk——协方差矩阵特征值所对应的特征向量。

2.2.4 主成分因子的计算

采用原始向量的线性组合来表述提取出来的主成分因子，即：

式中：

Xn——标准化后的特征指标变量；

βjn——主成分F在特征指标变量Xi上的得分系数。

3 工程应用实例

3.1 数据样本库建立

采用回归模型进行分析前需要收集一定数量的历史样本数据，且当收集的历史样本数据越多，回归方程的计算精度就会越高，一般精度要求下的样本数量是影响因素指标的3～5倍。本文通过中国统计年鉴、造价信息网及城市当地统计年鉴为数据库基础，收集选取了苏州市2015～2020年度各季度具有普遍性及规律性的特征指标用于数据研究，用获取的24组数据作为每个影响因子的数据基础，创建样本库，24组样本中的部分样本数据见表1所示。

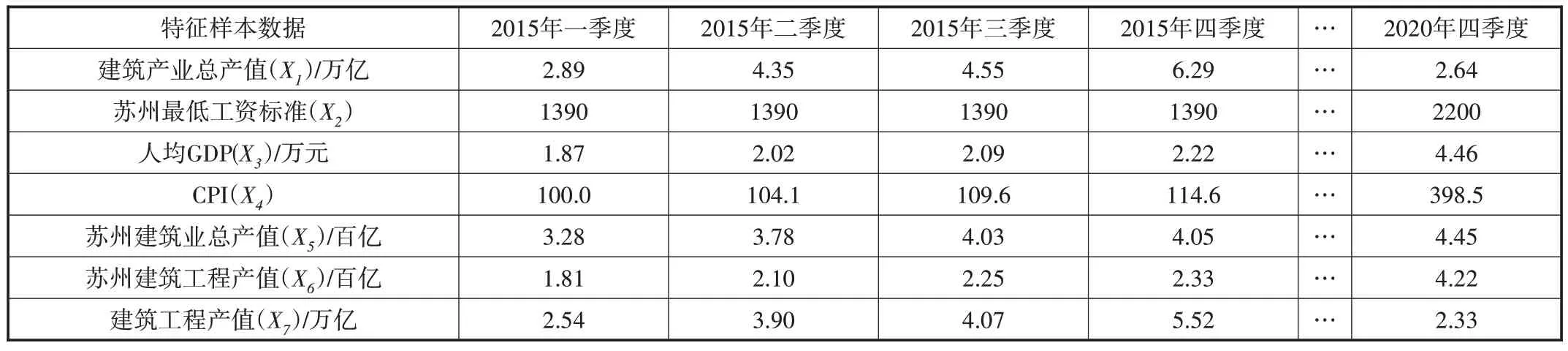
表1 部分样本数据（苏州市）

3.2 数据初步回归及共线性诊断

为判断指标间的共线性关系，采用SPSS软件对各样本数据进行共线性诊断，并根据诊断结果统计分析各变量两两间的相关关系，验证模型中的自变量与因变量是否存在较好的相关性，如表2所示。

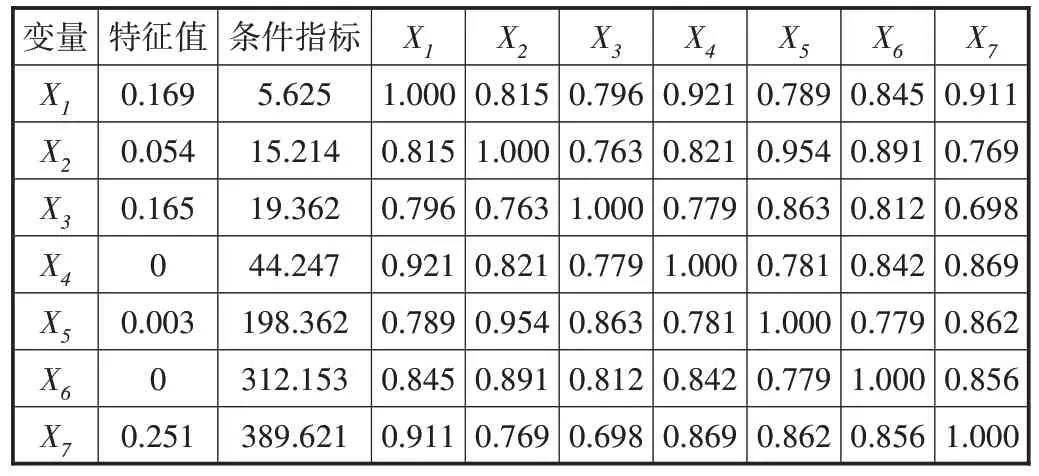
表2 特征样本数据共线性诊断结果及相关系数表

根据诊断结果可知，特征样本数据中有2个变量的特征值为0，其余5个变量特征值接近0，6个变量的条件指标>10，证明各个变量间存在两两的多重共线性关系，且各指标数据间的相关系数均处于0～1之间，本文收集的数据样本符合主成分回归模型的数据精度的要求。根据公式（4），采用KMO法对各变量因子进行适用性检验，样本数据的KMO 检验值为0.815，根据KMO 检验法理论，当KOM=(0.8,0.9]时表示样本量基本合适，适用性较好，本文所收集的样本数据适合进行主成分因子分析。采用SPSS软件计算得出特征样本数据的成分系数矩阵如表3所示。

表3 成分得分系数

根据本文公式（6），获得主成分因子表达式为：

将主成分因子F1和F2作为自变量，再次对因变量进行多元线性回归分析，计算得到的回归方程系数分析表如表4所示。

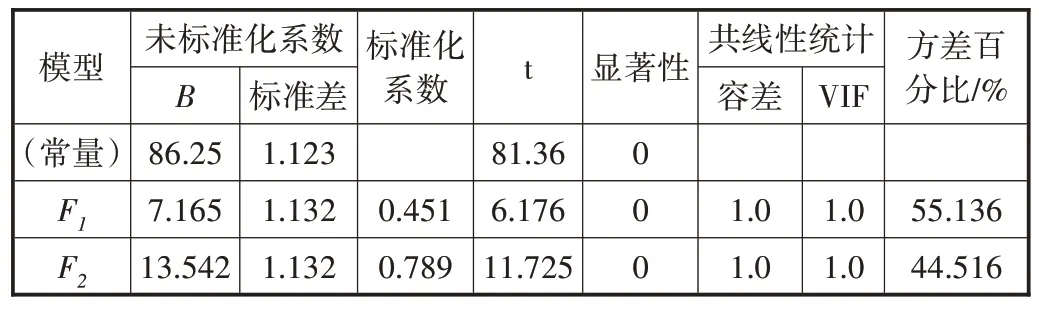
表4 多元线性回归方程系数分析表

结合公式（7）并根据表4的多元线性回归方程系数，建立市场人工单价的多因素主成分回归模型表达式为：

式中：

F——市场人工单价预测值；

F1和F2——与特征指标变量相关的成分因子，按式（7）计算。

为验证该模型的拟合程度，可采用SPSS软件计算模型的显著性，经计算，F检验变化量为89.25，概率值水平<0.05，证明该模型的回归性较好。

3.3 主成分分析法的应用

将苏州市2021年前3季度的特征指标的相关数据代入主成分分析模型中，并将计算得出的预测值与实际值进行对比分析，最终的预测值及实际值计算结果如表5所示。

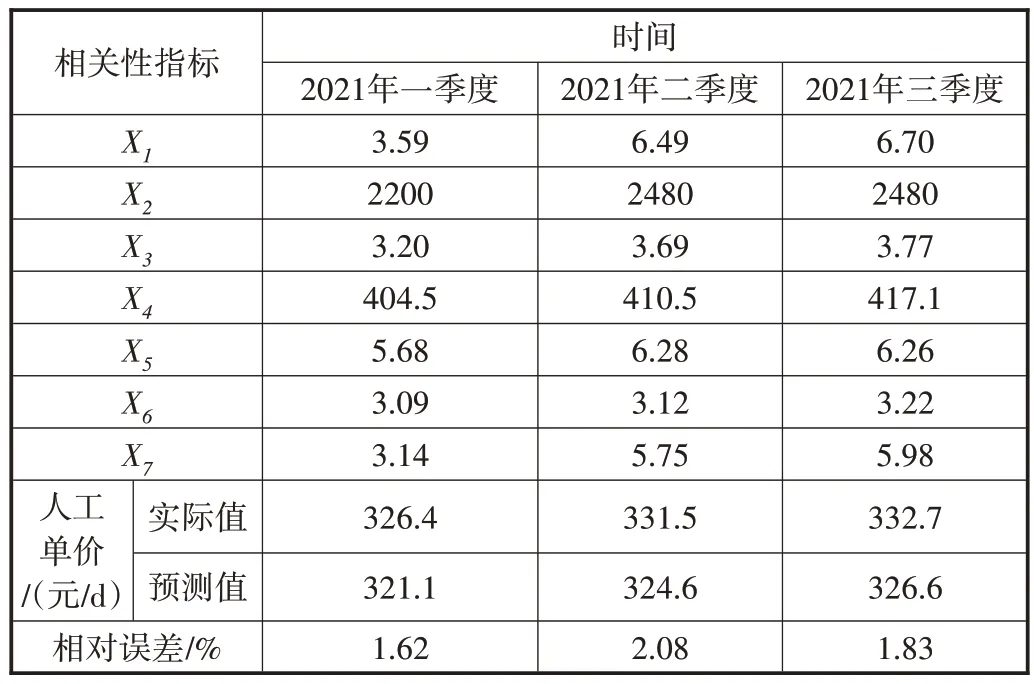
表5 苏州市2021年前3季度市场人工单价的预测值及实际值

根据表5的计算结果可知，2021年度1～3季度人工单价的实际值与预测值之间的相对误差精度均<3%，证明本文所建立的回归分析预测模型的可靠性较好，可以满足建筑产业市场人工单价的预测分析。

4 结束语

本文在分析定额人工单价主要影响因素的基础上，确定影响指标的选取原则。基于主成分分析法，采用SPSS软件对选取的指标数据进行初步回归分析及多重共线性诊断，并引入主成分因子分析法消除其共线性问题，建立主成分因子回归分析模型。根据2021年前三季度特征指标的样本数据，对2021年前三季度建筑市场人工单价进行预测，并与实际值相比较，结果表明，预测值与实际值相对误差<3%，模型精度满足要求，该主成分回归预测模型可用于建筑行业市场劳务单价的预测工作。