过渡态理论对Arrhenius公式的诠释<br/>——以硝酸异丙酯与自由基反应为例

过渡态理论对Arrhenius公式的诠释
——以硝酸异丙酯与自由基反应为例

2024-03-04孙翠红许保恩刘迎杨静吕立强

大学化学 2024年1期

孙翠红，许保恩，刘迎，杨静，吕立强

石家庄学院化工学院，石家庄 050035

瑞典化学家Arrhenius根据实验从宏观的角度总结出了化学反应的动力学基本规律——Arrhenius公式(1)，揭示了反应的速率常数与温度的依赖关系。

他认为，反应的速率常数k与温度T的关系取决于反应的活化能Ea和指前因子A。人们先后运用碰撞理论、过渡态理论、单分子反应的林德曼理论从微观的角度对Arrhenius公式进行解释。高校化学教师围绕Arrhenius公式的形式以及活化能的概念进行了讨论[1–4]。罗渝然等[1]介绍了国际纯粹与应用化学联合会(IUPAC，1996)推荐的活化能定义，并以基元反应D + H2为例，强调了活化能与诸多相似物理量的区别；黄图伦[3]在介绍Arrhenius速率方程基础上，从碰撞理论、过渡态理论和托尔曼统计等视角诠释了活化能概念，他认为，对于包含多步反应过程的复杂反应体系，不能简单地仅以活化能大小作依据判断反应的反应速率大小。盛卫群[4]对Arrhenius公式几种数学表示形式及其意义进行讨论，并对活化能的定义和本质进行详细阐述。鉴于这部分内容的理论性强，不易被学生理解和掌握，本文基于笔者的科研论文“硝酸异丙酯与Cl原子、OH和NO3自由基反应的机理及动力学”[5]，针对硝酸异丙酯(IPN)与Cl原子、OH和NO3自由基反应的机理相似但能垒不同，直观形象地讨论并展示了反应速率常数随温度变化情况及其与能垒的关系。

1 从Arrhenius公式看反应速率常数k与温度T及活化能Ea的关系

现有物理化学教材对温度与活化能的关系均有不同程度的讨论[6]。

对式(1)取对数，得到

若假定A与T无关，则得到微分形式

对于具有不同活化能的两个反应，分别设为反应1和反应2，则有

两式相减，得

若Ea,1＞Ea,2，当温度升高时，k1/k2的比值增加，即k1随温度的增加倍数大于k2的增加倍数。

根据式(2)，以lnk对1/T作图，可得一直线，直线的斜率是Ea/R。在一定温度范围内，把Ea看做是与温度无关的常数，则Ea越大，斜率(绝对值)就越大。分析可知，反应速率常数k与温度T的关系如下[6]：

(1) 对于一个给定的反应，在低温范围内反应速率随温度的变化更敏感。

(2) 对于活化能不同的反应，当温度增加时，Ea大的反应，速率常数增加的倍数比Ea小的反应增加的倍数大。

2 过渡态理论中反应能垒E0与Arrhenius公式中活化能Ea的比较

过渡态理论：

式中，kB为玻尔兹曼常数，h为普朗克常数，T为温度，q#和qB分别为反应中过渡态和反应物的配分函数，R为摩尔气体常数，E0为量子能垒。即在经典能垒的基础上，分别对反应物和活化络合物做零点能修正[1]，为活化络合物与反应物的零点能之差，即0 K时的活化能[7]。需要说明的是，活化能Ea为可测的宏观量、统计量，而量子能垒是微观的、分子水平的量，不可观测。但是，微观量子能量E0是实验活化能Ea存在的实质，可以通过过渡态理论中量子能垒E0的大小，来定量解释反应速率常数k与温度T之间的关系。

3 硝酸异丙酯与Cl原子、OH和NO3自由基反应的势能面及动力学特征

3.1 硝酸异丙酯与Cl原子、OH和NO3自由基反应的势能剖面图

“硝酸异丙酯与Cl原子、OH和NO3自由基反应的机理及动力学”[5]一文，采用CCSD(T)//M06-2X/6-311++G(d,p)方法，结合传统过渡态理论，研究了硝酸异丙酯与Cl原子、OH及NO3自由基的反应机理和动力学。结果表明，Cl原子、OH和NO3自由基可提取硝酸异丙酯中叔碳的α-H原子或甲基的β-H原子，室温下，以自由基提取α-H原子为主反应通道。本文以Cl原子、OH和NO3自由基提取IPN中的α-H (主反应通道)为研究对象进行讨论。

在IPN + Cl、IPN + OH、IPN + NO3三个反应中，Cl原子、OH和NO3自由基分别与IPN形成氢键复合物COM―Cl、COM―OH和COM―NO3，之后Cl原子、OH和NO3自由基分别靠近IPN中的α-H原子，同时C―H键拉长，生成过渡态TS―Cl、TS―OH和TS―NO3，最终C―H键断裂，分别生成产物HCl、H2O、HNO3和(CH3)2CONO2自由基，该自由基很不稳定，随即分解为丙酮和NO2。M06-2X/6-311++G(d,p)方法计算所得各反应体系α-H提取的反应复合物、过渡态构型如图1所示[5]。

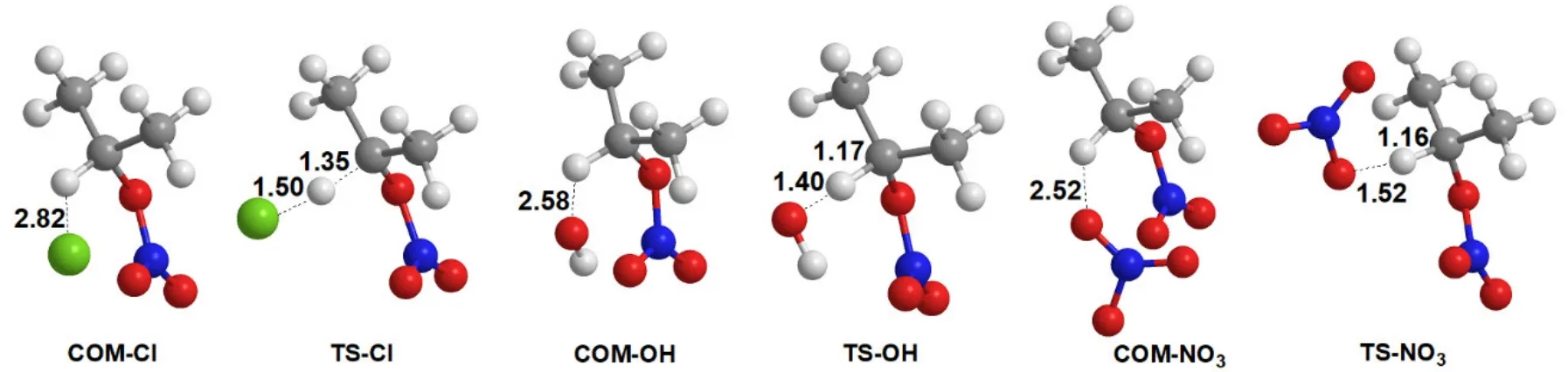
图1 硝酸异丙酯与Cl原子、OH和NO3自由基反应过程中复合物、过渡态的优化构型(键长：Å)

进一步采用CCSD(T)/6-311++G(d,p)方法计算各驻点的单点能。Gaussian程序计算得到的“电子能量”(εele)包括四项：电子的动能、电子与电子间的库仑互斥能、核与核之间的库仑互斥能、电子与核之间的库仑吸引能，即算电子能量的时候是完全忽略核的运动的。但事实上，分子在0 K时仍在平衡位置振动，因此考虑零点能校正(zero-point energy，简称ZPE)。

式中，h为普朗克常数，vi为分子的振动频率，对于线性分子，i等于3N− 5，对于非线性分子，i等于3N− 6，N为分子中的原子个数。

表1所示为IPN + Cl、IPN + OH、IPN + NO3三个反应体系中反应物、过渡态的电子能量εele、零点能ZPE、电子能量和零点能之和，以及过渡态相对于反应物的相对能量(取反应物能量之和为零点，过渡态的相对能量即为反应能垒)。图2(a)为不含零点能校正的势能剖面图，图2(b)为考虑零点能校正后的势能剖面图[5]。从表1及图2可以看出，不含零点能时，IPN + Cl、IPN + OH、IPN + NO3三个反应的能垒分别为15.77、7.98和25.88 kJ·mol−1，加上零点能以后，其能垒分别变为−5.03、2.27和20.10 kJ·mol−1。可见，零点能校正对于得到准确的势能面以及可靠的动力学数据是十分必要的，当然，势能面的准确性与所选用的计算方法也有很大关系。

表1 IPN + Cl、IPN + OH、IPN + NO3三个反应体系中反应物、过渡态的电子能、零点能及相对能量

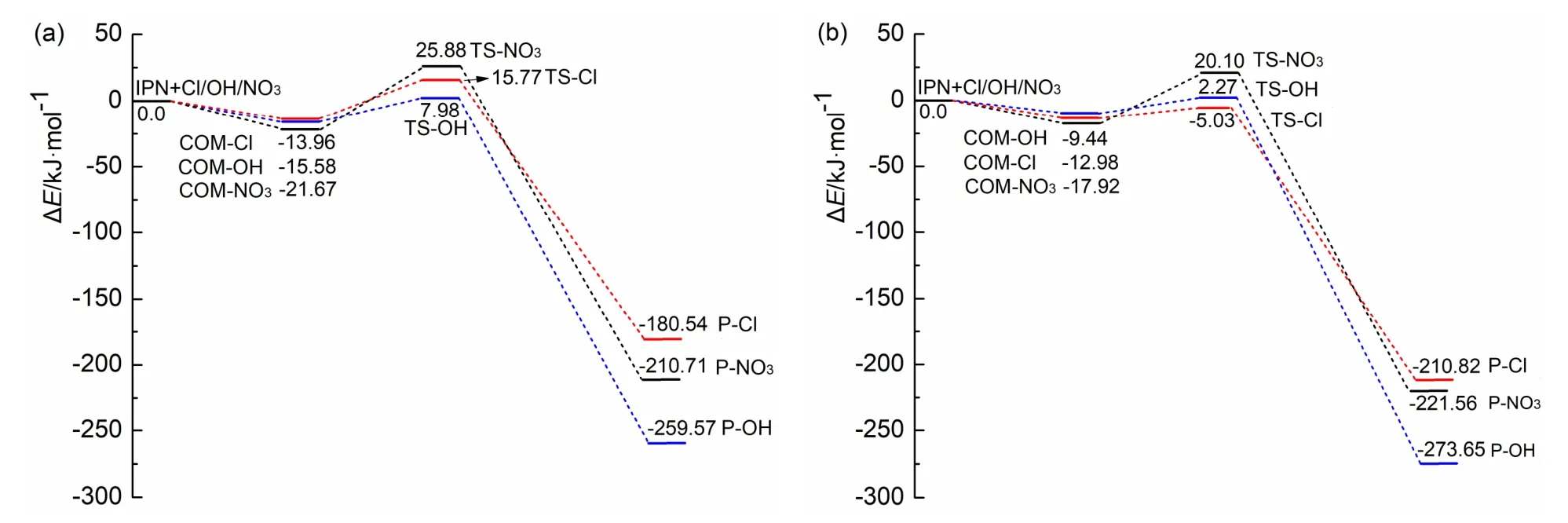
图2 硝酸异丙酯与Cl原子、OH和NO3自由基反应的势能剖面图

3.2 硝酸异丙酯与Cl原子、OH和NO3自由基反应的动力学特征

采用传统过渡态理论，结合Eckart隧道效应，计算了200–500 K温度范围内Cl原子、OH和NO3自由基分别提取硝酸异丙酯IPN的α-H原子的速率常数k，k随温度变化曲线如图3所示[5]。图3(a)将三个反应的速率常数曲线放在一起进行对比；为了更清楚地描述三个反应的速率常数随温度变化趋势，分别将k随温度变化曲线绘制于图3(b)、3(c)和3(d)。

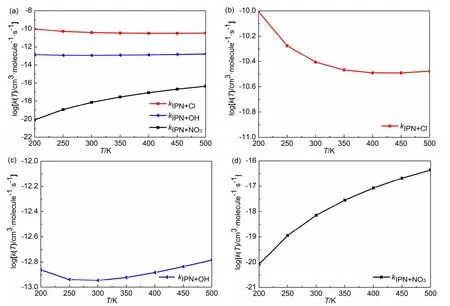
图3 硝酸异丙酯与Cl原子、OH和NO3自由基反应的速率常数与温度的关系

由图3可以看出以下变化趋势：

(1) 图3(a)中，在200–500 K温度范围内，IPN + Cl、IPN + OH和IPN + NO3三个反应的速率常数依次减小，显然，这是由于三个反应的能垒(−5.03 ＜ 2.27 ＜ 20.10 kJ·mol−1)依次升高导致的；

(2) 结合图3(b)、(c)、(d)分析发现，IPN + NO3、IPN + Cl、IPN + OH三个反应的速率常数在200–500 K温度区间内的变化范围分别为：8.29 × 10−21–4.37 × 10−17、9.86 × 10−11–3.34 × 10−11、1.38 × 10−13–1.64 × 10−13cm3·molecule−1·s−1，即速率常数随温度变化的幅度(斜率)依次为：IPN + NO3＞ IPN + Cl ＞ IPN + OH。这是由于IPN + NO3反应能垒的绝对值最大，而IPN + OH能垒的绝对值最小。显然，这些结论与Arrhenius公式结论是一致的。

(3) 另外，由图3(b)、(c)和(d)可以看出对于IPN + OH和IPN + NO3反应，速率常数随温度升高而增大(200 K时，IPN + OH反应具有较高的速率常数是由于低温下隧道效应显著造成的)，而对于IPN + Cl反应，速率常数随温度升高而减小，这是由于IPN + OH和IPN + NO3反应能垒为正值、而IPN + Cl反应能垒为负值。IPN + Cl反应的速率常数呈现负的温度效应，很多包含自由基的基元反应具有这种现象，如克里奇中间体CH2OO与HCHO、H2S的反应[8]，异丁烯醛与OH[9]、Cl原子[10]的反应等，其过渡态的能量低于反应物能量，反应速率常数均随温度的升高而降低。