基于双向流固耦合的无拉索天线桅杆风致振动特性研究
2024-03-04杨雨春王杰胡凯
杨雨春,王杰,胡凯
(四川大学机械工程学院,四川 成都 610065)
天线桅杆一直被用作无线电、电视和其他通信天线的支撑结构[1]。带拉索天线桅杆是常用的天线桅杆结构,de Olieira 等[2]采用有限元法求解了带拉索桅杆的动力学问题。但带拉索的天线桅杆因对安装场景有一定的要求,无法适用于场地较小的工况。无拉索天线桅杆的需求被突显出来。天线桅杆的外形多为钝体,且无拉索天线桅杆顶部由于失去了拉索的固定,桅杆结构在风载荷作用下与风场发生相互作用,会产生更加复杂的动态响应。Williamson[3]对弹性支撑的刚体圆柱在流场中的涡激振动问题上进行了充分的研究。ZHAO 等[4]研究了不同迎流攻角下弹性支撑的刚体圆柱的流致振动问题。Parkinson 和Smith[5]对方柱在流场中响应进行了研究,发现引起驰振的原因为方形截面瞬时来流的不对称性。卫昱含等[6]对不同迎流攻角下正三角柱的流致振动进行二维数值模拟研究,分析了正三角柱的横向振幅、振动频率等特性。端玉木等[7]通过在水槽中不同折合流的实验比较了不同截形状钝体的流致振动特性。李岳霖等[8]考虑了双向流固耦合情况下圆形换热管束的流致振动三维数值模拟研究。现有研究大多集中于拉索的天线桅杆,而对钝体在流场中的动力学响应研究中,也大部分集中于弹性支撑的刚性柱体,柱体截面也多集中于圆形、方形和梯形等。
本文基于双向流固耦合对正六边形的无拉索桅杆在不同风速下的风致振动动力学响应进行分析,得到桅杆在不同风速下的振动位移特性、升力阻力特性以及外围流场特性。
1 无拉索天线桅杆计算模型及固有频率
带拉索天线桅杆模型为一端固支、一端铰支的简支梁,其最大挠度发生在桅杆中部,顶端挠度较小。天线桅杆取消顶端拉索后,边界条件变为固定支撑的悬臂梁,最大挠度容易发生在桅杆顶部。
本文中计算模型的结构和主要尺寸如图1、表1 所示,桅杆共七节,总长L=16375 mm,桅杆截面为空心正六边形,最大截面六方内接圆直径Dmax,最小截面六方内接圆直径Dmin,平均取整截面六方内接圆直径为:

图1 桅杆计算模型示意图

表1 桅杆主要尺寸
表2 和图2 为无拉索天线桅杆前六阶固有频率及对应的振型,前两阶的振型中,桅杆各节同向位移,容易产生较大的桅杆顶部挠度。

表2 桅杆前六阶固有频率
2 无拉索天线桅杆的风致振动
在本文工况下,桅杆受风载变形位移较大,考虑到流场与固体场计算结果会互相影响[9],所以本文基于Fluent、Transient Structural 以及System Coupling 的双向流固耦合方式对桅杆的风致振动特性进行分析。双向流固耦合分析流程如图3 所示,Fluent 在流体域网格上迭代计算流体工况,并将耦合面的上的压力数据通过System Coupling 模块传入Transient Structural模块中,继而在固体域迭代计算桅杆结构的应力、位移等数据。之后Transient Structural 计算得到的桅杆耦合面变形位移结果,再次通过System Coupling 模块传回Fluent 模块。Fluent根据传回的变形位移结果,更新流体计算域网格,并在更新后的网格上重新迭代计算流体工况,再次获得流场变化后的耦合面数据,并将其通过System Coupling 模块传递给Transient Structural 模块计算相应的仿真物理量,重复上述过程直至计算结束。

图3 双向流固耦合求解流程示意图
2.1 计算域、边界条件与重叠网格
双向流固耦合分析过程中,Fluent 需要根据Transient Structural 模块传回的变形位移数据来更新流体域网格,这需要特殊的网格更新技术来实现。常用的网格更新技术为动网格和重叠网格。动网格更新模型有弹簧近似光滑模型(smoothing)、动态分层模型(layering)及局部重画模型(remeshing)[10]。弹簧近似光滑模型中,网格的边被视为截面间相互连接的弹簧,适合于所有类型的网格。动态分层模型根据紧邻运动边界网格层高度的变化,添加或减少动态层来实现动网格,所以只适用于结构化网格。局部重画模型为解决大变形位移,将畸变率过大、尺寸变化剧烈的网格集进行重新划分,适用于四面体网格和三角形网格。重叠网格由背景网格和前景网格相互重叠合并而成,各网格区域相互独立存在[11]。前处理软件将重叠网格处理成洞单元、离散单元及插值单元,流体控制方程各自在背景网格和前景网格上进行求解,插值单元构成内部边界条件,用来传递数据,最终得到整个计算域内的流场信息[12],所以重叠网格对复杂外形部件网格和大位移运动网格生成上有较大优势。
桅杆在较高风速条件下,变形位移较大,变形速率过快,即便采用适用于大变形的局部重画模型也容易产生动网格负体积问题。如果采用较小的时间步长来规避动网格负体积,则会造成计算负担过大,所以本文采用重叠网格技术。图4(a)和图4(b)分别为背景网格部分的X-Y投影面和X-Z投影面,其计算域大小为25D*×16D*×1.1L,局部加密区域尺寸为8D*×8D*×1.1L。为保证尾流的充分发展,桅杆中心距离入口边界5D*,距离出口边界20D*。边界条件设置为:入口为均匀来流速度入口,风速范围为3.5~17.5 m/s;出口为压力出口,出口压力为101325 Pa;远场以及地面均采用对称边界;桅杆耦合面采用无滑移边界条件;湍流模型选择Realizable k-epsilon 模型;壁面函数为可扩展壁面函数。图4(c)和图4(d)为前景网格部分的X-Y投影面和X-Z投影面,其计算域大小为5D*×5D*×(L+3D*),桅杆位于计算域的中心位置。背景网格与前景网格均使用ICEM 划分六面体结构网格。

图4 重叠网格计算域与边界条件
3 结果与讨论
流场初始化采用进口速度标准初始化,所以在流场介质接触固体桅杆时,会产生瞬时载荷加载的瞬态响应,故舍弃桅杆前1 s 响应结果,再对桅杆响应的振幅和受力数据进行分析。
图5(a)为无拉索天线桅杆的横向无量纲振幅X/D*随风速U的变化情况。桅杆的横向无量纲振幅最大值Xmax/D*和均方根Xrms/D*变化趋势一致,均整体随风速的增大而增大。但当U=11.5 m/s 时,横向无量纲振幅出现局部极大值;当U=13.5 m/s 时,横向无量纲振幅出现局部极小值,与整体变化趋势相反,这与桅杆振动模态的转换有关,可以很明显地在桅杆的横向振动位移的频谱图中观察到。在较小风速段(3.4 m/s≤U≤11.5 m/s)时,桅杆振动形式为第一阶模态,桅杆各节同向运动,横向无量纲振幅随风速的增加速度较小;在大风速段(13.5 m/s≤U≤17.5 m/s)时,桅杆的振动形式为第一阶模态和第二阶模态的叠加形式,且第一阶模态占主要形式,横向无量纲振幅随风速的增加速度较大。
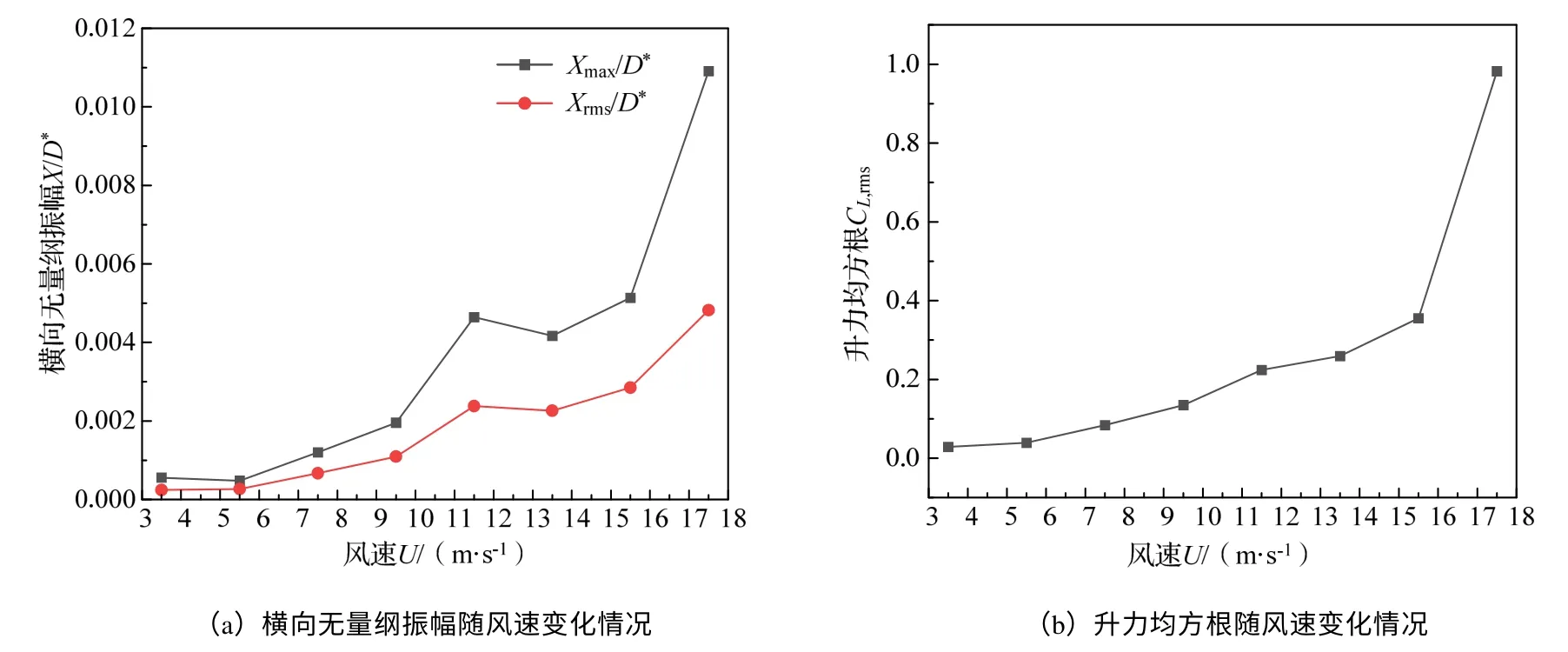
图5 横向无量纲振幅及升力均方根随风速变化情况
图5(b)为无拉索天线桅杆所受升力均方根CL,rms随风速的变化情况。其变化趋势为随风速增大而增大,且在风速U=13.5 m/s 时,图像出现拐点,升力增加速度较之低风速区间减缓,并在高风速段(13.5 m/s≤U≤17.5 m/s)以更大增速增加。桅杆所受升力的变化情况与其横向无量纲振幅相符,在一定程度上可解释横向无量纲振幅中出现极值点的情况。
图6(a)为无拉索天线桅杆的顺风向无量纲振幅Y/D*随风速U的变化情况。其最大值Ymax/D*和均方根Yrms/D*变化趋势依旧一致,随风速的增加单调递增,且并未出现局部极值。在均匀风场中,桅杆变形位移方向与风速方向一致,振动形式为第一阶模态,振幅随风速增加的速度较大。
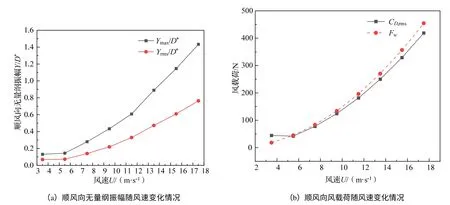
图6 顺风向无量纲振幅及风载荷随风速变化情况
对于露天设备机架所受风载荷有经验计算公式[13]为:
式中:Fw为露天设备机架所受风载荷;C为风力系数,与机架截面形状和细长比有关;Kh为考虑风压高度变化的系数,与地区、地貌有关;A为垂直与风向的迎风面积;q为计算风压,计算公式为:
式中:ρ为空气密度;vs为计算风速。
图6(b)为天线桅杆风载阻力均方根CD,rms及经验风载荷Fw随风速变化情况。数值模拟结果与经验公式基本吻合,最大误差8.5%,造成误差的主要原因是经验公式的迎风面积取值为变形前、而桅杆变形后迎风面积有所减小。桅杆所受风载阻力均方值趋势与顺风向无量纲振幅相符,随着风速增加而单调递增。阻力均方根在风速3.5~17.5 m/s 中,最小值为42.11 N、最大值为481 N。
图7 为无拉索天线桅杆在不同风速下的横向振动位移频谱图。在较小风速段(3.5 m/s≤U≤11.5 m/s)桅杆横向振动完全锁定在第一阶固有频率,桅杆以第一阶模态形式振动;当风速U=13.5 m/s 时,振动位移频谱图中除第一阶主振频率之外,出现了第二副频率f=4Hz,与桅杆第二阶固有频率相等;之后的较大风速段(13.5 m/s≤U≤17.5 m/s)皆为桅杆第一阶固有频率为主频并伴随第二阶固有频率为副频率的多模态振动,桅杆振动形式为第一阶模态与第二阶模态的叠加形式。因为在风速U=13.5 m/s时桅杆发生了振动形式的转换,所以桅杆横向无量纲振幅在此风速下出现了极小值,之后在转换后的振动形式下随风速的增加而增加。桅杆横向振动位移的频谱图可以很好地解释其横向振幅随风速变化的现象。

图7 不同风速下桅杆横向振动位移频谱图
图8为风速U=17.5 m/s下桅杆各高度截面速度云图及流线图。空气流接触桅杆外表面后受正六边桅杆阻挡沿着±30°夹角壁面流动,直到六边形桅杆壁面转角处,桅杆外表面形状发生骤变,对流体的阻挡挤压作用突然消失,在此转角处出现较大的逆压力梯度,然后在桅杆上下两个转角处形成对称的两个高速壁角涡。后续近壁面层流体绕过上次两个高速壁角涡向后流动,在桅杆后体形成低流速区域引发回流,进而发展出两个旋向相反的低速尾流主涡。与圆柱扰流不同,在桅杆尾流部分并未出现交替脱落的漩涡涡街。而是在扰动下两个后体主涡大小交替变化,尾迹不断摆动,进而形成脉动横向力。
4 结论
本文以无拉索天线桅杆为研究对象,进行固有频率分析和基于双向流固耦合的风致振动分析。天线桅杆在较低风速下(3.5 m/s≤U≤11.5 m/s)以第一模态形式振动,且横向和顺风向的振幅均随风速的增大而增大;在风速U=13.5 m/s,桅杆振动形式发生改变,由第一阶模态振动形式转变为第一阶模态和第二阶模态的叠加形式;桅杆横向振幅在振动形式改变时出现下降趋势;在高风速(13.5 m/s≤U≤17.5 m/s)继续随风速增加而增加。而桅杆顺风向振幅在振动形式改变时只出现了增长速度变慢,整个实验风速段均随风速的增加而增加。
基于双向流固耦合得到的桅杆所受风载阻力与机械设计手册中的经验公式基本吻合,最大误差为8.5%,这是因为经验公式带入计算的迎风面积为变形前,所以仿真结果小于经验公式计算值。
在对桅杆的外围流场分析中可知,桅杆上下壁面突变处形成了两个高速壁角涡,在后体尾流部分形成了一对尺寸交替变化的低速尾流涡。因此尾流的交替摆动是造成脉动横向力的主要原因。
