非财务信息在上市公司比较法中应用的难点与解决方案
2024-03-04田文韬
田文韬
(大连财经学院会计学院,辽宁大连 116622)
一、引言
20 世纪80 年代初,美国金融市场掀起了新一轮的并购和重组活动。为了支持这些交易,投资银行和咨询公司开始寻找更快速便捷的方法评估企业价值,相对估值法因而得到了广泛应用。时至今日,相对估值法仍然是当代金融领域内重要的估值方法。然而40 余年来,实务中在使用相对估值法评估企业价值时所采用的价值比率基本全部为财务价值比率,例如市盈率(P/E)、市销率(P/S)、市净率(P/B)等,这实际上是基于企业公开披露的财务信息能够很好地概括企业全貌这一基本假设。诚然,财务信息对企业的确具有一定概括性,主要是因为它综合了企业的各个方面,以简明扼要的方式呈现,并具有相对更直接的可比性以及决策导向。相比之下,纷繁复杂的非财务信息则难以同时具备上述优点,这使得财务价值比率成为评估企业价值和进行决策的重要工具。
随着时间的推移,在财务信息依旧占据重要地位的同时,非财务信息的重要性也在急剧上升。概括来讲,主要是以下三个方面的原因:首先,财务信息只能提供企业财务状况和业绩的一部分,而非财务信息可以提供企业社会责任、环境影响、创新能力、品牌价值等补充信息,能够更好地反映企业的长期价值和可持续发展能力。其次,利益相关方对企业的非财务信息披露提出了更高的期望,企业如果能够积极披露和管理这些信息,将有助于建立良好的企业形象和声誉,从而提高企业估值。最后,自然语言处理与文本挖掘技术的发展逐渐为非财务信息的运用补上了“最后一公里”的短板,主要以文字和图表形式表示的非财务信息可以得到更加高效的挖掘、量化和分析。综上,仍然单纯倚重财务价值比率估算企业价值有失公允,探索如何综合运用财务价值比率与非财务价值比率是未来估值实务的必然趋势。正因如此,立足于强化非财务信息在估值中的作用并增强上市公司比较法的科学性,本文基于上市公司比较法使用程序选取其中三个涉及运用非财务信息的代表性环节,借用专门处理“少数据”“贫信息”不确定性问题的灰色数学和模糊数学,探讨非财务信息如何糅入上市公司比较法关键流程之中,以期为该领域研究提供参考。
二、非财务信息在上市公司比较法中应用的难点
根据《资产评估执业准则——企业价值》,上市公司比较法是指获取并分析可比上市公司的经营和财务数据,计算适当的价值比率,在与被评估单位比较分析的基础上,确定评估对象价值的具体方法。其应用程序如下:第一,搜集上市公司信息,选取和确定比较样本公司;第二,分析比较样本公司和待估对象,选取比较指标,确定比较体系;第三,通过每个样本公司的股权市场价值、全投资资本市场价值与每项指标计算各指标对应价值比率;第四,对各样本公司的价值比率进行加权平均,确定标的公司对应的价值比率;第五,对标的公司每个指标参数乘以对应的价值比率,得到评估对象未扣除流动性的估值;第六,考虑流动性折扣和控股权溢价调整后,确定评估对象的评估值。
从上市公司比较法的应用程序看,第一步、第二步和第三步中可能会添加使用非财务信息。
第一步中可比公司的选择实质上是一个有限方案多目标决策过程。首先,企业价值评估是企业整体评估,其特点是将待评估的企业作为一项完整的独立资产,把企业整体获利能力作为特殊商品进行的评估,而决定企业整体获利能力的因素是多方面的,既包括财务维度也包括非财务维度,因此可比公司的选择需要从多角度考察可比性。目前实务中可比公司的选择标准主要来自财务维度,大致包括所属行业、业务结构、经营模式、企业规模、资产配置和使用情况、企业所处经营阶段、成长性、经营风险、财务风险等方面。前文已述,财务信息对企业获利能力的反映程度是有限的,尤其对一些初创企业或新兴行业。例如对于互联网公司,梅特卡夫定律表明网络的价值与联网的用户数的平方成正比(乔海曙,吕慧敏,2014),用户数构成了互联网公司之间可比的重要条件,继而有学者(陈玉罡等,2019)使用月活跃用户数(Monthly Active User,简记为“MAU”)或每用户平均收入(Average Revenue Per User,简记为“ARPU”)构建非财务价值比率评估,诸如京东、拼多多等亏损互联网上市公司。但是,并非所有非财务信息都像MAU 和ARPU 一样天然可以用精确数值表示,很多非财务信息只能明确它的大致取值范围甚至本身只是以定性描述呈现的。
其次,基于排除个别交易偶然性以及成本效益原则的综合考虑,可比公司的选择通常存在一个有限的范围,实务中普遍选取3-4 家公司作为可比公司(刘灿灿,徐明瑜,2020)。选取可比公司本质上是一个分类的过程,被评估公司和可比公司的相似性用一个综合的“距离”来衡量。“距离”越小,相似性越强,则可比性越强,反之亦然。为增强决策的客观性和科学性,学者们陆续将一些数理方法引入“距离”的计算中,例如模糊集合贴近度(张鼎祖,2005)、多元线性回归(王晓婷,毕盛,2018)、灰色关联分析(胡晓明,等,2020)、优劣解距离法(田文韬,2021)、主成分分析(梁美健,郭文,2021)等。然而,这些数学方法赖以分析的指标基本全部为财务指标,缺乏非财务指标的融入,故所选择的可比公司可以说只是在财务表现上接近于被评估公司。此外,需要注意的是,分类后不代表类内各公司没有差距,各可比公司可比性的差距在第四步计算价值比率的加权平均值时将通过权数反映出来①可比公司可比性差异在第一步确定,在第四步计算时直接使用第一步确定的权重,因此第四步不算作运用了非财务信息。。
第二步与第三步是紧密相连的,第二步建立包含非财务信息的比较体系,第三步则在第二步的既定结果上量化各单个价值比率。目前实务中普遍选择1-4 个价值比率(刘灿灿,徐明瑜,2020),若要加入非财务价值比率,则既要考虑如何量化重要的非财务信息,又要考虑各项财务或非财务价值比率在比较体系中的权重,这两方面问题与第一步非常相似,此处不再赘述。
综上所述,上市公司比较法中第一步为可比公司选择相关问题,具体包括如何利用非精准量化的非财务信息选择可比公司和可比性差异如何确定。第二步为价值比率选择相关问题,同时包括由多个价值比率构成的比较体系如何分配权重。第三步为非财务信息的量化问题,即如何将非精准量化的非财务信息精确量化并计算非财务价值比率。
三、区间灰数模糊聚类在步骤一中的应用
非财务信息按其初始形式的不同可分为已精确量化的非财务信息和未精确量化的非财务信息,未精确量化的非财务信息可能表现为区间值或定性描述形式。对于定性描述的非财务信息可以通过诸如专家打分的方法量化为精确值或区间值,而精确值可视为区间值的特殊形式,即区间下限等于区间上限。此时可比公司选择问题即转化为区间灰数聚类问题。
引入区间灰数后,可比公司之间的类别界限更加不分明,这类问题适合进行软分类。模糊数学的产生为软分类提供了数学基础,由此产生了模糊聚类分析(李相镐等,1994)。因此本文推崇采用区间灰数模糊聚类方法解决步骤一中的问题。
(一)相关概念界定
1.区间灰数
灰数是灰色系统理论中的重要概念,用于描述人们对灰色系统认识的不确定性程度。在系统研究过程中,由于人的认知能力有限,对反映系统行为的信息难以完全认知,所以人们只知道系统元素或参数的取值范围,通常把这种在某个区间或某个一般数集内取值的不确定数称为灰数。区间灰数定义如下:
定义1 记a~∈ [aL,aU]={x|aL≤x≤aU,aL,aU∈R},称a~为一个区间灰数,特别地,若aL=aU,则a~退化为一个白数。
2.模糊关系
模糊关系是一种描述事物之间模糊联系的数学工具。在现实世界中,很多事物或概念的属性不是非黑即白的,而是存在一定程度的模糊性。模糊关系的目的就是用数学方法来描述这种模糊性。常见的模糊关系包括模糊等价关系和模糊相似关系等。定义如下:
定义2 设是论域X 上的一个模糊关系,若满足:
则称是X 上的一个模糊等价关系。其中,表示模糊子集的隶属函数。若只满足自反性与对称性,则称是X 上的模糊相似关系。
当X={x1,x2,…,xn}时,模糊相似关系可以用模糊矩阵表示。由自反性与对称性不难知道,N 是主对角线上的元素均为1 的对称模糊矩阵,即nii=1,nij=nji,这样的模糊矩阵称为模糊相似矩阵。
(二)区间灰数模糊聚类在步骤一中的应用程序
第 一,设X={x1,x2,…,xn}为备选公司集,U={u1,u2,…,um}为可比性评价集,对备选公司xi(i=1,2,…,n),按属性uj(j=1,2,…,m)进行测度,确定xi关于uj的属性值,从而得到样本数据矩阵
第二,最常见的属性值包括效益型(越大越好)和成本型(越小越好)两类,为消除量纲并增加可比性,采用如下灰色极差变换方法对进行标准化处理得到规范化矩阵
第三,利用区间灰数最大最小法相似系数(杨俊杰,2009)计算的模糊相似关系矩阵N=(nij)n×m。计算方法如下:
其中,、均为m 维区间灰数向量,易证由式(3)求得的模糊相似关系矩阵满足自反性与对称性,但不满足传递性。
第四,使用模糊传递闭包法,将模糊相似关系矩阵转为模糊等价关系矩阵。因为将模糊相似关系转化为模糊等价关系可以简化问题、提供决策依据,并更好地保留信息。这样可以使问题更易处理,并提供了一定的依据和参考,有助于进行决策和分析。
第五,根据方案优劣排序进行选择和确权。
(三)案例分析
甲公司是中国一家尚未上市的大型造纸企业,为解决甲公司的发展资金需求,甲公司有意引进某投资人,以进一步推动公司业务的发展。该投资人也有意对甲公司进行投资,因此委托国内某评估机构对甲公司的股东全部权益价值进行评估,资产评估的部分摘要如下:
评估目的:为委托人拟实施增资事宜提供评估对象的市场价值参考依据。
评估对象:甲公司的股东全部权益价值。
评估范围:甲公司评估基准日拥有的全部资产及相关负债。
价值类型:市场价值。
评估基准日:2023 年12 月31 日。
评估师从A 股“造纸及纸制品业”上市公司中初步遴选出6 家与甲公司经营范围近似的上市公司,为了进一步增强各方面的可比性,评估师考虑了如下5 个与造纸行业关系密切的非财务指标确定甲公司的可比公司①为演示非财务指标如何量化使用,此处暂不加入财务指标。:供应链稳定性u1(水平),“三废”治理技术u2(水平),政企关系u3(水平),员工患尘肺病概率u4(百分比)和客户投诉率u5(百分比)。其中,u1、u2和u3为效益性指标,u4和u5为成本型指标。
u1、u2和u3天然不是以定量形式表现,可以构造Likert5 级量表由专家进行打分。u4和u5可以首先从各公司披露的社会责任报告、媒体报道、中国造纸学会和中国造纸协会公布的数据,各大公开数据库等搜集数据,对无法收集的,由专家大致估算区间值。最终各公司的指标量化区间值如表1 所示②数据并非真实,可能与行业情况不符,仅用于演示应用过程。。
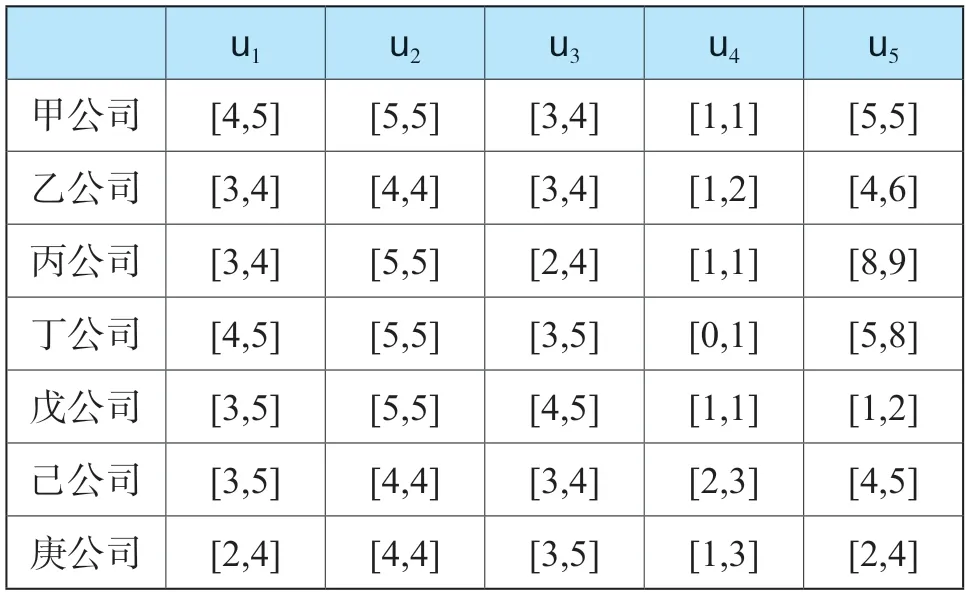
表1 各备选公司指标量化区间值
通过式(1)和式(2)进行灰色极差变换,得各公司的标准化指标区间值如表2 所示。

表2 各备选公司标准化指标区间值
得到规范化矩阵:
通过式(3)计算的模糊相似关系矩阵如下:
此时,从矩阵N 的第一行可以得出这样的结论:备选公司乙、丙、丁、戊、己和庚相对甲公司的贴近度分别为0.54、0.73、0.87、0.78、0.51 和0.43。进一步,利用平方法求N 的最小传递闭包N*如下:
虽然λ 取不同值会得到不同的λ 水平截集和聚类结果,但甲公司的可比公司可比性的顺序是不变的,即:丁公司Φ 戊公司Φ 丙公司Φ 乙/己/庚公司。假设评估师拟选取3 家可比公司,由此可确定可比公司丁、戊和丙的可比性权重:
该权重值将在第四步对各可比公司的价值比率进行加权平均时用到。
四、离散灰数灰靶决策在步骤二中的应用
如果评估师拟选择多个价值比率进行估值(可能既包括财务价值比率也包括非财务价值比率),就需要考虑使用哪些价值比率以及这些价值比率的权重是否相同。某一价值比率对于评估的意义在于它的代表性、相关性和重要性等方面。虽然第二步与第一步面对的问题类似,但需要注意的是,在对可比公司可比性评价时,先前的实务和研究中依靠相关定量财务信息和数学方法尚可得出较为科学客观的结论,而对价值比率代表性、相关性和重要性的评价无任何定量数据可供使用,更像是在一个没有任何量化信息背景下依据经验和直觉的纯定性判断。研究中对于这种无定量信息的决策问题多使用层次分析法,然而层次分析法必须要将所有价值比率两两比较并打出一个精确的比较标度,这为评估工作增添了一定复杂性和操作难度。因此本文推崇采用离散灰数灰靶决策方法解决第二步中的问题。
(一)相关概念界定
1.离散灰数区间评价
在某一区间内取有限个数值的灰数称为离散灰数。
价值比率的权重差异本质上反映了各价值比率对评估对象的代表性、相关性和重要性程度差异。在现实决策中,通常我们无法直接定量地给出比较体系中诸价值比率的权重。对于某一价值比率,我们初步可以得到的是其对于评估对象的直观重要程度,如在对某价值比率的重要性进行评价时,设其对评估对象的重要性程度集合为{非常重要,重要,一般,不重要,非常不重要}。因为不同专家在该价值比率对于比较体系的重要性认识不尽相同,所以分析权重时可以获得的初步信息表现为一离散灰数。
若已知一价值比率的重要性评价维度的评价下限集合为P={一般},评价上限集合为Q={一般,重要},则可记该价值比率重要性维度的离散灰数区间评价为,正式定义如下:
定义3 若某对象的离散灰数下限评价为P,上限评价为Q,则该离散灰数区间评价可以记为(P,Q 为集合,P⊆⊗⊆Q)。
2.灰靶决策
定义4 记方案Ai的效果向量ri与靶心r0的下限距离为:
上限距离为:
则综合靶心距离为:
其中,k 为最高评价等级,pij为方案Ai在评价维度j 的下限集合,lij为方案Ai在评价维度j 的评价上限集合与评价下限集合的数量差值,i=1,2,…,n,j=1,2,…,m。
(二)离散灰数灰靶决策在步骤二中的应用程序
第一,根据被评估公司的个体和行业等特征选取若干财务与非财务价值比率。
第二,对备选价值比率的代表性、相关性和重要性三个维度采用Likert5 级量表进行打分。由于三者皆为效益型目标,因此统一为数值越大则评价越高,例如对价值比率重要性的评价可设为S={5,4,3,2,1}={非常重要,重要,一般,不重要,非常不重要}。由于不同专家对同一价值比率的重要性认知很可能存在差异,因此评价结果表现为离散灰数区间评价j=1,2,…,m),其中Pij和Qij分别表示⊗ij的效果评价值的下限评价和上限评价。
第三,选择β,计算各项价值比率的综合靶心距,依据靶心距对各价值比率进行筛选和确权。
(三)案例分析
接上节案例,评估师经讨论和调查初步列出了6 个可能使用的价值比率,拟在评估时从中选用4 个代表性强、相关性强和重要性强的价值比率。评估师向有关专家发放Likert5 级量表对这6 个价值比率3 个维度进行打分,结果如表3 所示①数据并非真实,可能与行业情况不符,仅用于演示应用过程。:

表3 备选价值比率各属性区间评价
其中,∅为评价缺失时的值,Ω 为全部的评价等级集合,即{5,4,3,2,1}。
理论上,不完备信息系统区间评价可能出现两种极端情况:
其一,各打分专家对某一价值比率的某一属性完全无法判断,即该价值比率的某一评价值信息完全未知,例如⊗11。此时认为该价值比率此属性评价的下限为最低分1 分,上限为Ω,即:
其二,各打分专家对某一价值比率的某一属性判断完全一致,例如⊗41和⊗42,则该价值比率此评价值信息退化为白数,即:
由于我们对评价值的下限和上限没有明显偏好,故β 取0.5。
基于上述数据与分析,利用式(4)、式(5)和式(6)计算各备选价值比率的综合靶心距分别为:“P/E”综合靶心距为4.33,“P/S”综合靶心距为1.80,“P/B”综合靶心距为1.87,“P/纸浆得率”综合靶心距为0.71,“P/社会责任评分”综合靶心距为2.65,“P/顾客满意度”综合靶心距为3.84。依据综合靶心距进行排序,可得:P/纸浆得率ΦP/SΦP/BΦP/社会责任评分ΦP/顾客满意度ΦP/E。
靶心距实际上属于负向指标,为确定权重,对6个价值比率的靶心距正向化处理,方法如下:
使用正向化后的靶心距计算前四位价值比率的权重如下:
该权重值将在第六步对各价值比率进行加权平均以求出最终评估结果时用到。
五、区间灰数白化在步骤三中的应用
引入区间灰数概念后,非财务信息在一定程度上得以量化,而区间灰数的白化为构造非财务价值比率创造了可能。
灰数白化是一种区间灰数处理方法,用于将区间灰数转化为确定性的数值。白化方法可以通过对区间灰数进行适当的处理和转换,得到一个代表不确定性程度的确定性数值。其基本步骤如下:
第一,确定区间灰数的上界和下界,表示不确定性范围。对于分母尚未精准量化的非财务价值比率采用估计或Likert5 级量表专家打分等方式得出分母非财务信息的区间灰数。
第二,根据具体情况选择适当的白化方法,常见的方法包括均值白化(刘思峰等,2017)、面积-坐标转换法(张军,曾波,2012)等。
第三,对区间灰数进行白化处理,得到一个确定性的数值。
第四,根据白化后的数值构建非财务价值比率。
此步骤借鉴区间灰数白化的处理方法后计算较为简单,限于篇幅,不进行举例说明。
六、总结
随着上市公司比较法中单纯运用财务价值比率评估企业价值的弊端日益凸显,非财务价值比率的构建与运用愈加重要。本文在分析上市公司比较法运用程序的基础上,发现在上市公司比较法中可比公司选择及其可比性评价和价值比率比较体系构建及其权重确定,即上市公司比较法的第一步、第二步和第三步中会涉及添加使用非财务信息。基于此,本文借用专门处理“少数据”“贫信息”不确定性问题的灰色数学和模糊数学,提出使用区间灰数模糊聚类处理可比公司选择及其可比性评价问题;使用离散灰数灰靶决策处理价值比率比较体系构建问题;使用区间灰数白化处理非财务价值比率量化问题。在最大限度结合非财务信息特点的同时,也保留了评价过程的客观性,具有一定的现实意义。
值得注意的是,随着非财务信息越来越重要,量化方案越来越多,可比公司和价值比率的选择可能会越来越复杂,这就进一步对评估机构和评估专业人员提出了两点要求:首先,要明确可比公司的选择和价值比率比较体系的构建均既需要克服偶然性同时又需要把握成本效益原则;其次,抓主要矛盾,洞穿影响可比性和价值的决定性因素。
