考虑建成环境的电动自行车事故严重程度致因分析

2024-03-03王菁董春娇李鹏辉姜文龙邵春福

交通运输系统工程与信息 2024年1期

王菁，董春娇*，李鹏辉，姜文龙，邵春福,3

(1.北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.中国人民公安大学，治安与交通管理学院，北京 100038；3.新疆大学，交通运输工程学院，乌鲁木齐 830017)

0 引言

电动自行车具有低价、便捷、灵活、环境友好等优点，已成为居民日常通勤的重要交通方式及低碳交通的重要组成部分。截止2020 年，我国电动自行车保有量已超过3亿辆。然而，随着电动自行车保有量的上升，近年来我国电动自行车交通事故死亡人数占交通事故总死亡人数的比例也不断增长。在此背景下，探究电动自行车事故严重程度的影响因素对降低电动自行车事故严重程度具有重要意义。

国内外学者已针对电动自行车交通事故严重程度影响因素展开了诸多研究。QIAN等[1]采用广义有序Probit模型，从事故画像、自然环境、道路特征、骑行者属性和车辆特征这6个方面分析了电动自行车交通事故严重程度的影响因素。马景峰等[2]加入时间因素的考量，基于偏比例优势模型的结果表明，骑行者性别、骑行者年龄、机动车类别和电动自行车类别是影响电动自行车与机动车碰撞事故严重程度最大的因素。此外，GUO等[3]探究了危险骑行行为和违法骑行行为对电动自行车事故严重程度的影响。然而，上述研究忽略了建成环境的影响。建成环境作为影响城市交通出行需求的重要因素，已被证实可对电动自行车交通事故的分布产生显著影响。例如，PETZOLDT等[4]的研究发现，电动自行车事故起数与道路交叉口密度呈显著正相关关系。何庆等[5]的研究表明，人口密度较高的区域更容易发生电动自行车事故。此外，陈坚等[6]的研究表明，土地利用混合度、道路密度及可达性对城市机动车交通事故严重程度存在非线性影响。潘义勇等[7]发现，在事故发生地300 m 缓冲区内存在购物中心会使男性老年人更容易发生仅财产损失事故。因此，有必要探讨建成环境对电动自行车交通事故严重程度的影响。

在模型选择方面，既有研究多基于离散选择模型建模交通事故严重程度。YUAN等[8]采用二项Logistic模型探究了影响电动自行车与机动车交通事故严重程度的关键因素。CHEN等[9]聚焦行人与机动车碰撞事故，基于多项Logit 模型识别影响其严重程度的主要因素。为克服多项Logit模型的严格IIA(Irrelevant alternative property)假设，温惠英等[10]将巢式Logit模型运用于摩托车单车事故严重程度致因分析中。此外，一些学者构建有序模型以进一步刻画交通事故严重程度的有序特性。WANG等[11]利用中介有序Logit模型研究电动自行车头盔使用及电动自行车碰撞事故的影响因素。RIFAAT等[12]采用广义有序Logit 模型探究影响摩托车碰撞事故严重程度的因素。然而，上述模型假设影响因素对不同的交通事故严重程度的影响相同。在实际中，各影响因素对不同交通事故严重程度的影响存在异质性，忽略这一异质性会导致参数估计结果偏差。为进一步探讨影响因素对事故严重程度的异质性影响，焦朋朋等[13]将随机参数Logit模型运用于老年人交通事故严重程度致因分析中，结果表明，随机参数Logit模型较多项Logit模型有更好的拟合优度。WANG等[14]构建考虑均值异质性的随机参数Logit模型探讨电动自行车交通事故严重程度的影响因素，结果表明，大型货车在重伤事故中具有随机参数特征，当事故同时涉及大型货车及未开起照明灯的机动车时，发生重伤事故的可能性将增加。不同于上述异质性模型，考虑均值异质性及方差异质性的随机参数Logit模型可以同时捕捉随机参数的均值异质性及方差异质性，更全面地解释引起随机参数变化的原因。WASEEM等[15]基于该模型探究了摩托车交通事故严重程度的影响因素，结果表明，摩托车排量的参数在摩托车死亡事故中为随机参数，且具有显著的均值异质性及方差异质性。然而，在中国，摩托车车速远高于电动自行车，且摩托车类属机动车，电动自行车类属非机动车，故两者事故严重程度影响因素存在差异[1]。

综上所述，本文将建成环境纳入电动自行车交通事故严重程度建模中，基于北京市的电动自行车交通事故数据，从事故属性、骑行者属性、对象车辆及驾驶员属性、道路属性及建成环境属性这5个方面，构建考虑均值异质性及方差异质性的随机参数Logit模型探讨电动自行车交通事故严重程度影响因素。研究结果可以为电动自行车交通事故预防提供理论支撑。

1 电动自行车交通事故严重程度时空分布特征

本文基于北京市近5 年抽样得到的5000 起电动自行车交通事故数据展开研究。数据记录了事故的发生时间、发生地点、骑行者信息和对象车辆信息等详细数据。本文仅考虑工作日发生的交通事故，在剔除周末事故、信息缺失事故和明显记录有误的事故后，共得到3218 起电动自行车事故数据用于研究。其中，包含死亡事故386 起，占比11.96%；受伤事故624起，占比19.39%；仅财产损失事故2208 起，占比68.61%。图1 描述了电动自行车交通事故的时空分布情况。如图1(a)所示，电动自行车交通事故主要发生在6:00-24:00，0:00-6:00较少发生事故；此外，3类事故数量均在早晚高峰和午高峰出现峰值，这一结果与已有研究相对应，即电动自行车已成为居民日常通勤的重要交通方式[1]。如图1(b)所示，从空间分布看，仅财产损失事故和受伤事故较死亡事故更集中分布于城中心区域，而死亡事故的分布则相对分散。

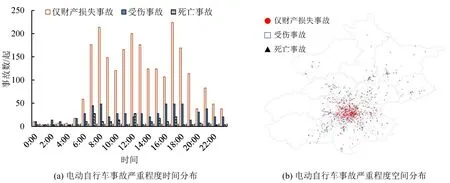
图1 电动自行车交通事故严重程度时空分布Fig.1 Spatiotemporal distribution of e-bike traffic accidents injury severities

基于已有研究，从事故属性(碰撞类型、事故时段)、骑行者属性(性别、年龄)、对象车辆及驾驶员属性(驾驶员性别、年龄以及车辆类型)、道路属性(道路类别、路口/路段及天气状况)和建成环境属性(居住密度、土地利用混合度、路网密度、交叉口密度、公交站密度、地铁可达性、到最近医院的距离及到市中心的距离)这5个方面共选取18个因素探讨电动车交通事故严重程度的影响因素。其中，建成环境变量基于建成环境的5D 要素，即密度(Density)、多样性(Diversity)、设计(Design)、目的地可达性(Destination Accessibility)和公交临近度(Distance to Transit)选取，基于事故发生地500 m 缓冲区计算[6-7,16]。所有变量均由事故数据和兴趣点数据(Point of Interests,POIs)计算得到，变量的描述统计如表1所示。

表1 变量说明Table 1 Description of variables

2 考虑均值异质性及方差异质性的随机参数Logit模型

传统随机参数Logit模型要求影响因素对事故严重程度的影响在不同事故中恒定不变。然而，在实际情况中，由于事故数据中存在未观测到的关键变量(如头盔佩戴情况、事故发生时的交通拥堵状况及驾驶行为等)可能会导致建成环境对电动自行车事故严重程度的影响产生异质性，从而使得参数估计结果产生偏差[15]。与普通的随机参数Logit模型不同，考虑均值及方差异质性的随机参数Logit模型允许随机参数的均值和方差在不同交通事故之间变化，因此，能够更好地捕捉解释变量对电动自行车交通事故严重程度的影响。对于交通事故n，定义其事故严重程度的函数为

式中：Bin为电动自行车交通事故n严重程度为i时的函数，基于已有研究[1,14]，本文将事故严重程度定义为3 个等级，即仅财产损失事故、受伤事故和死亡事故；Xin为在电动自行车交通事故n中影响事故严重程度i的解释变量向量(表1)；βi为解释变量的待估参数；εin为随机误差项。若εin服从广义极值分布，则得到多项式Logit 模型的概率分布形式[13]为

式中：Pin为电动自行车事故n严重程度为i的概率；I为本文考虑的3 种电动自行车事故严重程度的集合。为解释可能的均值异质性及方差异质性，考虑均值及方差异质性的随机参数Logit模型定义βi为随电动自行车事故n变化的随机参数向量，即

式中：β为所有电动自行车事故的参数估计均值；σin为βi的标准差；Zin和Win分别为解释变量在事故n中的均值异质性和方差异质性的向量，分别影响βi的均值异质性及方差异质性；Θin和ωin分别为Zin和Win对应的参数估计向量；vin为干扰项。

目前，国外果蔬运输所用的运输工具主要是冷藏汽车和普通卡车，国际间运输主要用冷藏集装箱。我国短途公路运输所用的运输工具包括汽车、拖拉机、畜力车和人力拉车等。汽车主要有普通运货卡车、冷藏汽车和冷藏集装箱。水路运输工具用于短途运输的一般为小船、拖船，远途运销的主要是远洋货轮。铁路运输越来越少。

最后，得到考虑均值及方差异质性的随机参数Logit模型的概率密度函数为

式中：f(βiφi)为βi的概率密度函数；φi为均值异质性及方差异质性的参数向量。在以往的研究中，f(βiφi)常见的分布形式为正态分布、均匀分布、三角分布和单侧三角分布，其中，正态分布是事故严重程度分析中最常用的分布形式[13]。

采用最大似然估计法对考虑均值及方差异质性的随机参数Logit模型进行参数估计(式(4))。由于Halton抽样法较随机抽样更有效，故选取Halton抽样法，抽样次数设置为200[15]。与以往研究一致，设置f(βiφi)为正态分布。

上述得出的回归参数只能定性反映解释变量对电动自行车事故严重程度影响趋势，无法定量描述解释变量对电动自行车事故严重程度发生概率的影响。因此，引入平均边际效应系数以定量描述解释变量的影响，针对连续变量为

当xin为0-1变量时，由于xin不可微，式(5)不可用。对于0-1变量xin，其平均边际效应表示为当xin由0 变化到1 时对事故严重程度i发生概率的影响，即

3 结果与讨论

为防止变量间存在多重共线性导致结果失真，首先利用方差膨胀系数法(Variance Inflation Factor,VIF)进行多重共线性检验。多重共线性检验结果表明，所有变量的VIF值均小于10，因此，可忽略变量间的共线性问题[7]，将所有变量均纳入模型。

为验证模型的有效性，采用Nlogit软件分别构建随机参数Logit 模型、考虑均值异质性的随机参数Logit模型和考虑均值及方差异质性的随机参数Logit 模型进行模型比较。基于赤池信息量准则(Akaike Information Criterion,AIC,越小越优)和收敛的对数似然值(越大越优)评估模型拟合优度。如表2所示，3种模型中，考虑均值异质性的随机参数Logit 模型较随机参数Logit 模型有更小的AIC 值和更大的收敛的对数似然值，考虑均值及方差异质性的随机参数Logit模型的AIC值(818.08)最小，收敛的对数似然值(-375.04)最大。即考虑均值及方差异质性的随机参数Logit模型拟合效果最好。

表2 参数估计结果Table 2 Parameter estimation results

3.1 随机参数

3.2 均值异质性及方差异质性

相较传统的随机参数Logit 模型，考虑均值异质性及方差异质性的随机参数Logit模型能够进一步探究随机参数均值及方差的个体异质性，解释造成随机参数的可能原因。

如表2所示，一般城市道路对于受伤事故的随机参数在路段中存在均值异质性，系数为0.98，即路段将导致一般城市道路的参数均值增加。如图2(a)所示，在一般城市道路的电动自行车交通事故中，当事故发生在交叉口和其他区域时，一般城市道路对受伤事故的参数均值为-1.04，当事故发生在路段时，参数均值为-0.06，即-1.04+0.98=-0.06。因此，发生在一般城市道路的事故将降低受伤事故的发生概率，而事故发生在路段将使这一降低幅度减小。到最近医院距离对于死亡事故的随机参数在路段和恶劣天气中存在均值异质性，系数分别为-0.32和1.51，即路段将导致到最近医院距离的参数均值减小，而恶劣天气将导致到最近医院距离的参数均值增加。如图2(b)和图2(c)所示，到最近医院距离增加将增加死亡事故发生的概率，事故发生在路段将降低这一概率增加的幅度，而事故发生在恶劣天气将进一步增大死亡事故发生的概率。

图2 随机参数均值异质性分布Fig.2 Distribution of random parameters with heterogeneity in means

到最近医院距离的参数在骑行者年龄为(40,60]岁中存在方差异质性，系数为2.25。表明涉及到骑行者年龄为(40,60]岁的交通事故中，到医院距离的随机参数较涉及到其他年龄段骑行者的事故分布更宽，离散程度更大。

3.3 影响因素分析

为进一步量化影响因素对电动自行车事故严重程度的影响，计算各变量的平均边际效应系数，结果如表3所示。

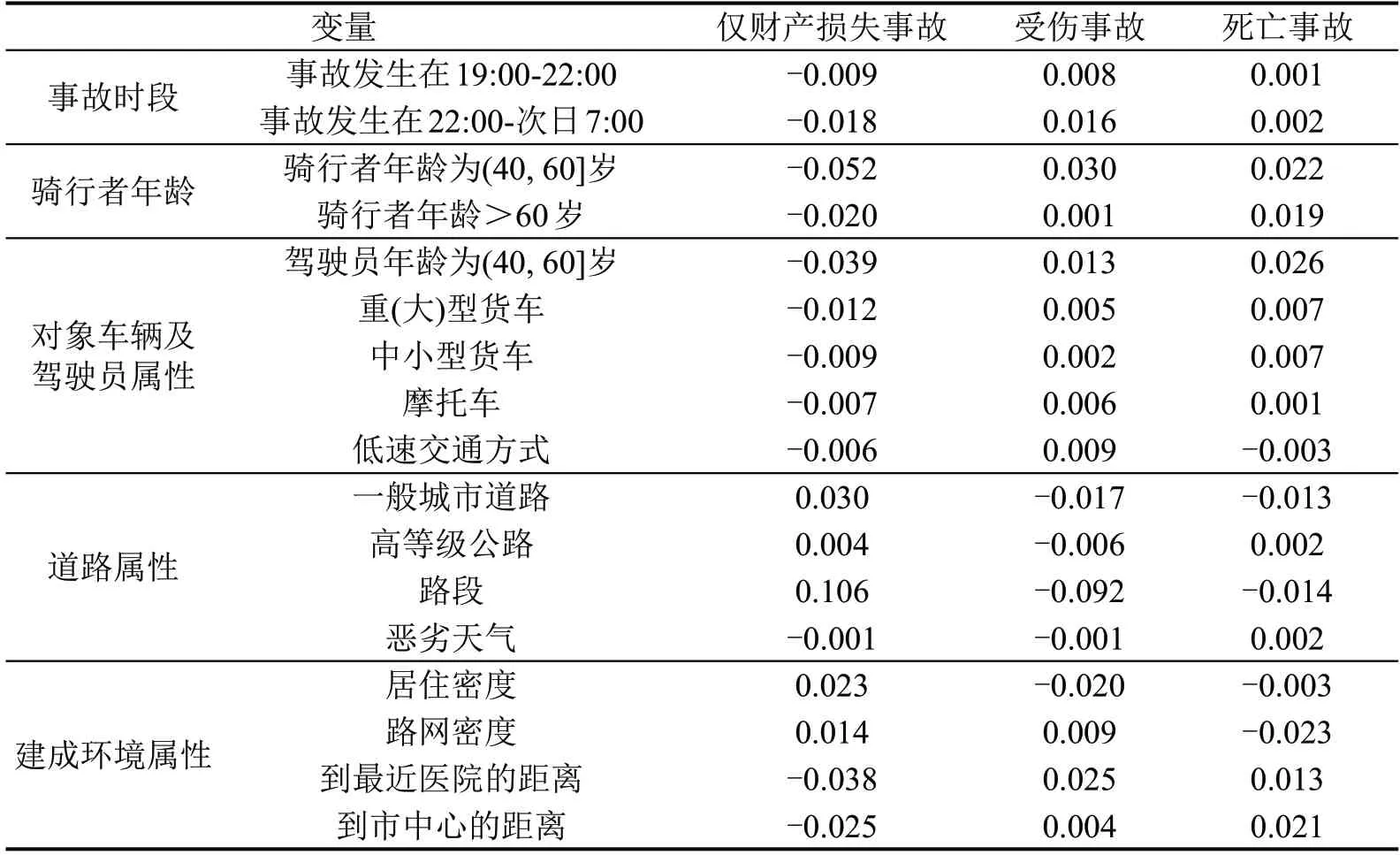
表3 边际效应分析结果Table 3 Results of marginal effects

对于事故属性，相较于其他时段，事故发生在19:00-次日7:00，将降低仅财产损失事故发生的概率。当事故发生在19:00-22:00时，仅财产损失事故发生的概率将降低0.9%，而受伤事故和死亡事故发生的概率将分别增加0.8%和0.1%；当事故发生在22:00-次日7:00时，仅财产损失事故发生的概率降低1.8%，而受伤事故和死亡事故的发生概率将分别增加1.6%和0.2%。可能的原因是夜间道路能见度降低，同时车辆较少，骑行者骑行速度较快，故更容易发生受伤和死亡事故。

对于骑行者属性，与年轻的骑行者相比，骑行者年龄超过40岁将降低仅发生财产损失事故的概率。骑行者年龄为(40,60]岁时，仅财产损失事故的发生概率将降低5.2%，而受伤事故和死亡事故的发生概率将分别增加3.0%和2.2%。骑行者年龄超过60 岁时，发生仅财产损失事故的概率将降低2%，而发生受伤事故和死亡事故的概率将分别增加0.1%和1.9%。这一结论是合理的，随着骑行者年龄的增加，身体健康状况变差，因此将增加事故的严重程度。

对象车辆及驾驶员属性中，相比于其他年龄段，当驾驶员年龄为(40,60]岁之间时，更容易发生受伤事故及死亡事故，其概率分别增加1.3%和2.6%。可能的解释是，随着驾驶员年龄的增大，反应速度下降，因此更容易造成严重的事故后果。当对象驾驶车辆为重(大)型货车、中小型货车和摩托车时，受伤事故及死亡事故发生的概率分别增加0.5%和0.7%，0.2%和0.7%以及0.6%和0.1%，这一结果符合常理，且与之前的研究结论一致[1]。当对象车辆为低速交通方式时，受伤事故的概率将增加0.9%，而仅财产损失事故和死亡事故发生的概率将分别下降0.6%和0.3%。

道路属性中，相比于其他道路类型，事故发生在一般城市道路时，发生仅财产损失事故的概率上升3.0%，而受伤事故和死亡事故的发生概率分别下降1.7%和1.3%。这可能是由于北京一般城市道路限速较高等级道路更低，且较为拥堵，因此，车辆行驶速度更慢，更不容易发生严重的交通事故。当事故发生在高等级公路时，发生受伤事故的概率下降0.6%，发生仅财产损失事故和死亡事故的概率分别上升0.4%和0.2%。这可能是由于本文中发生在高等级公路上的事故主要发生在辅路上，因此与一般城市道路相似，车速较低，进而发生财产损失事故的概率上升，而其余发生在高等级公路上的事故，车速快，因此发生死亡事故的概率上升[2]。此外，发生在路段的事故更容易为仅财产损失事故，而恶劣天气更容易发生死亡事故。

建成环境属性中，居住密度每增加一个单位，发生仅财产损失事故的概率将增加2.3%，而发生受伤事故和死亡事故的概率将分别下降2.0%和0.3%。这是由于发生在高居住密度区域的交通事故，道路限速往往更低(居住区周边道路)，因此发生严重事故的概率降低。路网密度每增加一个单位，死亡事故发生的概率将下降2.3%，仅财产事故和受伤事故发生的概率将分别增加1.4%和0.9%，这与戢晓峰等[16]关于“路网密度更低的区域更容易发生致命事故”的结论一致。到最近医院距离和到市中心距离的增加均会降低仅财产损失事故的概率，增加受伤事故及死亡事故的概率。前者的结论符合认知。后者可能的解释是，城中心的道路基建设施更好，路网密度更高，同时城郊区交通有更多大重型车辆出没，因此距离市中心距离更远更容易发生严重的交通事故。