基于生成对抗网络的追尾事故数据填补方法研究

周备，张莹，张生瑞，周千喜，汪琴

(1.长安大学，运输工程学院，西安 710064；2.北京清华同衡规划设计研究院有限公司，北京 100085)

0 引言

交通事故的频繁发生严重威胁着人们的生命财产安全，制约着经济社会的健康发展，追尾事故作为交通事故中最常见的类型之一[1]，吸引了众多研究者的关注。研究者们旨在通过分析事故历史数据，揭示不同严重程度事故的致因机理，并提出降低事故严重程度的工程或管理措施。但在数据采集、运输、存储过程中往往会因为技术或管理问题造成数据丢失，继而影响后续的建模分析。针对这一问题，众多学者展开了研究，通过填补手段对事故数据缺失值进行处理，以改善数据质量，提高模型预测精度。DEB等[2]提出一种利用事故数据间的相关性来插补数值或分类值的方法，该方法根据数据亲和度对潜在估算值进行采样，能够解释交通事故数据的不确定性。LI等[3]提出一种改进的贝叶斯向量自回归方法对碰撞事故数据缺失值进行填补，该方法能够较好捕获数据集中未观察到的异质性。LUKUSA等[4]提出一种通过参数或非参数获得权重，并基于权重对观测数据进行反向加权，最终实现事故数据缺失值填补的方法。柏伟[5]提出一种改进Apriori 关联规则算法来探究逃逸事故数据的缺失规律，并在此基础上进行数据缺失值的填补。尽管已有数据填补方法在一定程度上改善了数据质量，但仍存在一些局限性。例如，现有方法通常在应对低维度和少量数据时效果较好，但随着事故数据维度和事故数据量的扩充，其填补精度往往会下降，难以满足后续事故数据建模的需求。此外，现有方法通常只适用于特定的数据缺失类型，导致其对某些数据缺失类型不够敏感，适应性较差，填补效果不佳。

2014 年生成对抗网络(Generative Adversarial Network,GAN)的提出，为处理复杂场景下的数据缺失问题提供了可能[6]。经过近几年的发展，生成对抗网络已经迭代出众多衍生模型，并且已有学者逐步将其应用到交通数据填补领域。例如，LI等[7]、王力等[8]和张润生等[9]基于生成对抗网络在数据填补领域的优越性能，将路网交通流量数据的时空特性融合进生成对抗网络中，实现对路网中缺失流量数据的高质量填补。

综上，已有学者围绕交通事故数据填补和生成对抗网络展开研究，但针对生成对抗网络在交通事故数据填补中的研究和应用均较为缺乏。生成对抗网络作为一种强大的深度学习工具，能够准确捕捉原始数据的复杂分布，特别适合处理高维、非线性和复杂的数据结构，更好地模拟真实数据的分布，从而提高填补的准确性。此外，生成对抗网络适用于所有类型的缺失机制，包括完全随机缺失、部分随机缺失和非随机缺失等，其在实际应用中普适性更强。鉴于此，拟针对追尾事故数据中的数据缺失问题，构建针对性的生成对抗网络，高质量完成训练数据填补，形成完备的训练事故数据集。在此基础上，构建LightGBM 模型，使用未经填补的测试数据检验数据填补对模型预测精度的影响。相关成果对完善事故严重程度预测理论、改善交通安全有一定参考价值。

1 数据描述

1.1 数据来源及预处理

考虑事故数据获取难易程度及原始事故数据质量问题，选取芝加哥交通事故数据集作为数据来源，筛选出2016—2021年涉及两车相撞的101452条追尾事故数据进行分析。对事故无关变量剔除后，得到20 项事故自变量，涉及驾驶人、车辆、道路及环境信息等。将事故严重程度等级定义为事故因变量，将其划分为无受伤事故、轻伤事故、重伤或死亡事故这3类。其中，无受伤事故共96043起，轻伤事故共4678起，重伤或死亡事故共731起。

1.2 数据编码

因原始数据中事故变量分类繁多，不利于后续建模分析，在建模分析前对其进行细化分类并编码。因事故涉及两方车辆，根据车辆碰撞位置区分前后车辆，其中车辆1为前车，对应驾驶人1；车辆2为后车，对应驾驶人2。具体变量定义及编码如表1所示。

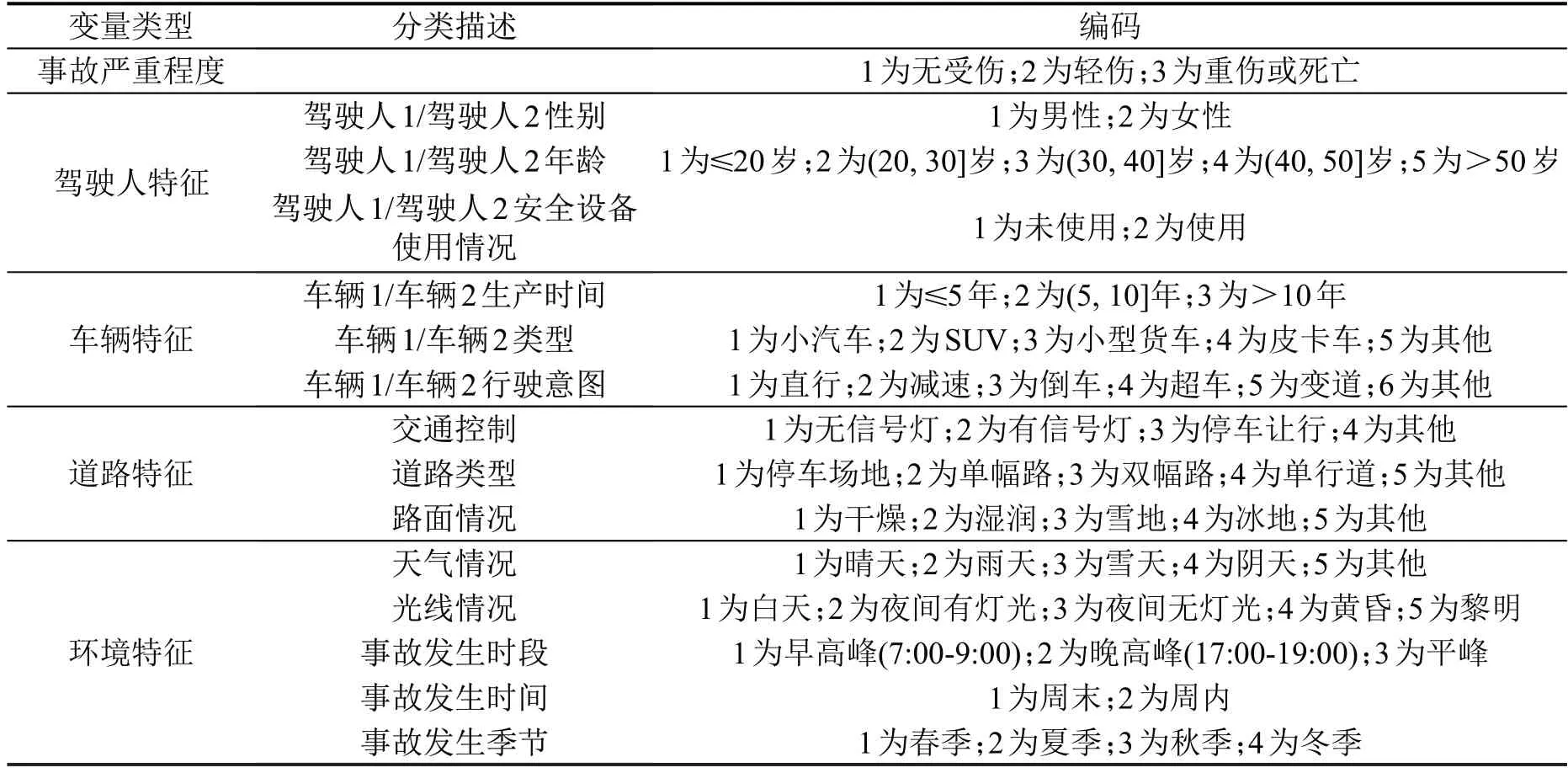
表1 变量定义及编码Table 1 Variable definition and coding

2 数据填补

2.1 数据缺失情况分析

统计数据缺失情况可知，事故严重程度作为因变量，无缺失值存在；事故自变量中除事故发生时段、事故发生时间、事故发生季节外，共有17 个因素存在缺失值，具体情况如表2所示。

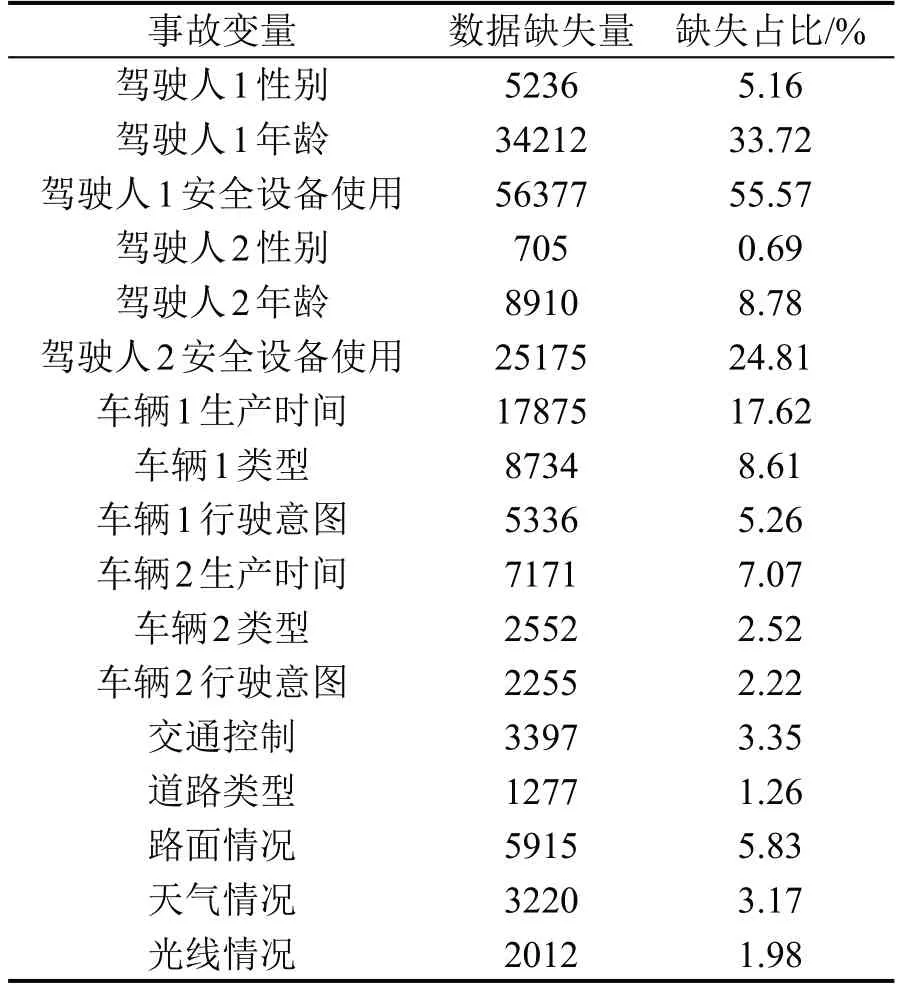
表2 数据缺失情况统计表Table 2 Data missing statistics table

2.2 生成式插补网络算法

作为基于GAN 的衍生算法，GAIN(Generative Adversarial Imputation Nets)的提出为缺失数据的插补提供了新思路[10]。作为一种无监督插补方法，GAIN 适用于所有类型的缺失机制，包括完全随机缺失、部分随机缺失和非随机缺失等。GAIN 的核心思想是利用生成对抗网络来模拟和学习数据的底层分布，从而更准确地估计和插补缺失的数据。

GAIN 主要由两个深度神经网络构成：生成器G和判别器D。生成器负责根据已知数据生成缺失数据，而判别器则尝试区分一个给定的数据点是真实数据还是插补的人工数据。

假设X是原始数据矩阵，其中部分数据(例如xij)为缺失值。定义M为与X同样大小的二进制掩码矩阵，用于表示某个数据是否缺失：若xij为缺失数据，则mij=0；否则，mij=1。同时，定义Z为与X同样大小的随机噪声矩阵，用于辅助生成器生成插补数据；对二进制掩码矩阵M进行模糊化处理，生成提示矩阵H，具体而言，M中的1(表示数据是完整的)有一定概率被设置为0.5，而M中的0(表示数据缺失)同样有一定概率被设置为0.5。模糊化处理后的提示矩阵H提供了关于数据完整性的部分信息，这强化了生成器和判别器的对抗训练过程，使整个模型生成的插补数据质量更高，且训练过程更加稳定。

生成器试图基于原始数据矩阵X、掩码矩阵M和随机噪声矩阵Z，估计缺失数据的值，并输出完整的数据矩阵，即

式中：G为生成器函数，它是一个全连接的多层前馈神经网络，用于学习原始数据的分布并生成缺失的值。生成器的隐藏层通常使用ReLU(Rectified Linear Unit)激活函数，其输出层通常使用Softmax激活函数。

判别器接收生成器的输出和提示矩阵H作为输入，试图判断数据矩阵中的每个值是真实数据还是生成器生成的填补数据，并计算每个值是真实数据的概率，即

式中：D为判别器函数，也是一个全连接的多层前馈神经网络，用于区分真实数据和生成器生成的人工数据。判别器的隐藏层通常使用ReLU 激活函数，其输出层通常使用Sigmoid激活函数。

在GAIN 中，使用两种损失函数来分别训练生成器和判别器。其中，判别器的损失函数为

生成器的损失函数为

式中：E为数学期望。

在GAIN的训练过程中，生成器G尝试最小化该目标函数，判别器D尝试最大化该目标函数。在对抗训练过程中，两者逐步达成纳什均衡，此时判别器D无法识别输入的数据是真实数据还是生成器G生成的人工插补数据，训练完成。具体计算步骤如下。

①定义迭代次数T。

②随机初始化生成器和判别器的参数。

③从原始数据集X中随机选取一个批次的数据Xbatch。

④根据Xbatch生成对应的掩码矩阵Mbatch、随机噪声矩阵Zbatch和提示矩阵Hbatch。

⑤使用生成器G生成插补数据batch=G(Xbatch,Zbatch,Mbatch)。

⑥固定生成器参数，基于batch和Hbatch优化判别器损失函数LD，更新判别器参数。

⑦固定判别器参数，优化生成器损失函数LG，更新生成器参数。

⑧重复步骤③～步骤⑦，直至遍历所有数据，完成1次迭代。完成所有T次迭代后，整个模型训练完成，输出最终的插补数据矩阵。

2.3 算法对比

现有的数据填补方法基本上可分为统计学方法和机器学习方法两类[11]，前者是利用原始数据集做出假设，然后对缺失值进行填补；后者大多是在对缺失数据进行分类或聚类的基础上进行填补。为更加全面地验证GAIN的数据填补效果，选取统计学填补方法中的MICE 填补算法和EM 填补算法，机器学习填补方法中的MissForest 填补算法和KNN填补算法作为对比。选取自变量方差作为对比指标，计算公式为

式中：σ2为方差；xi为第i个变量；μ为样本均值；N为样本大小。

保持相同的运行环境，17个含缺失值的自变量在经过不同算法填补后的方差如表3所示。

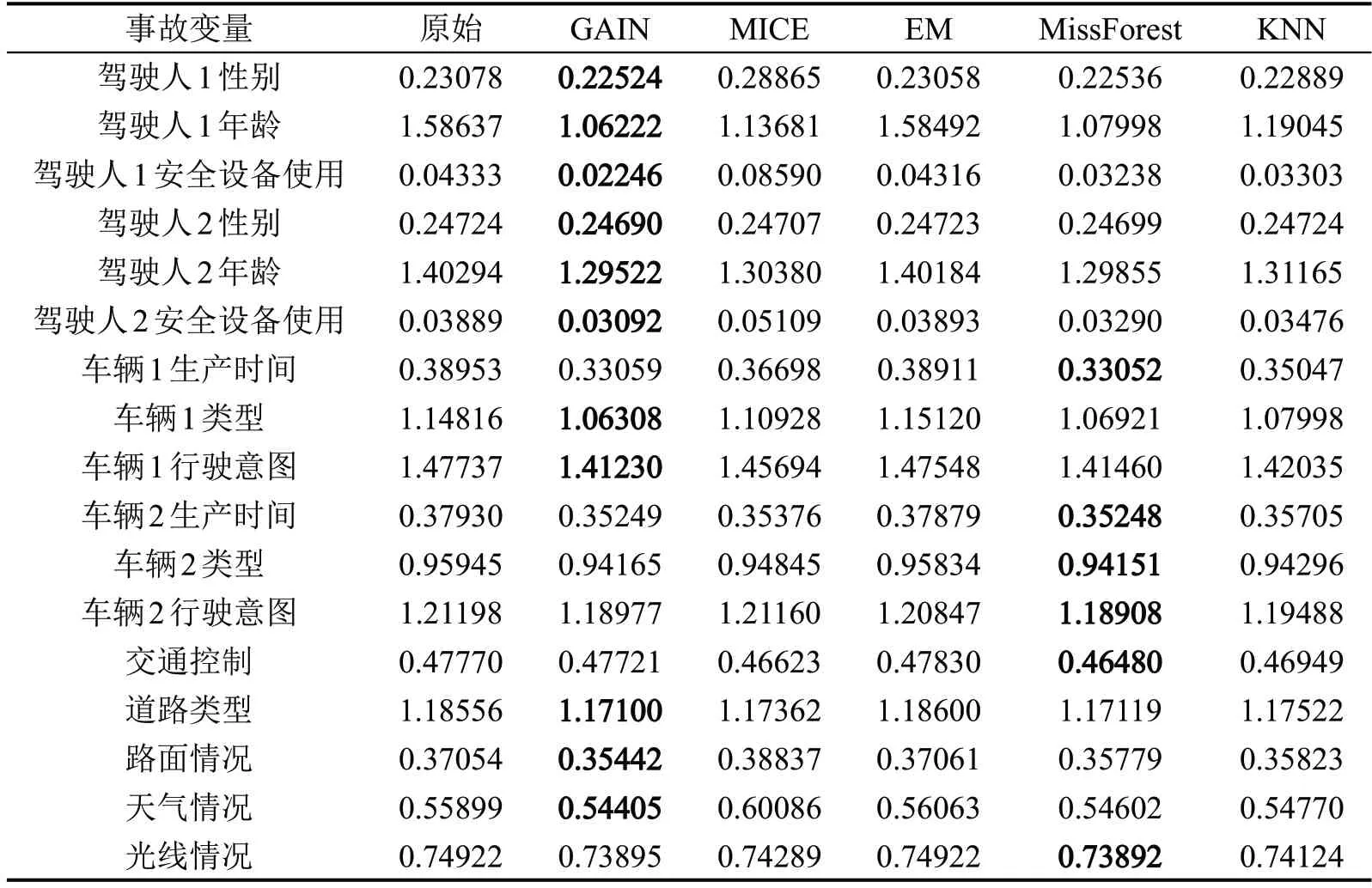
表3 自变量方差对比表Table 3 Comparison of variances of independent variables

在缺失值的填补过程中，填补的值往往是根据数据中已有的信息计算得到的。如果填补后的数据方差变小，则说明填补后的数据相对于原始数据来说更加稳定，变异性减小。由表3 可以看出，在17 个自变量的方差结果中，有11 个自变量的方差在经由GAIN 算法填补后达到最小，有6 个自变量的方差经由MissForest 算法填补后达到最小，从统计学意义上证明了使用GAIN 算法填补数据可以使数据更加稳定。

但仅依靠填补前后方差变化判断填补效果不够全面，有一定局限性。数据填补的最终目的仍是为下游的机器学习模型服务。因此，数据填补对模型预测效果的改善是评估填补效果更为重要的指标。

3 模型构建

在完成数据填补后，进一步建立事故严重程度预测模型，将事故严重程度作为因变量，驾驶人特征、车辆特征、道路特征和环境特征等作为自变量进行建模分析。首先，将原始数据按照7∶3随机分为训练集和测试集。对训练集数据使用不同数据填补算法完成数据填补，并使用不同算法填补后的训练集数据，以及未经填补的原始训练集数据分别训练LightGBM(Light Gradient Boosting Machine Method)模型。然后，使用未经填补的测试集数据测试模型预测效果，以全面、客观地评估不同数据填补算法对模型预测性能的改善。

3.1 模型基本原理

LightGBM 是针对梯度提升决策树(Gradient Boosting Decision Tree,GBDT)的一种改进方法[12]，LightGBM 模型能够在保证精度的同时，有效提高数据处理效率。LightGBM 在模型训练过程中，选择最大损失的叶生长，当生长相同叶的时候，通过竖向和横向相比来减小损失并加快运算速度。LightGBM 为减少特征数量和样本数量、提高算法计算效率，使用了单边梯度采样(Gradient based One-Side Sampling,GOSS) 和互斥特征绑定(Exclusive Feature Bundling,EFB)技术。GOSS 以信息增益为判断规则，排除对计算信息增益无帮助的小梯度样本，保留对信息增益影响更大的大梯度样本。EFB 基于高维数据在稀疏的特征空间互相排斥的思想，提出通过绑定互斥特征来减少特征数量。基于此，LightGBM 算法能够有效降低训练任务的计算复杂度，同时能够提高计算速度和减少内存，综合表现优于其他GBDT算法。

基于Python3.9构建LightGBM模型，将各子集的最小样本量设置为20，学习率设置为0.1，树的最大深度设置为1，总迭代次数设置为1000。

3.2 模型结果对比

为充分评估模型预测结果，选择准确率(Accuracy)、F1 和AUC 作为模型评价指标，对模型结果进行对比分析。

(1)准确率

准确率指正确预测的样本数占总样本数的比例，计算公式为

式中：ETP为真正例；ETN为真负例；EFP为假正例；EFN为假负例。准确率越高，说明模型预测效果越好。

(2)F1

F1 是精确率(Precision)和召回率(Recall)的调和平均值，计算公式为

式中：PPrecision为精确率值，PPrecision=ETPk (ETP+EFP)；RRecall为召回率值，RRecall=ETP/ (ETP+EFN)。通常情况下，F1值越高，说明模型预测效果越好。

(3)AUC

AUC是ROC(Receiver Operating Characteristic)曲线下的面积，ROC 曲线是在不同分类阈值下，真正例率(ETP/ (ETP+EFN))与假正例率(EFP/ (EFP+ETN))之间的关系图。AUC 提供了一个模型性能的整体评价，其值在0.5～1.0 之间，越接近1.0，说明模型的预测效果越好。模型评价指标的具体结果如表4所示。

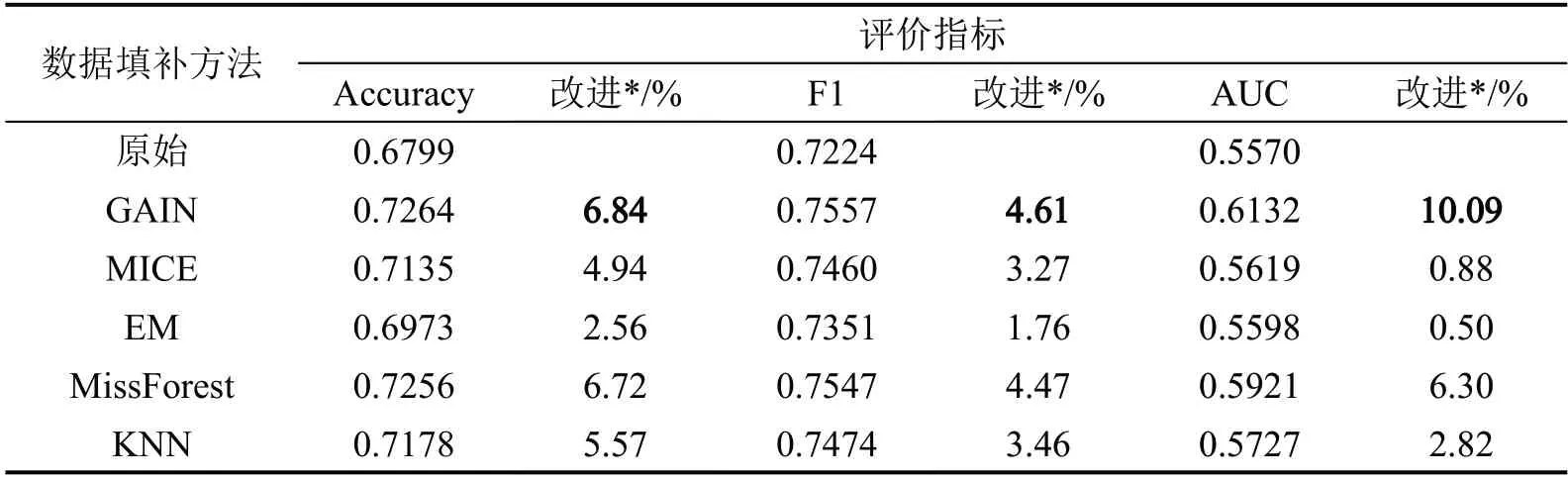
表4 模型评价指标对比Table 4 Comparison of model evaluation indicators

由表4可知，使用原始数据训练的模型指标最差。利用上述5 种算法对原始数据集中的缺失值进行填补后，模型指标均得到了一定改善。其中，GAIN 算法填补后的数据训练的模型指标最优，对比原始数据训练的模型，准确率提高了6.84%，F1提高了4.61%，AUC 提高了10.09%。这说明，针对该事故数据集，GAIN 算法的填补效果优于其他4 种填补方法，能够在一定程度上改善模型的预测结果。

4 结论

(1)细化研究各变量的数据缺失率，采用GAIN算法，统计学中的MICE算法和EM算法，以及机器学习中的MissForest 算法和KNN 算法对追尾事故数据中的缺失值进行填补，并对比填补前后各变量的方差变化，在含缺失值的17个自变量中，有11个变量经由GAIN算法填补后结果最优。

(2)构建三分类LightGBM 事故严重程度预测模型，对原始数据集和填补后的各数据集进行建模分析，从模型预测结果角度对比分析各填补方法的优劣。对比模型评价指标准确率(Accuracy)、F1 和AUC 可知，使用GAIN 填补后的数据集训练模型，相较于使用原始数据训练模型，其模型准确率提高了6.84%，F1提高了4.61%，AUC提高了10.09%，并优于其他4种填补方法。