面向动态交通分配的交通需求深度学习预测方法

李岩，王泰州，徐金华，陈姜会，汪帆*,2

(1.长安大学，运输工程学院，西安 710064；2.中交第一公路勘察设计研究院有限公司，西安 710075)

0 引言

在交通管控系统层级的改善效果评估等工作中，需精确描述各时段路径流量和路径出行时间的相互作用关系，以获得精准的交通运行状态。传统的静态交通分配方法仅能获取相对较长时段的交通分析结果，加之出行者完成出行需要时间，使静态分配难以分析各时段交通状态变化特征。为获取网络全过程的交通运行状态分析结果，需应用动态交通分配(Dynamic Traffic Assignment,DTA)[1]。动态交通分配需预先输入各分析子时段的交通需求，而传统预测方法多基于历史数据和经验，忽略了动态交通分配过程中交通需求时间序列数据的周期性、随机性和非线性等特点[2]，无法响应动态交通分配所需输入的数据要求。因此，亟需建立一种面向动态交通分配的交通需求预测方法。

目前，面向动态交通分配的交通需求预测方法[3]可以总结为基于统计分析、机器学习以及深度学习等3 类。基于统计分析预测方法的主要模型有自回归积分移动平均(Auto Regressive Integrated Moving Average,ARIMA)模型、卡尔曼滤波模型等。ARIMA[4]模型将交通流量视为非平稳随机序列处理，其对平滑性较强的数据预测效果更好，但对随机性更强，存在极端峰值的数据预测效果欠佳。卡尔曼滤波算法[5]允许所选状态变量不断更新，根据某些反映历史交通需求变化的规律性数据对未来需求的变化进行推断以实现预测，但随着数据非线性或不稳定特征增加而使预测精度下降。由于动态交通分配中的交通需求是非线性、非平稳的复杂时间序列数据，基于机器学习的方法能够克服统计分析模型的约束，从而处理更加复杂的交通需求数据，主要的模型有支持向量机模型(Support Vector Machine,SVM)、K 最近邻算法(K Nearest Neighbor,KNN)等。SVM模型[6]能够处理非线性数据，具有较强的泛化能力，但其具有参数的敏感性、计算复杂度高等不足。KNN 算法[7]可以处理更加复杂的交通需求数据，相比与支持向量机模型的训练时间复杂度较低，但其对于面向DTA 的交通需求预测任务中复杂时间特征的捕捉有待进一步优化。相比于机器学习的模型，基于神经网络的深度学习预测方法可以更好地处理交通需求预测中时空特征的非线性和动态性、出行需求的随机性与规律性等问题。但不同的神经网络模型其预测性能也存在一定的差异，如堆叠自编码神经网络(Stacked Auto Encoding neural network,SAE)[8]，此类模型基于全连接神经网络，难以有效表征交通信息中蕴含的特征，模型表示能力有限。考虑到上述局限，从时序特征角度引入长短期记忆网络(Long Short-Term Memory,LSTM)[9]，在交通需求的长期与短期预测中表现出对历史信息的优秀整合能力。但是，神经网络模型需根据经验选取训练次数、学习率及隐藏层神经元个数等，使模型训练耗时长、容易过拟合且降低了预测精度。为此，引入遗传算法(Genetic Algorithm,GA)、粒子群算法(Particle Swarm Optimization,PSO)、灰狼算法(Grey Wolf Optimization,GWO)等参数寻优算法对其关键参数进行优化，以提高神经网络模型的预测性能。GA 算法[10]具有良好的全局搜索能力，但其参数较多，寻优时间相对较长。PSO算法[11]相较于GA 算法，其没有交叉与变异操作，参数较少，但容易陷入局部最优解，且对参数的调节比较敏感。GWO 算法[12]能够快速地找到全局最优解，而且收敛速度比较快，但在处理高维度问题时容易陷入局部最优解。而布谷鸟寻优算法(Cuckoo Search,CS)[13]与GA 算法、PSO 算法等算法相比，具有参数少、易实现、搜索路径优、寻优能力强的特点。

综上所述，为进一步在运行效率、模型结构、预测精度等方面优化面向动态交通分配的交通需求预测方法，从动态交通分配的角度出发，基于视频监控获取的车牌数据构建了一种面向动态交通分配交通需求的深度学习预测方法，以满足动态交通分配研究对反映交通时变特征的交通需求的需求。

1 研究思路及框架

DTA需要以一定时间粒度划分交通需求，并将相应时段的交通需求加载到路网中，因此在预测面向DTA 的交通需求时，选取对复杂交通需求时间序列数据响应性能好的方法，考虑到LSTM对交通需求等时间序列数据具有良好的预测效果，由此以LSTM 为基础构建面向DTA 的交通需求预测方法。考虑到DTA连续分时段的交通需求数据的时序特征，引入时间序列分解方法(Seasonal and Trend decomposition using Loess,STL)将交通需求数据分解为周期分量、趋势分量和余项分量，从而减少数据噪声以及异常值的影响。其中，STL分解得到的周期分量在各个周期内是相同的[14]，因此采用周期估计的方法进行预测，即预测时段的周期分量值选取原始交通需求数据STL 分解得到的对应周期分量。针对LSTM易受超参数影响的问题，选取具有随机寻优能力较强、寻优效率高等特征的CS 算法对预测方法进一步优化，从而使所预测的交通需求满足DTA 对需求数据在准确性、时效性等方面的要求。综上确定整体研究框架如图1所示。

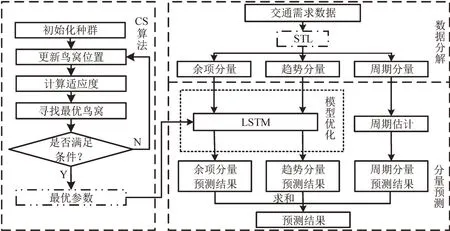
图1 研究整体框架图Fig.1 Overall framework of research

2 面向动态交通分配的交通需求预测方法

2.1 基于局部加权回归的周期趋势分解

STL 方法是一种以鲁棒局部加权回归作为平滑方法的数据分解方法，可分解交通需求等时间序列数据。对于交通需求数据，截取其所在样本的数据区间，使用加权最小二乘法进行回归分析，使估计点附近的值拥有相对较大的权重，以获得局部回归模型；重复此过程，直到获得回归曲线。STL 方法基于鲁棒局部加权回归(Locally Weighted Regression,LOESS)将原始交通需求数据Yt分解为t时刻的趋势分量Tt、周期分量St和余项分量Rt。其模型分解算法的计算式为

式中：N为交通需求数据的时间序数。

2.2 布谷鸟寻优算法

CS算法是一种基于自然界布谷鸟寄生种群策略的启发式算法，通过模拟布谷鸟巢寄生性和Levy 飞行以在空间上随机移动的方式寻优出最优解的寻优模式。CS 算法的全局搜索能力强，收敛速度快，参数设置相对简单，易于实现和应用于LSTM模型参数优化问题的求解。

布谷鸟寻找宿主鸟巢的位置和路径更新公式为

式中：为第p个鸟巢在第q次迭代时的位置；n为鸟巢个数，即可行解个数；λ为搜索数；α为步长缩放因子，α>0，且服从正态分布；⊗为点对点乘积；L(λ) 为 Levy 随机搜索路径，且Levy ∼u=t-λ,1<λ≤3，其中，u为由Levy飞行得到的随机步长。

2.3 长短期记忆神经网络

LSTM 神经网络是循环神经网络(Recurrent Neural Network,RNN)的一种，可以解决长时间序列训练时出现的梯度爆炸和消失问题，有效提取长时间序列中的信息，更适合处理交通需求等时间序列数据。LSTM 相比于RNN，增加记忆单元，包含遗忘门、更新门和输出门，可以利用历史信息，网络结构如图2所示。

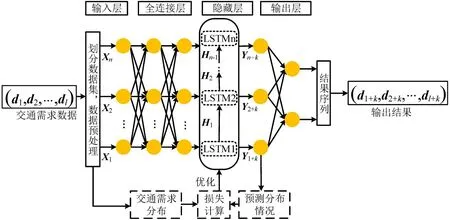
图2 LSTM网络结构Fig.2 Network structure of LSTM

图2 中，(X1,X2,…,Xm)表示任意OD 点的输入序列，(Y1,Y2,…,Ym)表示任意OD 点的输出序列，(H1,H2,…,Hm)表示隐藏层状态，(d1,d2,…,dl)表示输入交通需求数据，m表示路网的起讫点数量，l表示输入数据的时间序数；(d1+k,d2+k,…,dl+k)表示输出交通需求预测结果，k表示预测时间步长。交通需求数据在时间序数为t时的矩阵dt为

2.4 构建CS算法优化的LSTM模型

CS算法改进LSTM模型的具体步骤如下。

Step 1 初始化神经网络的超参数，确定迭代次数、学习速率、隐藏层单元数量变化区间。

Step 2 初始化CS 算法参数，随机生成鸟巢的位置，每个鸟巢的位置包含4个参数(LSTM第1层、第2层隐藏层单元数量L1、L2，学习速率Lr和训练迭代次数K)。根据鸟巢初始化的各个参数进行训练，计算每个鸟巢的预测值，找到误差最小的鸟巢位置，保存到下一代。

Step 3 根据鸟巢位置和路径更新式(2)进行更新，通过LSTM 神经网络计算预测误差，与Step 2中除最小鸟巢之外的其他鸟巢进行对比，得出误差最小的鸟巢替代误差最大的鸟巢，从而得到当前的最优鸟巢位置。

Step 4 得到最优鸟巢，即可得出超参数的最优组合。若达到精度要求，则返回上一步继续搜索；否则，输出当前最优值。

Step 5 在每一次迭代之后，有一部分鸟巢按照丢弃概率被抛弃，使得该搜索算法可以获得最佳适应度值。

Step 6 在神经网络模型中输入训练数据进行训练，若未达到预测精度或超出迭代范围，则不断学习；若达到迭代次数或预测精度，则停止神经网络的学习，保存当前最优超参数组合。

3 实例分析

3.1 实验数据及研究区域

应用西安市长安区部分路网2021年3月8日—4月4日视频卡口的车牌数据验证所提出方法。数据记录了设备编码及通过卡口车辆的车牌、车道、行驶方向、车速、时间等信息。由于采集设备均设在交叉口范围内，故选取交叉口节点作为交通小区。基于车牌数据通过追踪每个车辆的行驶轨迹，确定车辆出行的起讫点，由此获取路网交通需求数据。研究区域共有检测器节点33 个，无检测器节点14个，路段75个，研究区域路网及节点分布情况如图3所示。

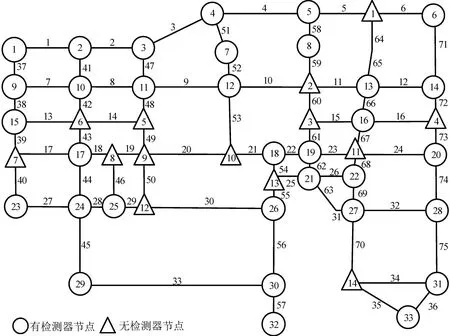
图3 研究区域路网布局图Fig.3 Layout of road network in studied area

3.2 评价指标

为验证预测方法的有效性和实验结果的准确性，利用常用统计指标对实验误差进行评价，选取平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)和决定系数(Coefficient of Determination,R2)作为评价指标量化预测结果。3个评价指标的表达式分别为

式中：ERMSE为RMSE的值；EMAE为MAE的值；和yt分别为交通需求的预测值和实际值。

3.3 时间间隔选择

根据DTA 分析精度等要求，其对交通需求数据集的时间间隔要求也有所差异，因此需对所获取交通需求数据集的时间粒度进行分析。因动态交通分配研究时长一般为1～2 h，对应交通需求数据的统计时间间隔为5～20 min，因此确定时间间隔为5，10，15，20 min。取研究时长为1 h，对应时间序列阶数分别为12、6、4、3。为选取最优时间间隔，以均方根误差为指标分析各时间间隔的交通需求预测结果，对各时间间隔下阶数进行统计，考虑到数据基数的倍数差异，以均方根误差最小为准则得到相应误差，结果如表1所示。

表1 不同时间间隔下最优时间序列阶数统计Table 1 Statistical results of optimal time series orders at various time intervals

当等效时长当60 min时，15 min时间间隔时的均方根误差最小。因此，综合考虑交通需求预测误差以及网络预测效率等因素，针对测试路网选取15 min时间间隔。

3.4 STL数据分解结果

设置预测步长为4，即根据历史每1 h的交通需求预测后续15 min的交通需求；同时考虑交通需求数据以24 h为单位的周期特征，设置STL的周期参数为96。周内各工作日的交通需求时序特征也存在一定差异，因此选取2021 年3 月29 日—4 月4 日共5 个工作日的交通需求数据作为测试集，STL 分解的结果如图4所示。

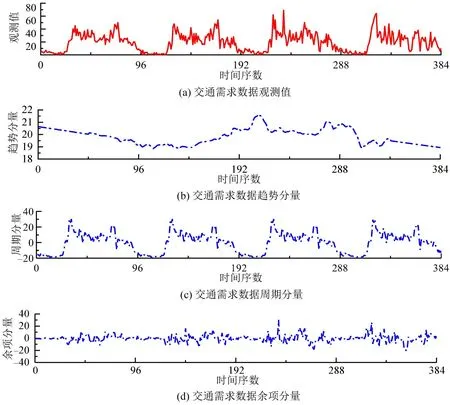
图4 交通需求数据STL分解结果Fig.4 Decomposition results of traffic demand data using STL

从图4可以看出，交通需求数据的趋势分量反映了剔除周期分量和余项分量后交通需求长期变动的真实趋势，即交通需求数据长期变化的波动性，其变化曲线平滑且在18.5～21.5范围内波动；周期分量呈现了交通需求数据早晚高峰及日间平峰的周期性变化特征；余项分量体现了交通需求数据的随机性特征，随机性被包含在有序周期内，在-24～32范围内波动。

3.5 不同研究时段的预测结果

对不同研究时段交通需求预测模型的结果误差进行评价。在预测性能的比较中，对单一LSTM、支持向量回归(Support Vector Regression,SVR)和自回归滑动平均(Auto Regressive Moving Average,ARMA)模型的预测效果进行统计。单一LSTM模型的参数设置与STL-CS-LSTM预测模型相同，模型初始参数(L1,L2,Lr,K)的范围设置为([1,100],[1,100],[0.001,0.01],[10,100])。根据交通需求数据绘制的自相关函数曲线图、偏相关函数曲线，并根据赤池信息准则确定ARMA 最优模型为ARMA(2,1)。SVR 预测精度的参数主要为惩罚系数C和高斯核函数幅宽g，交通需求预测参数(C,g)设置为(10.00,0.05)。STL-CS-LSTM 模型与其他3 种预测模型在早晚高峰(7:00-9:00,18:00-20:00)、日间平峰(9:00-18:00)时段和全日(7:00-20:00)时段的所有起讫点交通需求数据的模型预测效果评价指标结果如表2所示。

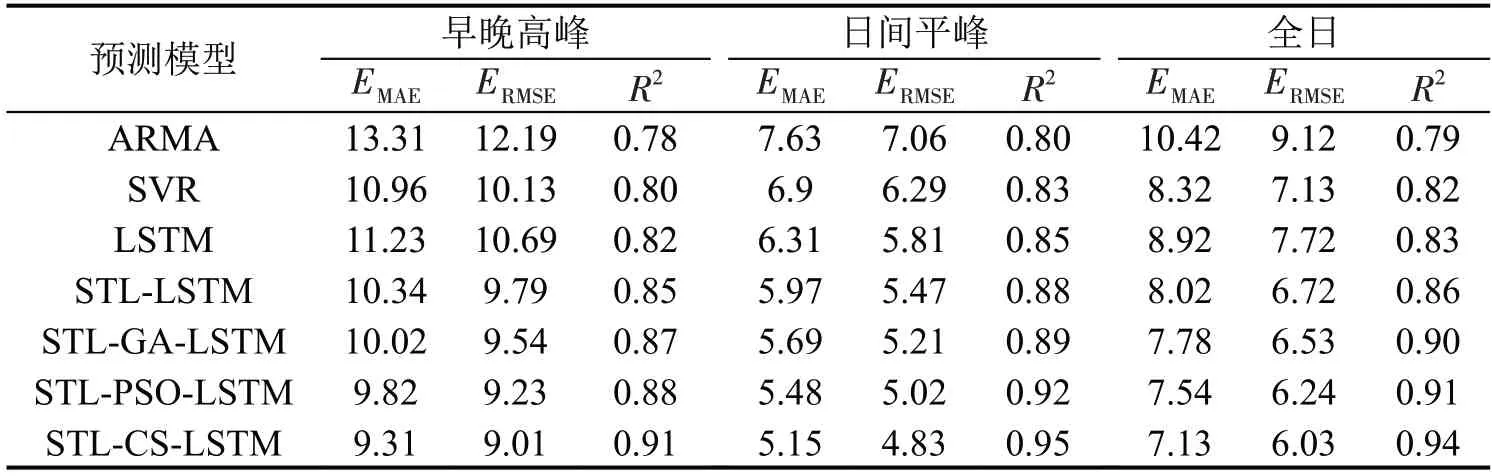
表2 不同时段模型预测结果Table 2 Prediction results of proposed model at various time periods

从表2 结果可知，在3 个不同的连续时段(高峰、平峰、全日)，面向动态交通分配的交通需求预测中，STL-CS-LSTM预测模型比LSTM模型、SVR模型、ARMA 模型的决定系数R2增加了10.83%～15.04%，均方根误差ERMSE以及绝对平均误差EMAE分别降低了11.06%～17.88%、14.30%～18.50%，说明所提出的STL-CS-LSTM模型在不同时段(高峰、平峰、全日)都能取得良好的预测结果。将STLLSTM模型与单一LSTM模型对比，其ERMSE、EMAE分别降低了10.09%、12.95%，决定系数R2增加了3.61%，说明STL 分解算法可以提高LSTM 模型的预测精度。同时将本文所提出的CS算法优化的模型与GA、PSO算法优化的模型相比，ERMSE、EMAE分别降低了5.44%～8.35%、3.37%～7.66%，决定系数R2增加了3.30%～9.30%，说明CS 算法相比于GA、PSO 等算法在提高LSTM 交通需求预测模型预测精度方面具有优势。

动态交通分配研究需要高精度的连续时段的交通需求数据，因此分别选取高峰和平峰两个时段连续4个时间间隔进行交通需求预测，其评价结果如表3～表6所示。

表3 高峰连续时间间隔模型预测结果Table 3 Prediction results for consecutive periods at peak hours

表3 和表4 为STL-CS-LSTM 模型与LSTM 模型、SVR 模型、ARMA 模型在高峰和平峰两个时段连续4 个时间间隔交通需求预测误差评价指标计算结果。STL-CS-LSTM 模型的预测结果相比于LSTM模型、SVR模型、ARMA模型，高峰时段(8:00-9:00)的决定系数R2增加了8.62%～11.74%，均方根误差ERMSE以及绝对平均误差EMAE分别降低了11.20%～17.99%、12.33%～18.86%；平峰时段(14:00-15:00)的决定系数R2增加了9.56%～12.48%，均方根误差ERMSE以及绝对平均误差EMAE分别降低了11.83%～17.97%、10.55%～19.80%。

表4 日间平峰连续时间间隔模型预测结果Table 4 Prediction results for consecutive periods at off peak hours

表5和表6 为STL-CS-LSTM 模型与STLLSTM模型、STL-GA-LSTM模型、STL-PSO-LSTM模型在高峰和平峰两个时段连续4 个时间间隔交通需求预测误差评价指标计算结果。STL-CSLSTM 模型的预测结果相比于其他3 种模型，高峰时段(8:00-9:00)的决定系数R2增加了8.62%～11.74%，均方根误差ERMSE以及绝对平均误差EMAE分别降低了11.20%～17.99%、12.33%～18.86%；平峰时段(14:00-15:00)的决定系数R2增加了9.56%～12.48%，均方根误差ERMSE以及绝对平均误差EMAE分别降低了11.83%～17.97%、10.55%～19.80%。

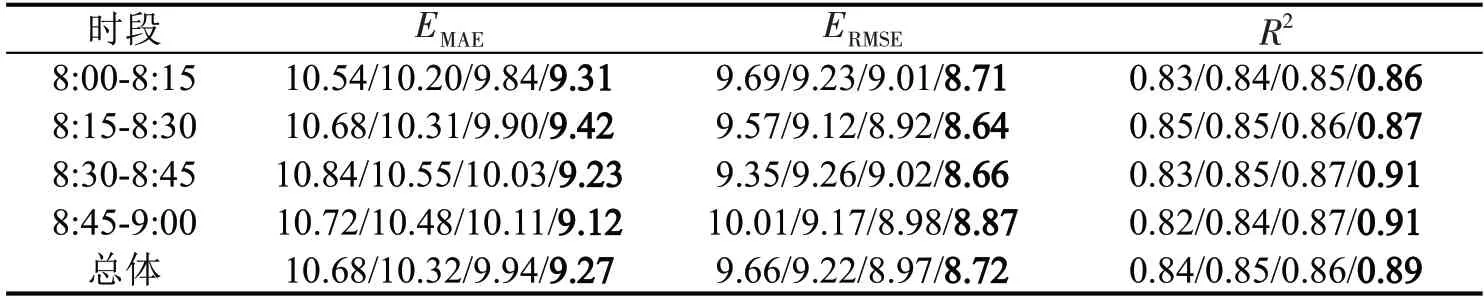
表5 高峰时段不同算法优化的模型预测结果Table 5 Prediction results optimized by different algorithms at peak hours

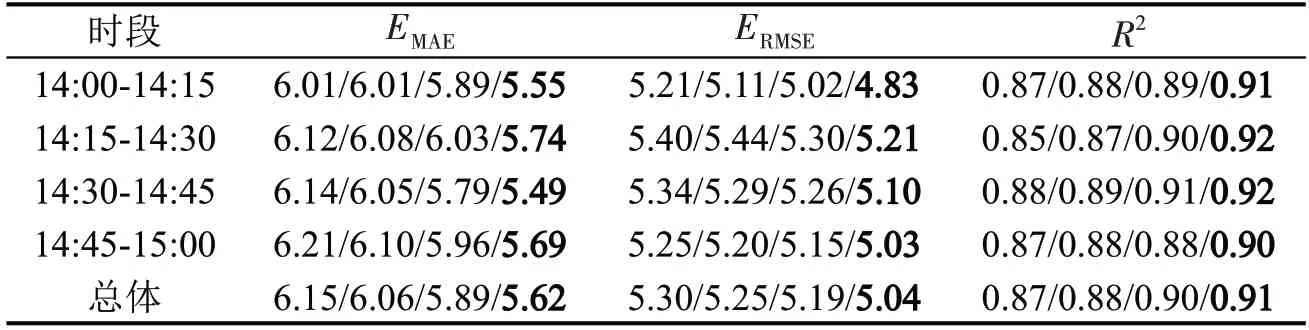
表6 日间平峰时段不同算法优化的模型预测结果Table 6 Prediction results optimized by different algorithms at off peak hours

同时，根据表3～表6 可以看出，STL-CS-LSTM模型无论是高峰还是平峰时段连续时间间隔内都能取得良好的预测结果。

3.6 全日预测结果分析

通过对研究区域内全日运用STL-CS-LSTM模型进行预测，以体现STL-CS-LSTM 模型在全日所有时段的预测效果。STL-CS-LSTM的全日交通需求预测方法的以1-2起讫点为例的预测结果如图5所示，并同LSTM 模型，SVR 模型和ARMA 模型的预测结果对比。

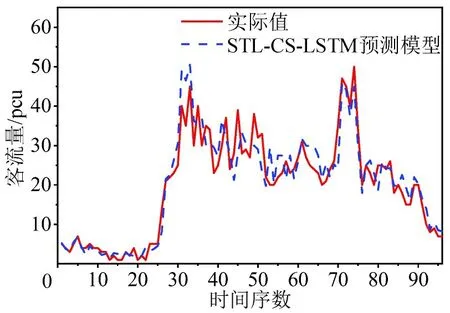
图5 STL-CS-LSTM模型预测结果Fig.5 Prediction results of STL-CS-LSTM model

利用EMAE、ERMSE和R2量化预测结果，不同模型的预测评价指标结果如表7所示。

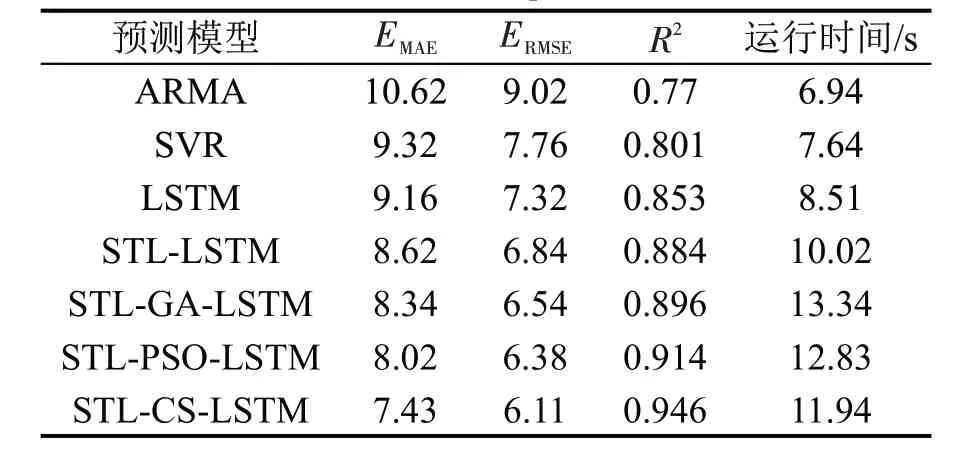
表7 不同模型评价指标结果对比Table 7 Prediction results comparison of various models

从图5 可以看出，STL-CS-LSTM 模型的预测结果可以对交通需求的变化趋势进行很好地拟合，说明全日所有时段的预测效果良好。从表7 可以看出，STL-CS-LSTM模型具有更好的预测精度，其预测结果的误差值均小于其他3种预测模型，决定系数均高于其他3种模型。相比于SVR、ARMA等预测模型，LSTM预测模型其EMAE和ERMSE指标分别降低了11.92%、13.56%，R2提高了8.64%，预测精度得到提高；引入STL 方法以及CS 优化算法的STL-CS-LSTM模型，相较于LSTM模型，EMAE和ERMSE指标分别降低了11.89%、12.53%，R2提高了7.90%，预测精度有了进一步的提高，表明在全日所有研究时段内相比单一模型LSTM模型、SVR模型以及ARMA 模型，STL-CS-LSTM 模型的预测精度最高。同时，将STL-CS-LSTM 模型与STL-LSTM模型、STL-GA-LSTM 模型、STL-PSO-LSTM 模型对比，EMAE和ERMSE指标分别降低了7.36%～13.81%、4.23%～10.67%，R2提高了3.50%～7.01%，且本文所提出的模型运行时间最短，说明在全日所有时段的预测中，STL-CS-LSTM 预测模型具有最优的预测精度及运行效率。

面向动态交通分配的STL-CS-LSTM交通需求预测方法，通过算法对样本的训练与学习，能够映射并处理交通量随时间变化的复杂非线性规律，基于STL方法和CS算法可以有效提高LSTM的预测性能，实现面向动态交通分配的较高精度的交通需求预测。

4 结论

本文得到的主要结论如下：

(1) 面向动态交通分配需求构建了STL-CSLSTM交通需求预测方法，应用区域视频监控卡口的车牌数据，根据DTA 对交通需求数据精度等要求，针对测试路网以15 min统计交通需求数据。

(2)应用西安市长安区数据测试结果表明，对比STL-CS-LSTM 模型与LSTM、SVR、ARMA、STL-LSTM、STL-GA-LSTM、STL-PSO-LSTM 模型，这7 种预测模型在早晚高峰、日间平峰和总体这3 个不同时段以及面向DTA 的4 个连续时段的预测效果中，STL-CS-LSTM 模型的预测效果均最优；对比同一起讫点的全日预测结果，相比于STLLSTM模型、STL-GA-LSTM模型、STL-PSO-LSTM模型，STL-CS-LSTM 模型预测结果的EMAE、ERMSE分别降低了11.89%～20.04%、12.53%～18.26%，R2提升了7.90%～14.86%，且模型的运行时间最短。

本文目前仅以西安市长安区部分路网数据进行实例分析，未来将通过更大范围的路网数据对更长时间内的动态交通分配需求数据预测进行验证及优化。