基于IA-VMD的浮环密封声发射信号降噪与特征提取
2024-03-02丁俊华丁雪兴
张 帅, 丁俊华, 丁雪兴, 力 宁
(1.兰州理工大学 石油化工学院,兰州 730050; 2.中国航发湖南动力机械研究所,湖南 株洲 412002)
浮环密封属于流阻型非接触式动密封,是现代机械设备的关键基础零部件,在工业生产中发挥着极其重要的作用,广泛应用于石化、航空、航海以及核电等领域,其密封面运行状态与设备稳定性以及寿命直接关联,非接触式密封状态监测已经成为国内外研究的重点[1-2]。随着航空发动机运行参数(转速、压力)的不断提升,浮环密封失效的主要因素包括:在运行过程中因动压不足在径向产生孔柱面碰磨和浮环环向振动引起的端面摩擦。在浮环密封状态监测中,从原始信号中提取碰摩、摩擦等特征信息对提高设备安全运行以及健康评估具有重要的意义。
浮环密封的状态监测主要通过加速度传感器、电涡流传感器及声发射传感器等实现。声发射技术是一种非破坏性监测方法,它对滑动轴承和机械密封等旋转机械的摩擦学行为非常敏感[3],但是声发射在进行密封系统监测的同时,往往也采集了随机环境噪声、轴承、电机等固定噪声。因此,声发射信号降噪至关重要。机械密封声发射信号通常采用小波变换或经验模态分解方法进行处理。孙鑫晖等[4]利用声发射技术对液膜密封端面进行监测,提出奇异值分解和自适应变分模态分解(singular value decomposition-adaptive variational mode decomposition,SVD-AVMD)的信号降噪方法,有效过滤了背景噪声并最大程度保留有效信息;林志斌等[5]在处理机械密封金刚石涂层磨损过程的声发射信号时,采用经验小波变换和相对熵(kullback-lebler divergence,KLD)的降噪方法,该方法对不同工况下的密封磨损信号,具有更强的适应性和稳定性;Fan等[6]使用改进经验模态分解(masking signals empirical mode decomposition,MS-EMD),研究干气密封启停阶段的声发射信号,有效区分了干气密封运行的声发射信号和环境噪声;Medina-Arenas等[7]使用声发射技术,分析了机械密封故障条件下的运行情况,并获得密封干摩擦的特征频率。声发射信号具有频域宽泛、信号敏感的特点。传统的小波时频变换具有较大的偏差。经验模态分解的结果主要依赖极值点的查找方法和停止准则,极容易出现模态混叠现象。变分模态分解(variational mode decomposition,VMD)是一种完全非递归的变分模态分解模型,比经验模态分解(empirical mode decomposition,EMD)对噪声具有更强的鲁棒性。同时VMD在轴承特征提取方面的应用较为成熟。曹洁等[8]采用VMD分解滚动轴承振动信号,并结合BP神经网络对滚动轴承进行故障诊断,提高了故障诊断精度;张爽等[9]利用快速VMD提取到滚动轴承故障特征频率,提高VMD的计算效率;Kumar等[10]将VMD应用在滚动轴承故障诊断中,通过相关性分析选择适当的IMF,确定轴承故障特征频率。然而,VMD在浮环密封声发射信号特征提取领域鲜见报道。
VMD的分解效率主要依靠模态数量和惩罚因子等参数的选择[11],若仅用经验或者先验准则选择参数,就会导致分解结果不准确,降低VMD的分解效率,因此,要对VMD参数进行优化。目前针对VMD参数的优化算法主要有:粒子群[12]、遗传算法[13]、麻雀算法[14]、灰狼优化算法[15]、鲸鱼优化算法[16]、布谷鸟搜索[17]和蝙蝠算法[18]等。免疫算法是遗传算法的优化,是在免疫算法中引入了浓度调节机制,解决了遗传算法的早期收敛问题,避免了重复无效的工作,从而提高了算法效率。目前,免疫算法在VMD参数优化方面还未见报道。
笔者采用免疫算法优化VMD参数,并以相对熵作为噪声判定准则。通过仿真和试验验证,对浮环密封声发射信号进行降噪处理,并对降噪后的信号进行特征提取研究。
1 基本理论
1.1 变分模态分解算法
变分模态分解理论是Dragomiretskiy等[19]在2014年提出,其本质是通过迭代搜寻变分模型,将原始信号分解为K个时间序列uk(t),最终得到约束变分模型为
(1)
式中:K为分解模态数;uk为分解后的K个模态分量;ωk为分解后每个模态分量的中心频率;*为卷积运算;f为原始信号。
VMD算法通过引入二次惩罚因子α和拉格朗日算子式λ(t),将其转换为无约束变分问题,其表达式为
(2)


步骤2令n=n+1,k=1 ∶K。

(3)
步骤4对拉格朗日算子进行更新。
(4)
式中,τ是噪声容限参数,通常设置τ=0。
步骤5重复步骤2~步骤4,直到满足终止迭代条件。
(5)
式中,ε通常设置为1×10-6,详细内容请参考文献[20]的研究。
1.2 免疫算法
VMD算法虽然可以抑制模态分量混叠,但是算法分解模态数K和惩罚因子α的选取主要依靠经验,影响了信号分解效果。免疫算法是一种智能优化方法,旨在解决复杂的优化问题,它是一种模拟生物免疫系统运行机制的启发式算法,具有自适应性、随机性、全局收敛性等优点,广泛应用于算法优化、人工智能等领域[21]。免疫算法是在遗传算法的基础上加入了免疫算子,目的是防止种群退化。算法步骤为
步骤1随机生成初始种群,并计算个体亲和度、抗体浓度和激励度。亲和度是表示两个个体之间的相似度,通常以抗体向量之间的欧式距离进行计算
(6)
式中:xi和xj分别为第i和第j个抗体向量;xi,k和xj,k分别为抗体i和抗体j的第维;L为抗体向量的总位数;抗体浓度用来表征抗体种群的多样性好坏,定义为
(7)
式中:N为抗体个数;S(xi,xj)为抗体间的相似度,可表示为
(8)
式中,s为相似度阀值。抗体激励度是用来衡量抗体质量的好坏,通常利用抗体亲和度和抗体浓度共同决定,表达式为
sim(xi)=a·A(xi)-b·Den(xi)
(9)
式中:sim(xi)为抗体的激励度;a和b为计算参数。
步骤2将抗体按照激励度的大小进行排序,对激励度N/2前个个体进行免疫操作,包括克隆、变异和克隆抑制;最后计算免疫个体的亲和度、抗体浓度和激励度,计算方法见步骤1。
步骤3随机生成N/2个个体的新种群,并计算个体亲和度、抗体浓度和激励度;将步骤2中免疫种群和随机种群合并,按激励度排序,进行免疫迭代。
步骤4判断是否满足终止条件:若满足则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
1.3 IA-VMD结合KLD降噪原理
1.3.1 亲和度函数
IA优化VMD参数时,主要经过抗原识别、初始抗体产生、亲和度评价、抗体促进与抑制、遗传操作5个步骤,其中亲和度函数对优化结果起着至关重要的作用。亲和度高的抗体容易受到促进,传进下一代的概率更大,而亲和度小的就会受到抑制,导致种群净化单一。
熵值能够反映一个系统的无规则程度,熵值越大则系统的无规则性越高;相反,熵值越小则系统的规则性程度越弱。样本熵不受样本长度的影响,具有较强的抗干扰能力且计算简便[22]。本文以样本熵作为优化算法中的亲和度函数。样本熵的表达式为
(10)
式中:m为嵌入维数;r为相似容限;N为样本长度。
1.3.2 相对熵
相对熵(Kullback-Leibler divergence,KLD),也叫KL散度,用来量化两个概率分布的差别。计算式为
(11)
根据式(11)可知,如果两个分布p(xi)和q(xi)相同,那么相对熵等于0;若p(xi)和q(xi)略有差异,其值就会大于0,所以相对熵值越小则表明两个概率分布之间的差异越小[23],熵值越大则差异越大。故本文引入KLD作为噪声和信号分量的判定准则。
1.3.3 降噪流程
本文用IA对VMD参数进行全局优化,实现原始信号各分量的有效分离。
IA-VMD结合KLD降噪的具体流程如图1所示。以输入信号的样本熵作为IA的亲和度函数,搜索样本的最佳参数组合[K,α];按照优化后的[K,α]对信号进行VMD分解,得到K个IMF分量;计算各IMF分量的KLD值,并将KLD值作为噪声分量的判定标准;根据KLD值识别噪声分量并剔除,将剩余分量重构得到降噪后的信号;最后利用短时傅里叶变换进行特征提取。其中,IA优化VMD的参数设置包括:K的范围是[2,10],α的范围是[1,5000],迭代次数为50次,交叉速率是0.9,种群规模为10。

图1 IA-VMD降噪流程图
2 仿真分析
浮环密封等旋转机械的声发射信号,具有频域范围宽的特点,一般是由正弦、调频和调幅信号组成的仿真信号,难以模拟真实的声发射信号。本文采用Mitrakovic等[24]提出的连续声发射信号数学模型,表达式为
(12)
式中,Ai,αi,fi和ti分别为第i个信号的幅值、衰减系数、特征频率和峰值时刻。
声发射模拟信号参数如表1所示,采样频率500 kHz。

表1 声发射模拟信号参数
在仿真声发射信号中加入信噪比为10 dB的高斯白噪声,其纯净信号如图2所示。

图2 纯净信号
亲和度函数变化曲线如图3所示,在迭代20次后达到收敛,最佳参数组合为[5,3822]。设置优化后的参数,经过VMD分解得到5个IMF分量。

图3 亲和度函数变化图
IA-VMD分解得到的频谱,如图4所示,在有噪声干扰的情况下,70 kHz、80 kHz和160 kHz成分与原始信号特征频率吻合,且IMF2-IMF4的时域图波形与图2一致,分别在4 ms、12 ms和8 ms处出现波峰。同时计算各个分量的KLD值,结果如图5所示,IMF1和IMF5的KLD值,明显高于其他三个分量,说明这两个分量与原始信号差异最大,可以认为是噪声分量;同理IMF2-IMF4的KLD值较小,说明这三个分量与原始信号差异较小,将其重构得到降噪信号。
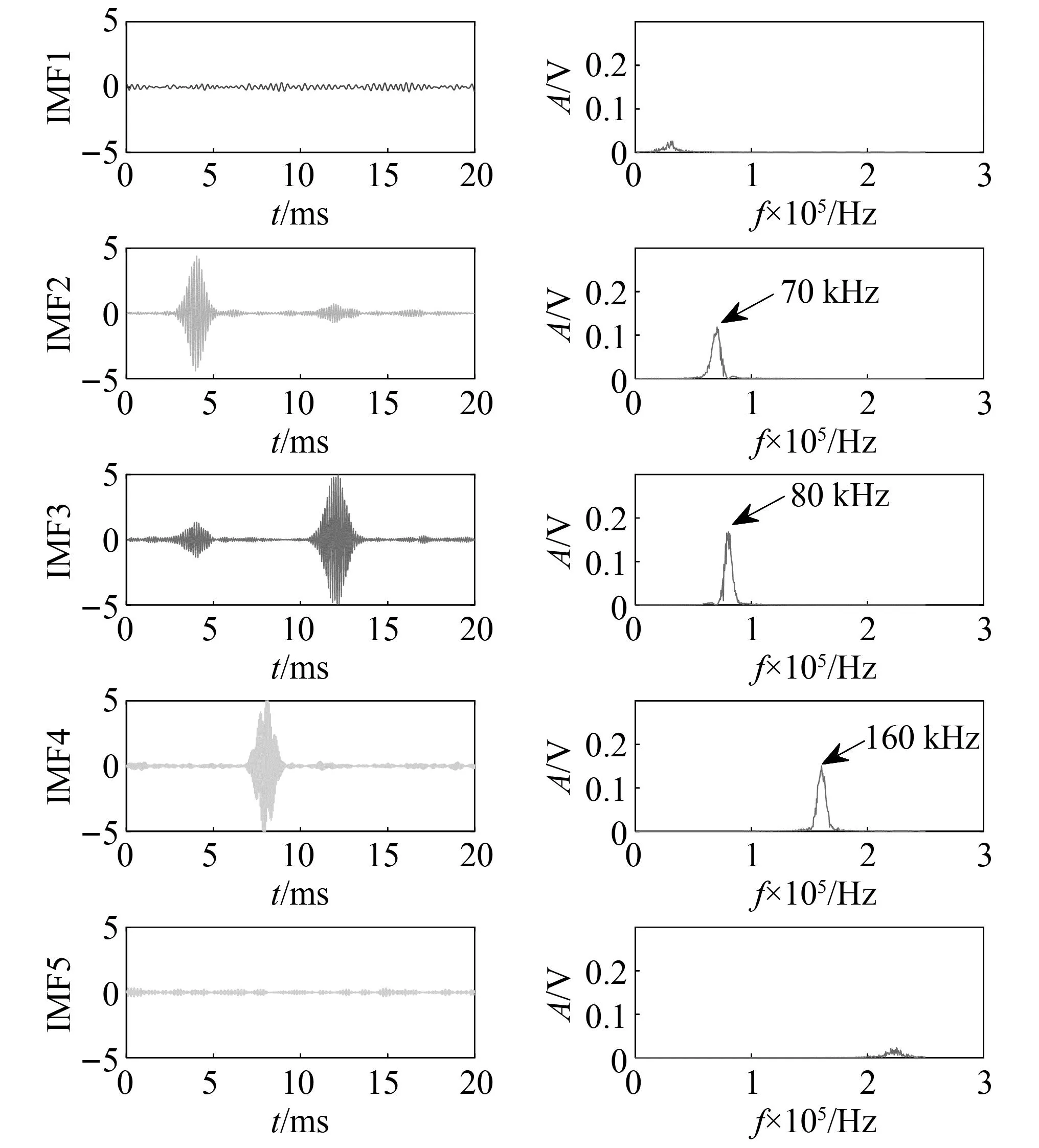
图4 IA-VMD处理结果
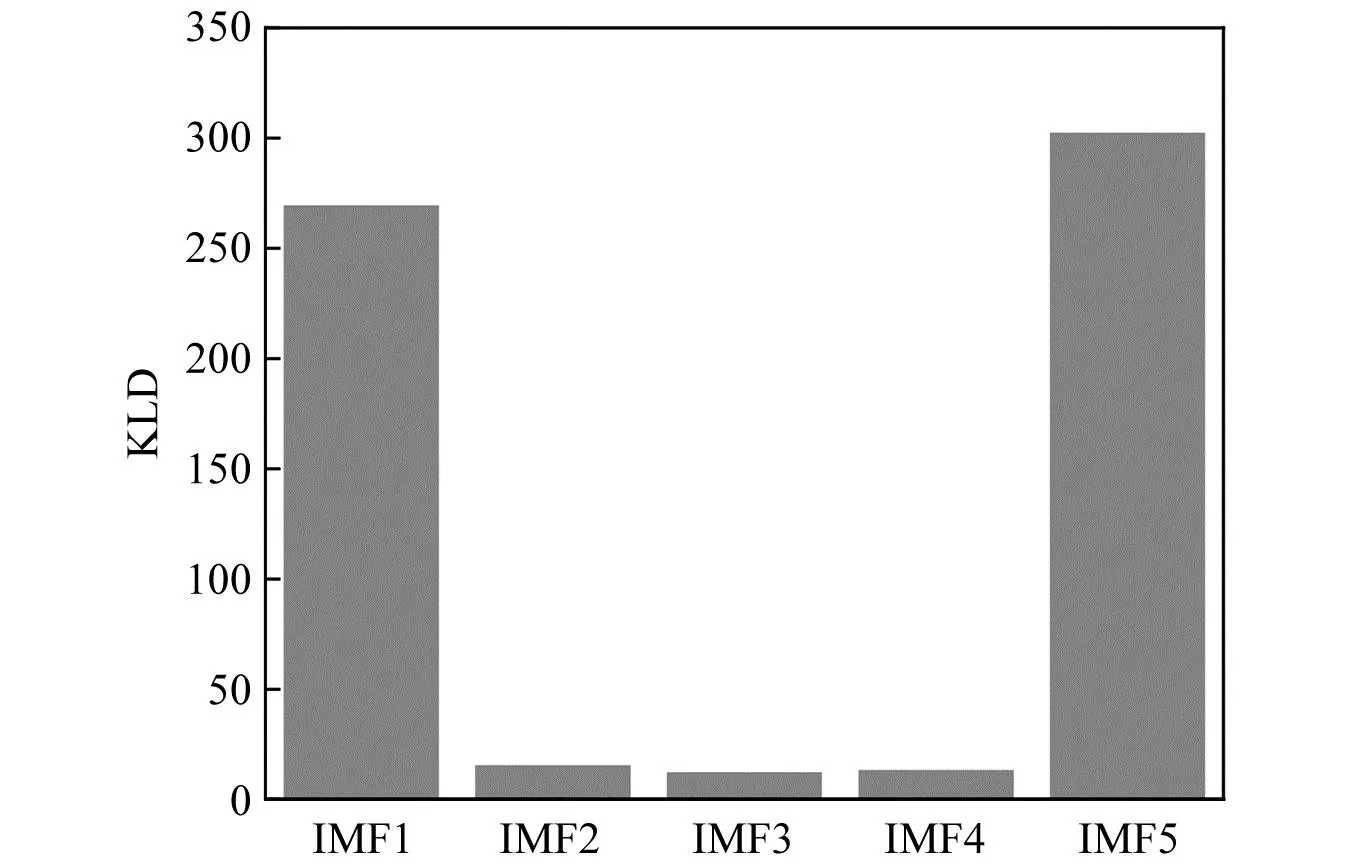
图5 各阶分量的KLD值
为了定量分析和说明IA-VMD算法的降噪效果,将信噪比SNR和相关系数R作为评价指标,即
(13)
(14)

如表2所示,人为选取4组VMD参数,与本文方法对比,信噪比分别降低了7.42 dB、7.94 dB、6.68 dB、4.29 dB,相关系数分别降低了0.07、0.08、0.05、0.02,说明未经过参数优化的4组数据,降噪效果明显不如经过算法优化后的。IA-VMD方法与粒子群优化(particle swarm optimization-variational mode decomposition,PSO-VMD)、鲸鱼优化(whale optimization algorithm-variational mode decomposition,WOA-VMD)以及遗传算法优化(genetic algorithm-variational mode decomposition,GA-VMD)方法相比,信噪比分别提高了3.92 dB、3.16 dB 、0.57 dB,分别增益34.42%、26.01%、3.86%;相关系数分别提高了0.03、0.02、0.01。结果表明,经过IA-VMD方法降噪精度更高,分解效果更优。

表2 降噪效果评价
3 工程应用
3.1 浮环密封工作原理
浮环密封主要由壳体、密封环、挡圈、波形弹簧、垫片等组成[25],其中密封环由金属环和浮环组装而成,如图6所示。

图6 浮环密封结构示意图
浮环密封的工作原理与滑动轴承类似,工作前浮环受重力与主轴外壁贴合,两者之间间隙极小。浮环密封运行后,浮环沿径向高频上下浮动时,波形弹簧使浮环端面与壳体相接触,浮环端面与壳体间产生干摩擦而形成次密封面,工作时干摩擦运动一直存在。浮环与主轴间形成的流体膜即为主密封面,防止高压侧气体泄漏。工作初期由于密封间隙动压不足会引起主密封面碰摩,浮环易产生冲击裂纹,导致泄漏量增大,因此本文重点研究浮环密封主密封面的碰摩声发射信号特征。
3.2 试验方案
浮环密封试验装置如图7、图8所示。密封环结构见图8,动环为双端面螺旋槽型,材质为碳化钨,浮环材质为石墨。浮环密封结构参数和动力学参数如下:槽深为8 μm,槽数为12,浮环宽度20 mm,动环外径50 mm,动环宽度50 mm,螺旋角 30°,槽长为10 mm。声发射信号采用PXR15声发射传感器采集,前置放大器增益40 dB,采集频率2 MHz。

图7 浮环密封装置实物图

图8 密封环结构
试验包括两种工况,工况1:槽深为8 μm运转试验,试验压力为0.2 MPa,匀速提升2 000 r/min后,保持转速持续10 s,并记录该过程中的声发射信号;工况2:(对照试验)将密封环拆下,重复工况1中的操作并记录该过程中的声发射信号。
3.3 信号处理
为获得浮环密封的声发射特征信息,对工况1采集的声发射信号进行降噪处理,对VMD参数进行优化得到最佳参数为[7,3 327],其分解结果如图9所示。

图9 IA-VMD处理结果
其中IMF2和IMF3的中心频率分别为170 kHz和100 kHz与下文工况1的时频分析结果相符合,可以反映浮环密封声发射特征信息。IMF5、IMF6、IMF7所对应的中心频率为66 kHz、78 kHz和85 kHz与下文工况2的时频分析结果一致,说明是与原始信号无关的噪声。
对噪声分量进行选择,如图10所示。根据相对熵原理可以看出IMF1-IMF4的KLD值都很小,说明与原始信号的差异小;IMF5-IMF7的KLD值较大,说明与原始信号差异较大,是与原始信号无关的固定噪声。

图10 各阶分量KLD值
对工况1降噪后的声发射信号做均方根散点图。如图11所示,将IMF5-IMF7剔除后,重构信号的均方根散点图规律与Towsyfyan等[26]的研究结果拟合曲线基本一致。AB段密封处于混合润滑状态,此时端面闭合;BC段密封处于流体润滑状态,此时端面开启;CD段密封运行平稳,达到平衡。验证了本文提出的降噪方法在浮环密封声发射信号提取的有效性。

图11 重构信号的均方根
为了保证声发射信号在降噪研究中的可靠性,进行了无密封环运行状态下对照试验(工况2)。结果如图12所示,可以看出声发射能量集中在15±5 kHz和80±10 kHz,与上文中的IMF5-IMF7中心频率一致,说明这些频率范围属于固定噪声,与设备主轴相关。

图12 工况2时频图
针对工况1不同阶段的浮环密封声发射信号,利用短时傅里叶变换,对试验结果进行时频分析。图13(a)是AB段运行过程的时频图,声发射能量主要集中在170±10 kHz、100±10 kHz处,此时密封面未开启,容易产生碰摩。图13(b)是BC段运行过程的时频图,声发射能量主要集中在100±10 kHz附近。图13(c)是BC段运行过程的时频图,声发射能量主要集中在100±10 kHz、15±5 kHz附近。当转速超过1 000 r/min后,所测信号几乎全部来自设备主轴[25],可以判断CD段声发射能量100±10 kHz和15±5 kHz频率段,主要来自设备主轴和次密封面干摩擦,这与工况2分析结果基本相符,而AB段的声发射能量170±10 kHz,主要是由主密封面碰摩形成。

图13 工况1时频图
4 结论
(1)建立了基于IA-VMD浮环密封声发射信号的降噪模型,通过免疫算法可以自适应地获取VMD的模态数量K和惩罚因子α。
(2)采用KLD直观地判断信号中的噪声分量,克服了用传统噪声阀值判断的不足。将KLD较大的IMF5-IMF7作为噪声信号滤除,KLD较小IMF1-IMF4作为有效信号保留。通过对比有效信号的均方根值的变化规律,验证了浮环密封声发射信号降噪的有效性。
(3)降噪后的声发射信号,通过短时傅里叶变换,得到浮环主密封面的碰摩特征频率为170±10 kHz,对浮环密封乃至非接触机械密封故障诊断具有重要意义。
