基于轮轨切向力的防空转/滑行效率计算方法研究

陈 玉,田敬雷,李洪智,丛 明

(中铁检验认证(青岛)车辆检验站有限公司,山东 青岛 266031)

随着“走出去”战略的实施,出口地铁车辆越来越多,在进行出口地铁项目防空转/滑行试验时,多采用防空转/滑行效率来评价地铁车辆防空转/滑行的性能。而防滑行试验的相关标准UIC 541-05:2005[1]与EN 15595:2018[2]中规定的防滑行试验评价方法主要适用于高速铁路车辆防滑行试验评价,不完全适用于地铁车辆防空转/滑行试验的评价,同时以上标准也没有规定防空转/滑行效率的计算方法,目前常用的防空转/滑行效率的计算方法也不统一。本文通过对轮轨黏着机理及特性分析、车辆黏着控制策略进行研究,并结合车辆受力分析,提出了一种基于轮轨切向力的防空转/滑行效率计算方法,该方法同时适用于防空转试验和防滑行试验效率计算,结合试验数据,采用不同的防空转/滑行效率计算方法进行计算,由于该方法排除了车辆运行阻力对计算结果的影响,在不同试验工况下的计算结果一致性较好。

1 黏着特性与黏着控制策略

车轮在滚动过程中,从刚体运动学角度分析,当车轮在钢轨上做纯滚动时,车轮与钢轨之间没有相对滑动。从弹性力学角度分析,由于车轮和钢轨相互挤压,两者之间不是点接触。同时,由于轮轨间切向力的存在,轮轨椭圆形接触面内存在滑动区和黏着区[3]。轮轨间的切向力越大,滑动区占整个椭圆形接触面的比例越大,黏着区占整个椭圆形接触面的比例越小,当轮轨间的切向力增大至一定程度时,车轮和钢轨之间就会出现相对滑动,车轮就会打滑[4]。

现在普遍采用黏着蠕滑理论来分析轮轨之间的切向作用力,为了区分黏着力与黏着系数等概念,本文将轮轨间可能达到的最大切向作用力称做黏着力,将轮轨间实际的切向力称做轮轨切向力。将黏着力与钢轨对车轮的法向反力的比值称做黏着系数,将轮轨切向力与钢轨对车轮的法向反力的比值称做切向力系数[5],将车辆牵引或制动系统施加的力称做牵引力或制动力。

由于蠕滑现象的存在,结合刚体平面运动学中速度瞬心的定义,牵引过程中动轮的圆周速度ωR大于列车行驶速度Vcar(Vcar=ω×OO′),制动过程中车轮的圆周速度ωR小于列车行驶速度Vcar,车轮圆周速度和列车行驶速度之间的矢量和ΔV(ΔV=ω×O′C)称为蠕滑速度,如图1所示。蠕滑速度与列车行驶速度的比值叫做滑移率或蠕滑率[6]。

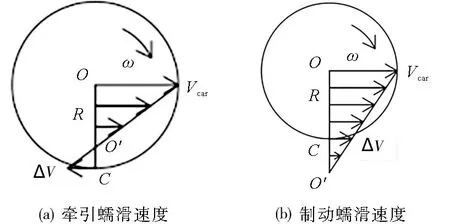
O—车轮圆心;O′—速度瞬心;ω—车轮转速;R—车轮半径;C—轮轨接触点。

黏着系数与蠕滑率的关系称为黏着特性,经研究表明:当轨面情况一定时,轮轨间的黏着系数随蠕滑率的增大而增大,这一区间称为稳定区。当黏着系数达到峰值后,蠕滑率继续增大,黏着系数会减小,这一区间称为非稳定区。在不同轨面条件下,相同的蠕滑率对应的黏着系数是不同的[6-7],如图2所示。

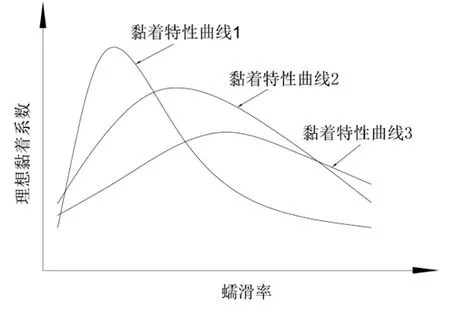
图2 不同轨面条件下的黏着特性曲线

由轮轨黏着特性可知,当黏着系数处于稳定区域时,牵引力或制动力增大,会导致蠕滑率增大,蠕滑率增大会导致黏着系数增大,进而轮轨切向力可进一步增大,轮轨切向力与牵引力或制动力仍可匹配,车辆可以稳定运行。当黏着系数处于非稳定区域时,牵引力或制动力增大,会导致蠕滑率增大,蠕滑率增大会导致黏着系数减小,进而使轮轨切向力减小,牵引力或制动力与轮轨切向力无法匹配,车轮就会出现空转或滑行现象。

由轮轨黏着特性曲线可知,想要充分利用黏着系数,只要使车辆的切向力系数工作于黏着系数的峰值点即可[8]。但在工程实际中,轮轨间的黏着状态不断变化,不同的黏着控制策略对黏着的利用不尽相同。目前存在的黏着控制方法主要有下文所述的几种。

1.1 传统黏着利用控制法

传统的黏着利用控制法是在空转和滑行发生后,通过减少车辆牵引力或制动力来实现黏着利用控制,该方法首先需要大幅度地降低车辆牵引力或制动力以消除空转或滑行,然后再缓慢地恢复车辆牵引力或制动力,以防止车辆空转或滑行情况进一步恶化。在这样的方法下,切向力系数常常远小于黏着系数峰值点,因此黏着利用率较低[8]。

1.2 直接蠕滑速度法

由黏着特性曲线可知,在列车行驶速度一定的情况下,稳定区蠕滑速度增加,黏着系数增加,轨面可以提供更大的轮轨切向力,可与之匹配的车辆牵引力或制动力也会增加。当蠕滑速度由稳定区移动到非稳定区时,轨面可以提供的轮轨切向力减少,车辆牵引力或制动力应随之减小。同理,蠕滑速度由非稳定区减小至稳定区时,黏着系数、车辆的牵引力或制动力也会增大至峰值,然后减小,直接蠕滑速度法就是利用上述原理实现黏着控制的。使用直接蠕滑速度法时,需准确获取轴速和车速,蠕滑速度是已知的,车辆通过检测蠕滑速度与车辆牵引力或制动力的变化情况,反复调节蠕滑速度,使车辆的切向力系数在黏着系数峰值处不断变化。直接蠕滑速度法无法使车辆始终维持在黏着系数峰值处工作,无法始终获得最大的牵引力或制动力。但可以优化算法使切向力系数偏离黏着系数的范围减小,从而提高平均牵引力或制动力。另外该方法可以循环调节蠕滑速度,实现了黏着系数峰值点的自动搜寻[8]。

1.3 间接蠕滑速度法

直接蠕滑速度法需要准确获取轴速和车速,这一方法一方面会增加车上的设备,另一方面在车辆起动或恶劣天气条件下测速精度较差,为避免上述问题,在直接蠕滑速度法的基础上又形成了间接蠕滑速度法。由直接蠕滑速度法可以发现,蠕滑速度的大小并不重要,重要的是如何确定蠕滑速度的调节方向以及如何调整蠕滑速度[8]。在此基础上,提出了间接蠕滑速度法。间接蠕滑速度法检测车辆加速度、转速、牵引力或制动力,并记录运行过程中上述物理量的极值,通过上述物理量实际值与给定值的比较,确定蠕滑速度的调节方向与增量。

1.4 相位移法

根据黏着特性曲线可以发现,黏着系数峰值左侧的稳定区域,曲线斜率大于0;黏着系数峰值右侧的非稳定区域,曲线斜率小于0;黏着系数峰值处,曲线斜率为0。如果能够实时地获取车辆在运行过程中的黏着特性曲线的斜率,并使车辆黏着的斜率始终处于0,就能实现黏着的最佳利用。工程实际中无法直接获得黏着系数斜率,有人提出了间接获得切向力系数斜率的相位移法[8],这一方法建立在线性系统理论的基础上,基本原理是通过对切向力系数工作点的局部线性化处理,得到局部线性化的车辆传动系统动力学模型,通过在系统输入信号即电机转矩上叠加一定频率和幅值的正弦信号,对系统输出信号即电机转速进行滤波处理,得到叠加的正弦信号激励的系统输出,利用正交相关法计算得到相位移。由于在某一频率时,相位移与切向力系数斜率存在单值对应关系,对切向力系数斜率的计算与控制就转变为对系统相位移的计算与控制,从而实现对车辆的黏着控制。

1.5 切向力系数导数法

列车行驶速度一定的情况下,由于黏着力与蠕滑速度呈现非线形关系,影响因素多,黏着曲线峰值点处黏着系数对蠕滑速度的导数难以确定,但可以通过切向力系数和蠕滑速度分别对时间求导的方法进行简化,由于车辆加速和减速过程中,蠕滑速度总是不断变化的,蠕滑速度对于时间的导数最多只在某几点处为0,要想求得切向力系数对蠕滑速度的导数为0,只需获得切向力系数对时间的导数为0,这样切向力系数斜率为0的搜寻就变成了切向力系数对时间的导数为0的搜寻。通过单个车轮运动模型可得轮轨切向力F的运动方程:

(1)

式中:T为电机转矩,Jn为折算到车轮的转动惯量,t为时间。

在计算出轮轨切向力的基础上,可以通过对切向力系数的导数的判断近似完成对黏着峰值点的判断和搜寻[8]。

1.6 其他控制方法

除上述方法外,还有模糊控制法、神经网络控制法、GPS检测法、电流控制法等黏着控制方法[9]。这些方法也都无法实现黏着特性的精确描述。

通过对上述黏着控制策略的研究可知,目前缺少定量的黏着特性描述方法,车辆黏着控制策略只能实现切向力系数对黏着系数的逐渐逼近,无法使车辆始终在黏着系数峰值工作,因此无法使用黏着力或黏着利用率作为防空转/滑行效率的评价方法,只能采用近似计算或使用其他物理量进行评判。

2 现有防空转/滑行效率计算方法

关于防空转/滑行效率的计算,通过查找相关文献[10-11]并结合地铁项目试验经验,共获得以下7种计算方法。

(1) 上海地铁1号线技术规格书中对防滑行效率做了定义,防滑行效率e为给定条件下(黏着系数0.05～0.08,速度8 km/h以上),起防滑作用的时间里的理想制动距离与实际制动距离的比值,即:

(2)

式中:S1为给定黏着下理想制动距离,S2为防滑系统工作后的实际制动距离。

本文试验验证时采用黏着系数0.08条件下,车辆从开始滑行减速至8 km/h或黏着情况改善时的理论制动距离作为理想制动距离。

(2) 减速度线性假设下的计算公式1,如下:

(3)

式中:a0为滑行出现时的减速度峰值,表示可能的最大黏着条件;v1为开始滑行时的瞬时速度;v2为黏着情况改善时的速度或8 km/h;T为v1、v2之间的时间差。

(3) 减速度线性假设下的计算公式2,如下:

(4)

式中:S为v1、v2之间车辆走过的实际制动距离。

(4) 平均减速度法。取整个滑行期间n个减速度主峰值的平均值作为理想制动距离的基础,形成以下公式:

(5)

式中:amax为减速度峰值。

(5) 最大黏着的包络线公式。通过等间隔选取减速度最大峰值来形成包络线,使用实际减速度包络线作为理想黏着条件,计算出这一黏着条件下的速度变化值,然后按实际试验的速度变化值v1-v2计算出折算因子Γ,用其压缩时间坐标计算理想制动距离。计算公式如下:

(6)

式中:t1、t2为速度v1、v2对应的时刻,a(t)为减速度包络。

文献[10]中未明确折算因子的计算方法,本文试验验证时无法采用上述方法计算。为此在上述计算方法基础上形成新的计算方法,如下:

(7)

式中:S包络为由减速度包络线作为理想黏着条件,车辆在这一黏着条件下计算出的理想停车距离。

(6) 克诺尔公司定义的防滑行效率,如下:

(8)

式中:S假定为由第一个轴速度开始下降时的初始速度v、初始减速度aT计算得出的理想停车距离,S测量为从第一个轴速度开始下降到车辆静止时测得的停车距离。

(7) 在国外地铁项目防空转/滑行试验中,有的项目采用以下方法计算防空转/滑行效率:

(9)

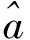
从制动距离的角度分析,方法(1)、(3)、(4)、(5)、(6)可以认为是使用理想制动距离与实际制动距离作比值求出防滑行效率。各方法的区别在于如何计算理想制动距离,方法(1)使用给定的黏着条件计算理想制动距离;方法(3)使用滑行期间初末速度的平方差除以2倍的刚出现滑行时的减速度峰值作为理想制动距离;方法(4)使用滑行期间初末速度的平方差除以2倍的滑行阶段的n个减速度峰值的平均值作为理想制动距离;方法(5)使用实际减速度的包络线为基础计算理想制动距离,方法(6)与方法(3)类似。

从减速度或黏着的角度分析,方法(2)、(3)、(4)、(6)、(7)可以认为是使用实际平均减速度与理想减速度作比值求出防滑行效率。方法(2)、(3)、(6)取刚开始滑行的减速度峰值作为理想减速度;方法(4)取滑行期间n个减速度峰值的平均值作为理想减速度;方法(7)取减速度的包络作为理想减速度。图3给出了方法(2)、(3)、(4)、(6)、(7)理想减速度取值对比结果。由于减速度可以表征黏着条件,上述计算方法也可以近似认为是切向力系数与黏着系数作比值求出防滑行效率。

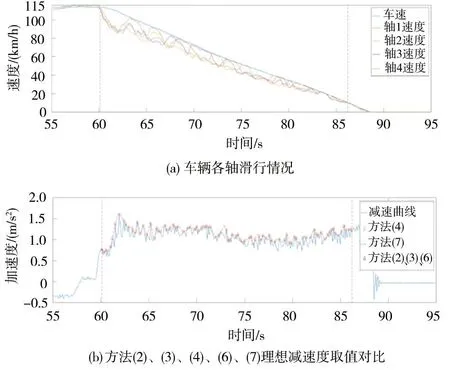
图3 方法(2)、(3)、(4)、(6)、(7)理想减速度取值对比

从方法(2)、(3)、(6)到方法(4)再到方法(7)可以看出,算法对于滑行期间黏着系数的估计越来越精确。但上述算法也存在一些问题:一是除了方法(7),其余方法均不适用于防空转试验效率评价;二是上述方法所采用的理想制动距离或理想减速度计算方法与理想黏着条件下的制动距离和减速度仍存在差距;三是减速度表征车辆受到的合力作用,使用上述公式计算未排除车辆运行阻力的影响。

根据车辆黏着控制策略分析,在空转/滑行过程中,车辆控制牵引力/制动力并改善黏着,使轮轨切向力逼近黏着力,利用轮轨切向力进行防空转/滑行效率计算,可以避免车辆运行阻力的影响,更好地估计空转/滑行过程中的理想黏着条件,更能表征防空转/滑行的性能。

3 基于轮轨切向力的防空转/滑行效率计算方法

由于车轮所受的横向力对车轮在行进方向上的运动状态无明显影响,故在以下分析过程中,忽略横向力的影响。车轮接触的外界物体包括:轨面、轴箱轴承、齿轮箱的啮合齿轮、闸瓦或制动盘。在牵引、制动状态下的车轮受力情况见图4。受力分析时,根据理论力学中的滚动摩擦理论将轨面对车轮的作用力向车轮与轨面的接触点简化为轨面对车轮的支持力Ft、轨面对车轮的滚动力偶矩MG、轨面对车轮的切向力Ff,将轴箱轴承对车轮车轴的作用力向车轮中心简化为垂直和水平方向上的正压力Fn、Fz,忽略简化过程中的附加力偶矩的影响。

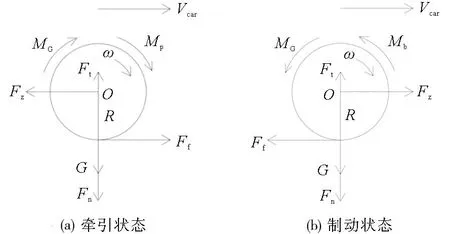
G—车轮自身所受的重力;Mp—齿轮箱啮合齿轮对车轮的牵引力矩;Mb—闸瓦、制动盘或齿轮箱啮合齿轮对车轮的制动力矩。

滚动力偶矩在方向上与牵引制动力矩一致,对车轮运动的作用一致,不再单独进行分析。

车辆处于牵引状态时,根据牛顿第二定律,并对车轮轴心取矩可得:

mwaw=Ff-Fz

(10)

Jα=Mp-Ff·R

(11)

式中:mw为车轮质量,aw为车轮加速度,J为车轮转动惯量,α为车轮角加速度。

车辆处于制动状态时,根据牛顿第二定律,并对车轮轴心取矩可得:

mwaw=Ff-Fz

(12)

Jα=Mb-Ff·R

(13)

当车轮未发生空转/滑行时,轨面对车轮的切向力Ff小于此时的黏着力,此时车轮角加速度与车轮加速度相匹配,即aw=α·R。随着牵引/制动力矩的增大,切向力Ff逐渐增大,直到等于黏着力。当牵引/制动力矩继续增大,轨面能提供的切向力无法继续增大,车轮角加速度与车轮加速度不匹配,即aw<α·R,此时车轮进入空转;当制动力矩继续增大,轨面能提供的切向力无法继续增大,车轮角加速度与车轮加速度不匹配,即aw>α·R,此时车轮进入滑行,轨面对车轮的切向力等于黏着力。车轮进入空转/滑行状态后,车辆通过控制牵引/制动力矩改善轮轨间黏着,改善轮轨切向力,实现车辆的防滑保护功能。

考虑阻力的影响,建立单节车牵引、制动状态下的受力模型,如图5所示。

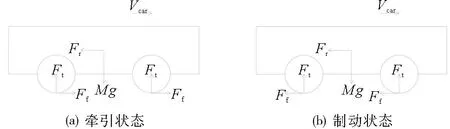
Fr—单节车的运行阻力;Mg—单节车的重力。

车辆处于牵引状态时,根据牛顿第二定律:

Md·ac=Ff-Fr

(14)

式中:Md为车辆等效质量,ac为车体加速度。

根据牛顿第二定律,由公式(14)可得:

Ff=Md·ac+Fr

(15)

车辆处于制动状态时,在水平方向上:

Md·ac=Ff+Fr

(16)

根据牛顿第二定律,由公式(16)可得:

Ff=Md·ac-Fr

(17)

根据以上分析可知,空转/滑行状态下单节车所受的轮轨切向力为:

Ff=Md·ac±Fr

(18)

其中,+用于空转过程,-用于滑行过程。

将列车运行阻力公式[12]代入公式(18)可得:

Ff=Mdac±mg(A+Bv+Cv2)

(19)

式中:m为车辆在整备状态下的质量,g为重力加速度;v为车辆速度,A、B、C为车辆运行阻力回归待定系数。

在空转/滑行过程中,根据车辆黏着控制策略和车轮受力分析,黏着力会在某些时刻与轮轨切向力相等,而大部分时间则是大于轮轨切向力,由于无法定量描述黏着力,本文采用轮轨切向力的包络近似替代黏着力,轮轨切向力的包络线由轮轨切向力曲线的局部极大值点通过样条曲线的方法拟合而成。在此基础上,防空转/滑行效率可以定义为轮轨切向力在滑行区间的积分与黏着力在滑行区间的积分的比值。

对于整个空转/滑行过程,基于轮轨切向力的防空转/滑行效率计算公式为:

(20)

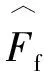
4 试验验证

本文利用现场车辆防空转/滑行试验验证基于轮轨切向力的防空转/滑行效率计算方法正确性。为了验证不同制动工况、不同速度等级下各计算方法计算防滑行效率的区别,本文进行了112 km/h、80 km/h和48 km/h速度等级下全常用制动防滑行试验、纯空气全常用制动防滑行试验和紧急制动防滑行试验,每种制动工况各速度等级下均取正反方向2份试验数据,共18份试验数据,其初始黏着系数均小于0.08;为验证各计算方法计算防空转效率的区别,本文进行了112 km/h速度等级下全牵引试验,共取5份试验。受试验线路长度限制,无法进行运行阻力的试验,方法中使用的运行阻力为车辆设计文件中的理论数据。

由于计算方法(1)～(6)针对车辆防滑行试验提出,不完全适用于车辆防空转效率计算,如方法(1)需要车辆减速到8 km/h,在防空转试验中不可能出现,为了在试验验证阶段使用该方法进行计算,需要将该计算方法的计算区间改为车辆开始空转到空转结束的速度区间,其余计算方法相同。方法(5)、(6)的计算需要减速至车辆停止,不适用于防空转试验,不再将该方法用于防空转效率评价。本文采用Matlab软件进行数据处理,相关试验结果见图6、图7。

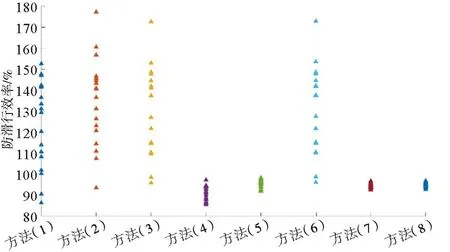
图6 防滑行效率试验结果分布图

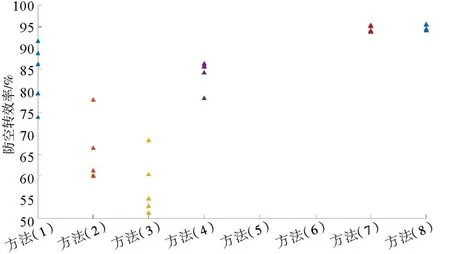
图7 防空转效率试验结果分布图

方法(1)大部分防滑行效率试验结果大于100%,说明整个滑行过程中的平均的黏着系数要大于0.08。防空转效率试验结果小于100%,说明整个空转过程中的平均的黏着系数要小于0.08。防滑行效率试验结果大于100%的原因是由于在车轮滑行过程中,防滑装置的动作改善了轮轨黏着条件。防空转效率试验结果小于100%的原因是随着车辆速度的增加,车辆的剩余加速度减小,车辆能提供的牵引力大幅减小,尽管牵引系统的动作能一定程度地改善黏着条件,却无法在该计算方法中起决定性作用。由此可知,方法(1)在防滑行试验中的计算结果存在不合理的情况,在防空转试验中存在容易受到车辆牵引特性影响导致防空转效率计算结果偏小的问题。

方法(2)、方法(3)与方法(1)存在同样的问题。

方法(4)防空转/滑行效率试验结果均小于100%,该算法避免了方法(1)、(2)、(3)中出现的问题,但由于只选取加减速度的峰值进行计算,存在过低估计防空转/滑行效率的可能。

方法(5)改善了方法(4)中过低估计防空转/滑行效率的问题,但由于原方法的折算因子计算方法未知,改进后的新方法暂时只适用于防滑行效率计算。

方法(6)与方法(3)类似,无法避免防滑行效率试验结果大于100%的不合理问题,同时也不适用于防空转试验。

方法(7)的试验结果相较于方法(4),防空转/滑行效率有较为明显的提高,改善了方法(4)过低估计防空转/滑行效率情况。方法(7)的部分试验结果小于方法(4)的试验结果是由于两者用于计算的滑行区间不同,方法(4)的计算滑行区间速度最低可至8 km/h,方法(7)的计算滑行区间最低可至1 km/h左右。

方法(8)即本文提出的基于轮轨切向力的计算方法,从试验结果可以看出,相较于方法(7),防空转/滑行效率计算结果有一定的提高。由于方法(8)与方法(7)的空转/滑行计算区间是一致的,该部分试验结果的提高是因为计算方法考虑了车辆运行阻力的影响。相较于其他方法,方法(8)未出现防空转/滑行效率大于100%的问题,可以分别适用于防空转和防滑行试验,同时试验结果方差小,具有良好的一致性。

5 结束语

本文通过分析轮轨黏着特性、车辆黏着利用控制原理,并结合车辆的受力分析,提出了一种基于轮轨切向力的防空转/滑行效率计算方法,该方法适用于防空转试验和防滑行试验效率计算,与现有防空转/滑行效率计算方法相比,该计算方法排除了车辆运行阻力对计算结果的影响,得到的结果避免了防空转/滑行效率大于100%的情况,在不同工况下的试验结果具有良好的一致性。