板式轨道线路对机车垂向振动影响

蒋 超,李传龙,姚 远

(1.西南交通大学 轨道交通运载系统全国重点实验室, 四川 成都 610031;2.大连机车车辆有限公司 转向架开发部, 辽宁 大连 116022)

随着我国轨道交通的快速发展,轨道交通已成为主要公共交通工具之一,但随之也出现了许多如车体异常振动等影响车辆运行舒适性、平稳性的问题。车辆在轨道不平顺作用下,随着线路劣化及运行速度提高,车体结构振动也随之加剧,当达到特定条件时,车体结构共振将导致车辆运行平稳性变差并造成车体结构疲劳破坏。

常规车辆动力学分析将车体简化为刚性体,随着轨道车辆的高速及轻量化,为了准确模拟车辆动力学性能,需要建立考虑车体弹性振动的刚柔耦合动力学模型,将车体考虑为柔性体进行铁道车辆运行性能的研究。在已有的相关研究中,CARLBOM[1]通过有限元软件建立了柔性车体,研究了车辆的乘坐舒适性能等。曾京等[2]建立了铁道客车垂向振动系统数学模型,进行了客车系统幅频特性分析和随机响应分析。曹辉等[3-4]建立了考虑车体弹性的高速列车垂向刚柔耦合动力学模型,在频域内研究弹性效应下的振动特性及其传递关系,以及车辆系统悬挂参数和运行参数对振动的影响。赵义伟等[5]对比了柔性车体与刚性车体的车辆系统相关动力学性能。肖乾等[6]建立了含柔性车体的地铁头车模型,研究了柔性车体地铁车辆动力学特性。郭林生等[7]建立了含有车下设备的柔性车体刚柔耦合模型,分析了城轨车辆柔性车体中部与转向架上方的振动响应。罗志翔等[8]以地铁车辆为研究对象,建立了考虑车体柔性的刚柔耦合系统动力学模型,以转向架悬挂参数和设备悬挂参数为优化对象,对车辆垂向振动进行了优化研究。柔性车体动力学相关研究众多,但涉及柔性车体在不同轨道运行时的研究还不够充分。

本文针对国内实际运营动力集中动车组的机车在板式轨道线路运行时垂向振动剧烈的现象开展了研究,利用UM软件建立了考虑车体弹性振动的机车刚柔耦合多体动力学仿真模型,针对车体垂向振动及引起振动相关因素进行了分析,同时建立了考虑钢轨弹性及轨道板弹性的板式轨道模型,研究分析了机车通过板式轨道时的垂向耦合振动特性。

1 刚柔耦合动力学模型

1.1 柔性体动力学理论

相关柔性体的运动可以采用浮动参考坐标系进行描述,在总体惯性坐标系中,柔性体参考坐标系上的任意一点k的位置矢量定义为:

(1)

采用模态叠加法表示柔性体微小弹性位移:

(2)

式中:H为模态矩阵;hj为第j阶模态值;wj为第j阶模态对应的模态坐标。

柔性体应变、应力可分别表示为:

ε=Dxk

(3)

σk=Hε=HDxk

(4)

式中:D为弹性矩阵。

将式(1)～式(4)代入基于虚功原理的柔性体运动方程中,得到柔性体在多体系统中的运动方程:

(5)

传统的刚体动力学模型将物体均考虑为刚性体,而刚柔耦合动力学模型将某些部件考虑为柔性体,计算时将物体的微小变形也考虑在内,计算结果相较于传统刚体模型更为精确。

1.2 有限元模型建立

本文以某型动力集中动车组动力机车为研究对象,首先利用有限元软件ANSYS建立车体有限元模型,如图1所示,车体单元数为44×104,节点数为41×104。

图1 车体模型

利用ANSYS软件对车体有限元模型进行模态计算,前6阶模态为车体刚性模态。车体一阶垂弯频率为10.5 Hz。

同时利用有限元软件ANSYS建立了简化轨道板有限元模型,轨道板尺寸如表1所示。

表1 轨道板尺寸参数

1.3 车辆-板式轨道刚柔耦合模型

将车体有限元模型和轨道板有限元模型导入动力学软件UM,基于车辆-轨道耦合动力学理论[9],建立机车刚柔耦合模型,车辆主要结构参数如表2所示。

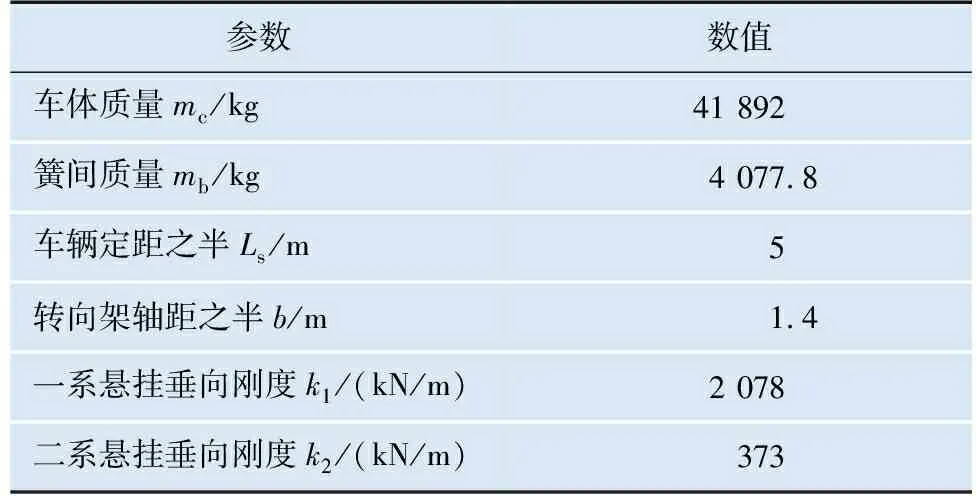
表2 车辆主要结构参数

软件提供无质量钢轨模型、移动质量钢轨模型以及柔性轨道模型,按需要选择轨道为柔性轨道,其钢轨采用铁木辛柯梁模拟,轨枕为左右两个半枕刚体模型,分别具有横向、垂向及侧滚自由度。该柔性轨道支持Kik-Piotrowski多点接触算法。

板式轨道的建立过程是将轨道板有限元模型导入动力学软件中作为轨下基础并与钢轨连接。扣件采用弹簧阻尼单元模拟,隔振垫、CA砂浆层和土层连接采用离散的弹簧阻尼单元模拟。在UM软件中建立的车辆-板式轨道刚柔耦合动力学模型如图2所示。

图2 车辆-板式轨道刚柔耦合动力学模型

2 车体振动响应分析

2.1 车体弹性振动特性分析

车辆运行速度对车体振动有着重要影响。车辆运行时受到轨道不平顺激励,轨道不平顺含有众多波长成分。当车辆以某一速度运行,车体的弹性固有振动频率与轨道激扰频率相等时,就会引起车体结构共振,该速度即为共振速度。车辆共振速度与车辆定距、轴距、车体频率等有关[3]。车体低频弹性振动以一阶垂弯频率为主,车体一阶垂弯模态出现共振的条件为车辆定距2Ls为轨道激励波长λ的整数倍,轨道激扰频率等于车体一阶垂弯频率f1,即:

(6)

根据公式,可得车辆一阶垂弯共振速度为:

(7)

根据公式,本文机车车体一阶垂弯频率f1为10.5 Hz,n取不同值时,机车一阶共振速度见表3。当共振速度处于机车正常运行速度附近时,将会引发车体结构共振,解决办法主要为减小相应轨道波长强度或者运行速度避开共振速度。

表3 车体一阶垂弯共振速度

机车在一阶共振速度及其附近速度运行时柔性车体垂向加速度频谱如图3所示。由图3可知,机车速度为126 km/h,即车体一阶垂弯共振速度时,机车司机室位置的垂向弹性振动明显大于速度为110 km/h及140 km/h时;表4为相应速度下机车垂向平稳性指标,车速为共振速度126 km/h时,车体垂向振动剧烈,该速度下垂向平稳性指标较110 km/h及140 km/h更大,故车辆运行速度应尽量避开一阶垂弯共振速度。

表4 不同速度下平稳性指标

图3 车体垂向加速度频谱

随着运行里程增加,车轮一阶不圆是实际运营时常见故障之一,应着重关注。当机车受车轮一阶不圆激励时,对应一定运行速度,激振频率与车体固有振动频率相等,同样会引发车体结构共振,从而影响运行平稳性及结构疲劳可靠性。

车轮一阶不圆对应激励频率与车速有关,一阶不圆激励频率为:

(8)

公式中d为车轮直径,当激励频率fd与车体一阶垂弯频率f1相等时,引发车体一阶垂弯共振,则可得到共振速度为:

v=πdf1

(9)

该机车车体一阶垂弯频率f1为10.5 Hz,车轮一阶不圆激励对应共振速度为148 km/h,考虑车轮磨耗到限时对应共振速度为136 km/h。

假设车轮一阶不圆峰谷值为0.3 mm时,柔性车体司机室位置垂向加速度频谱如图4,各运行速度下的峰值频率与公式计算出的频率相当;在车轮一阶不圆激励作用下,机车运行速度为共振速度148 km/h时,车体弹性振动明显大于其余运行速度时;同时140 km/h时柔性车体垂向加速度频谱幅值大于160 km/h速度时,因为140 km/h速度时车轮一阶不圆激励频率更接近车体一阶垂弯频率,车体弹性振动更明显;运行速度120 km/h时车轮一阶不圆激励频率较小,与车体一阶垂弯频率相差较远,车体弹性振动不明显。

图4 车轮一阶不圆激励下车体垂向加速度频谱

2.2 车辆-轨道-轨道板耦合振动特性分析

针对动力集中动车组动力机车在板式轨道线路运行时垂向振动响应剧烈的现象,建立考虑钢轨弹性及轨道板弹性的板式轨道模型,考虑板式轨道耦合振动对机车垂向振动的影响,并且建立含有刚性车体、柔性车体等多种组合模型进行对比分析。

考虑轨道板长度L为4.96 m,轨道模型中包含20块相同轨道板,则板式轨道通过频率为:

(10)

考虑分析100～160 km/h速度范围板式轨道通过特性,相应速度下板式轨道通过频率见表5。

表5 板式轨道通过频率

2.2.1 轨道不平顺激励工况

机车柔性车体及刚性车体模型通过板式轨道及非板式轨道时对应的司机室垂向加速度如表6所示,柔性车体模型通过板式轨道时车体垂向加速度大于通过非板式轨道,刚性车体模型通过两种轨道时车体垂向加速度则无较大的变化。柔性车体因考虑到结构弹性振动,其计算结果与刚性车体模型计算结果有差异。

表6 不同车体模型对应司机室垂向加速度 m/s2

对于柔性车体的加速度响应,相对于非板式轨道线路,机车以160 km/h速度在板式轨道线路运行时,其加速度变化最大,车体垂向振动加速度增加8%。

为探究机车在轨道不平顺激励作用下车体垂向响应频率分布,图5为通过非板式轨道线路时两种车体垂向加速度频谱,刚性车体频谱无明显峰值;柔性车体在100 km/h、120 km/h、140 km/h速度下存在与车体一阶垂弯频率相近的振动峰值,160 km/h速度下无较明显峰值。

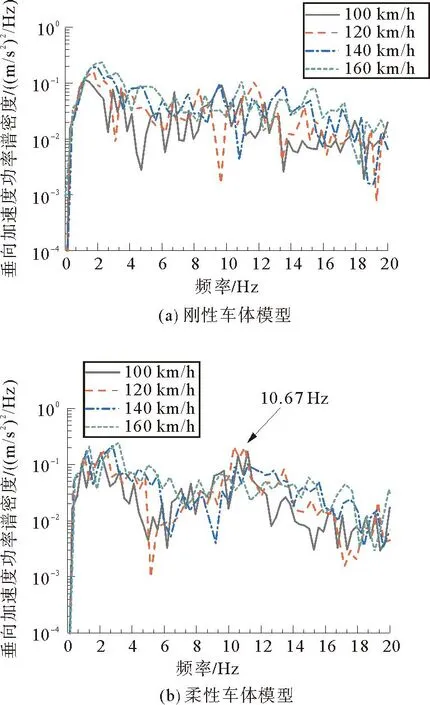
图5 轨道不平顺激励下非板式轨道车体垂向振动加速度频谱

通过板式轨道时车体垂向加速度频谱如图6所示。图6中刚性车体模型车体加速度频谱无明显峰值,与图5相比刚性车体在两种轨道下车体垂向响应无明显变化,即板式轨道对应通过频率对刚性车体垂向加速度响应无明显影响。图6柔性车体频谱在100 km/h、120 km/h、140 km/h速度下同样存在与车体一阶垂弯频率相近的振动峰值,但在120 km/h、140 km/h、160 km/h运行速度下,板式轨道对应通过频率的二倍频振动较为明显,故因为板式轨道通过频率二倍频振动,柔性车体通过板式轨道时车体垂向加速度大于通过非板式轨道。

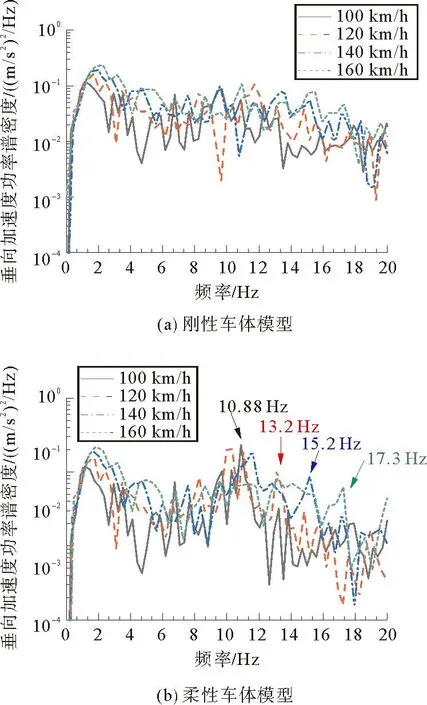
图6 轨道不平顺激励下板式轨道车体垂向振动加速度频谱

2.2.2 车轮一阶不圆激励工况

为探究车轮一阶不圆激励在机车通过板式及非板式轨道线路时对车体垂向振动的影响,考虑机车受到0.3 mm峰谷值车轮一阶不圆激励,由公式(8)计算得到各速度激励频率见表7。

表7 车轮一阶不圆激励频率

车轮一阶不圆激励下,机车柔性及刚性车体模型通过板式轨道及非板式轨道时的车体垂向加速度如表8所示。通过板式轨道时柔性车体垂向加速度明显大于通过非板式轨道,四个速度下其加速度增幅均较大,160 km/h时车体垂向振动加速度增加25%。刚性车体通过板式轨道时车体垂向加速度同样大于通过非板式轨道,但相对于柔性车体结果而言,其增幅较小。

表8 车轮一阶不圆激励车体垂向加速度

为探究机车在车轮一阶不圆激励下车体垂向响应频率分布,图7为通过非板式轨道线路刚性车体及柔性车体的垂向加速度频谱。

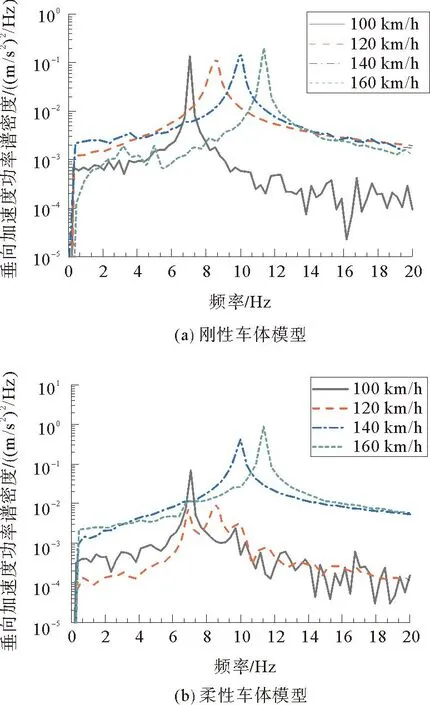
图7 车轮一阶不圆激励下非板式轨道车体垂向振动加速度频谱

图7中刚性车体频谱各速度峰值频率与车轮一阶不圆激励频率相同,且各速度峰值频率处幅值相当;柔性车体频谱同样存在相同频率峰值,但140 km/h、160 km/h速度工况因激励频率与车体一阶垂弯频率相近,频谱幅值较大,振动更为剧烈,故车体垂向加速度较大,100 km/h速度工况激励频率因与柔性车体局部模态相近,车体垂向加速度较120 km/h更大。

车轮一阶不圆激励工况机车通过板式轨道,刚性及柔性车体的垂向加速度频谱如图8所示。

图8 车轮一阶不圆激励下板式轨道车体垂向振动加速度频谱

图8刚性车体垂向加速度频谱中,除车轮一阶不圆激励频率峰值外,还存在小幅值板式轨道通过频率以及二倍频,故刚性车体通过板式轨道时车体垂向加速度大于通过非板式轨道。图8柔性车体垂向加速度频谱中,柔性车体除在车轮一阶不圆激励频率处振动明显外,板式轨道通过频率及其二倍频振动同样较为明显,且车体一阶垂弯频率处的振动幅值增大,故柔性车体模型通过板式轨道时其车体垂向加速度明显大于通过非板式轨道时车体垂向加速度。

3 结论

(1) 通过对比机车刚性及柔性车体模型通过板式及非板式轨道对应车体垂向振动响应,在轨道不平顺激励作用下,刚性车体在两种轨道运行时垂向响应无明显变化,柔性车体通过板式轨道时垂向加速度大于通过非板式轨道;柔性车体在两种轨道分别以100 km/h、120 km/h、140 km/h速度运行时,其垂向加速度频谱均存在与车体一阶垂弯频率相近的振动峰值频率,以120 km/h、140 km/h、160 km/h速度通过板式轨道时,对应板式轨道通过频率及二倍频率振动较为明显,运行速度为160 km/h时,相同轨道不平顺作用,机车在板式轨道线路运行时车体垂向振动加速度较非板式轨道增加8%。

(2) 考虑车轮一阶不圆的影响,机车通过板式轨道时,车体垂向加速度明显大于通过非板式轨道。相对于非板式轨道,通过板式轨道线路时,车体垂向加速度除车轮一阶不圆激励频率振动明显外,板式轨道通过频率及其二倍频振动同样较明显,且柔性车体一阶垂弯频率处振动幅值增大;运行速度为160 km/h,受峰谷值为0.3 mm车轮一阶不圆激励时,机车在板式轨道线路运行时车体垂向振动加速度较非板式轨道增加了25%。