结构优化在轨道车辆密封板设计中的应用研究
2024-03-01苑红磊王俊杰邹洪伟赵子豪李春超
苑红磊,王俊杰,邹洪伟,赵子豪,李春超,许 娇
(中车青岛四方机车车辆股份有限公司 国家高速动车组总成工程技术研究中心,山东 青岛 266111)
在工程应用领域,有限元不仅计算精度高,而且对于复杂形状的几何和载荷条件都能进行模拟,因此,有限元方法逐渐成为工程分析和产品结构设计的一个重要手段[1]。
对于轨道车辆行业来说,拓扑优化[2-6]的应用前景是十分广阔的,主要表现在以下几个方面:首先,车辆结构的传统设计中,车体结构的设计方案在很大程度上取决于设计师的经验。之后,需要由仿真工程师对设计师提供的模型进行强度计算和刚度校核,直到满足设计要求。对于复杂的结构来说,在有限元分析过程中,模型较难处理,并且计算量比较大。同时,很难对结构进行较大的改动,可供选择的方案比较少。此外,设计参数与结构的整体性能之间存在复杂的隐式关系,依赖于经验计算很难得到理想的设计。带来的后果就是在大多数的情况下,只能进行被动地设计[7-9]。
密封板作为高速动车组的重要零部件之一,在列车高速运行过程中,会受到气动载荷的影响。因此,在保证部件设计质量不变的前提下,提高密封板密封性能是十分必要的。本次研究在对列车线路运行数据进行采集后,利用有限元方法对当前结构进行分析,并通过拓扑优化数值计算方法为当前结构提供新的优化设计方案,不仅提高了设计的效率,也在很大程度降低了研发成本。本文主要是通过拓扑优化方法,为某车型的密封板提供最优的设计思路,并通过设计经验确定密封板结构的构型。结合尺寸优化方法[10]在保证密封板的总质量不变的前提下,提高密封板的刚度,从而进一步提高密封板的固有频率。避免列车在高速运行过程中,气动载荷的频率与密封板固有频率产生重合,导致共振现象的产生,提高列车运行的安全性及产品寿命。
1 结构优化常用算法
结构优化问题大多是隐式的目标或者约束。并且结构优化的不等式约束多于设计变量,因此,选择合适的最优化算法也是至关重要的。
结构优化过程中,优化准则就是把待优化的问题根据一定的假设,将其转化为数学问题。随后,根据建立的优化设计的准则和公式进行迭代求解。这种方法的优点是收敛速度较快,并且迭代次数比较少,在结构的优化过程中,对于大型结构在进行分析时使用准则法较多。优化准则法多用在约束条件不多的单约束优化问题中。
在使用优化准则法进行拓扑优化的求解过程中:(1)首先,需要定义初始设计区域,材料用量,边界条件;实际优化过程中,划分到设计域内的单元密度在优化过程中是随着迭代过程进行变化的;(2)确定结构所采用的单元类型,对结构进行有限元网格划分,初始化单元的设计变量,并根据单元刚度矩阵组装得到整体的刚度矩阵;网格划分由工程师完成,刚度矩阵的计算在软件中完成;(3)初始化单元的相对密度;(4)计算优化问题的目标函数及敏度值,求解拉格朗日算子;(5)通过优化准则去更新设计区域的变量值;(6)判断模型是否收敛,根据给定的收敛条件判定,如果不符合则需要重新迭代计算,若符合则可以输出优化结果图形及感兴趣的数据[8,11]。
2 初始结构计算分析
2.1 初始结构模型
本次研究的对象为某型号动车组密封板,其初始结构如图1所示。

图1 密封板初始结构
材料参数见表1。

表1 材料参数
2.2 试验数据采集
本次试验研究是在某型号列车正常运行状态下采用压力传感器采集密封板的内外空气压力。在两块密封板上共布置10个测点,测点布置如图2所示。
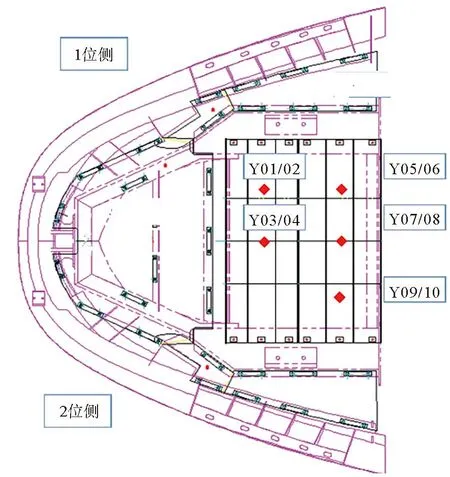
图2 测点布置示意图
在本次分析中,仅对布置有Y01、Y02、Y03、Y04测点的密封板进行分析,测点布置如图3所示,其中Y02和Y04布置在密封板的背面。

图3 测点布置现场图
根据列车实际运营情况,对空气压力数据信息进行采集。图4~图6为Y01点和Y02点、Y03点和Y04点的压差数据。
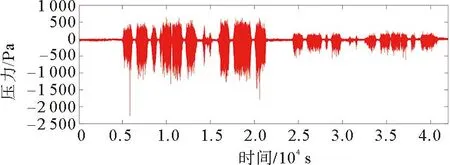
图4 Y01点和Y02点压差时域图
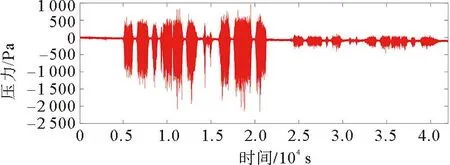
图5 Y03点和Y04点压差时域图

图6 Y01点和Y02点压差频谱
根据图6和图7中Y01点和Y02点、Y03点和Y04点的压差频谱分布曲线可知,在29 Hz附近,压差频谱曲线出现了明显的峰值。根据数据分析,在29 Hz处是容易引发结构共振的。因此,在实际运行过程中,密封板的固有频率需要避开峰值位置。

图7 Y03点和Y04点压差频谱
2.3 有限元模型及边界条件
对几何模型进行网格剖分,共划分17 056个单元,17 339个节点。有限元模型如图8所示。
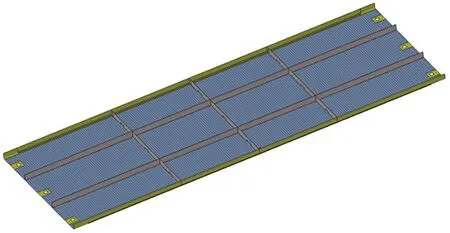
图8 初始结构有限元模型
其中,载荷施加方式及大小按照列车高速运行过程中现场试验采集数据施加,试验数据由压力传感器测得。将气动载荷简化为线性载荷,并且,载荷大小由中间位置1 500 Pa向1、2位侧线性递减为1 000 Pa。载荷分布示意图如图9所示。

图9 载荷分布示意图
其中,密封板是通过螺栓固定在列车底部的梁上。为了提高计算效率,对约束方式进行了必要的简化。简化后的约束方式为:在1、2位侧螺栓孔的位置进行约束。其中,1位侧约束X、Z方向位移及绕Y、Z轴转动;2位侧约束X、Y、Z方向位移及绕Y、Z轴转动。
3 最优传力路径分析及优化方案
3.1 模型简化
首先确定初始的拓扑方案。根据密封板的结构在HyperMesh中建立密封板的有限元模型作为拓扑优化的基结构。利用HyperWorks中拓扑优化求解模块对模型进行拓扑优化分析。其建模过程包括两方面内容:网格划分和添加材料属性。本次研究过程中,考虑到结构对称性特征,在划分网格时保证了网格的对称性。除此之外,为了提高仿真精度,采用了六面体网格。
对本次研究所采用的密封板的基结构进行了简化,如图10所示。
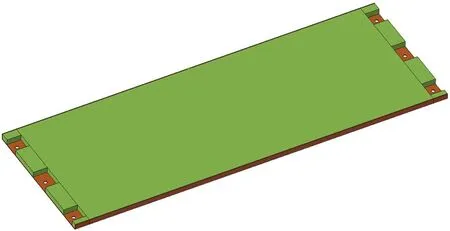
图10 基结构
其中,绿色区域为可设计域,灰色区域为不可设计域。
3.2 最优传力路径分析
先对简化的密封板模型进行网格划分,共划分了24 722个单元,29 708个节点。并赋予材料参数及施加边界条件后进行拓扑优化分析,边界条件与优化前结构保持一致。拓扑优化分析结果如图11所示。
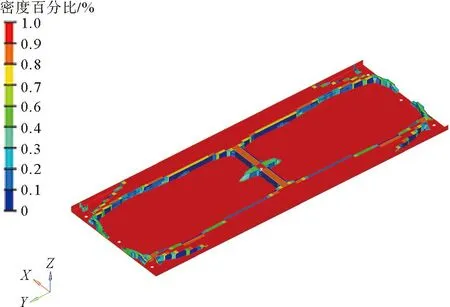
图11 拓扑优化分析结果
以上结果为当前载荷和约束下的最优传力路径。在结果分析中,因密封板宽度方向为车长方向,所以密封板中间位置的筋板称为纵向筋板;密封板长度方向为车宽方向,所以密封板两侧筋板称为横向筋板。根据实际设计经验,拓扑优化后的结果中的两根横向筋板延伸到了1、2位侧的螺栓孔的位置,并且与密封板的边界重合。为了避开螺栓孔带来附加的加工问题,因此考虑将横向筋板向内移动至螺栓孔中间位置。为了保证移动后的侧边的强度,沿长度方向在密封板的侧边设计了翻边。同时,考虑到工艺上的加工限制,根据工艺加工经验确定筋板的横截面形状及厚度。
将优化后的密封板几何模型进行网格划分,共划分了10 556个单元,11 127个节点。有限元网格划分结果如图12所示。
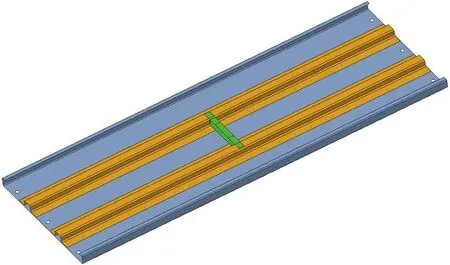
图12 密封板拓扑优化结构
其中,初步的设计方案中,根据设计经验给定密封板厚度为1.5 mm,优化结果中,筋板与密封板、纵向筋板和横向筋板的连接都采用点焊连接,焊点间距为50 mm。
对当前给定的板厚进行强度校核,计算结果如图13、图14所示。
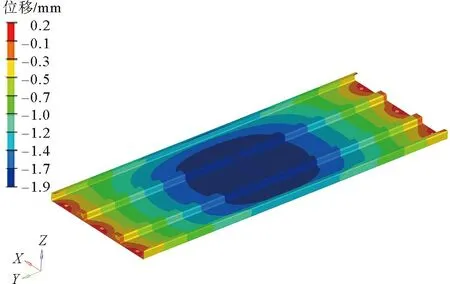
图13 拓扑优化结构垂向位移

图14 拓扑优化结构应力
根据计算结果和表2中对比可知,对拓扑构型进行初步优化后,最大应力发生在螺栓孔位置,大小为133.9 MPa,满足强度要求;刚度提高了70%;同时,筋板质量增加了2.45 kg,密封板底板质量减少了1.48 kg,总质量增加了0.97 kg。然而,采用拓扑优化的初衷是:在不增加结构质量的前提下,提高结构的刚度。因此,接下来需要继续对模型进行优化,使其进一步满足设计要求。
3.3 密封板结构尺寸优化设计
在拓扑优化的基础上对密封板结构优化后再进行尺寸优化,尺寸优化属于结构优化设计中的详细设计阶段。载荷和约束条件施加与拓扑优化相同,以底板厚度和筋板厚度为设计变量,降低部分刚度的前提下减小结构总质量,使结构质量满足设计要求。尺寸优化结果如图15所示。

图15 尺寸优化后的密封板和筋板厚度图
图15为尺寸优化后的密封板和筋板厚度示意图,优化后的底板厚度为1.4 mm,筋板厚度为1.2 mm。总质量由拓扑优化结构10.5 kg减少到9.35 kg,减少了10.9%,结构质量满足设计要求。接下来对密封板结构的刚度和强度进行校核。
3.4 尺寸优化前后方案对比
为了进一步对比尺寸优化前后列车密封板刚度变化情况,需要对新设计的方案进行有限元分析,载荷施加方式及大小如图9所示,约束方式与初始结构保持一致。尺寸优化后与初始结构的位移计算结果对比如图16所示。

图16 初始结构与尺寸优化后结构位移对比
根据位移计算结果可以得出优化前后的刚度结果,详细的对比信息见表3。

表3 尺寸优化前后位移和质量对比
尺寸优化后密封板结构较拓扑优化结构,变形量增加了0.4 mm,在可接受范围内。通过对计算结果进行分析可知,初始结构总质量为9.53 kg,最大位移为6.4 mm;尺寸优化后总质量为9.35 kg,最大位移为2.3 mm。其刚度提高了64%,质量基本保持不变。
接下来,对初始结构与尺寸优化后的密封板的应力大小及分布进行分析,计算结果如图17所示。

图17 初始结构与尺寸优化后结构应力对比
根据有限元计算结果可知,优化前最大应力为168.6 MPa,应力最大位置发生在螺栓孔位置处,即约束处;优化后最大应力为158.3 MPa,应力最大位置发生在螺栓孔位置处。二者均不超过材料的许用应力。
接下来,继续对优化前后的模态进行分析。目的是比较在优化前后,其固有频率的变化情况。其中,优化前密封板的前5阶振型及固有频率如图18所示。
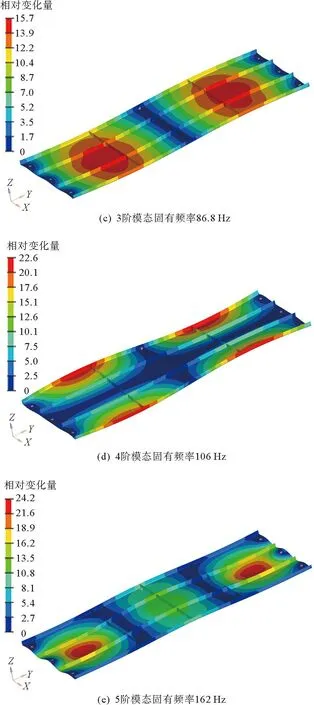
图18 优化前密封板前5阶模态
尺寸优化后密封板的前5阶振型及固有频率如图19所示。
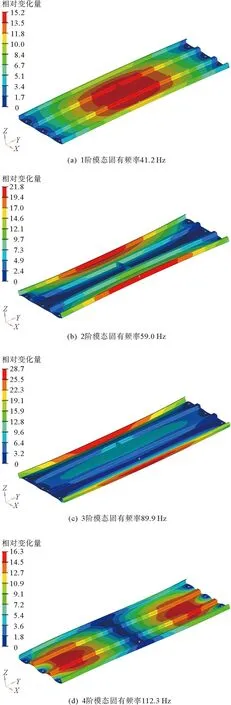
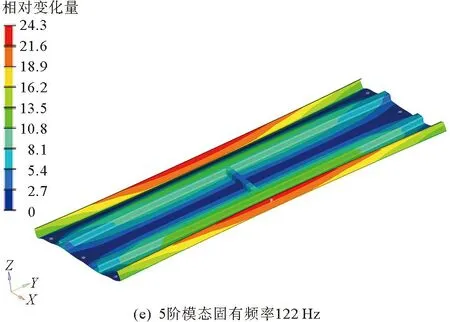
图19 尺寸优化后密封板前5阶模态
优化前后的固有频率对比见表4。

表4 尺寸优化前后固有频率对比 Hz
根据现场试验数据采集结果,测得列车在实际运行过程中,车下部分的气动载荷的固有频率在29 Hz附近,与初始结构的前两阶模态较接近。而尺寸优化后的密封板结构的最低固有频率为41.2 Hz,避免了气动载荷对结构产生的影响,提高了产品的使用寿命。
4 结论
通过对某型号列车的密封板进行拓扑优化分析和尺寸优化后得知,在总质量基本不变的前提下,密封板在优化前后的刚度提高了64%。且固有频率得到了较大的提高,1阶固有频率从23.8 Hz提高到41.2 Hz,避免了气动载荷对密封板结构的影响。这说明,通过拓扑优化方法寻求的最佳传力路径是有效的,结合尺寸优化设计方法能够在保证结构质量基本不变的前提下,最大化地利用材料,提高结构的刚度,从而为设计人员提供良好的设计思路。结合列车实际运行情况及工艺可行性方案可以降低产品的研发成本,提高产品的使用寿命,并缩短研发周期。
