基于改进鲸鱼算法的混合储能系统容量优化配置
2024-03-01吴成明扬臻辉
吴成明, 扬臻辉
(三峡大学 电气与新能源学院,湖北宜昌 443002)
0 引言
近年来,随着太阳能、风能等可再生能源在工程的广泛使用,此类能源的出力不确定性、随机性和间歇性成为了危害电网的重要问题。为了尽可能抑制上述问题,储能系统现阶段成为了微电网的主要组成部分[1-4]。由于混合储能系统的性能较好,在微电网中占主导地位。目前混合储能系统的制造成本昂贵,运行寿命较短且存在风光出力不确定性等问题。虽然储能系统容量越大,其平抑效果越好,但其制造成本更高,这二者之间是相互矛盾的。因此研究混合储能系统容量优化配置具有十分重要的意义[5]。文献[6]采用全寿命周期模型优化求解独立型风光互补储能系统的成本。文献[7]使用改进的粒子群算法来解决基于混合储能系统的全生命周期模型,但此改进算法的收敛精度较低,收敛速度较慢。文献[8]利用改进的鲸鱼优化算法求解混合储能系统的容量分配模型,但只以经济性最优为目标。上述文献均以经济性为单一目标进行研究,并未解决风电、光伏等可再生能源的不稳定性等问题。文献[9]提出一种平抑功率波动的储能容量优化配置方法,该方法考虑了系统的经济性以及限幅。文献[10]考虑联络线约束,对储能系统的经济成本进行了优化,但并未考虑联络线接入对容量配置的影响以及对成本的影响。文献[11]考虑到微电网的经济调度,但作者仅考察了传统的单一储能模型。文献[12]基于层次分析法,建立了用户侧多目标优化模型。文献[13-14]分别使用飞轮、超导储能技术,通过维持直流母线电压稳定来改善风电机组输出功率,但飞轮和超导储能技术并不成熟且成本较高。以上文献大多以成本最低为目标函数,仅有文献[9]考虑了可再生能源功率波动较大的问题,仅有文献[12]考虑了联络线接入电网利用率较低的问题。除此之外,在求解多目标优化问题时[15,16],常用的传统算法存在诸多弊端,如局部搜索能力差,容易陷入局部最优,搜索精度低,搜索速度慢等。
在上述研究的基础下,本研究在建立混合储能系统容量优化配置模型时,以成本经济性最优,可再生能源功率波动平抑效果最优,微网联络线利用率最高三个目标作为目标函数,采用改进鲸鱼优化算法、传统鲸鱼优化算法、传统粒子群算法[17]对该模型进行求解,最后对比三种算法求解出的容量配置方案来体现改进鲸鱼优化算法对该模型求解的优越性。
1 模型的建立
混合储能系统可以有效地平抑风光波动对电网造成的有害影响,在消除波动对电网的影响时还可以增加联络线利用率节约资源。在满足系统可靠性及经济性的运行条件下,配置混合储能系统应同时满足经平抑可再生能源功率波动最优、联络线利用率最高。本研究采用蓄电池组与超级电容器组作为混合储能系统的组件,模型如图1所示。

图1 微网模型
1.1 以经济成本最低为目标建立目标函数
(1)全生命周期成本(Life Cycle Cost,LCC)指产品在处于合理利用阶段时产生的与该产品利益相关的各种成本费用,主要包括设计成本、生产成本、购买成本、使用成本、维修保养成本、报废处理成本等。计算模型如下:
式(1)中:LCChess为全生命周期成本;Civ为设备的购置成本;Com为设备的运维成本;Cdc为设备的处置成本;Euc和Ebat分别为混合储能系统中超级电容器和蓄电池的容量;Ci1和Ci2分别为超级电容和蓄电池单位容量价格;Co1和Co2分别为超级电容和蓄电池单位功率的运行维护成本;Puc和Pbat分别为超级电容和蓄电池的功率;Cd1和Cd2分别为超级电容器和蓄电池的处理系数。
(2)以平抑可再生能源功率波动最优效果为目标建立目标函数f2,定义如下:
该系数采用经过混合储能系统作用后的可再生能源实际输出功率的差值总和与可再生能源实际输出功率之比来表征混合储能系统对风电功率波动的平抑能力。f2越大说明平抑能力越强,f2越小说明平抑能力越弱。式(2)中:i表示时段;PDG,i表示混合储能系统作用后的可再生能源功率;Pdg,i表示混合储能作用前的可再生能源实际发出功率;Pbat,i为蓄电池的实际输出功率;Puc,i为超级电容器的输出功率。
(3)以微网联络线利用率最高为目标建立目标函数:
联络线利用率定义为在一定时段内联络线实际功率的总和与联络线额定功率的总和的比值。联络线利用率在一定程度上反映了储能系统容量优化配置中联络线的使用情况。式(3)中:Egrid是联络线额定功率下输送的电量;Pgrid是联络线功率;Pgrid,0为联络线额定功率。
1.2 多目标函数处理
采用SAW法处理多目标函数,第一步为缩放,针对目标函数fi(x),已知其最大值和最小值采用缩放公式:
第二步为多目标函数的转化,将多目标优化模型转化为单目标优化模型求解,公式如下:
式中:λi为权重系数。
1.3 约束条件
为保证微网的运行可靠性,应满足以下约束条件:
式(6)代表功率平衡约束;式(7)代表混合储能系统约束;式(8)为联络线传输功率约束;式(9)为燃气轮机输出功率约束;式(10)为可再生能源功率约束。
2 改进鲸鱼优化算法
2.1 传统鲸鱼优化算法WOA
WOA由Mirjalili在2016年提出[18],该算法是模仿自然界中鲸鱼捕食行为的新型群体智能算法。鲸鱼捕食行为的目的是捕获猎物,一群鲸鱼在共同寻找猎物时,一定会存在某条鲸鱼先发现猎物的情况,这时其他鲸鱼一定会向这条发现猎物的鲸鱼游来争抢猎物。而鲸鱼的捕食行为主要分为三个阶段:包围捕食、收缩包围、螺旋捕食。下文所述公式具体见参考文献[18]。
2.1.1 包围捕食
在现实中,座头鲸能够识别猎物的位置并将其围成一圈。但在搜索空间中的最优位置是未知的,因此,WOA算法假设当前最佳候选解位置为目标猎物位置。在定义了目标猎物位置后,其他鲸鱼将尝试包围到目标猎物的位置。该过程的计算公式如下:
式中:X*(t)为最优解位置;X(t)表示当前解的位置;t为当前迭代次数;A、C为系数向量,由式(13)和式(14)确定。
式中:r1、r2为[0,1]之间的随机数;a在迭代过程中逐渐从2减小至0;T表示最大迭代次数。
2.1.2 泡网攻击
为了对座头鲸的泡网行为进行数学建模,设计了以下两种方法。
(1)收缩包围:通过减小式(15)中的收敛因子a的值来实现收缩包围,a的值随着迭代次数的递增而减小,当a减小时,A的波动范围也会减小。该机制本质上与保卫猎物阶段相同。
(2)螺线更新:鲸鱼个体在搜索猎物时采用螺旋上升的策略调整与猎物的距离,表达式如下:
式中:D'表示猎物与个体之间的距离;b为常数;l是[-1,1]的随机数。
为了同时模拟鲸鱼的收缩包围机制和螺旋更新机制,假设这两种机制执行的概率相等,可以用数学表达式表示如下:
2.1.3 搜索觅食
除了气泡网捕食法,座头鲸还会随机寻找猎物,当A>1时,在种群中随机选取一个个体寻优,不再追随参考鲸鱼,表达式如下:
式中:Xrand为随机一条鲸鱼的位置。
2.2 改进鲸鱼优化算法IOWA
2.2.1 Sine混沌理论的引入
传统鲸鱼算法的种群初始化采用个体位置伪随机化的模式,这种伪随机模式可以使整个种群在全部解空间上分布,但不一定能保证种群的均匀分布。
在WOA中,初始化鲸鱼种群位置的计算公式如下:
式中:Xi为个体i的位置;lb和ub是搜索空间的下界和上界;rand为[0,1]之间的随机数。
为增加种群多样性,为算法的全局搜索奠定基础,在算法初期引入Sine混沌理论,如式(21)所示:
式中:初始值xn不为0,且不在[-1,1]内产生不动点和零点。
2.2.2 引入新的自适应惯性权重
为提高算法的搜索精度和速度,引入一种在前期惯性权重大,后期惯性权重小的自适应惯性权重。公式如下:
当前期惯性权重大时,有较强的全局搜索能力。随着迭代次数的增加,w非线性递减,用以提高局部搜索能力,算法不断逼近最优解。式(22)中的k以初期的较小的值开始减小,避免算法前期就陷入局部最优,引入w后的位置更新公式如下:
2.2.3 非线性收敛因子
标准WOA的收敛因子a在迭代过程中是线性收敛的,而这种收敛模式与WOA算法的非线性搜索模式不对应,会造成局部搜索能力与局部开发能力的调节能力差,且非常容易陷入局部最优。因此设计一种非线性的收敛策略,改进后的a前期变缓慢,能够提高全局搜索能力,在算法后期,a迅速减小,能够提高局部搜索能力。在引入w后对a的改进公式为:
2.2.4 动态螺旋更新
标准WOA中的螺旋形状参数b设置为常数,使鲸鱼只能按固定的螺线线路进行搜索,寻优模式过于单一,极易陷入局部早熟。针对上述问题,设计一种动态更新的螺旋形状参数b,使鲸鱼群在进入螺旋搜索阶段后可以动态调节搜索的螺旋线路,增强了算法的全局搜索能力以提高算法的收敛精度。改进公式为:
2.2.5 变异交叉
为提高种群多样性,并增强算法的全局搜索能力与跳出局部最优的能力,在传统鲸鱼算法上引入了交叉变异理论。其步骤如下:
(1)种群初始化后,在种群中随机选择3个互不相同的目标向量Xi1,Xi2,Xi3,使用变异因子生成一个新的变异矢量,具体公式如下:
式中:F为变异因子,F∈[0,1],文中F取值为0.5。
(2)在变异操作生成变异向量后,即将变异向量与原目标向量进行交叉操作生成试验向量,二项式交叉定义如下:
(3)比较试验向量与目标向量的适应度值,适应度值高的向量进入下一代,判断公式如下:
式中:ffit表示适应度函数。
图2所示为算法流程图。
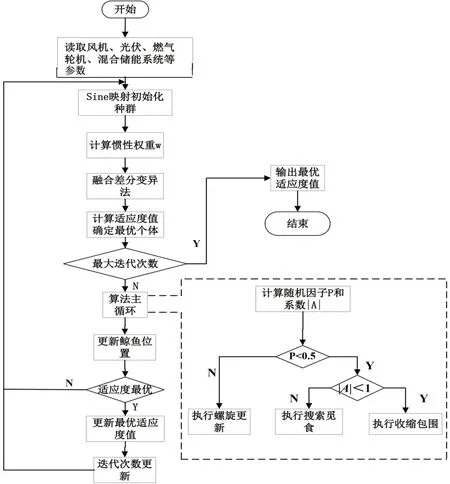
图2 算法流程
3 算例分析与仿真
选取我国某地并网型微电网作为研究案例,选取典型日的光伏及风电数据,采样周期为15 min,
混合储能系统的种组件为风机、光伏、微型燃气轮机,其输出的额定功率为别为80 kW、40 kW、50 kW。蓄电池与超级电容器参数如表1所示,风电、光伏及负荷的预测功率如图3所示。

表1 蓄电池与超级电容器参数

图3 典型日的光伏、风机及负载功率
(1)根据上述数据所建立的模型,分别采用IOWA算法,WOA算法和PSO算法进行模型求解,最后对比三种算法求解出的混合储能系统容量配置模型的配置方案,如图4及表2所示。

表2 PSO算法、WOA算法和IOWA算法的寻优结果
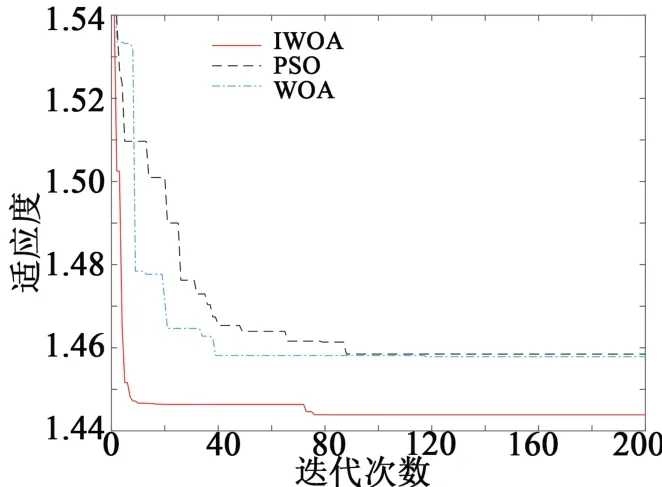
图4 PSO算法、WOA算法和IWOA算法的寻优效果
从图4可以得出PSO算法,WOA算法和IOWA算法均可以找到目标函数的最优值,然而,IWOA算法的表现优于WOA算法和PSO算法。从算法优化本身的性能来看,IWOA算法的收敛速度和收敛精度明显优于WOA算法和PSO算法。从表2可以得出在储能系统成本上,蓄电池和超级电容器用IWOA算法配置的成本较低。使用IWOA算法配置的电池和超级电容器的功率和容量较小,所以成本较低。与PSO算法相比,IOWA算法节省了115 882.6元;与WOA算法相比,IOWA算法节省了90 270.69元。从表征平抑可再生能源功率能力的可再生能源波动系数来看,IOWA算法与PSO算法和WOA算法相比提高了0.02。从微网联络线利用率来看IOWA算法比PSO算法提高了9.049%,比WOA算法提高了8.962%,微网联络线利用率的提高幅度非常大。综上所述,IOWA算法优于PSO算法和WOA算法,能够更好地得到混合储能系统容量配置方案。根据表2分析,在该案例配置混合储能系统容量时,应选择蓄电池功率为15.008 kW,应选择超级电容器功率为8.496 kW;应选择蓄电池的容量为123.036 kWh,应选择超级电容的容量3.411 kWh。最终得出混合储能系统的成本为651 324.1元,可再生能源的功率波动系数为0.025,联络线利用率为65.986%。通过对可再生能源功率波动平抑前后的比较,可以看出可再生能源功率得到了有效的平抑。优化后的仿真结果如图5所示。
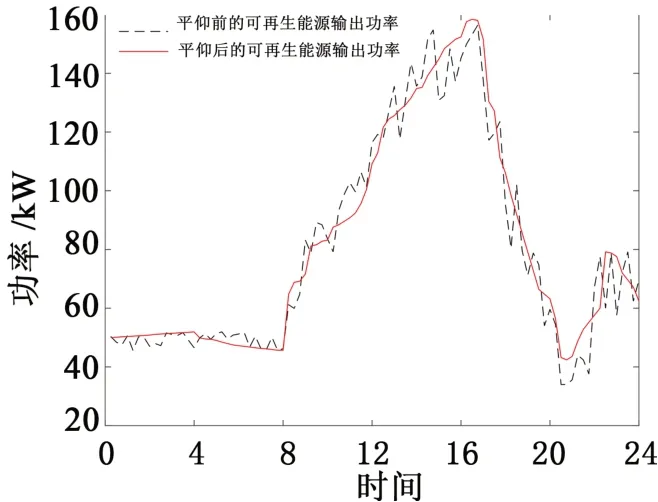
图5 可再生能源输出功率平抑效果对比
(2)为了验证在考虑微网联络线的利用率时将影响微电网混合储能系统的优化配置的想法,提出了一个比较方案。
仅考虑目标函数f1和f2,不考虑微网联络线利用率,建立混合储能系统的容量优化配置模型,并采用IOWA算法求解。最后与表2中的数据进行比较。比较结果见表3。
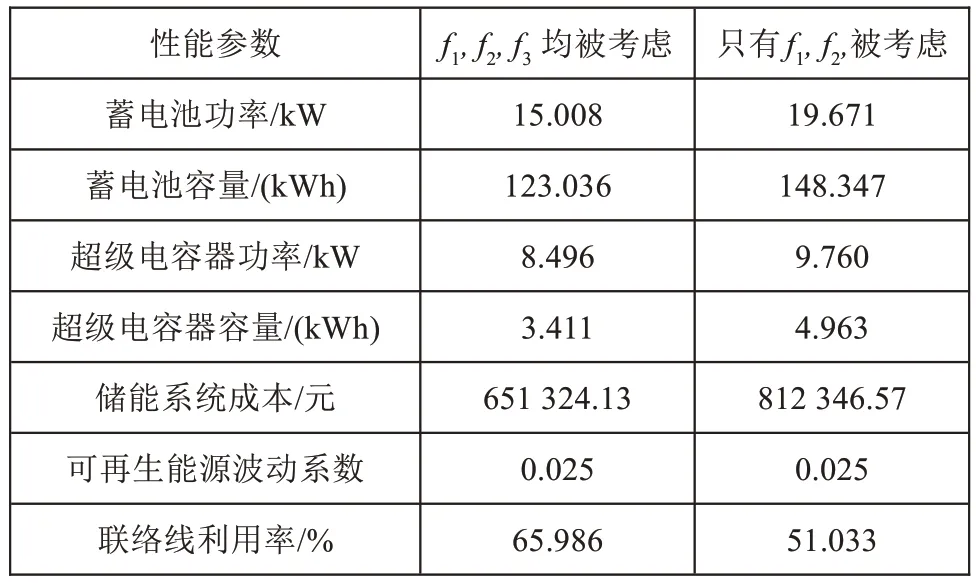
表3 两种模型的寻优效果
从表3可以看出,在考虑微电网混合储能的最优配置时,通过考虑联络线利用率,降低了混合储能的成本,同时联络线的利用率提高了14.953%。有效平抑了可再生能源功率波动,更加合理地利用了资源。
4 结束语
本研究建立的以混合储能系统的全生命周期成本、平抑可再生能源功率波动能力最优和微电网联络线利用率最高为目标的模型,用改进鲸鱼优化算法、传统鲸鱼优化算法、传统粒子群算法对模型进行求解,并通过并网型微电网的实例进行对比,得到了以下结论。
(1)储能系统的最优容量分配考虑了联络线的利用率,在考虑微电网混合储能的最优配置时,通过考虑联络线利用率实现了资源的合理利用,为大电网的资源分配提供了参考。
(2)改进后的IWOA算法相较传统PSO算法、WOA算法,收敛速度快,收敛精度高,搜索能力更强,易跳出局部最优。并通过算例验证了算法在混合储能系统的容量优化配置方面的优越性。
