挠性航天器姿态动力学数据驱动辨识与控制1)

陈竑宇 陈 提

(南京航空航天大学航空学院,南京 210016)

引言

姿态控制系统是航天器的重要组成部分.用于描述姿态运动的旋转矩阵的构型空间为Lie 群SO(3),由于不是欧几里得空间,为了便于姿态控制的研究,学者们提出了多种姿态表示方法[1].目前常用的姿态表示方法主要包括欧拉角,修正罗德里格参数(modified Rodrigues parameters,MRPs)和单位四元数等.但是这些姿态表示方法均有一定局限性,比如欧拉角和MRPs 存在奇异点,不能够全局描述姿态运动;而在单位四元数表示中,对于每一种旋转都存在两组单位四元数与之相对应,因此在姿态表示上并不唯一.所以,基于单位四元数的连续反馈控制率可能会产生不期望的退绕(unwinding)现象[1-2].因此,已有许多研究尝试直接在SO(3)上解决姿态控制问题.在SO(3)上刚体姿态动力学由12 个非线性方程描述,但通常有3 个控制输入,是典型的一个多输入多输出非线性系统.Lee 定义了一个新的姿态误差函数,并设计了指数稳定控制器[3].Sanyal等[4]讨论了由旋转矩阵描述的刚体姿态估计和控制问题.由于时不变光滑反馈律最多仅能保证SO(3)上姿态控制的近全局收敛,Berkane 等[5]提出了一种基于中心协同混合方法的全局指数稳定控制方案.Wang 等[6]研究了角速度为分段正弦信号的SO(3)的姿态控制.在实际工程中,航天器通常带有挠性构件,因此不能忽略挠性振动与姿态运动的耦合关系,龚柯杰[7]将航天器挠性附件振动视作外界扰动项,并设计了自适应滑模控制器.He 等[8]使用假设模态法建立SO(3)上挠性航天器姿态动力学模型,提出了一种迭代学习观测器用于观测噪声,并基于观测器设计了一个复合控制器来稳定姿态.在这些研究中,控制器设计完全或部分取决于建模,但挠性航天器姿态动力学通常具有强非线性、强耦合、参数不确定性,模态测量困难等特点,此外,大尺寸挠性航天器存在模态集中和“全局运动叠加全局模态”等复杂现象[9],因此,建立挠性航天器精确动力学模型是一个极其困难的任务.

对于复杂的非线性系统,为了分析的方便,往往会考虑将其线性化.典型的方法包括泰勒线性化、分段线性化和正交函数逼近线性化等.但这些方法存在明显局限,泰勒线性化只在工作点附近进行,分段线性化需要更多模型信息,正交函数逼近线性化计算量大且控制器设计复杂.1931 年,Koopman[10]提出非线性动力系统可以通过作用于测量函数上的无限维线性算子表示,即提出了一种非线性系统的全局线性化方法.随着近些年计算机技术和大数据的发展,Koopman 算子理论被越来越多地运用于复杂非线性系统行为分析[11-14].一些研究已经提出了一些低阶非线性系统的解析观测函数集[12,15],但对于更复杂的非线性动力学或者未知动力学系统,则难以解析地得到Koopman 算子的表示.因此可以采取数据驱动方法被辨识Koopman 算子,这种方法在建模过程中只需要仿真或者实验数据,而不像传统方法那样依赖于物理参数.由于Koopman 算子通常是无限维算子,在实际应用中往往需要得到其有限维截断.Schmid[16]在流体动力学领域提出了动态模态分解算法(dynamics mode decomposition,DMD),随后Rowley 等[17]在DMD 和Koopman 理论之间建立了重要联系.目前,辨识Koopman 算子常用的算法包括DMD 算法[16]和拓展动态模态分解(EDMD)算法[18]等.Dahdah 等[19]针对现有算法辨识开环系统Koopman 算子的局限性,结合输入输出子空间辨识法和EDMD 算法得到了闭环系统Koopman 算子.由于DMD 算法和EDMD 算法直接计算Koopman算子有限维截断,截断误差会不可避免影响建模精度.Brunton 等[20]提出非线性动力学的稀疏性辨识(SINDY),通过稀疏回归算法精确辨识非线性动力学的广义线性模型.Kaiser 等[21]在少量数据基础上基于SINDY 算法辨识非线性动力学,验证了SINDY算法的准确性,并基于模型使用非线性模型预测控制器(NMPC)实现系统控制.

近年来,许多研究人员开始关注基于Koopman算子理论的非线性系统控制问题,将成熟的线性控制理论用于解决非线性系统控制问题.Kaiser 等[22]基于一些低阶非线性系统,讨论了基于Koopman 算子的控制问题.Ren 等[23]基于Koopman 理论设计了轮式机器人的滑模控制器.Korda 等[24]在Koopman算子理论的基础上采用线性模型预测控制对非线性系统进行控制.为提高闭环Koopman MPC 的鲁棒性,Zhang 等[25]提出一种基于Tube 模型预测控制(tube-based MPC)的鲁棒Koopman 控制器.Goyal 等[26]提出了一种基于Koopman 算子和数据驱动方法的三自由度腕部康复机器人的轨迹跟踪控制器.

目前也已有一些研究将Koopman 算子理论用于SO(3)上的姿态控制.比如,Chen 等[27]基于SO(3)构型提出了一组非线性观测函数,得到了SO(3)上姿态动力学Koopman 算子的解析表示,并在此基础上设计了最优控制器.Zinage 等[28]考虑了刚体位姿控制,将Koopman 建模的研究推广到SE(3)群上的无人机动力学.这些研究主要是针对刚体姿态动力学的建模与控制,但由于实际中航天器带有挠性构件,不能忽略挠性振动与姿态运动的耦合关系,因此SO(3)上挠性航天器姿态动力学的Koopman 辨识会更加复杂.

本文拟提出一组观测函数用于Koopman 算子的数据驱动辨识,这组观测函数仅依赖于状态测量数据,而不需要任何先验信息.在此基础上,本文基于SINDY 算法得到SO(3)上挠性姿态动力学的稀疏化广义线性模型和Koopman 算子的有限维截断,实现对挠性航天器姿态动力学的全局线性化建模.基于截断的Koopman 算子设计一种高效率的线性LQR 控制器,在实现挠性航天器姿态控制的同时抑制挠性构件振动,最后通过仿真算例验证所提出的数据驱动建模方法和最优控制器,并和传统最优控制方法进行对比以论证所提方法的优势.

1 数据驱动建模

1.1 Koopman 算子理论

Koopman 算子理论可以将有限维非线性系统转换为无穷维线性系统.考虑如下非线性动力系统

式中x∈S为光滑流形上的N维线性系统的状态,S⊆RN为状态空间.

定义实值观测函数g:M→R,它是Hilbert 空间上的元素.Koopman 算子 Kt是一个无限维线性算子,它对测量函数g的作用如下

其中 ◦ 为合成算子.

若式(1)中系统变为离散时间形式,那么对于时间步长为 Δt的离散时间系统x(k+1)=FΔt(x(k)),式(2)变为

即,Koopman 算子定义了一个无限维线性动力系统,并使状态观测值gk=g(xk) 推进到下一时间步长,即测量函数的演化[29].

Koopman 算子的线性属性来源于观测函数空间中加法运算的线性,即

其中 α1,α2为常数.

Koopman 算子定义了一个无穷维线性系统来表示非线性系统,但无穷维的性质会给Koopman 算子的应用带来问题.在实际应用中,无穷维系统通常可以被截断,如果不产生过大的精度损失,那么就可以通过有限维线性系统来近似Koopman 算子.

1.2 SO(3)上挠性航天器姿态动力学建模

SO(3)上的刚性航天器姿态动力学方程可表示为如下形式

其中R∈S O(3) 表示从航天器体坐标系到惯性参考系的旋转矩阵,ω ∈R3是体坐标系的角速度,J∈R3×3为航天器惯性矩阵.对于任意向量a∈R3,a×定义为

在本文研究中,假设挠性航天器的结构为中心刚体上固接梁,其构型如图1 所示.可采取假设模态法对挠性航天器进行建模.SO(3)上的挠性航天器姿态动力学方程可以写为式(5)以及如下方程

图1 挠性航天器示意图Fig.1 Flexible spacecraft

考虑到挠性构件模态坐标一般不能直接测量,但可以测量挠性构件上各点位移以及速度.挠性构件位移w以及速度与模态坐标q和之间的关系为

其中,Φ∈RN×m为各模态对应固有振型矩阵,N为传感器数量,且N＞m.因此,可以使用替代模态坐标参数,两者之间关系为

1.3 非线性动力学稀疏性辨识

原始SINDY 算法[20]主要思想是利用非线性动力学中通常只包含少数起作用项的性质,从人工选取的字典函数库中寻找动力学中的有效项.考虑如下受控非线性动力学系统

收集时序数据得到数据快照矩阵

建立候选非线性函数库

其中 θi为人工选取的候选非线性函数,以保证Θ(X,U) 中包含非线性动力学f(x,u) 中的有效项.通过以下广义线性模型来逼近非线性动力学f(x,u)

式中,Ξ 的列向量 ξk是一个系数向量,用于确定动力学中的有效项,且 ξk中的非零项要尽可能少.通过稀疏回归算法辨识动力学对应有效项

将系统原始状态映射到高维观测函数空间,再辨识观测空间中动力学的有效项,便可以得到在观测函数空间上非线性动力学的广义线性模型,其中的线性部分便能作为Koopman 算子的有限维截断.

选取构成Koopman 提升空间的非线性观测函数 Ψ ∈RN和控制耦合函数 Ψu∈RM以及高阶补偿观测函数如下

基于数据可得到提升的数据快照矩阵为

通过稀疏回归算法可以得到提升空间上的广义线性模型如下所示

为了后续讨论方便,将非线性系统的近似广义线性模型,即式(25),写为状态空间形式,即

即得到非线性动力学Koopman 算子的有限维截断.

目前常用的稀疏回归算法包括套索回归(LASSO)或者序贯阈值最小二乘(sequential thresholded leastsquares,STLS)等[20].本文采取序贯阈值最小二乘算法(STLS)来计算SINDY 模型.STLS 算法基本思想是以稀疏提升系数为阈值将最小二乘解稀疏化,其具体计算过程如下:

(3)将 Ξ 中所有小于稀疏提升系数 λ 的系数置零.矩阵Bi表示 Ξ 中非零元素位置,其中非零项对应位置元素为1,其他位置元素为0;

(4)通过最小二乘法重新计算稀疏最优拟合算子 Ξ,但是将仅使用非稀疏项所对应的数据,即ξk=,其中 ξk为 Ξ 的第k列,Bik为Bi的第k列,·为点乘运算;

(5)重复步骤(2)～ (4),直到达到最大迭代步数或者解收敛.

2 控制器设计

对于线性系统,其性能泛函是状态变量和控制变量的二次型函数的积分,则这样的最优控制问题称为线性二次型最优控制问题,线性二次型调节器(LQR)可以得到状态线性反馈的闭环最优控制率[30].由于求解方便,LQR 的使用非常广泛,是现代控制理论中最重要成果之一.Koopman 算子理论可以将本文所关心的挠性航天器的非线性控制问题映射到线性控制,因此可以采用LQR 方法设计相应的控制策略.本节基于SINDY 辨识得到的Koopman 算子有限维近似模型,提出了一种LQR 控制器,在后续内容中称其为Koopman-LQR 控制器.

其中QLQR和RLQR为正定矩阵.Koopman-LQR 控制增益F可以通过求解代数Riccati 方程得到

Koopman-LQR 控制输入便可以写为

注意到Koopman-LQR 控制输入 ΨuLQR需要进行逆变换才能得到实际输入到挠性姿态动力学系统中的控制力矩,且根据非线性观测项的选择不同,Ψu可能为状态依赖量.因此需要通过状态依赖转换矩阵T(x) 计算实际输入的控制力矩u,如下所示

其中T(x) 为将u映射到 Ψu的变换矩阵,其形式基于Ψu的选取,上标 † 表示伪逆.变换矩阵T(x) 通常可以基于上一采样时刻的状态测量计算得到.

3 观测函数选取

Chen 等[27]提出了一组观测函数,并解析得到了SO(3)上刚性航天器姿态动力学的Koopman 算子,但是所提出的观测函数并不适用于挠性情况,且所提观测函数中控制输入的计算要求已知航天器转动惯量矩阵.本文根据挠性航天器姿态动力学所包含的非线性成分,提出了一组用于SINDY 算法辨识SO(3)上挠性航天器姿态动力学Koopman 算子有限维截断的非线性观测函数.

对于带挠性构件的航天器姿态动力学,非线性观测选取为如下

因此,基于Koopman 算子理论,在小角速度情况下,挠性航天器姿态动力学可近似地表示为

由于同时需要足够大的阶数保证线性化系统有足够的精度,以及避免观测函数项过多而产生较大的回归误差,在之后的仿真中都将式(33)～ 式(37)中的观测函数阶数n取为3.

4 仿真分析

在仿真算例中,假设有3 个模态与航天器转动耦合,其他模态和转动的耦合系数均为零,并且假设挠性构件上有3 组位移和加速度传感器,即模态振型矩阵 Φ 可逆,则1.2 节中式(11)成立.

4.1 数据获取

SINDY 是一种数据驱动算法,因此需要采集训练数据.基于1.2 节中的挠性航天器姿态动力学数学模型,在MATLAB 中使用ODE45 进行数值仿真,将所得仿真数据作为训练数据.假设有3 个模态与航天器转动耦合,只给出前3 阶模态参数.挠性航天器的参数如表1 所示.

表1 航天器参数Table 1 Parameters of spacecraft

数据的采样间隔取为0.01 s,初始条件为: 随机的初始旋转矩阵R(0) 和随机初始角速度ω(0)∈[-0.01,0.01] rad/s,挠性构件初始模态坐标参数为q(0)=0,(0)=0 .将控制力矩设为如下形式的正弦激励

其中aj∈[0,1],bj∈[0,2],cj∈[0,2π],j=1,2,3,Amp=0.1.

将在以上随机初始条件和控制力矩下得到的160 组,时间为4 s,数据长度为401 的状态轨迹用作训练数据.SINDY 算法所需要的导数数据由五点法数值微分得到,因此实际上训练数据为160 组数据,每组包含396 组采样.

4.2 挠性姿态动力学SINDY 模型

取SINDY 算法中稀疏提升系数为λ=1×10-5.基于数据得到SINDY 模型,并使用均方根误差来评估模型对训练数据的拟合程度

其中‖ ‖2表示矩阵的2 范数.

SINDY 模型对训练数据的均方根误差为RMSEtrain≈1.2×10-9.另外将40 组长度4 s 的随机初始条件出发的采样数据作为验证数据集,模型对验证数据集的均方根误差为RMSEverify≈1.5×10-9.结果表明SINDY 模型对训练数据的拟合精度高,且具备良好的泛化能力.

为验证数据驱动模型的预测精度,进行20 组随机初始条件下的仿真,其结果与数值解的误差表示了模型预测精度.由于需要验证挠性构件存在初始振动的情况下的数据驱动模型的预测精度,将初始模态坐标设为非0,其范围如下

角速度预测误差由角速度中各个元素的平均误差Errω来表示

旋转矩阵预测误差由旋转矩阵中各个元素的平均误差ErrR来表示

挠性航天器姿态动力学SINDY 模型的50 s 内的预测误差如图2 所示.图2(a)显示角速度预测误差在大约 ±1.6×10-5rad/s 范围内,图2(b)显示50 s内旋转矩阵预测误差在 ±1×10-3范围内.

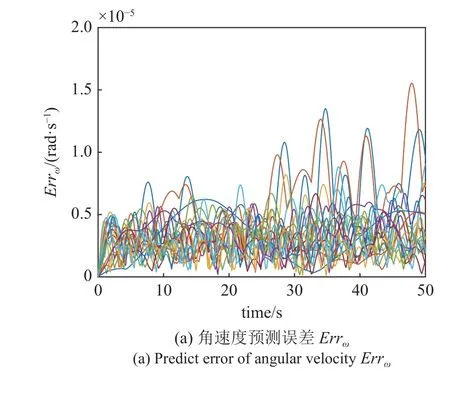
图2 SINDY 模型预测误差Fig.2 Predict error of SINDY model

结果表明SINDY 算法准确辨识到了姿态动力学系统在提升空间中对应的非线性成分,证明了数据驱动建模的有效性.而对于挠性航天器姿态动力学Koopman 算子有限维截断,即式(27),也需验证其预测能力.Koopman 算子有限维截断的预测误差如图3 所示,结果表明由于忽略了更高阶非线性项成分,误差相对SINDY 模型有明显增大.

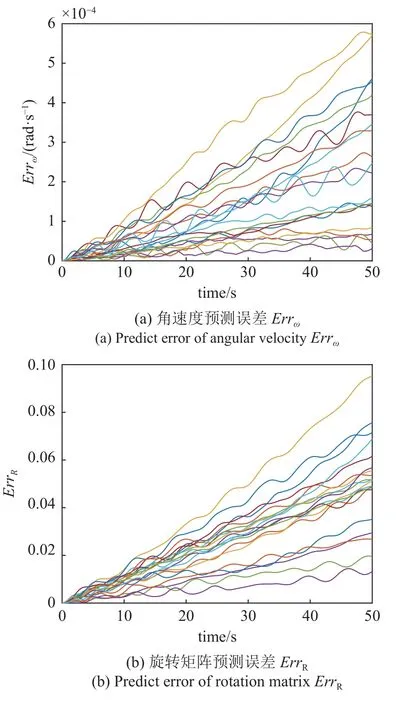
图3 Koopman 模型预测误差Fig.3 Predict error of Koopman model

由于回归误差和软件计算误差等因素,SINDY模型不能完全精确地得到非线性动力学中有效项的系数,特别是其对应系数小的情况,这是影响模型精度的主要原因.事实上,非线性函数项越多,在回归过程中产生的误差越大.注意到无论是SINDY 模型还是截断的Koopman 算子,其角速度的预测精度都要好于旋转矩阵的预测精度,这是由于表示旋转矩阵的非线性观测项要多于表示角速度的项,并产生了相对更大的回归误差.因此,简单地增加更多观测函数项并不一定能够提高模型精度.

4.3 挠性姿态动力学Koopman-LQR

基于4.2 节得到的线性化模型,根据第2 章内容设计LQR 控制器.本节中仿真的采样间隔设为0.2 s,在Koopman-LQR 作用下,进行20 组时长为200 s的随机初始条件出发的仿真.

Koopman-LQR 控制器的代价函数参数可以写为如下形式

其中权重矩阵QR,Qω,Qw对应旋转矩阵R,角速度ω和挠性件位移 δ,QRω对应R和 ω 耦合项,RΨu对应控制耦合观测 Ψu.根据第3 章中的观测函数的选取,令QR=100I9,Qω=20 000I3,QRω=0,Qw=1000I6,RΨu=I138.

定义姿态误差指标函数为

定义挠性构件振动的指标函数为

其中,q为模态坐标,m为模态坐标的数量.

20组仿真结果如图4 所示,图4(a)为姿态跟踪误差,结果表明在不同初始条件下Koopman-LQR 控制器均能在120 s 内将挠性航天器姿态误差V1控制到 1×10-3范围内.图4(b)显示Eq在40 s 内快速减小到0.1 内,其中子图表明挠性构件振动在大约100 s前被抑制到很小范围内.仿真结果表明在SINDY 辨识的Koopman-LQR 控制器能够将航天器姿态有效控制到目标姿态,并且抑制住挠性振动.

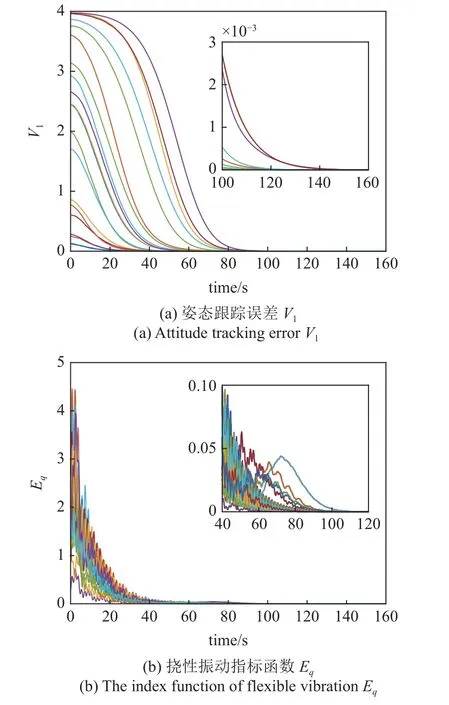
图4 随机初始条件下的20 组仿真Fig.4 20 simulation results with random initial condition

仿真使用的计算机处理器为Intel i7-11700.在仿真过程中,Koopman-LQR 控制器平均单步所需计算时间大约为1.7 ms,实际上可以采用更高的采样频率.

此外,为了解代价函数参数对Koopman-LQR 控制器性能的影响,从同一初始条件出发,对比不同代价函数参数的Koopman-LQR 作用下的结果.共7 种不同的QLQR和RLQR的选取方案,如表2 所示,其中情况3 与先前的仿真中的选取一致.从相同的初始条件出发进行仿真,姿态跟踪误差V1如图5(a)所示,挠性构件振动指标函数Eq如图5(b)所示.

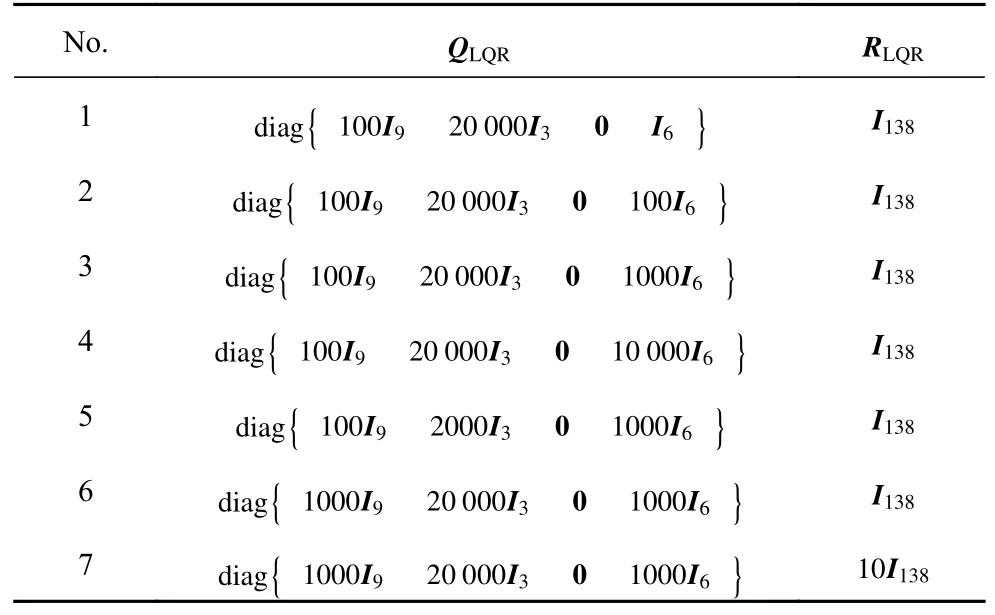
表2 不同的 QLQR 和 RLQR 选取Table 2 Different chosen of QLQR andRLQR

图5 不同 QLQR 和 RLQR 对Koopman-LQR 姿态控制的影响Fig.5 Influence of different QLQR andRLQR

观察图5(a) 和图5(b),表2 中情况3 与情况6 比较表明,增大QLQR中旋转矩阵元素对应权重系数可以减小控制时间;情况3 和情况5 对比表明增大QLQR中角速度 ω 对应权重系数,能够限制控制器的响应速度,获得更平滑的控制效果,但意味着需要更多时间才能控制到期望姿态.通过选取不同的RLQR可以调节控制时间,但如图5(a)中情况6 和情况7 所示,RLQR过大可能会导致控制器出现超调现象.从图5(c)可以看出,情况1,2,3 在100 s 时挠性构件振动显著大于情况4,这意味着增大QLQR中挠性构件模态坐标对应参数能增强Koopman-LQR的振动抑制能力.

除了进行姿态控制,在协同或同步任务中,挠性航天器往往需要与目标航天器或相邻航天器的运动同步,这就需要控制器既能够高精度地跟踪预定轨迹,也能够抑制挠性构件的振动.因此对本文所提控制器跟踪时变期望姿态的情况进行仿真.

假设期望姿态的轨迹为满足初始时刻姿态为R(0)=I3的刚性航天器运行轨迹,其角速度满足如下方程

挠性航天器初始姿态矩阵为I3,初始角速度为rad/s,初始模态坐标为q=0,=0 .实际上,姿态跟踪性能也受到代价函数参数的影响.将LQR 代价函数参数选取为表2 中的其中情况,分别进行长度为500 s 的仿真.

跟踪时变期望姿态的仿真结果如图6 所示,图6(a)为角速度 ω1的跟踪误差,而图6(b)为旋转矩阵的跟踪误差.结果表明,在不同的代价函数参数选取情况下,Koopman-LQR 能够很好地抑制振动并跟踪期望姿态,姿态跟踪误差大约在 [0,2.5×10-3] 范围内,而角速度 ω 中第一个元素 ω1的跟踪误差大约在±2×10-3rad/s范围内.

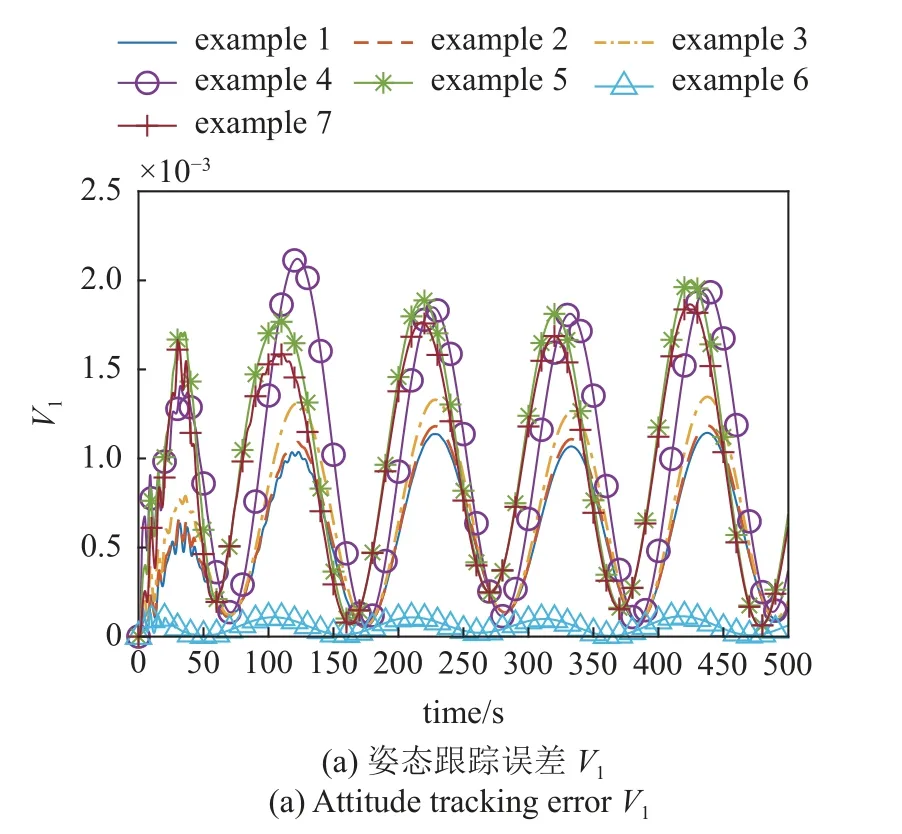
图6 不同代价函数参数 QLQR 和 RLQR 对Koopman-LQR 姿态跟踪效果的影响Fig.6 Influence of QLQR and RLQR on attitude tracking

将图6 中情况1,2,3 和情况4 的结果相对比,发现挠性构件参数 δ 在代价函数中权重越高,振动抑制效果越好,但姿态跟踪误差增大.将情况3 与情况5 以及情况6 的对比发现,QLQR中旋转矩阵和角速度 ω 对应权重系数越大,姿态跟踪误差越小.

以上姿态控制和姿态跟踪的两个算例说明了Koopman-LQR 控制器的计算效率较高,且具有不错的控制精度.但由于代价函数中参数的选取对所提控制器性能的影响比较大,需要根据需求选取合适的代价函数.

4.4 Koopman-LQR 与传统最优控制对比

为了评估本文所提控制器的控制器性能,将Koopman-LQR 控制器与状态依赖Riccati 方程(SDRE)控制器进行对比.SDRE 控制器最初用于解决仿射非线性系统控制问题,作为线性LQR 控制理论在非线性系统上的推广,其简化了非线性优化问题中HJB (Hamilton-Jacobi-Bellman)方程的求解,避免了求解两点边值问题[31].

对于SO(3)上挠性姿态动力学,通过在每一时间步迭代求解离散时间形式的状态依赖仿射系统的Riccati 方程得到全状态反馈控制率.为了对比,令SDRE 代价函数与Koopman-LQR 代价函数形式相同.SDRE 控制器的具体设计见附录.

从同一初始条件出发,采样间隔为0.2 s,进行时长200 s 的仿真.SDRE 控制器与Koopman-LQR 的前120 s 仿真结果对比如图7 和表3 所示.其中图7(a)为姿态跟踪误差V1,图7(b)为式(44)中定义的挠性振动指标函数Eq.另外,将跟踪时变期望姿态情况下Koopman-LQR 和SDRE 的性能进行对比,初始条件和期望姿态取为与4.2 节中一致,过程中的最大姿态跟踪误差如表3 所示.

表3 Koopman-LQR 与SDRE 结果对比Table 3 Comparison between Koopman-LQR and SDRE

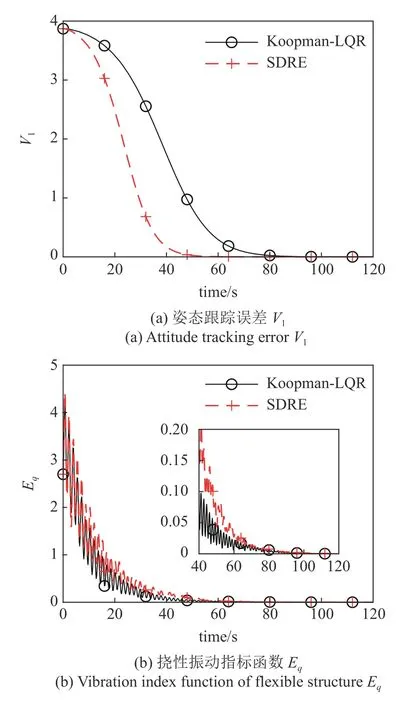
图7 Koopman-LQR 与SDRE 的对比Fig.7 Comparison between Koopman-LQR and SDRE

图7(a)和图7(b)表明在两种控制器代价函数J形式相同的情况下,SDRE 控制器与Koopman-LQR的效果比较接近,SDRE 控制器相对更快地将挠性航天器控制到期望姿态.表3 结果表明SDRE 跟踪时变姿态的姿态误差要小于Koopman-LQR.而图7(c)表明Koopman-LQR 对挠性振动的抑制要好于SDRE.在计算效率方面,SDRE 控制器共用时约17.9 s,Koopman-LQR 共用时约1.7 s,这是由于SDRE 控制器在每一采样间隔内都需要求解代数Riccati 方程,使得其计算效率相对更低.表3 中第3 行是跟踪时变期望姿态情况下的最大姿态跟踪误差,结果表明Koopman-LQR 和SDRE 均能够使以较高精度使航天器跟踪期望姿态.由于在线求解最优控制的缘故,SDRE 的姿态跟踪的精度相对更高.

综合来看,不像SDRE 那样需要对航天器姿态动力学进行精确建模,Koopman-LQR 只基于数据驱动辨识模型进行设计,虽然相较于SDRE 控制器控制精度有所不如,但是Koopman-LQR 具有计算效率更高和对挠性振动的抑制效果更好的优势.

5 结论

本文提出了一组观测函数用于数据驱动辨识得到SO(3)上挠性航天器姿态动力学的Koopman 算子的有限维截断.观测函数构建为旋转矩阵与姿态角速度及其部分耦合项,还包括挠性构件测量点位移与加速度和它们与姿态角速度和旋转矩阵的耦合项.基于SINDY 算法,通过拓展观测项和引入高阶补偿项来得到提升空间上的挠性航天器姿态动力学的广义线性模型和截断Koopman 算子.使用SINDY模型,可以以较高精度预测航天器状态轨迹,而其线性部分即截断的Koopman 算子也能在一定时间内以一定精度预测系统未来状态.此外,基于Koopman算子理论设计了一个LQR 控制器,能够实现挠性航天器姿态控制以及振动抑制,且该控制器能够以较高的计算效率实现接近最优的控制效果.

未来将考虑数据存在噪声和航天器存在外界扰动(如重力梯度力矩)的情况,并尝试将数据驱动方法与Koopman 理论用于航天器集群控制等领域.

附录A SDRE 控制器

考虑如下非线性系统

将上式写为控制仿射形式,即

其中,f(x)=A(x)x.上述控制仿射形式方程具有如下形式的无线时间性能函数

为了确保局部稳定,对于任意x,Q(x) 须为半正定矩阵,R(x)为正定矩阵.上式可以看作线性LQR 方法在非线性控制里的推广.若P(x) 是满足如下状态依赖代数Riccati 方程(SDRE)的正定解

则控制输入可以表示为

在每一采样间隔内,将状态依赖系统视为线性时不变系统,便可通过求解时不变代数Riccati 方程得到控制量.

其中u∈R3为控制力矩,,J为航天器转动惯量矩阵.在A(x) 和B(x) 中

其中rij为旋转矩阵R的元素.

其中

其中Jij为航天器转动惯量矩阵J的元素.

其中m为模态坐标数量,K为模态刚度矩阵,C为模态阻尼矩阵.

SDRE 控制代价函数形式为

为保证SDRE 的代价函数与Koopman-LQR 一致,且注意到Koopman-LQR 的控制量是在观测函数空间的,因此对应的控制代价参数需要进行相应变换,即令其中为从u到 Ψu的状态依赖变换矩阵.在小角速度情况下,有另外,由于在Koopman 建模中采用的是挠性构件位移w,而本节中状态依赖控制仿射系统使用模态坐标q,因此也需进行变换以保证代价函数x形式一致.由于有,则

其中P(x) 是满足如下方程的正定解