非线性拉伸对层流燃烧速度提取的影响

2024-03-01蔡骁张龙凯王金华黄佐华

中南大学学报（自然科学版） 2024年1期

蔡骁，张龙凯，王金华，黄佐华

(西安交通大学动力工程多相流国家重点实验室，陕西西安，710049)

层流燃烧速度是衡量可燃混合气扩散性和反应性最重要的物理化学参数，是研究预混燃烧问题的关键因素[1-2]。它经常被用来验证化学反应动力学机理的准确性，同时还是研究火焰动力学的基础[3]。在实际内燃机燃烧过程中，层流燃烧速度在确定一些重要参数中起到关键作用[4]，例如：1) 混合气最小点火能量，决定发动机能工作的当量比范围；2) 淬熄距离，影响未燃碳氢和一氧化碳的主要排放来源；3) 着火延迟，影响点火提前和缸内循环变动。在大部分湍流燃烧模型中，层流燃烧速度都是一个重要的输入参数。在基础研究中，层流燃烧速度、着火延迟时间、物种浓度曲线、熄火极限等是验证和发展化学动力学模型的重要实验参数。不管是确定汽油机中重要参数，发展准确湍流燃烧模型，还是验证化学动力学模型，都需要提供准确可靠的层流燃烧速度数据。层流燃烧速度的测量装置有很多种，目前比较常用的测量方法有本生灯火焰、平面火焰、对冲火焰和球形传播火焰[2]。在这些方法中，球形传播火焰被证明是一种简单有效的手段，特别是在其他方法难以达到的高压条件下(1～6 MPa)，仍然可以方便地测量层流燃烧速度[2]。虽然层流定容燃烧弹结构简单，但测量层流燃烧速度时仍然会受到很多因素的影响[5]。如前期点火的影响[6]，后期腔体的影响[7]，中间辐射热损失[8]、火焰不稳定性[9]和火焰拉伸的影响。其中拉伸对火焰传播速度有着强烈的影响，因此只有消除拉伸的影响才能获得准确的层流燃烧速度。

拉伸率随火焰传播是不断变化的，需要建立拉伸率和火焰传播速度之间的关系，然后将拉伸率外推至零得到无拉伸火焰传播速度，最后通过质量守恒方程进行密度修正，进而得到层流燃烧速度。早些年，普遍认为拉伸率和火焰传播速度之间存在着简单的线性关系。最近几年通过实验、理论和模拟研究发现火焰传播速度随拉伸率成非线性的变化[1]。KELLEY等[10-11]系统性研究了非线性拉伸的影响，发现由于非线性拉伸的影响，采用线性外推方法提取结果会明显高于非线性外推方法。随后的研究在不断尝试提高非线性外推方法的测量精度和适用范围[12-16]。目前几种不同的速度外推方程在实验研究中都得到了应用，而实验测量层流燃烧速度的系统误差主要来源是外推方程和火焰半径范围的选取。CHEN等[17-19]分别用模拟和实验的方法比较了几种常用外推方程的表现。发现这些模型都具有一定的局限性，只有在比较有限的范围内能获得准确的实验结果。因此，需要获得一种精度更高、适用范围广的层流燃烧速度外推方程。

本文研究目的是获得更准确的层流燃烧外推方程，并对该外推方程和文献中常用的3种外推方程进行评估。为此，本文作者采用定容燃烧容弹结合高速纹影摄像系统获取甲烷/空气、正丁烷/空气和氢气/空气的火焰传播历程，并且选取合适的火焰半径范围消除或减小其他因素的影响，研究非线性拉伸对层流燃烧速度提取的影响。利用实验测量结果对文献和本文的4种外推方程进行评估，并基于不同方程的表现，提出减小非线性拉伸影响的方法，进而获取更加准确的层流燃烧速度。

1 层流燃烧速度外推方程

球形传播火焰外推方法是采用不同的线性或非线性外推方程从火焰传播历程中获取层流燃烧速度的过程。下面分别介绍几种常用的线性和非线性的外推方程。早期大部分实验测量都采用如下的线性方程[20]：

其中：K为火焰拉伸率，A为火焰面积；rf为火焰半径；t为时间；Sb为火焰传播速度，Sb=drf/dt，可以由实验直接测量；S0b和Lb分别为无拉伸火焰传播速度和马克斯坦长度。Lb主要描述火焰传播速度对火焰拉伸率的依赖程度，还能表征质热扩散不稳定性对火焰的影响程度。层流燃烧速度SL可由方程ρuSL=ρbS0b计算得到，其中，ρ表示气体密度，下标u和b分别表示未燃气和已燃气，上标0表示无拉伸状态，即K=0。

FRANKEL等[21]通过对球形传播火焰进行理论研究得到相对于火焰弯曲κ=2/rf的线性方程(相对于拉伸率是非线性方程)：

值得注意的是该方程最初是MARKSTEIN在1951年通过实验测量，并从现象学的角度提出[17]。后来FRANKEL等[21]采用渐近理论从理论上证明了该结论。

KELLEY等[10]基于RONNEY等[22]的理论研究，假设球形火焰传播处于一种准稳态传播的状态，忽略非稳态项后得到如下非线性方程：

RONNEY等[22]以及KELLEY等[23]对球形传播火焰进行了理论分析，得到如下原始理论方程：

理论方程(4)能适用于大路易斯数(Le)和强拉伸情况，Le定义为混合气的热扩散系数和不足反应物的质扩散系数之比，即Le=α/D。但理论方程(4)是数值不稳定的，由于存在发散项导致无法直接用于实验测量层流燃烧速度。非线性方程(3)即由理论方程(4)忽略非稳态项(右边第一项)得到。

本文将原始理论方程(4)按2Lb/rf进行展开，使理论方程变得数值稳定，同时保留了原方程的非稳态项，从而得到更高精度的非线性方程，即

为了方便说明，下文中将以上的线性和非线性方程(1)、(2)、(3)和(5)分别简称为LS、LC、NLS和NLC模型。根据KELLY等[23]的理论研究，LS和NLS模型在理论上是一阶精度，LC模型为二阶精度。而本文的NLC方程为四阶精度，理论上比其他3种模型的精度更高，能够得到更准确的层流燃烧速度。

2 实验装置和模型评估方法

本文实验部分在定容燃烧弹上开展，实验装置的具体描述见文献[24-26]，图1所示为其示意图。本实验系统主要是由定容燃烧弹腔体、高速纹影摄像系统、配气系统、点火系统以及温度压力监控系统组成。定容燃烧弹腔体是一个长为210 mm、内径为180 mm、体积为5.58 L的不锈钢圆柱体，两端各装有一片光学直径为80 mm的石英玻璃窗口以便形成光路。燃烧弹腔体外表面缠绕的加热带用于预热可燃混合气。腔内混合气温度由安装在腔体内部的K型热电偶进行实时监控。在容弹腔体中心线处水平径向布置一对电极用于点燃混合气。混合气由高纯燃料、氧气和氮气组成，并依据分压原理通过压力变送器定量混合气比例。经过10 min左右的等待，腔体内混合气混合均匀。开启点火-高速摄像同步系统，相机以10 kHz的拍摄速度记录火焰的传播历程。

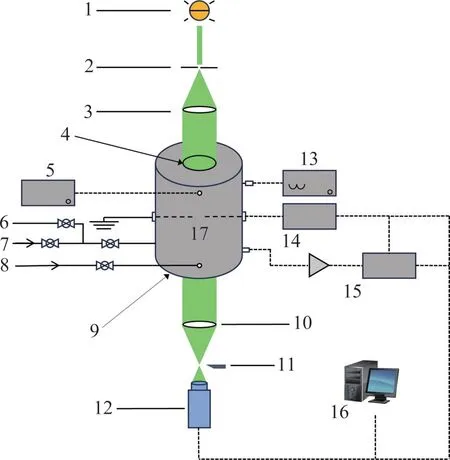
图1 实验装置示意图Fig.1 Schematic of experimental setup

本文实验是在常压下开展的，其中甲烷/空气混合气初始温度为353 K，当量比(ϕ)范围为0.6～1.4，采用较高的初始温度是为了获得更宽广当量比范围内稳定的火焰，且不受浮力不稳定性的影响；正丁烷/空气混合气初始温度为303 K，当量比为0.8；氢气/空气混合气初始温度为303 K，当量比为5.0。

本文模拟采用Chemkin-Pro软件中一维自由传播火焰计算层流燃烧速度。计算采用的化学反应动力学机理为GRI Mech 3.0[27]，Aramco Mech 2.0[28-29]和USC Mech 2.0[30]。模拟过程中考虑了Soret扩散和多组分输运的影响。

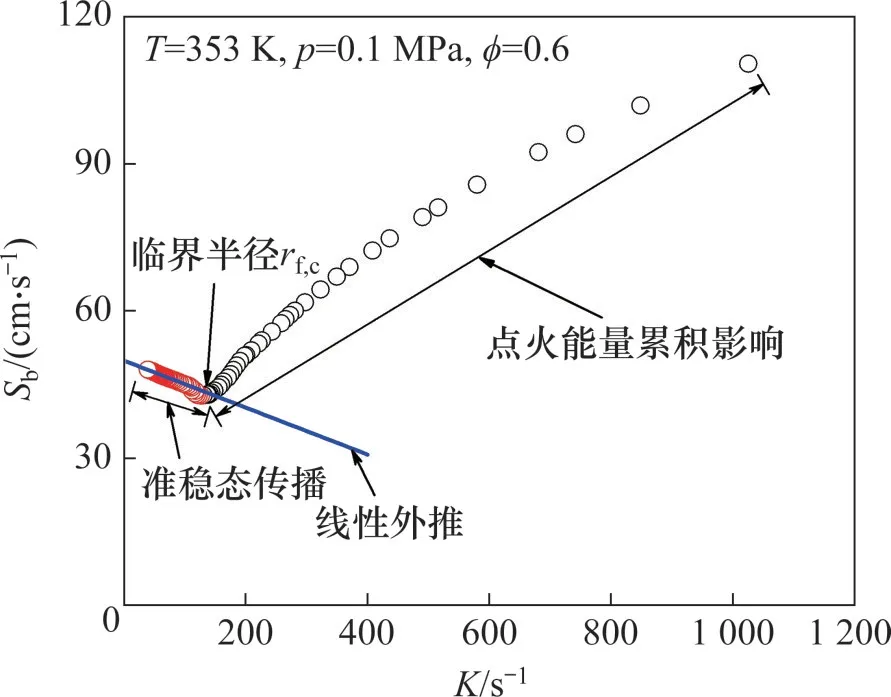
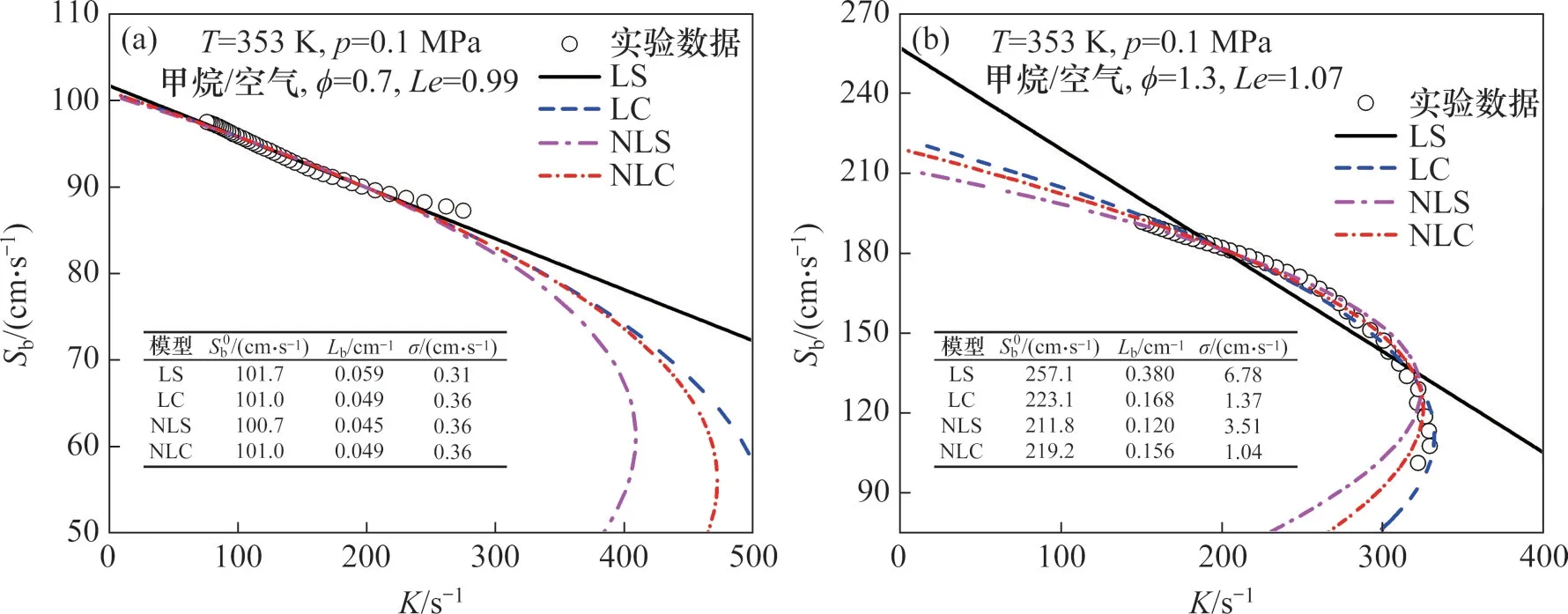
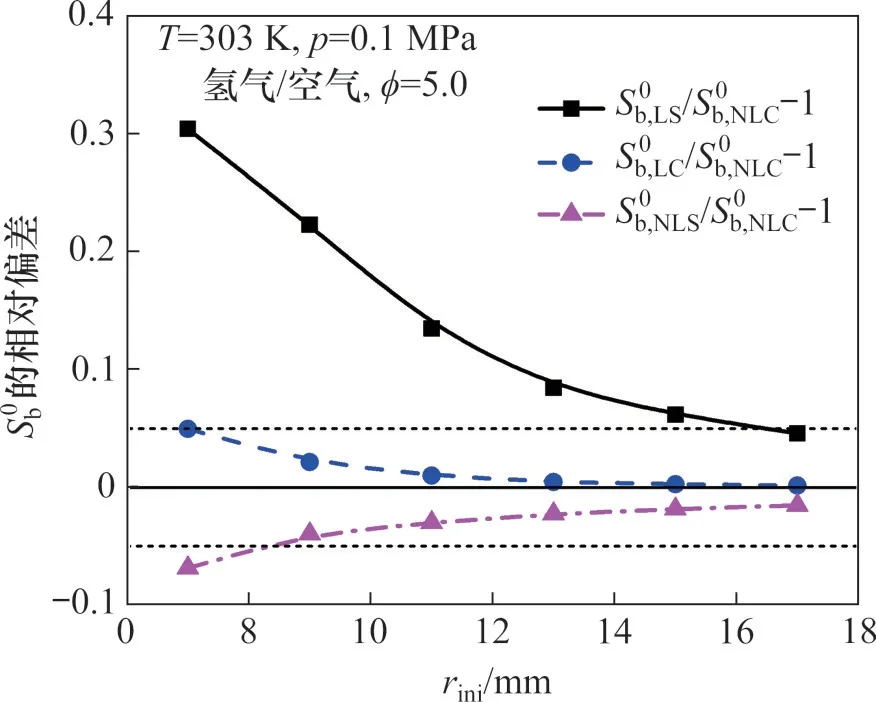
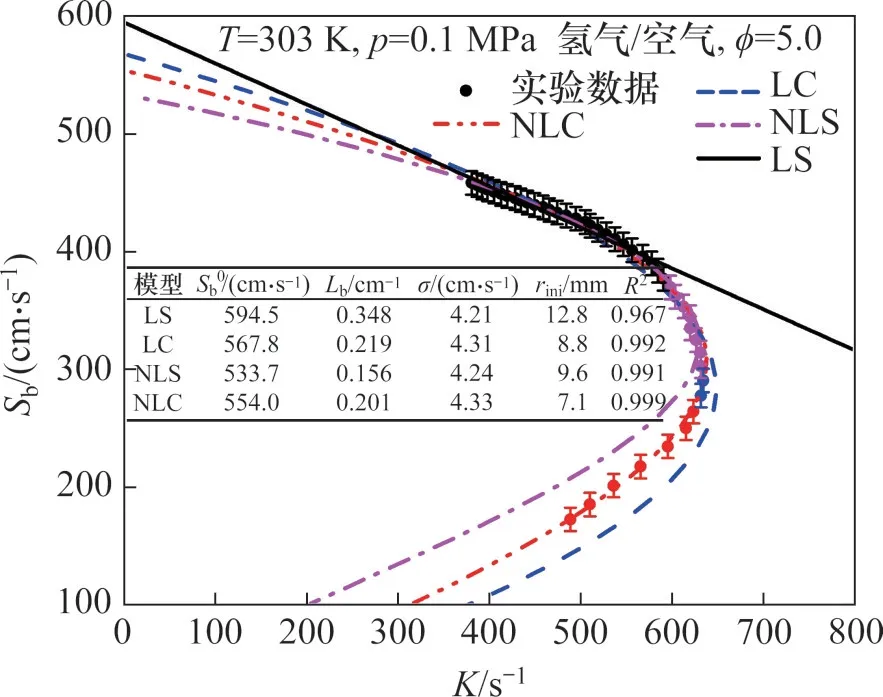
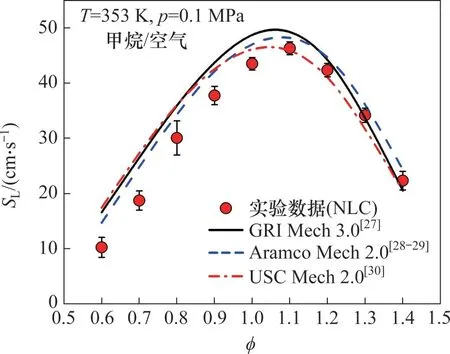
本文基于实验火焰传播速度与外推方程的偏差，采用实验测量数据对不同外推方程的性能进行定量评估。具体对于实验测量获得的Sb-K曲线中的部分数据rf,i1

其中：N为被处理数据点的数目；Sb,exp(i)和Sb,cal(i)分别为实验测量和方程计算的火焰传播速度。对于同一火焰相同的半径范围，采用不同方程处理将得到不同的σ(i1,i2)。数值越小则表明该方程能更加准确地描述实验数据并获得更加准确的层流燃烧速度，即方程的实际精度越高；相反，数值越大，则表明方程的实际精度越低。另外，σ(i1,i2)强烈依赖半径范围的选取，因此，可以采用σ(i1,i2)的变化来确定合适的半径范围。假设rf,i1或者rf,i2受到点火、火焰不稳定性或者腔体的影响时，任何外推方程都无法处理这些半径。并且此假设是合理的，因为外推方程本身无法描述点火、不稳定性和腔体的影响。因此，可以通过σ(i1,i2)的变化确定不受影响的半径范围rini,c=rf,i1c

3 结果和讨论

3.1 点火对半径选取的影响

实验测量层流燃烧速度的半径范围主要受点火、火焰不稳定性和腔体的影响。确定不受点火影响的半径范围十分重要。燃烧过程开始于初期的点火能量积累，当电极放电点火后，会迅速形成快速向外传播的冲击波，后面紧跟速度较慢的热波[31]。最初火焰传播速度极快，随后迅速降低，最终达到准稳态传播。本文选取ϕ=0.6的甲烷/空气作为研究对象，主要是该火焰的马克斯坦长度非常接近零，火焰传播速度几乎与拉伸率呈线性关系。图2所示为稀甲烷/空气(ϕ=0.6)的火焰传播速度Sb随拉伸率K的变化。从图2可知：在火焰向外传播的过程中，点火对火焰的影响逐渐减小，直到达到临界火焰半径(rf,c)后点火的影响基本消失，该火焰的临界火焰半径rf,c=6.7 mm，这与BRADLEY等[31]建议的6 mm很接近。

图2 确定点火影响的临界半径Fig.2 Determination of critical radius of ignition effect

此外，本文中研究的甲烷/空气、正丁烷/空气和氢气/空气在常压下进行，所有火焰为正马克斯坦长度，火焰在实验视窗范围内不会出现胞状结构，即火焰不受质热扩散不稳定性和流体动力学不稳定性的影响。BURKE等[7]研究发现：当rf<0.3rw时，腔体的影响可以忽略不计，其中rw为容弹内腔半径。因此，本实验装置中小于27 mm的火焰将不受腔体影响。本文选取7～24 mm火焰半径测量层流燃烧速度，以消除点火和腔体的影响。

3.2 非线性拉伸对速度提取的影响

本文主要研究正马克斯坦长度条件下，非线性拉伸对层流燃烧速度测量的影响，CHEN[17]采用模拟方法研究了LS、LC和NLS这3种速度外推方程，发现路易斯数Le对速度提取影响较大，故本文选取2类Le(Le接近1和远大于1的情况)的4种具有正马克斯坦长度的火焰进行研究。1) 稀甲烷/空气(ϕ=0.7)火焰，Le约等于1，该火焰具有很小的马克斯坦长度，并受较弱拉伸影响；2) 浓甲烷/空气(ϕ=1.3)火焰，Le略大于1，该火焰具有较大的马克斯坦长度，并受较弱拉伸影响；3) 稀正丁烷/空气(ϕ=0.8)火焰，Le大于1，与甲烷性质相反的典型碳氢燃料，该火焰具有较大的马克斯坦长度，并受较弱拉伸影响；4) 浓氢气/空气(ϕ=5.0)火焰，Le大于1，该火焰具有很大的马克斯坦长度，并受较强拉伸影响。

常压下稀甲烷/空气(如ϕ=0.7)混合气火焰传播速度与拉伸率基本呈线性关系，但随着当量比的增加，火焰传播速度随拉伸率变化的线性关系逐渐变弱，当混合气较浓时(如ϕ=1.3)，火焰传播速度与拉伸率呈明显的非线性关系[11]。图3所示为2种较稀和较浓甲烷/空气混合气火焰传播速度随拉伸率的变化关系。图3(a)中，Le为0.99，火焰传播速度与拉伸率呈明显的线性关系，用4种处理方法提取的无拉伸火焰传播速度和马克斯坦长度很接近。4种处理方法与实验数据的拟合程度均很好，火焰传播速度的偏差(σ)为0.31～0.36 cm/s。同时4种模型获取S0b和Lb的最大相对偏差分别为1.0%和30.0%，说明对于该火焰4种模型提取层流燃烧速度均足够精确，当然马克斯坦长度的差异仍然较大。图3(b)中，Le为1.07，但与稀甲烷/空气火焰不同，火焰传播速度与拉伸率呈明显的非线性变化关系。对于火焰传播速度的偏差(σ)，线性LS模型的σ为6.78 cm/s，大于其他3种非线性模型的σ(1.04～3.51 cm/s)。导致4种模型得到的无拉伸火焰传播速度和马克斯坦长度有明显的差异，并且线性LS模型得到的结果明显大于其他3种非线性模型得到的结果。这4种模型获取S0b和Lb的最大相对偏差高达21.4%和215.7%，说明对于该火焰用线性模型提取层流燃烧速度已不准确，一定程度上可解释文献中浓甲烷/空气实验测量SL数值比较分散。另外3种非线性模型LC、NLS和NLC模型获取的S0b和Lb的最大相对偏差为5.4%和37.3%，表明3种非线性模型的差异较小，即对于该火焰用不同非线性模型提取层流燃烧速度均满足精度要求。从图3可以发现：拉伸率逐渐减小，非线性拉伸率对火焰传播速度的影响逐渐减小。因此，在实验条件允许的情况下，选取较大的初始火焰半径可减小线性处理方法的误差，但LS模型的系统误差无法消除。在火焰发展后期，LC模型得到的结果稍微偏离实验数据点，而NLS和NLC模型得到的结果则基本与实验值一致，并且更有希望准确预测火焰后期发展。因此，对于该火焰NLS和NLC模型要优于LC模型。

图3 路易斯数Le接近1的2种典型火焰Fig.3 Two typical flames with near-unity Lewis number Le

在大Le(或大Lb)下，例如浓氢气/空气，火焰传播速度与拉伸率呈显著的非线性关系，非线性拉伸将强烈影响层流燃烧速度的测量。图4所示为稀正丁烷/空气(ϕ=0.8)火焰和浓氢气/空气(ϕ=5.0)火焰传播速度与拉伸率的变化关系。图4(a)所示的稀正丁烷/空气火焰具有较大的Lb，主要是由较大的Le导致。虽然火焰受到的拉伸较弱，但火焰发展前期，拉伸对火焰传播速度的影响仍然很大，火焰传播速度随拉伸率成明显的非线性关系。对于拟合得到火焰传播速度的偏差(σ)，LS模型为9.92 cm/s，高于NLS模型的6.04 cm/s，明显高于LC模型的1.39 cm/s和NLC模型的0.50 cm/s。也就是说NLC模型表现最好，LC模型比NLS模型和LS模型好，LS模型表现很差。同时用4种模型获得的结果差异很大，S0b和Lb的最大相对偏差分别达到34.4%和316.4%。线性LS模型将明显高估层流燃烧速度，其他3种非线性模型中，在火焰发展后期LC和NLS模型分别稍稍高估和低估火焰传播速度，这样也会导致最终稍稍高估和低估Sb0。相比之下，NLC模型除了在火焰发展前期与实验值吻合很好外，火焰发展后期仍然与实验值保持一致，因此能更好地预测火焰的发展，即能获取更准确的层流燃烧速度。3种非线性模型提取S0b和Lb的最大相对偏差分别为8.4%和65.0%，即3种非线性模型的结果仍然存在较大差异，所以选取高精度的非线性模型很有必要。图4(b)所示的浓氢气/空气火焰具有很大的Lb，主要是由于很大的Le和氢气强烈的优先扩散共同导致的。火焰传播过程中受强烈的正拉伸影响，将强烈抑制火焰的传播，并且火焰传播速度随拉伸率存在强烈的非线性依赖关系。因此，该火焰层流燃烧速度的提取将受到很强的非线性拉伸影响。线性LS模型和非线性NLS模型的火焰传播速度的偏差(σ)高达55.88 cm/s和22.24 cm/s，明显高于非线性LC模型的7.90 m/s，且远高于NLC模型的2.90 cm/s，即NLC模型的精度明显高于LS和NLS模型的精度，并且相比于LC模型，NLC模型的精度也有明显提升。说明NLC模型对于大Le或大Lb火焰，具有最高的精度。从图4可见线性方法很大程度上高估了S0b和Lb，4种方法提取的S0b和Lb最大相对偏差高达40.0%和366.7%，远远超出误差允许的范围。因为线性LS模型无法处理前期受到强烈非线性拉伸的实验数据。3种非线性模型提取的结果也有很大的差异，S0b和Lb最大相对偏差分别为12.7%和65%。对于此类大Le或大Lb火焰，需采用非线性NLC模型，才能获得准确的层流燃烧速度。

图4 路易斯数Le大于1的2种典型火焰Fig.4 Two typical flames with super-unity Lewis number Le

综合这4种正马克斯坦长度火焰，在Lb接近0时(如稀甲烷/空气(ϕ=0.7)火焰)，非线性拉伸的影响非常小，4种模型得到的结果很接近；在Lb较大时(如浓甲烷/空气(ϕ=1.3)和稀正丁烷/空气(ϕ=0.8)火焰)，线性LS模型明显高估S0b和Lb，而其他3种非线性模型(LC、NLS和NLC模型)差异较小；在Lb很大时(如浓氢气/空气(ϕ=5.0)火焰)，线性LS模型远远高估实验值，另外3种模型差异也较大，其中NLC模型能相对更好地预测实验值。总之，随着Lb的增加，非线性拉伸对层流燃烧速度的提取影响将变大，不同模型处理的结果的差异也变大，其中本文提出的NLC模型始终能更准确地描述火焰的传播历程，并能获取更准确的S0b和Lb。

3.3 降低非线性拉伸影响的方法

从球形火焰发展历程来看，火焰发展早期火焰受很强的拉伸，并且拉伸的影响成明显具有非线性，随着火焰向外传播，拉伸率逐渐变弱，并且拉伸的影响逐渐趋于线性[11]。所以在用于测量实验点足够的前提下，增加速度提取的初始半径，将有效抑制非线性拉伸对速度提取的影响。本文以NLC模型为基准，研究不同初始半径对浓氢气/空气(ϕ=5.0)火焰的影响。图5所示为不同初始半径条件下LS、LC和NLS模型相对于NLC模型获取S0b的相对偏差。由图5可知：随初始半径的增加，不同模型提取S0b的差异变小，当初始半径rini=17 mm时，线性LS模型提取的S0b也达到较高精度(与NLC模型差异在5%以内)。可见，适当增加初始半径可以减小非线性拉伸对速度提取的影响，甚至在较大的初始半径条件下，线性LS模型也能得到较精确的测量结果。但值得注意的是通常用于提取速度的实验点不能少于25个，同时受不稳定性和腔体的影响[5]，终止半径会受到实验装置和研究工况的限制。初始半径选择过大将可能导致可用的数据点小于需求的最小值。对于非线性LC和NLS模型，适当增加初始半径即可提取出高精度的层流燃烧速度。综合来讲，采用精确的非线性模型，并适当加大初始火焰半径是降低非线性拉伸对层流燃烧速度测量影响的有效手段。

图5 不同初始半径对层流燃烧速度提取的影响Fig.5 Effect of different initial flame radii on extraction of laminar burning velocity

图6所示为在固定终止半径rend=24 mm，采用不同外推方程和对应合适初始半径rini条件下提取层流燃烧速度的结果。其中，火焰传播速度的偏差σ保持在(4.3±0.15) cm/s，即4种外推方程在合适的半径范围内均与实验测量值吻合很好。不难发现线性LS模型能处理的半径范围最窄(rini=12.8 mm)，接下来是非线性NLS和LC模型(rini=9.6 mm和8.8 mm)，而本文提出的NLC模型适用的半径范围最宽(rini=7.1 mm)。主要原因是火焰发展初期，火焰受强拉伸作用，火焰传播速度与火焰拉伸率成强非线性变化，而本文提出NLC外推方程中的高阶项能很好地描述此非线性依赖关系。或者说，能处理的最小半径主要由外推方程的理论精度决定。而LS、NLS、LC和NLC模型的理论精度逐步由一阶精度提高到四阶精度，因此能处理的最小初始半径逐渐减小，即模型适用的火焰半径范围(拉伸率范围)逐渐拓宽。4种外推方程分别采用合适的半径范围提取的S0b和Lb最大相对偏差为11.4%和123.1%，比原来采用固定半径范围(7～24 mm)的测量的最大相对偏差(40.0%和366.7%)显著减小。并且3种非线性外推方程测量S0b和Lb最大相对偏差为6.4%和40.4%，接近实验测量误差允许范围。

图6 不同模型采用合适的火焰半径提取层流燃烧速度Fig.6 Extraction of laminar burning velocity with suitable initial flame radius for different models

3.4 甲烷/空气层流燃烧速度和马克斯坦长度

图7(a)和7(b)所示分别为采用不同模型提取常压下甲烷/空气在不同当量比情况下的层流燃烧速度和马克斯坦长度，并与化学反应动力学机理GRI Mech 3.0[27]的计算结果进行对比。从图7(a)可知：不同模型测量SL的差异随当量比的增加明显增加，在ϕ=1.4时，SL的最大差异达到7.1 cm/s，远远大于正常的实验误差范围(2～3 cm/s)。从图7(b)可知：不同模型测量结果都表现出Lb随当量比的增加而单调增加，因此，非线性拉伸的影响也随之增加，这将导致不同模型提取SL的差异逐渐增加。当然不同模型测量Lb的差异要更大，特别是在ϕ=1.4时，Lb的最大差异达到0.40 cm。总体来说，为了提高实验测量精度，需要选取精确的非线性外推方程(如NLC模型)，然后适当地增加初始半径进一步减小非线性拉伸的影响，从而获得高精度的层流燃烧速度测量结果。

图7 不同模型提取层流燃烧速度和马克斯坦长度Fig.7 Extraction of laminar combustion velocity and Markstein length using different models

采用球形传播火焰测量层流燃烧速度将受到很多因素的影响，除了本文主要研究的速度外推方程的影响和本文中已经规避的点火、不稳定性以及不稳定性的影响外，还有在较低层流燃烧速度情况下的辐射影响以及最初混合气准备过程中的误差[5]。辐射的影响参考文献[32]进行修正，

其中：SL,RCFS为辐射修正后的层流燃烧速度；SL,Exp为实验测量的层流燃烧速度。S0=1 cm/s，T0=298 K，p0=0.1 MPa。实验整体误差参考CAI等[33]的方法进行评估，

其中：δSL为层流燃烧速度测量的总体误差；BSL为层流燃烧速度测量的系统误差，式(8)中第二项为层流燃烧速度测量的随机误差；M为实验测量重复次数；tM-1,95为自由度为M-1和95%置信区间的t分布值；SSL为层流燃烧速度测量的标准差；xi表示对层流燃烧速度测量影响的因素，ui则是不同影响因素xi导致的固定误差。通过系统的误差分析，得到甲烷/空气火焰层流燃烧速度测量的总体误差为1.2～3.1 cm/s。

图8所示为采用NLC模型测量并通过辐射修正得到的甲烷/空气层流燃烧速度与利用化学反应动力学机理GRI Mech 3.0[27]、Aramco Mech 2.0[28-29]和USC Mech 2.0[30]计算值进行对比。从图8可知：在浓燃和化学计量当量比(ϕ=1.0～1.4)时，机理预测值和实验测量值很接近；而在稀燃条件下(ϕ=0.6～0.9)，机理预测值明显高于实验测量值。在这3个机理中，Aramco Mech 2.0整体上对实验测量层流燃烧速度的预测最准确，主要由于Aramco Mech 2.0在小分子核心机理上进行了一系列优化。

图8 甲烷/空气实验测量层流燃烧速度与不同化学反应机理计算值对比Fig.8 Comparison of methane/air experimental laminar burning velocity and calculated results using different reaction mechanisms