曲线轨道式隔震装置的结构优化与应用研究

2024-03-01赵守江柏文戴君武

中南大学学报（自然科学版） 2024年1期

赵守江，柏文，戴君武

(1.故宫博物院，北京，100009；2.中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨，150080；3.地震灾害防治应急管理部重点实验室，黑龙江哈尔滨，150080)

近现代隔震技术作为结构振动控制的有效方法，目前已广泛应用于工程实践，其性能与效果也在多次地震灾害中得到了检验[1-3]。与此同时，适用于浮放物体的隔震装置在设计研发方面也取得了很大进展[4-5]。尤其是近年来，国内发生的多起强烈地震导致如医疗仪器、通信设备以及馆藏文物等浮放物体的严重损坏[6-8]，从而引发了越来越多的关注与研究。这类隔震装置多为被动式的机械系统，能够利用自身的长周期特性来避开地震能量相对集中的频段，并通过耗能机构抑制位移响应，从而大幅度降低振动的传递。与叠层橡胶支座的剪切变形不同[9]，其水平位移是通过内部起支撑作用的运动副利用自身相对移动来实现。鉴于浮放物体一般体型小、质量轻，运动副的可选型式多样，因此适用的隔震装置种类繁多且各具特点。

在已有的隔震装置中，曲线轨道式是一种结构简单、经济性较强的水平隔震装置[10-11]。它保留了摩擦摆支座的部分特性，具有对地震激励频率范围的低敏感性和高稳定性以及较好的自限位、复位功能，而且整体上更加轻便，构造也更灵活。但目前仍存在一些问题：首先，相比于直线导轨式[12]的嵌入配合，曲线轨道与滚轮之间不能够承受竖向拉力，如何提高装置的整体性是设计的一个重点；其次，由于地震动传播方向的任意性，正交布置的两层轨道需进行水平解耦，故常采用下凹式轨道面或带有轮缘的滚轮来提供侧向力避免脱轨。倘若设计方案不够合理或加工、安装精度不高，滚轮在运动过程中会发生卡滞，影响装置性能的稳定。与此同时，由于构造差异较大，应用于浮放物体的隔震装置在性能评估和试验方法方面还不够完善。例如，现阶段大多仅对装置进行地震模拟试验以测量它在某特定条件下的隔震效率，对其性能参数尤其是阻尼特征的描述较为模糊，对运行的可靠性或稳定性更是缺乏检验。

由于隔震装置原理成熟且相对简单，稳定可靠的构造设计能够有效地促进其推广应用。为此，通过结构优化，设计出一款基于新型抗侧移组件的曲线轨道式隔震装置。该装置既具有整体性强，运行稳定可靠，加工与安装难度低的优势，又可在此基础上进行结构衍变来扩展性能。本文首先介绍它的基本构造和原理，对比理论与试验结果来验证模型的运行质量。然后以雨花阁楼面文物为对象进行具体装置设计，试验研究样机的隔震效果，并探讨建筑滤波效应对该类隔震装置设计的影响，旨在为浮放物体隔震装置的研发和应用提供借鉴。

1 曲线轨道式隔震装置

1.1 基本构造与原理

该类型隔震装置一般由弧形轨道和装有滚轮的滚动框互相配合而成[13]，如图1所示。与直线导轨式不同，滚动框在轨道上的运动轨迹是一条曲线。摆动周期由弧形轨道的曲率半径确定，与上部质量无关。当滚动框在轨道上运动时，重力会产生回复力，阻尼则由滚轮与轮轴接触面间的摩擦或额外设置的耗能机构提供。通过在垂直方向正交叠放两套单向隔震装置即可实现任意水平方向的隔震。

图1 曲线轨道式基本结构示意图Fig.1 Basic structure diagram of curved track type

针对现有隔震装置存在的问题，设计出一套抗侧移组件，如图2所示。该组件包括直线导轨、滑块、导向轴，升降座以及螺母。其中，导向轴的底部法兰与滑块固定连接，上部导轴与升降座的通孔配合；升降座可沿导轴上下移动，且受限于顶端螺母。图3所示为一例加装抗侧移组件的单向水平隔震装置[14]。具体地，直线导轨固定于装有弧形轨道的底板上；升降座与滚动框为固定连接，通过升降座与导轴间的轴向移动来适应滚动框在水平运动过程中的高度变化；导轴顶端的螺母将滚动框与底板连成一整体，防止其脱离。

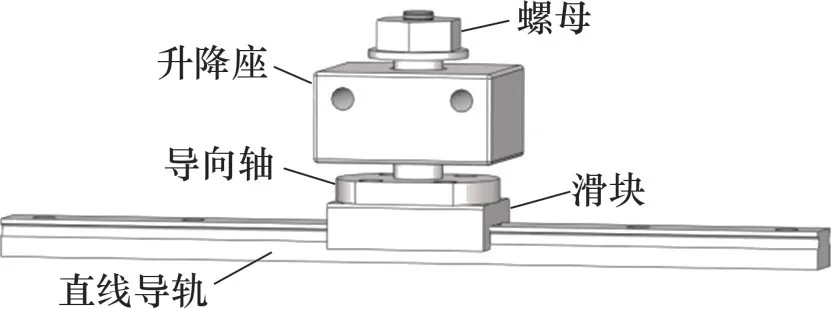
图2 抗侧移组件设计Fig.2 Design of anti-lateral movement component

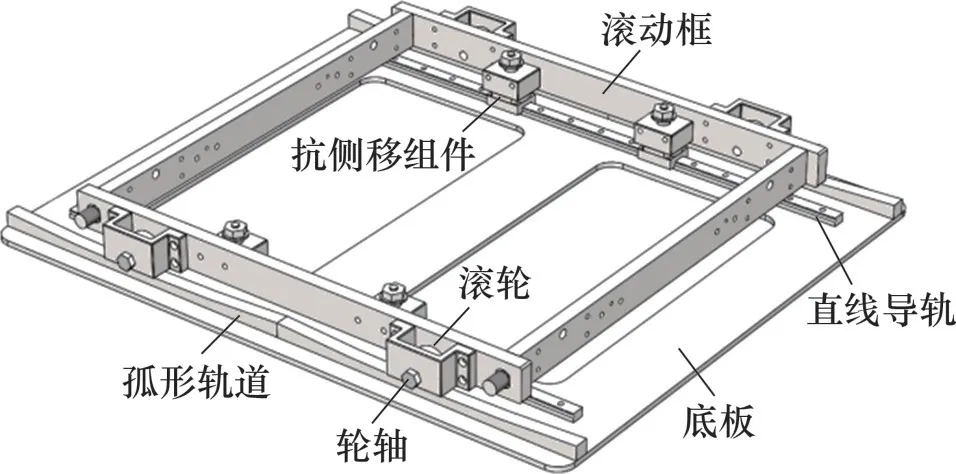
图3 单向曲线轨道式设计Fig.3 Design of unidirectional curved track type

优选的滚动直线导轨副为标准件，技术成熟，价格低廉。由于滑块与直线导轨间为嵌入式配合，滑块可同时承受上下左右方向的负荷及弯矩[15]，所以抗侧移组件既能够为滚动框提供可靠的侧向支撑，又能避免其脱离倾覆，兼具了导向和抗拉功能，提高了隔震装置的稳定性和整体性。而且滚动直线导轨副所产生的附加摩擦力(由自身阻力和侧向力产生)相对极小，对滚动框的运动影响可以忽略；舍弃了轮缘构造的滚轮仅起支撑作用，功能简化，大大降低了装置的加工和组装难度。

通常曲线轨道式可以藉由轮轴间的摩擦耗能，利用两者的直径比或材质来调整阻尼参数。这种耗能方式构造简单，动力特性与上部的质量无关。若为了应对多水准地震作用的考验，提高自适应性，在此基础上装置也可进行结构衍变。例如，抗侧移组件中滑块与升降座之间添加波簧或碟簧，使滑块也能分担一定的荷载。由于滚动直线导轨副的摩擦因数极小，因此，拉低了装置初始的整体摩擦因数，更易于装置启动；随着升降座在水平移动过程中高度的增加，滑块分担的荷载减少，整体摩擦因数增大，有利于抑制位移响应。另外，滚轮也可直接采用滚动轴承，通过增设独立的阻尼机构来辅助耗能。

1.2 运动方程

除不用考虑水平向耦合效应外，曲线轨道式隔震装置(不包括衍生型)与传统摩擦摆的力学模型基本一致。根据已有的研究成果[16]，曲线轨道式的力学模型可为线弹性弹簧与摩擦阻尼器的结合。在水平地震动激励下，其运动方程为

式中：m为滚轮所支撑的质量；u为相对位移；R为轨道的曲率半径；mg/R为隔震装置的刚度；sgn(∙)为符号函数；为地震动加速度；Fd为隔震装置的综合摩擦力，具体为

式中：μ为滚轮的摩擦因数；f为抗侧移组件的摩擦阻力。一般而言，滚动直线导轨副的摩擦因数约为0.004，在采取措施降低滑块的预压力和刮油片阻力后，抗侧移组件的摩擦阻力f相对较小可忽略不计。此时装置的响应加速度a简化为

2 装置性能试验

根据式(1)和式(2)可知，曲线轨道式的动力特性与上部质量无关，理论上通过调整轨道曲率半径和摩擦因数即可改变隔震装置的刚度和阻尼特性，满足特定的隔震需求。因此，针对上述设计方案的性能试验，其目的更侧重于检测试验装置的运行质量，验证各零部件尤其是抗侧移组件能否发挥预期功能。

2.1 模型与方法

鉴于方案模型的性能检验不受外形尺寸的影响，本着便于安装和节约材料的原则，设计制作了一款单向水平隔震试验模型，如图4所示。其弧形轨道为不锈钢材质，宽度为8 mm，曲率半径为2 m，摆动周期为2.84 s，极限位移为±100 mm。滚轮外径为19 mm，外圈为不锈钢材质，内嵌石墨铜套。轮轴为不锈钢材质(未抛光)，直径为6 mm。抗侧移组件中滚动直线导轨副为MGN9C型滑块及配套导轨，每根导轨上配2个滑块。模型底板为铝材，中部设置限位块。滚动框以及载物架也均为铝材。滚轮所支撑的总质量为5.1 kg。

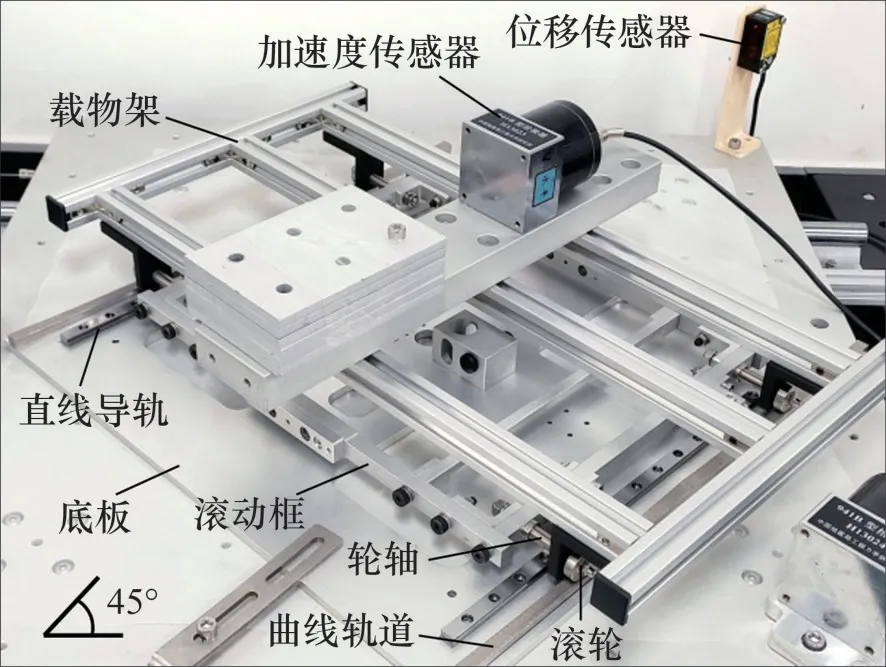
图4 试验模型及布置Fig.4 Test model and setup

试验采用一套单向水平地震模拟振动台。台面长×宽为0.6 m×0.6 m，行程为±150 mm，最高速度为0.85 m/s。选用松下HG-C1400型激光位移传感器进行位移测量，测量中心距离和测量范围为(400±200) mm，精度分别为300 μm(测距200～400 mm)和800 μm(测距400～600 mm)。加速度传感器为941B型低频拾振器，灵敏度为0.3 V·s2/m。其他辅助试验设备还包括微型S型拉力传感器及变送器等。

试验前先测量滚轮在2条平直轨道上运动时的摩擦因数；然后将试验模型的底板固定于振动台面上，轨道方向与振动台运动方向成45°角；配重固定于载物架顶部；振动台和试验模型分别布置一个加速度传感器，与模型轨道方向保持一致。试验除采用振幅为5 cm，频率为1 Hz的正弦波激励外，还进一步利用地震波输入来检验模型的运行情况，得到响应时程曲线，并与理论分析结果进行对比。所选地震波为1994年Northridge地震CDMG24278台站的090分量，峰值加速度为0.568g。

2.2 结果分析

图5所示为正弦波作用下试验和理论分析所得模型的相对位移时程曲线。其中，对试验进行数值模拟时，采用实测的振动台面加速度作为输入激励，并假定动静摩擦因数一致。经测量，当滚轮支撑的总质量为5.1 kg、移动速度为20 mm/s时，滚轮摩擦因数约为0.06。

图5 正弦波作用下模型的相对位移时程曲线对比Fig.5 Comparison of relative displacement time-history curves of model under sine wave

由图5可知：试验模型初时保持静止，在激励输入后能够快速地进入稳态振动。稳态反应下的位移响应曲线光滑且无毛刺和突变，频率与振幅基本保持恒定。理论分析与试验所得时程曲线吻合良好，进一步验证了装置运行的可靠性与准确性。

图6所示为试验模型在Northridge地震波作用下的振动响应结果。由于地震波的特性更加复杂，单纯试验虽可评估模型的隔震性能，但无法判断其运行状况，因此必须借助理论计算对比分析，通过结果的吻合程度验证试验模型的运行质量以及数值模型的准确度。此处采用曲线拟合优度指标RNL来衡量图中曲线的吻合程度[17]，其计算公式如下：

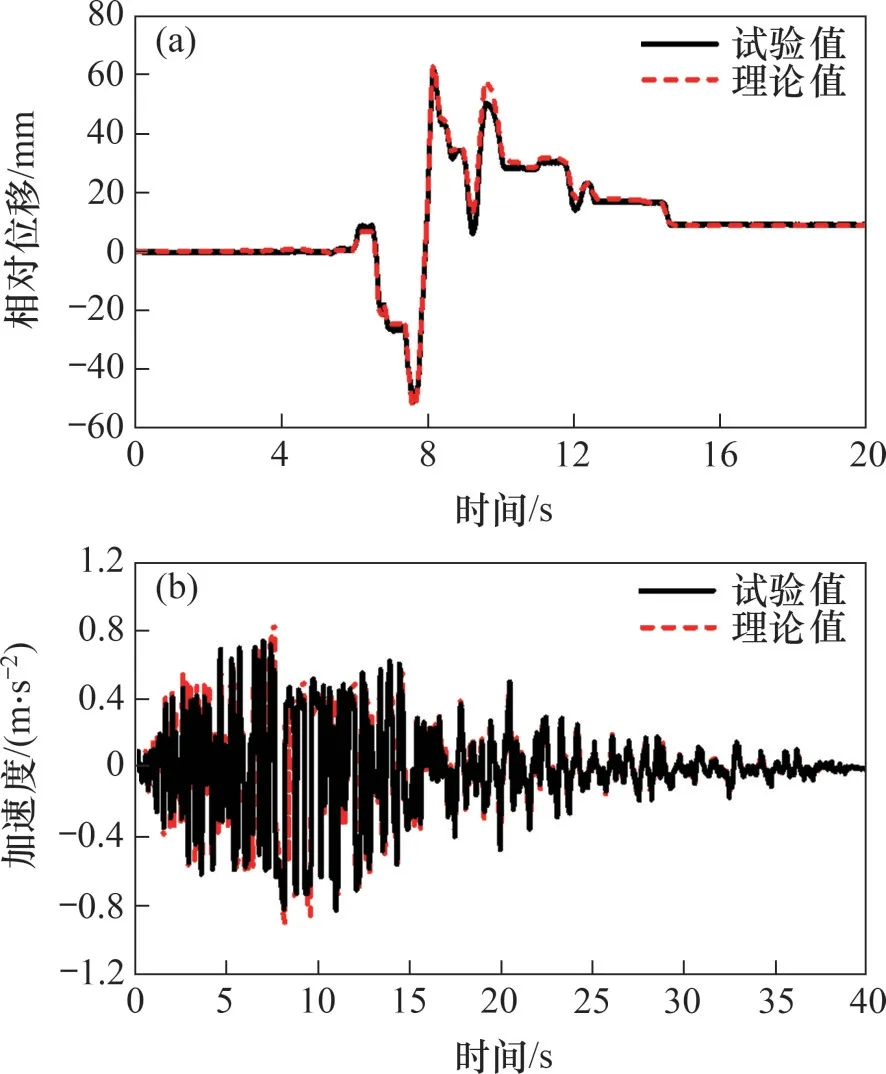
图6 地震波作用下模型的动态响应时程曲线对比Fig.6 Comparison of dynamic response time-history curves of model under seismic wave

式中：为试验数据；yi为理论数据。RNL愈接近于1，表示两者的吻合性愈好。该指标将残差平方和与相对误差有机结合在一起，几何意义清晰且计算简单。截取试验模型响应较剧烈的6～15 s时间段进行分析，并与峰值比ρpeak比较，如表1所示。

表1 吻合度指标RNL与ρpeakTable 1 Indices of agreement RNL and ρpeak

由表1可知：采用地震波输入时，理论分析与试验数据虽略有差别但整体上较为吻合，其中相对位移吻合程度要优于加速度吻合程度。相较于单一的峰值比，采用时程曲线对比显然更能全面表现理论与试验的吻合程度。从图6可以看出：试验与分析所得曲线不仅在趋势上大致相符，而且各峰值吻合度较高。以上结果表明：即便在复杂激励下，试验模型中的抗侧移组件依然能够提供可靠的侧向支撑且未产生负面作用；隔震装置设计方案合理，质量稳定可靠。

需要说明的是，试验中振动台输入激励与模型的运动轨道成45°夹角，因此它的一个激励分量与模型水平运动方向相同，促其运动，另一分量与运动方向垂直，使之产生侧向惯性力。而上述理论分析均未考虑式(2)中抗侧移组件的摩擦阻力f，即忽略了侧向惯性力所产生的影响。试验与理论结果对比差异不明显，因此，抗侧移组件充分发挥了解耦作用，在分析中仅需考虑运动方向上的激励即可。若正交叠放两层单向隔震装置形成一套完整的水平隔震系统，忽略两层间的耦合效应是切实可行的。

3 应用研究

以故宫雨花阁整体防震保护为背景，参考文献[18]中相关研究，尝试对楼内器物进行隔震装置设计与试验研究。由于地震波经建筑的滤波和放大后，在各层楼面会形成新的绝对加速度时程曲线，简称楼面波，因此选取最不利的顶层楼面进行分析，将楼面波作为输入波。其中，浮放文物和隔震装置的质量与建筑自身相比均可忽略不计，因此，无需与建筑结构组成复合体系进行动力分析。

3.1 双层同向曲线轨道式设计

为兼顾陈列文物的展示效果，隔震装置体积不易过大，因此，弧形轨道的长度受到了限制。借鉴双凹摩擦摆的构造特点[19]，在同一轮轴上设置内外滚轮，分别对应上下层弧形轨道，形成了双层同向曲线轨道式构造，如图7所示。在相同平面尺寸的前提下，该构造能够获得更大的位移容量和更低的装置高度。经受力分析可知，若忽略自重，除轮轴外，滚动框承受的剪力为零；同轴的两滚轮间距小，框架所受的弯矩也很低。因此该构造能够极大地缩减构件截面尺寸，并降低框架的加工与装配难度。

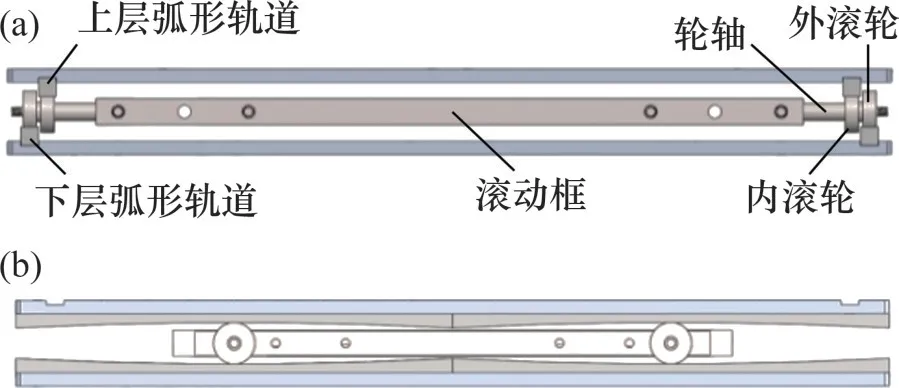
图7 双层同向曲线轨道式设计Fig.7 Design of double-layer codirectional curved track type

依据该构造，在图4所示方案模型的基础上，组装出一套完整的曲线轨道式隔震装置样机(未含外罩)，如图8所示。它是由2套双层同向曲线轨道式正交叠放而成。其长×宽×高为400 mm×400 mm×71 mm，质量为4.1 kg，极限位移为±200 mm。零部件的材质、规格或加工质量等均与方案模型保持一致。由式(3)可知：在极限位移范围内，样机的加速度响应峰值不超过0.16g。

图8 隔震装置样机Fig.8 Prototype of isolation device

3.2 振动台试验

根据文献[18]可知，雨花阁南北向一阶固有频率为1.45 Hz。当分别输入峰值加速度(PGA)为0.2g的El Centro波、Taft波和Ninghe波后，顶层楼面波的峰值加速度分别扩大到0.54g、0.67g和0.41g，其频谱特征也发生较大改变。图9所示为顶层楼面波与相应地面输入波的傅里叶谱对比。

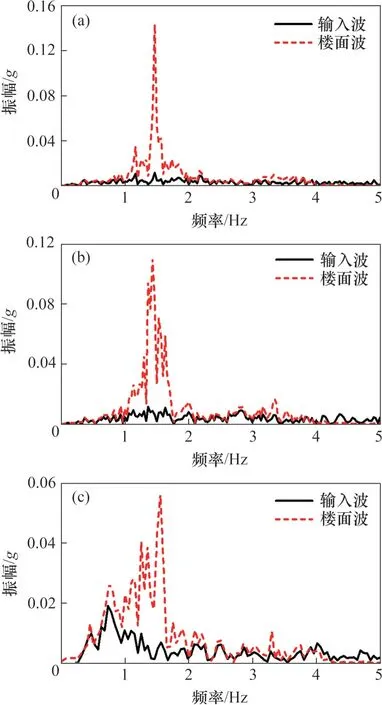
图9 输入波和顶层楼面波的傅里叶谱图Fig.9 Fourier spectra of input and top floor waves

由图9可知：雨花阁本体结构不仅能够增强与自身频率相近区段的振动能量，还起到了类似低通滤波的效果，即它可通过并轻微放大输入波低频段的振动能量，同时削弱其高频成分。楼面波因此既反映了建筑结构的性质，又夹带着地震激励特性。

隔震装置样机固定于振动台面，底层轨道与振动台的运动方向保持一致。样机顶板总质量为2.2 kg。试验时分别输入3条顶层楼面波，结果如表2所示。由表2可知：在El Centro和Taft楼面波作用下，隔震装置的位移响应均在允许范围内，减震效率分别为77%和82%。但在Ninghe楼面波作用下，装置的位移响应将超出极限位移，滚动框与限位块发生了碰撞，加速度响应峰值极大，后期应用时须采取措施如增加装置的阻尼耗能或轨道长度。上述现象的原因主要是隔震装置的响应对输入波中的低频成分更敏感。虽然El Centro波和Taft波的卓越频率与建筑频率接近，它们楼面波的加速度增幅较大，但Ninghe波的低频成分更丰富，对隔震装置的振动影响更显著。

表2 楼面波作用下样机的峰值响应Table 2 Peak response of prototype under floor waves

同时还发现，相同条件下对样机进行多次测试，其振动响应结果存在些许差异。这里仅列出样机顶板和滚动框在El Centro楼面波作用的振动响应结果，如图10和图11所示。由图10可知：在两次El Centro楼面波作用下，样机顶板的加速度响应曲线吻合良好；相对位移响应曲线整体趋势保持一致，多数峰值大体相等，局部差值较大。图11所示的中间滚动框的两次相对位移响应结果却差异显著，在多个相同的时间段内，滚动框或运动或静止，其状态存在不确定性，进而对顶板响应产生些许影响。分析其原因可能为：双层同向曲线轨道式为双自由度体系，非线性动力响应受性能参数和初始状态影响大；且轮轴与滚轮之间实质为滑动摩擦，不仅动、静摩擦因数略有差异，随动性差，还受到加工和装配精度的影响，滚轮与上下轨道间的协同性不够理想。工程中隔震装置若采用多重摩擦摆构造样式，其性能的可靠性与稳定性应予以重视。

图10 El Centro楼面波作用下样机顶板响应时程曲线Fig.10 Dynamic response time-history curves of prototype roof under El Centro floor wave

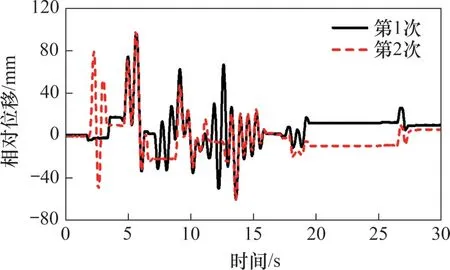
图11 El Centro楼面波作用下滚动框相对位移时程曲线Fig.11 Relative displacement time-history curves of rolling frame under El Centro floor wave

3.3 滤波效应对隔震装置的影响

如前文所述，普通非隔震建筑对地面输入的原始波有放大和滤波效应[20-21]，进而影响到楼面上隔震装置的分析和设计。但是或因体型复杂，或因工作量较大，有时建筑的楼面波难以获取。若借鉴现有的研究成果[22-23]，根据楼面加速度放大系数，直接采用调幅后的原始波作为装置设计条件显然更加便捷。因此，为研究滤波效应的影响，针对式(1)所示的单自由度曲线轨道式隔震体系，摆动周期摩擦因数取0.06，不考虑其他附加摩擦力，采用上述3条楼面波以及调幅后的原始地震波进行反应谱分析，结果如图12所示。

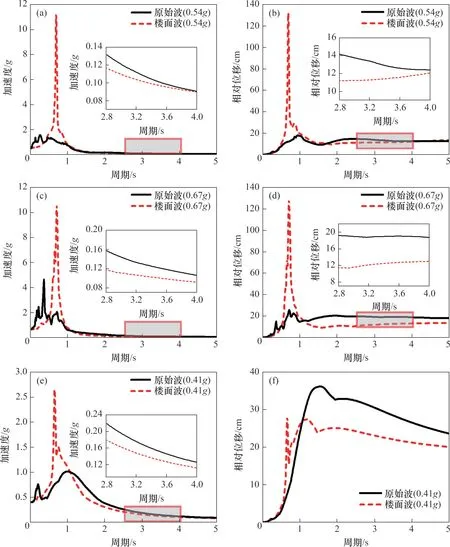
图12 相同峰值加速度的原始波和楼面波作用下曲线轨道式的反应谱Fig.12 Response spectra of curved track type under original and floor waves with the same peak acceleration

由图12可知：在周期0～1 s段，原始波和楼面波所引起的隔震装置加速度反应谱以及位移反应谱均差异明显，尤其是在摆动周期与楼面波的卓越周期(0.69 s)相近时，装置的振动响应十分剧烈。随着隔震装置周期增大，在原始波或楼面波作用下其反应谱曲线逐渐平缓。周期1～2 s段大致属于过渡段，无论是加速度反应谱还是位移反应谱，波动开始趋于稳定。在周期2～4 s区段，谱曲线的波形单调且变化幅度更小，其中隔震装置在原始波作用下的振动响应均大于在楼面波作用下的响应，且两者的差距随周期增大而逐渐缩小甚至曲线发生重合。鉴于隔震装置的周期大多位于该区段，远离建筑的自振周期，因此，在建筑楼面波不易获取的情况下，作为一种简化方法，选用调幅后的原始波进行隔震装置设计是可行的且偏于安全。