三向非等压应力场下围岩主应力差与塑性区分布关系研究

2024-03-01刘洪涛韩子俊韩洲陈子晗韦晟杰刘勤裕程文聪吴双

中南大学学报（自然科学版） 2024年1期

刘洪涛，韩子俊，韩洲，陈子晗，韦晟杰，刘勤裕，程文聪，吴双

(1.中国矿业大学(北京) 能源与矿业学院，北京，100083；2.煤炭行业巷道支护与灾害防治工程研究中心，北京，100083)

围岩在天然状态下处于弹性变形的三向应力平衡状态，巷道开挖会打破围岩原有的应力平衡状态，周边应力呈动态梯度型分布，导致围岩产生不同程度的破坏[1]。显然，应力矢量的演化规律与巷道围岩的稳定性之间存在密切关系。深入研究巷道开挖后受力状态及应力差异化分布特征、掌握巷道全周期的应力时空演化规律，对探究围岩破坏模式、岩体强度衰减特性、塑性区形态演化规律具有重要的理论价值，同时对探索巷道围岩控制理念与方法、构建围岩协同控制体系以及解决巷道大变形、冒顶、冲击地压等围岩灾害问题具有重要的实用价值[2]。

在巷道围岩应力分布与围岩稳定性关系研究方面，众多学者进行了探究。马念杰等[3-5]以最大主偏应力为指标研究了非静水压力场下偏应力与塑性区分布特征之间的密切关系。赵志强等[6-7]对非等压应力场下圆巷围岩塑性区方程进行重新推导，研究了不同应力比条件下围岩塑性区的扩展特性、形态演化规律，并基于其致灾机理及工程意义提出巷道围岩蝶形破坏理论。尹光志等[8-11]基于不同强度准则研究了考虑中间主应力作用的围岩变形及塑性区半径解析解，发现中间主应力对围岩强度有重要影响。

大量的岩石力学试验结果表明，在围压较低时岩体的破坏整体上由张拉破裂控制，随着围压的增加，剪切裂纹数开始增多，岩体破坏开始向剪切破坏转变[12]。由M-C剪切破坏准则可知，围岩主应力差分布与围岩的剪切破坏密切相关，围岩的破坏在很大程度上取决于主应力差值的分布状态。李桂臣等[13]研究了典型断面巷道在高地应力作用下对围岩主应力差分布的影响。何富连等[14-16]以主应力差为衡量指标，对不同工程背景下的巷道围岩主应力差分布特征及变形破坏机理进行了深入分析，并提出了围岩控制新技术。牛双建等[17]基于真三轴模拟实验系统重点分析了松动圈内外主应力差的变化规律，并结合M-C准则及围岩塑性形成过程对主应力差演化机制进行了深入探讨。赵洪宝等[18]基于数值模拟分析了主应力差云图与塑性区之间的对应关系，发现松动圈边界位于最大剪应力的峰值位置。

在对主应力差进行研究时，大多未考虑巷道轴向应力的影响，实际上，巷道开挖后大部分围岩仍处于三向应力状态，忽略巷道轴向应力对围岩强度影响时所得结果与实际结果存在较大差异。因此，本文基于前述研究成果，对三向应力场下主应力差分布规律展开深入分析，并与考虑巷道轴向应力影响的塑性区形态演化规律进行对比分析，探究主应力差分布与塑性区形态分布的关系。基于理论研究，对羊场湾煤矿叠加采动影响下回采巷道的非对称变形异化机制展开分析，并针对性地提出非对称支护联合支护参数，以期为工作面回采以及类似工程条件巷道的稳定控制提供参考。

1 考虑轴向应力的主应力差分布规律研究

1.1 不同应力加载路径下岩体破坏形态分析

在煤矿开采过程中，巷道围岩会经历复杂的围岩应力重新分布过程，应力的重新分布阶段也是煤岩体的加卸荷阶段，围岩所处应力环境的主应力差逐渐升高，不等压性变得更加明显，因此，研究不同应力加载路径、不同应力加载方案下的岩体破坏特征及破坏形式具有重要意义[2]。

本文以宁煤矿区羊场湾煤矿为工程背景，在矿井未受采掘扰动区域进行钻孔取芯，将样品加工为直径为50 mm、高为100 mm的标准试件，对试件进行烘干处理。采用煤、岩2种试件，加载装置采用RTR高温高压岩石三轴仪，应力加载实验包括单轴压缩实验、三轴压缩实验、三轴循环加卸载实验、同步升轴压卸围压实验。不同应力加载条件下的试样破坏形态如图1所示。

图1 不同应力加载条件下试样破坏形态Fig.1 Specimen failure patterns under different stress loading conditions

由图1可以看出，在不同应力加载条件下，岩体破坏分为拉破坏、剪破坏、拉-剪混合破坏3种破坏形式。在单轴压缩状态下，岩体呈拉-剪破坏，但主要以剪破坏为主，局部发生拉伸破坏；在常规三轴压缩状态下，煤岩体呈现明显的剪切滑移破坏；在循环加卸载、升轴压卸围压的状态下，试件基本以剪切滑移破坏为主，部分煤样存在拉伸破坏。

从上述不同应力加载条件下的岩体破坏形式可以看出，试件在围压较小时表现为混合张拉破坏，随着围压比增大，岩体破坏方式逐渐由脆性张拉破坏向单一剪切滑移破坏发展。此外，由摩尔-库仑强度曲线可以看出，围岩的主应力差对围岩的破坏起决定性作用，主应力差的范围在很大程度上决定了围岩的破坏范围。主应力差越大，极限应力圆越容易与包络线相切或处于包络线之外，围岩发生剪切破坏的概率越大。同时，主应力差是一种融合了最大、最小主应力、垂直应力等综合影响作用的应力指标，能更好地反映岩体变形破坏的本质。

1.2 围岩主应力差理论分析研究

目前，井巷、钻孔、硐室、隧道等工程问题研究常常以平面应变模型为基础，简化的平面应变模型在各向均质、同性的水平巷道中适用性较好，而在分析穿层斜井、倾斜巷道及钻孔等工程问题时，平面应变模型忽略了巷道轴向应力的相关应力分量及长轴方向的正剪应变分量[19]。因此，在分析三维问题时应采用全平面应变模型进行分析。全平面应变模型是在平面应变模型的基础上附加一个面外剪切及单轴压缩应力状态而得到的模型。BRADLEY等[20]利用Kirsch解和Fairhurst解推导出极坐标系下孔洞周边任意一点的应力表达式为

式中：σr为任意一点的径向应力；σθ为任意一点的切向应力；σv为巷道轴向主应力；τrθ为任意一点的剪应力；r、θ为巷道周围任意一点的极坐标参数；R为巷道半径；v为围岩泊松比；σz为巷道垂直应力。η1和η2分别为水平侧压比和轴向侧压比，其表达式为

式中：σx为巷道水平应力；σy为巷道轴向应力。

设定：

由弹性力学理论可得极坐标下围岩任意一点的主应力表达式，如式(4)所示。将式(3)代入式(4)可得式(5)：

式中：σ(1)、σ(2)、σ(3)为围岩的三向主应力。在3个方向应力未知的情况下，需要对三向应力进行排序，分为以下3种情况：σ(1)≥σ(3)≥σ(2)、σ(1)≥σ(2)≥σ(3)、σ(2)≥σ(1)≥σ(3)。因而，在探讨主应力差|σ1-σ3|时需要通过排序进行分类讨论。由式(5)可求得不同应力场下主应力差的计算表达式，如式(6)所示。

巷道从开掘到报废一般会经历掘进影响、影响稳定、采动影响、采动影响稳定、二次采动影响这5个阶段[21]，在不同阶段下，围岩围压有时会表现为非常规性，应力增高系数有时高达2～5倍[22]。因此，为研究不同侧压条件下巷道围岩主应力差分布特征，本文选取有实际意义的围压比，通过η1、η2研究不同水平、轴向侧压比情况下的巷道围岩主应力差值演化规律。固定σz=20 MPa，巷道半径为2 m，泊松比为0.2。由于有关水平侧压比条件的研究较多[23]，因此，本文主要讨论轴向侧压比条件下的情况。主应力差计算方案如表1所示。

表1 主应力差计算方案Table 1 Calculation scheme of principal stress difference

将方案Ⅰ、Ⅱ、Ⅲ、Ⅳ的应力代入主应力差表达式，通过数学软件可得到各方案下的巷道围岩主应力差分布形态，如图2所示。从图2可以看出：

图2 不同应力方案下主应力差分布Fig.2 Distribution of principal stress difference under different stress schemes

1) 在轴向侧压比固定、水平侧压比变化的过程中，主应力差分布呈现圆形—椭圆—蝶形的形态演化过程。

2) 在水平侧压比固定、轴向侧压比变化的过程中，当η1=1.0(方案Ⅱ)时，η2变化过程中主应力差分布形态均为圆形；当η1=1.2(方案Ⅲ)时，在不同η2下主应力差分布形态均为椭圆形；当η1=2.0(方案Ⅳ)时，在不同η2下主应力差分布形态均为蝶形。

3) 对方方案Ⅰ、Ⅱ、Ⅲ、Ⅳ可知，主应力差的分布形态主要由η1决定，η2对主应力差的形态分布影响较小。

4) 在弹性解下，主应力差随着距巷道圆心位置距离的增加逐渐减小，在σx、σz较小的一侧应力集中。

2 考虑轴向应力的塑性区边界分布规律

截至目前，三向应力场下巷道围岩的塑性区求解问题一直未能得到有效解决。目前使用较为广泛的塑性区求解思路是基于Kastner求解公式，将弹性理论下的围岩应力分布解直接代入塑性条件下的M-C屈服准则。赵志强等[6]将Kastner公式进行重新整合，基于平面应变问题推导出非均匀应力场下巷道围岩塑性区近似隐式解，并基于一系列塑性区特性研究及工程实践提出巷道蝶形破坏理论。虽然该近似解未考虑岩体的塑性软化特性、岩体残余强度及体积膨胀特性，但对工程实践具有重要的指导意义，因此，该求解方法为考虑巷道轴向应力影响的塑性区求解提供了一定的指导思路。基于第1节分析可知，需要对巷道三向主应力进行排序，因此，基于M-C准则，在三向主应力未知的情况下，可以将Mohr形式转化为

当σ(1)>σ(2)>σ(3)时，(σ(1)-σ(3))=(σ(1)+σ(3))sinφ+2c∙cosφ，有

当σ(1)>σ(3)>σ(2)时，(σ(1)-σ(2))=(σ(1)+σ(2))sinφ+2c∙cosφ，有

当σ(2)>σ(1)>σ(3)时，(σ(2)-σ(3))=(σ(2)+σ(3))sinφ+2c∙cosφ，有

式中：c和φ分别为岩体的内聚力和内摩擦角。式(7)是式(8)、(9)、(10)的集合，即通过式(7)可将巷道周边所有塑性破坏点进行并集处理，从而求得考虑巷道轴向应力影响的围岩塑性区半径。由于该隐式方程求解较为复杂，因此，基于Python编程语言开发塑性区求解软件。该软件操作界面如图3所示。

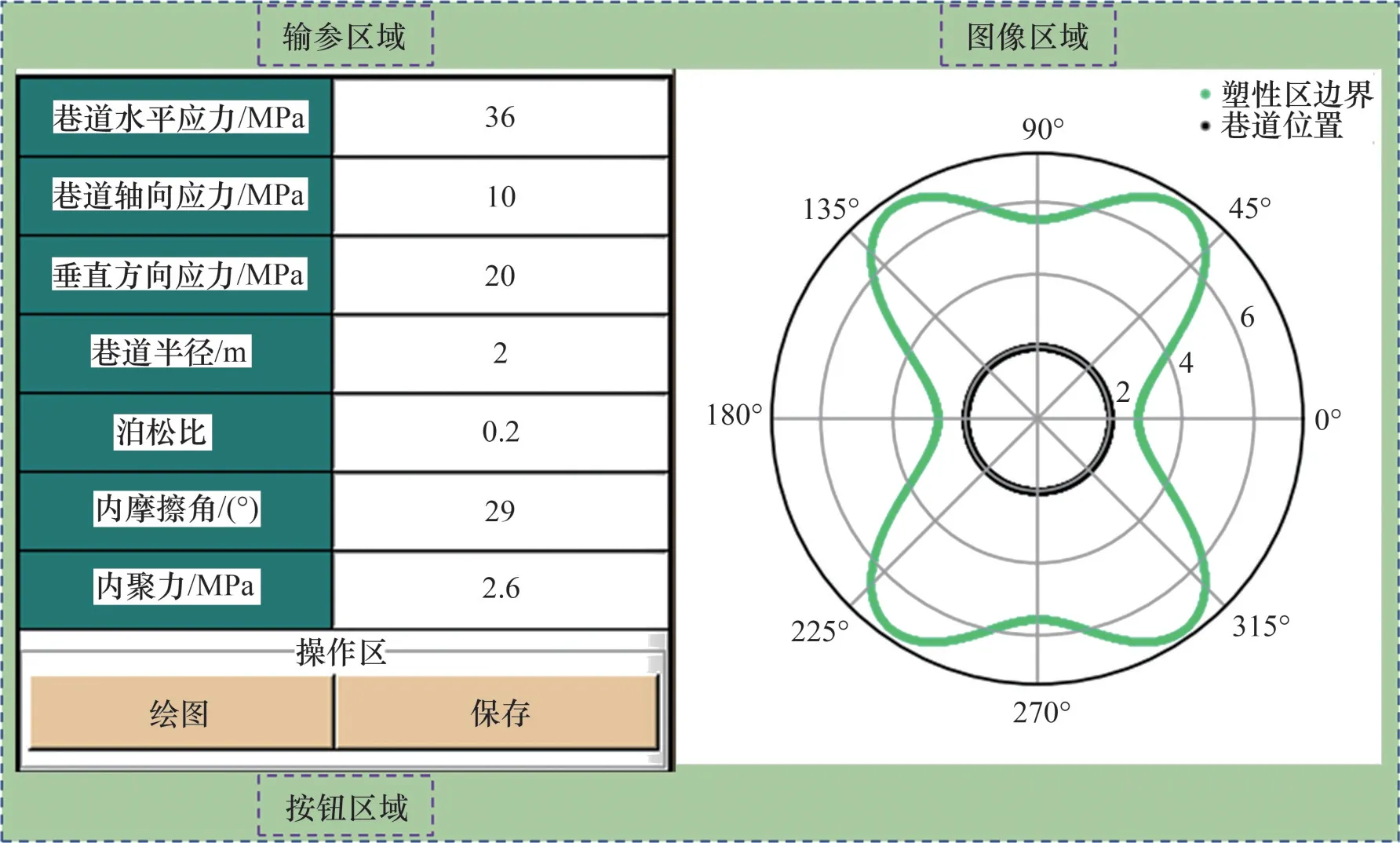
图3 软件操作界面Fig.3 Software operation interface

本文设定内聚力c为2.6 MPa，内摩擦角为29°，将上述方案Ⅰ、Ⅱ、Ⅲ、Ⅳ所对应的应力代入塑性区求解软件，并对所得塑性区图像进行后处理可得到不同应力方案下的塑性区形态，如图4所示。

通过图4形态演化云图可以得出如下规律：

1) 在轴向侧压比固定、水平侧压比变化情况下，巷道围岩塑性区扩展形态会呈现出圆形到椭圆形过渡、椭圆形到蝶形过渡、蝶形恶性扩展阶段共3个阶段。

2) 在水平侧压比固定、轴向侧压比变化的情况下，当η1=1.0时，η2变化过程中围岩塑性区形态均为标准圆形形态；当η1=1.2时，不同η2下围岩塑性区形态均为椭圆形形态；当η1=2.0时，不同η2下围岩塑性区形态均为蝶形形态。

3) 在轴向侧压比η2变化过程中，在某个应力变化区间内，围岩塑性区尺寸不会随着η2的变化而发生变化，当超出一定应力区间后，围岩塑性区尺寸会在原有形态基础上扩展。该规律也说明巷道轴向应力对围岩的稳定性具有重要影响。

4) 结合4种方案塑性区演化特征可知，巷道水平侧压比η1决定围岩的塑性区形态，而轴向侧压比η2对巷道塑性区尺寸影响较大，对形态特征影响较小。

3 围岩主应力差与塑性区分布特征关系

3.1 围岩主应力差与塑性区分布理论结果对比及分析

由上述不同、轴向侧压比情况下主应力差分布规律可以看出，在完全弹性应力条件下，巷道围岩的主应力差分布会呈现不同的形态演化规律。结合塑性区形态演化特征可以看出：1) 在不同的应力加载条件下，围岩主应力差分布及塑性区分布均会呈现出圆、椭圆、蝶形3种形态的演化规律，且在相同应力条件下，二者之间的形态具有一致性，即主应力差分布形态可以在一定程度上反映塑性区的形态变化。2) 在三向应力状态下，的变化对主应力差及塑性区形态变化有重要影响。当为1时，二者分布形态均为圆形，且随着的增大，分布形态由椭圆形逐步过渡到蝶形。轴向侧压比的变化对主应力差及塑性区形态分布影响程度较小，二者分布形态主要由决定。

3.2 数值模拟对比结果及分析

为研究考虑巷道破坏的围岩主应力差分布，采用FLAC3D7.0进行数值模拟分析。模型长×宽×高为80 m×80 m×1 m，网格数量为73 600个，节点数量为111 000个，模型采用M-C本构模型，岩石力学参数与上文理论分析中的参数完全一致，模型应力加载方案见表1。通过编写Fish语言调用围岩主应力差分布云图。在不同应力条件下，塑性区与主应力差分布云图如图5所示。

图5 不同应力方案下主应力差与塑性区对比分析云图Fig.5 Comparative analysis contours of principal stress difference and plastic zone under different stress schemes

从图5可以看出：在为1的情况下，围岩主应力差分布呈圆环放射状分布，巷道同一位置的主应力差完全相同。由于浅部围岩的破碎导致主应力差峰值壳向深部转移，随着的增加，围岩主应力大的区域逐渐形成主应力差卸压壳，主应力小的区域形成主应力差峰值壳。此外，主应力差与塑性区形态均呈现圆形、椭圆形及蝶形变化规律。从图5还可以看出，在相同、轴向侧压比不同情况下，当分别为1.0、1.2、2.0时，主应力差图谱分别呈现圆形、椭圆形及蝶形的分布形态，与塑性区形态的对应关系较符合，且轴向侧压比的改变不会影响应力差及塑性区的形态特征。数值模拟结果与理论分析结果较符合，进一步验证了理论分析的正确性。

4 工程实例分析

4.1 数值模拟模型

宁煤矿区羊场湾煤矿目前主采2号煤层的160206工作面，工作面距地面垂直埋深为592 m，工作面上临120212工作面采空区，工作面走向长度为470 m，倾向长度为195 m。160206工作面走向长度为80 m，倾向长度为227 m，回风巷和运输巷长度分别为2 387和2 471 m。煤层开采平均厚度为9.3 m，属于近水平煤层；采煤方法为走向长臂后退式放顶煤采煤法，采高为4 m，放煤厚度为5.3 m。2号煤层顶板主要由粉砂岩、中粒砂岩组成，底板主要由泥岩、粉砂岩、中砂岩构成。160206回风巷工作面布置及煤层顶底板柱状图如图6所示。

图6 160206工作面布置及煤岩层顶底板柱状图Fig.6 160206 working face layout and coal strata roof and floor histogram

160206回风巷采用“左旋无纵肋螺纹钢锚杆+锚索+钢筋网”的组合支护技术，原支护参数如图1所示。120212工作面停采后，在采空区四周形成残余支承压力带。在160206工作面推进过程中，工作面四周形成的采动支承压力带与残余支承压力带相互叠加，形成叠合支承压力带。在高应力集中影响下，回风巷围岩在服务期间内出现非对称大变形、冒顶、网兜、锚杆索失效等现象，现场破坏图如图7所示。从破坏情况来看，巷道顶板煤壁侧多次出现大面积漏顶，据现场调查结果可知，漏顶现象已经多次影响正常安全生产。钻孔窥视结果也表明，煤壁侧顶板出现大量横向、纵向、斜交裂隙，部分位置出现明显离层。

图7 160206工作面原支护方案及现场破坏图Fig.7 160206 working face original support scheme and field failure pictures

结合羊场湾矿160206 工作面地质条件，建立FLAC3D大型数值模拟模型，模型长×宽×高为850×1 100×150 m，回风巷道宽、高分别为5 m和4 m，为消除尺寸效应，在工作面四周预留150 m边界煤柱。模型网格数量约为150万个，在重点研究位置采用局部网格加密。模型四周及底部边界采用位移约束，顶部边界采用应力约束。数值计算采用M-C强度准则，采空区充填采用双屈服垮落模型。x、y、z方向施加的荷载分别为13.00、17.88和16.25 MPa。

模型开挖顺序依次为120212服务巷道、120212工作面、160206服务巷道、160206工作面。数值模拟模型及岩石力学参数如图8所示。

图8 数值模拟模型及岩石力学参数Fig.8 Numerical simulation model and rock mechanics parameters

4.2 回风巷主应力差及塑性区分布特征

由理论分析可知，围岩主应力差分布与塑性区形态分布具有一一对应关系，主应力差可以更好地表征围岩的变形破坏特征。因此，在工作面推进距离为0、350、400、450、500、550、600、650 m共8个位置布置监测点，通过对回采巷道整个服务周期内主应力差演化规律进行分析，揭示回采巷道围岩变形破坏机理及主控因素。

工作面推进全周期内主应力差三维分布云图如图9所示。从图9可知，工作面推进过程全时域可分为3个主要阶段：

1) 实体煤侧推进段。工作面的开采导致四周形成主应力差集中，工作面四周主应力差分布呈“马鞍形”分布，该区域巷道仅受采面前方采动影响，回风巷主应力差集中水平相对较低。

2) 实体煤采空区侧过渡段。该阶段为上区段残余支承压力的初期扰动阶段，回风巷侧开始受到上下区段叠加采动影响，产生主应力差集中，其集中程度明显高于工作面其余3侧的集中程度。

3) 采空区侧推进段。该阶段为叠加采动影响的剧烈影响阶段，回风巷围岩主应力差急剧增高，工作面煤柱侧主应力差凸起程度更加明显。

为获得叠加采动影响巷道“采动应力与破坏区演化”的内在联系，有必要对巷道围岩不同采动时域下的主应力差演化规律、围岩破坏区分布范围及形态特征进行深入研究。选取工作面前方10 m和20 m位置，采用Cutting Plane功能调取不同工作面推进度下围岩主应力差与塑性区分布图谱，结果如图10所示。

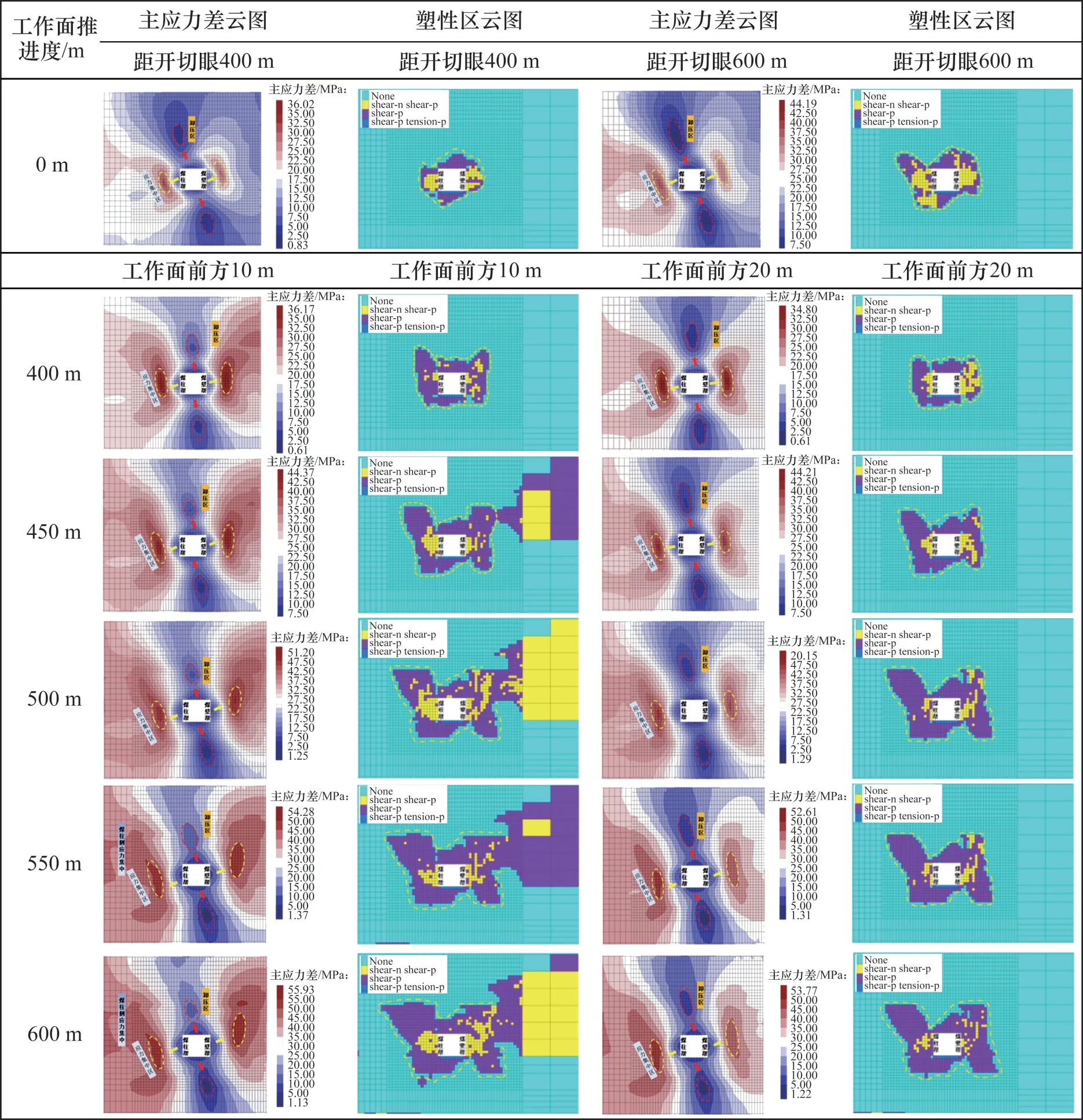
图10 不同工作面推进度下工作面前方主应力差及塑性区分布云图Fig.10 Nephogram of difference of principal stress and distribution of plastic zone in front of working face under different advance degrees

由图10可知，当工作面未推进时，距开切眼400 m处主应力差受上区段采空区影响呈偏转分布，主应力差与塑性区形态均为类蝶形。距开切眼600 m处，回风巷位置处于上区段采空区中部，此时，受到上区段影响十分强烈，巷道周边主应力差集中程度大幅上升，应力及塑性区形态均为明显的蝶形。

从400、450、500、550、600 m主应力差云图分布来看，工作面前方10 m处的回风巷围岩主应力差在叠加采动影响下较掘进阶段急剧升高，且随着工作面推进度向上区段采空区中部靠近，主应力差值峰值呈大幅上升趋势，工作面前方20 m处的主应力差值集中程度比10 m的略小，且在高叠加应力差场下，主应力差分布形态呈蝶形。同时，巷道由于浅部破碎严重而无法承担高应力差，致使高应力差峰值向围岩深部转移，因此，在巷道围岩浅部存在应力差卸压区。

从塑性区分布云图来看，塑性区与主应力差在形态和方向上的演化规律存在密切关系。工作面前方10 m处由于二次采动影响导致围岩蝶形塑性区进一步扩大，随着工作面推进，工作面前方10 m处的塑性区开始与煤壁贯通，工作面前方20 m处的塑性区范围比前方10 m处的小。

综合上述分析可以看出，在叠加采动影响下，160206回风巷产生高主应力差集中，致使围岩主应力差分布呈蝶形分布，随着工作面推进，蝶叶偏转角稳定在45°左右，主应力差集中致使围岩产生约45°蝶形破坏，蝶叶的偏转导致顶板煤壁帮一侧塑性区面积大于煤柱帮塑性区面积，这也是回风巷产生非对称大变形破坏的原因。

4.3 巷道围岩控制原理与支护优化

煤矿巷道冒顶事故分为原生赋存型冒顶和应力主导型冒顶[24]，应力主导型冒顶是由于围岩开掘或回采过程中破坏了原岩应力平衡状态，应力环境改变导致围岩产生不同程度破坏而引起支护失效冒顶。大量研究表明[25-26]，在当前支护技术水平下，支护阻力与扰动应力并非处于同一量级，即支护密度增加对巷道塑性区的减少程度十分有限。由悬吊理论可知，支护体的主要作用是将易冒落岩体锚固在深部未松动岩体之上，增强较软弱岩层的稳定性。

由数值模拟结果分析可知，回风巷超前段在高应力差作用下形成蝶形塑性区，且由于蝶叶的偏转导致煤壁侧顶板的塑性破坏程度比煤柱侧顶板的大。因此，叠加采动巷道控制的主要思路为：1) 调整高主应力差集中部位。通过钻孔卸压使围岩形成高应力卸压带，迫使高应力集中区向围岩深部转移。2) 支护体长度要大于破坏岩体长度，要对蝶叶易扩展部位进行重点支护。3) 支护体可承载质量要大于破坏岩体质量。4) 支护体延伸量要大于破坏围岩膨胀变形量。5) 支护体要有一定的抗冲击能力，防止支护体由于瞬时冲击形成破坏。

因此，结合羊场湾矿实际生产地质条件，提出超前段钻孔卸压+非对称长短锚杆索+单体液压支柱+全断面混凝土喷射的联合协同支护技术。针对现场破坏情况及数值模拟分析结果，提出主要补强支护措施为：1) 在煤壁帮顶板和煤柱帮顶板补打1根直径×长度为28.6 mm×8 300.0 mm的锚索，煤壁帮上下两端、煤柱帮下端各补打1根直径×长度为21.8 mm×6 300.0 mm的锚索，加强支护方案示意图如图11所示。2) 在巷道超前段90 m范围内安放高强无反复支撑单元支柱，通过单元支柱的强支撑作用来承担部分岩层的质量。3) 工作面超前位置布置卸压孔洞群，煤壁侧顶板每隔10 m、煤柱侧顶板每隔20 m布置1组长30 m、直径为79 mm的钻孔。4) 巷道采用全断面喷射混凝土，喷射厚度为70 mm，喷射混凝土强度等级为C20，通过喷射混凝土使巷道围岩形成拱式承载结构。

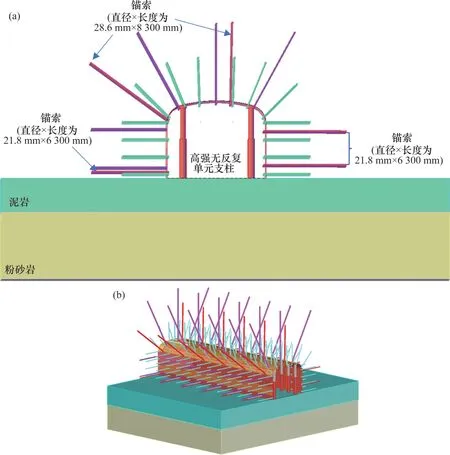
图11 加强支护方案示意图Fig.11 Schematic diagram of strengthening support scheme

进行加强支护前，巷道顶板最大下沉量、最大漏顶高度、最大底臌量分别为1.2、2.3、1.0 m。在现场进行工业性试验后，选取距开切眼515、595、695 m处布置3组巷道表面位移测站，经观测统计，巷道在之后的整个服务周期内3组测站围岩各处的最大变形量分别为495、475、375 mm，围岩变形量大幅下降，冒顶隐患大幅减少，巷道稳定控制效果良好。