高心墙堆石坝材料本构模型计算的适用性研究

程瑞林，汪泾周，范钦煜，湛正刚，周伟,3，马刚,3

(1.武汉大学 水资源工程与调度全国重点实验室，湖北 武汉，430072；2.中国电建集团 贵阳勘测设计研究院有限公司，贵州 贵阳，550081；3.武汉大学 水工程科学研究院，湖北 武汉，430072)

近年来，随着堆石坝设计理论的发展与高坝填筑技术的革新，我国高堆石坝的建设水平逐渐从200 m级上升到300 m级。相比于早期建设的中低土石坝，已建高堆石坝监测结果表明，目前的堆石坝设计理论在高坝坝体的应力、变形控制方面仍存在不足，高堆石坝数值计算精度较低问题突出。为解决这一问题，学者们主要从材料本构关系和模型参数确定2个方面展开了研究。在对材料本构的研究方面，ALONSO等[1-4]提出了BBM(barcelona basic model)模型和RM(rock-fill model)模型，并将其用于预测Beliche坝的变形和心墙孔隙压力。姚仰平等[5-6]在修正剑桥模型基础上通过引入统一硬化参数，对修正剑桥模型进行改进，使其能够统一反映土体的剪胀和剪缩现象，并建立了考虑颗粒破碎的粗粒土本构模型。PASTOR等[7]提出了P-Z广义塑性模型，该模型直接基于剪胀方程定义塑性流动方向和加载方向，并能灵活地定义不同加载条件下的塑性模量。董威信[8]在P-Z模型的基础上建立了MPZG模型，将临界状态理论和状态参数引入P-Z模型中。在对模型参数的研究方面，一些学者致力于改进堆石料材料参数的获取方法。孔宪京等[9-10]研发了超大型三轴仪，通过降低缩尺程度提高了参数的准确性。周伟等[11-13]采用连续离散耦合分析方法对堆石料进行数值试验，分析了筑坝堆石料的缩尺效应，提高了参数的合理性。另一些学者则致力于改进反演方法以便从监测资料中获得更精准的材料参数。朱晟等[14]提出了基于增量分析的堆石坝瞬变-流变联合反演方法，并结合坝内水管式沉降仪和测斜沉降管对南欧江7级面板坝进行了联合反演分析。杨荷等[15-16]提出了基于改进响应面法的反演分析方法，并运用该方法进行了水布垭面板坝的材料参数的反演计算。尽管学者们进行了大量关于单一本构模型及其参数取值方法的研究，但对于多种本构模型在实际高堆石坝计算中的优劣与适用性评价研究较少，新建高堆石坝工程究竟应采用何种模型进行计算评估仍有待考虑。本文以此为出发点，选择非线性弹性的邓肯E-B模型、传统弹塑性的沈珠江双屈服面模型和基于广义塑性框架的MPZG模型这3类高堆石坝计算中较具代表性的模型，采用室内试验方法得到的参数，对筑坝堆石料在三轴排水条件下宏观力学响应进行验证，并对坝体应力、变形进行计算，探讨这3种模型在高心墙堆石坝应力、变形计算中的适用性问题，以期为其他高心墙堆石坝工程的应力、变形计算提供借鉴与参考。

1 计算理论

1.1 邓肯E-B模型

DUNCAN等[17]基于双曲线模型进行了应力-应变关系的非线性分析，并提出了E-ν模型。由于E-ν模型在实际应用时计算得到的泊松比通常大于试验测定结果，DUNCAN在E-ν模型基础上采用切线体积模量代替切线泊松比，得到了E-B模型。在该模型中，砂土的弹性模量和体积模量采用切线值进行计算，切线模量Et和切线体积模量Bt计算式分别如式(1)和式(2)所示。

式中：S为应力；Ei为初始切线模量；σ1和σ3分别为大、小主应力；Rf为破坏比，表示砂土实际破坏强度与极限破坏强度的比值；Pa为大气压强；K、n、Kb和m均为量纲一模型参数；c和ϕ分别为Mohr-Coulomb强度破坏准则中的黏聚力和内摩擦角，其中，黏聚力一般认为是常数，内摩擦角则可利用材料参数ϕ0和Δϕ及围压σ3采用非线性模型ϕ=ϕ0-Δϕlg(σ3/Pa)计算得到。此外，为模拟砂土在加卸载时宏观响应的差异性，砂土卸载时的切线模量可采用卸荷模量Eur进行计算。

式中：Kur为量纲一模型参数。

1.2 沈珠江双屈服面模型

沈珠江双屈服面模型属于弹塑性模型[18]，分别采用椭圆曲线和幂曲线作为其屈服面，屈服函数定义为

式中：p和q分别为平均主应力和广义剪应力；r和s为根据土性特点调整的屈服面参数，对于粗粒土，二者均可取值为2，对细粒土可分别取2和3。根据弹塑性力学的基本原理，砂土的变形Δε即为弹性部分变形Δεe和塑性部分变形Δεp之和，二者可分别按照胡克定律和正交流动法则计算。

式中：C为弹性刚度张量，可由切线模量Et和切线泊松比μt计算得到；Δσ为应力张量增量；Δf1和Δf2分别为屈服函数f1和f2的增量；A1和A2分别为相应塑性系数，反映2个屈服面各自产生的塑性应变的大小，可按式(7)计算。

式中：η=q/p，为应力比；Kur和Gur分别为按照卸荷模量Eur和卸荷泊松比μur计算得到的体积模量和剪切模量；切线模量Et和卸荷模量Eur可参照E-B模型分别按照式(1)和式(3)进行计算，卸荷泊松比μur取经验值0.3，切线泊松比μt可以依照式(8)计算。

式中：cd、nd、Rd和Rf均为模型参数。

1.3 MPZG模型

PASTOR等[7]提出的P-Z模型是一种广义塑性模型，MPZG模型则为在其基础上引入临界状态理论和状态参数后的改进模型。在MPZG模型中，同样将砂土的应变增量分解成弹性和塑性应变增量2个部分。

对于弹性部分，可按下式计算体积模量Kev和剪切模量Ges：

式中：K0和G0分别为弹性阶段的体积模量和剪切模量；e为孔隙比；Pa为大气压强。

对于塑性部分，有

式中：Δλ为塑性乘子；De为弹性张量；ngL/U为塑性流动方向；nf为加载方向；HLU为塑性模量。

MPZG模型的剪胀方程采用剑桥模型剪胀方程的修正形式，即

式中：η为应力比；αg和mg为模型参数；Mg为临界状态的应力比；Md为Mg的修正值；ψ为状态参数，能够反映土体状态对应力、应变的影响。

式中：ec为当前有效应力对应的临界孔隙比；eΓ、λc和ζ均为模型参数，对于砂土材料ζ，可依据经验取0.7。

根据剪胀方程可得p-q应力空间中的塑性流动方向ngL为

加载方向nf采用与塑性流动方向相似的格式，

式中：αf为模型参数；Mf为峰值应力比。塑性模量HLU分别考虑加载和卸载2种情况。加载时，塑性模量HL可按式(16)计算。

式中：H0为模型参数；Hf、Hv、HDM分别为描述偏应变映射法则、相变转换线相关特性及边界面塑性映射规则的系数，三者可分别按照式(18)、式(19)、式(20)进行计算。

式中：HL0、βH、mb、γ均为模型参数。卸载时，塑性模量可按式(21)计算。

式中：HU0为模型参数；ηU为卸载时的应力比；Hden为表征粗粒土压密和硬化效应的硬化项，可根据体积应变εv和模型参数rden按式(22)计算。

2 计算模型与参数

RM心墙堆石坝坝顶高程为2 907.00 m，坝顶宽为18 m，河床段心墙建基面高程为2 592.00 m，最大坝高315.00 m，防浪墙顶高程为2 908.20 m。坝顶长为650.20 m，坝体最大底宽约1 250 m。大坝上游坡比为1:2.1，在高程2 860.00 m和2 810.00 m处分别设置5 m宽马道，下游综合坡比为1:2.0。防渗心墙采用直心墙，心墙顶宽5 m，上下游坡比为1:0.23，心墙上下游分别设置2层反滤层，上下游反滤层与堆石体之间设置过渡区。心墙与岩石基础面之间设置接触黏土层和混凝土盖板，以适应岸坡剪切变形，防止接触冲刷。心墙堆石坝典型断面图见图1。

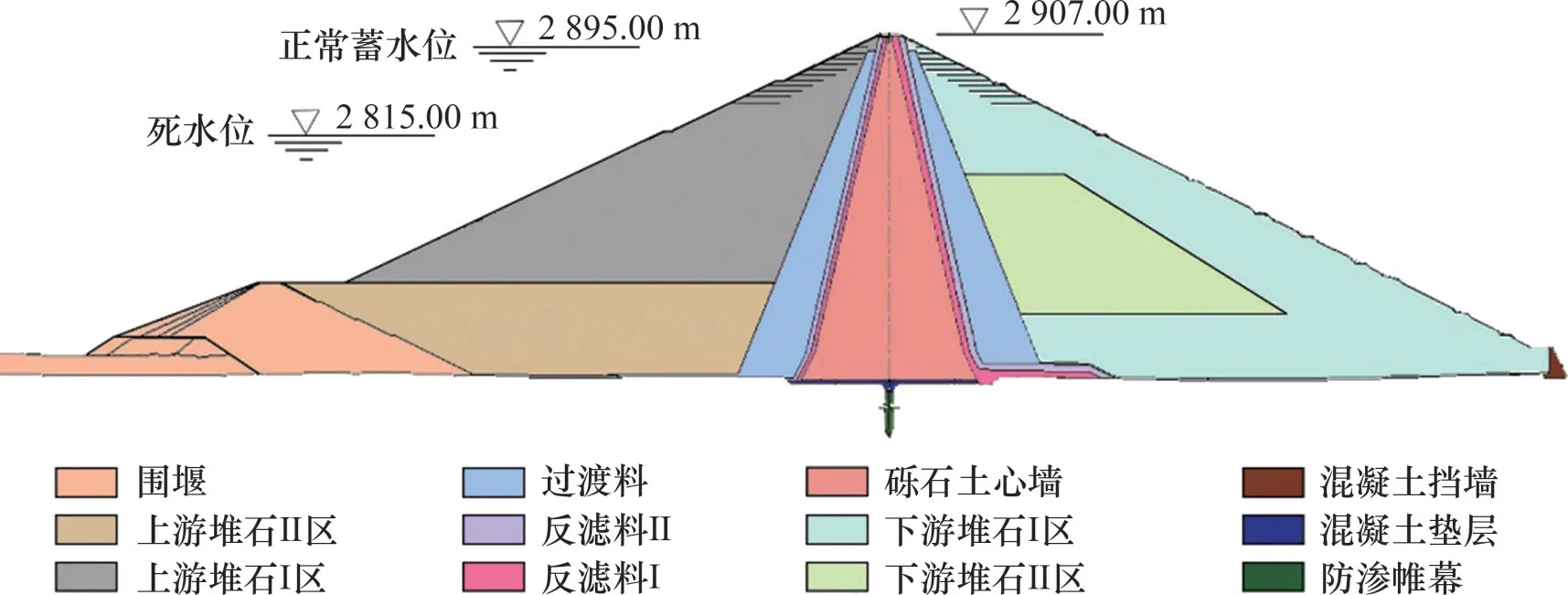
图1 心墙堆石坝典型断面图Fig.1 Typical sectional view of core wall rockfill dam

2.1 计算模型及工况

三维网格模型沿横河方向单元边长均为20 m，共包括16 703个结点和18 623个单元。图2和图3所示分别为整体三维计算网格及其顺河向最大断面剖面图。计算工况为坝体分级填筑至坝顶高程2 907 m，并蓄水至正常蓄水位2 895 m，模拟的填筑施工和蓄水过程如图4所示。

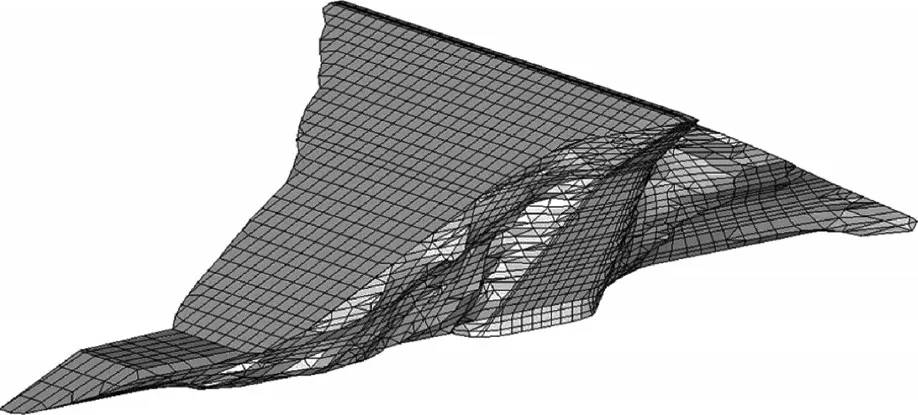
图2 三维网格模型Fig.2 Three-dimensional grid model

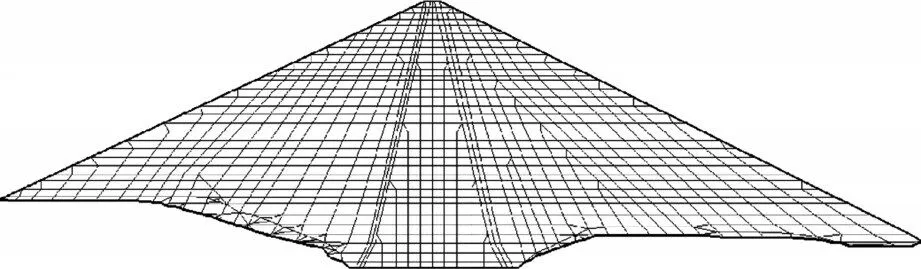
图3 三维网格模型顺河向最大断面剖面图Fig.3 The maximum section view of the three-dimensional mesh model along the river

2.2 计算参数

常规三轴试验所得坝体堆石料Ⅰ、堆石料Ⅱ和过渡料关于邓肯E-B模型、沈珠江双屈服面模型和MPZG模型这3种模型的计算参数分别如表1～3所示。

表1 邓肯-张E-B模型参数Table 1 Duncan-chang E-B model parameters

表2 沈珠江双屈服面模型参数Table 2 Shen Zhujiang double yield surface model parameters

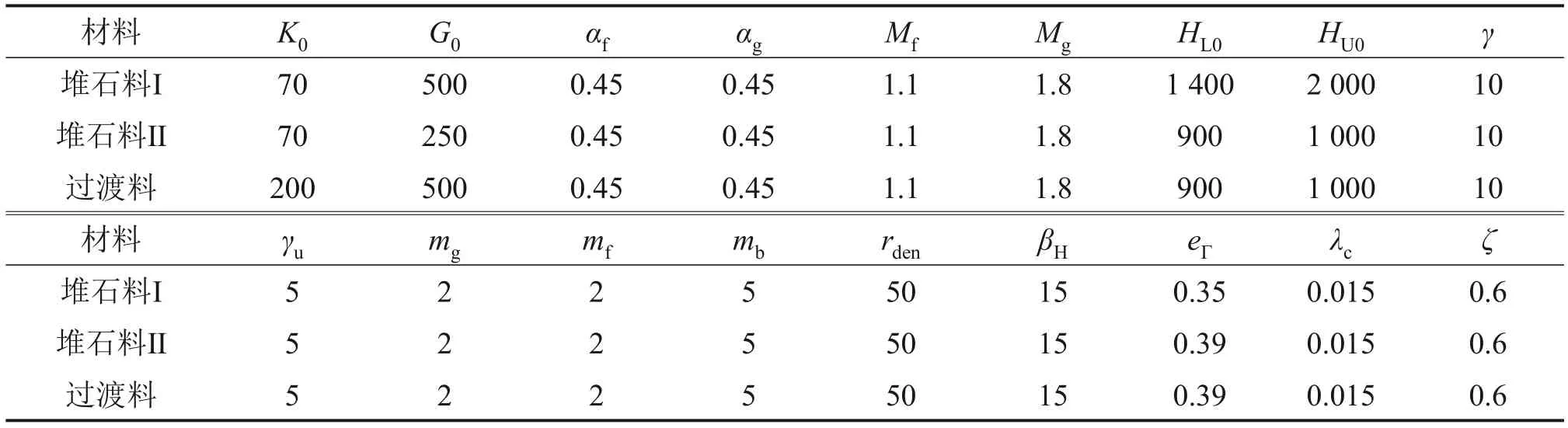
表3 MPZG模型参数Table 3 MPZG model parameters

3 不同本构模型适用性分析

3.1 三轴应力路径的宏观力学响应分析

分别采用邓肯E-B模型、沈珠江双屈服面模型和MPZG模型及前文所述的模型参数对堆石料Ⅰ、堆石料II、过渡料进行三轴排水试验的数值模拟，试验围压σ3分别设置为400、1 200和2 000 kPa，得到宏观响应曲线，分别如图5～7所示，其中沈珠江双屈服面模型简称为SZJ模型。

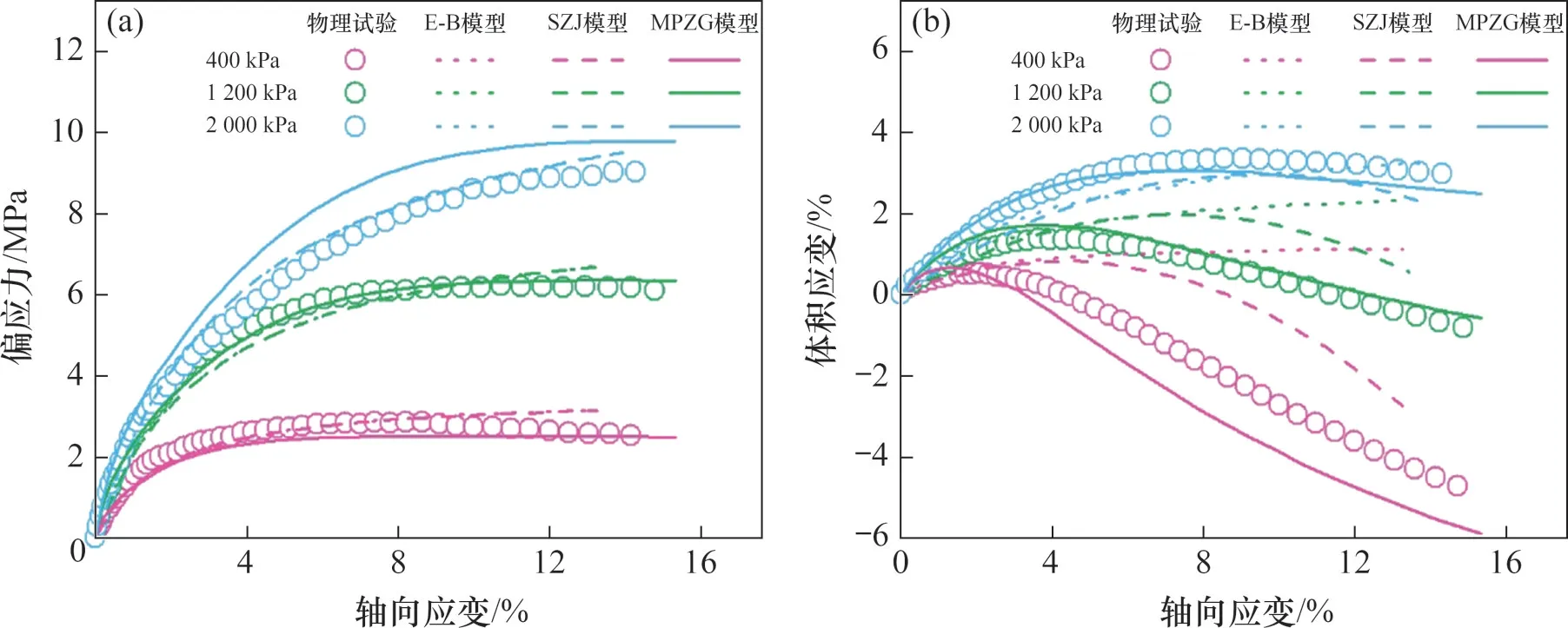
图5 堆石料I常规三轴排水试验结果对比Fig.5 Comparison of conventional triaxial drainage test results of rockfill I

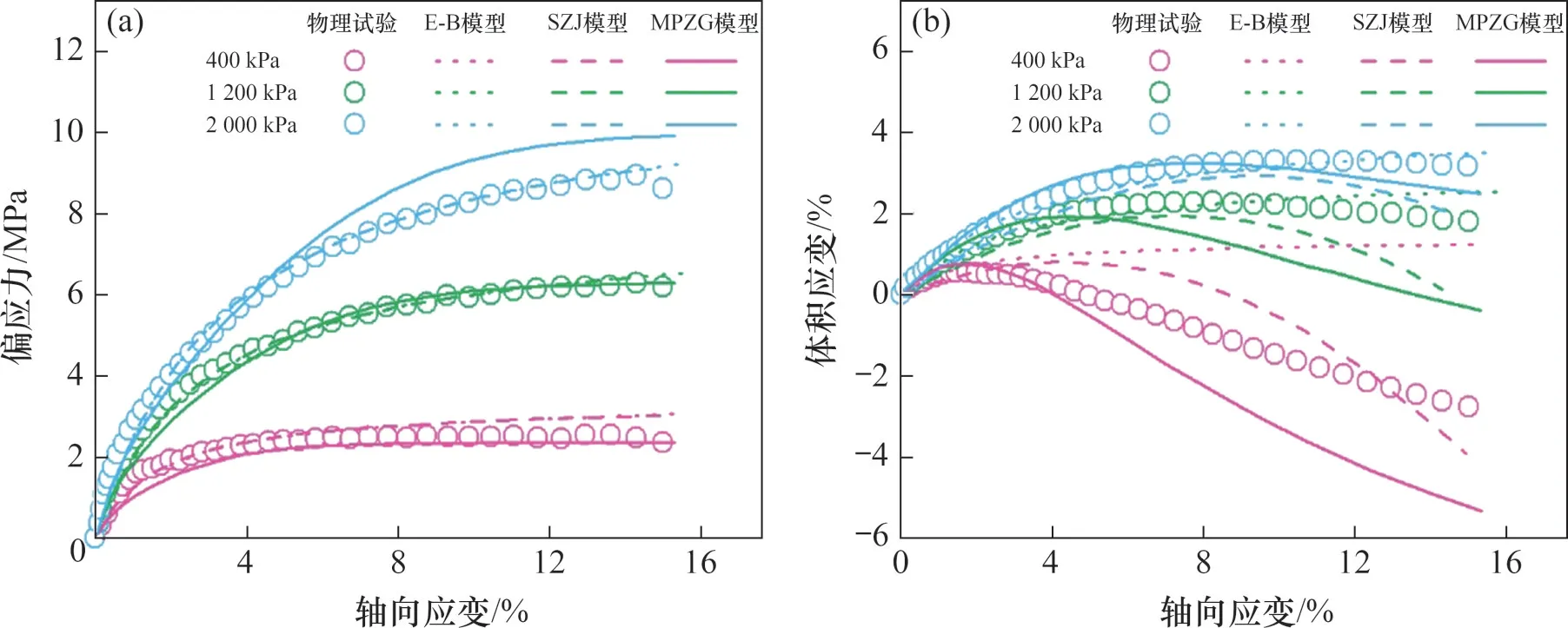
图6 堆石料II常规三轴排水试验结果对比Fig.6 Comparison of conventional triaxial drainage test results of rockfill II

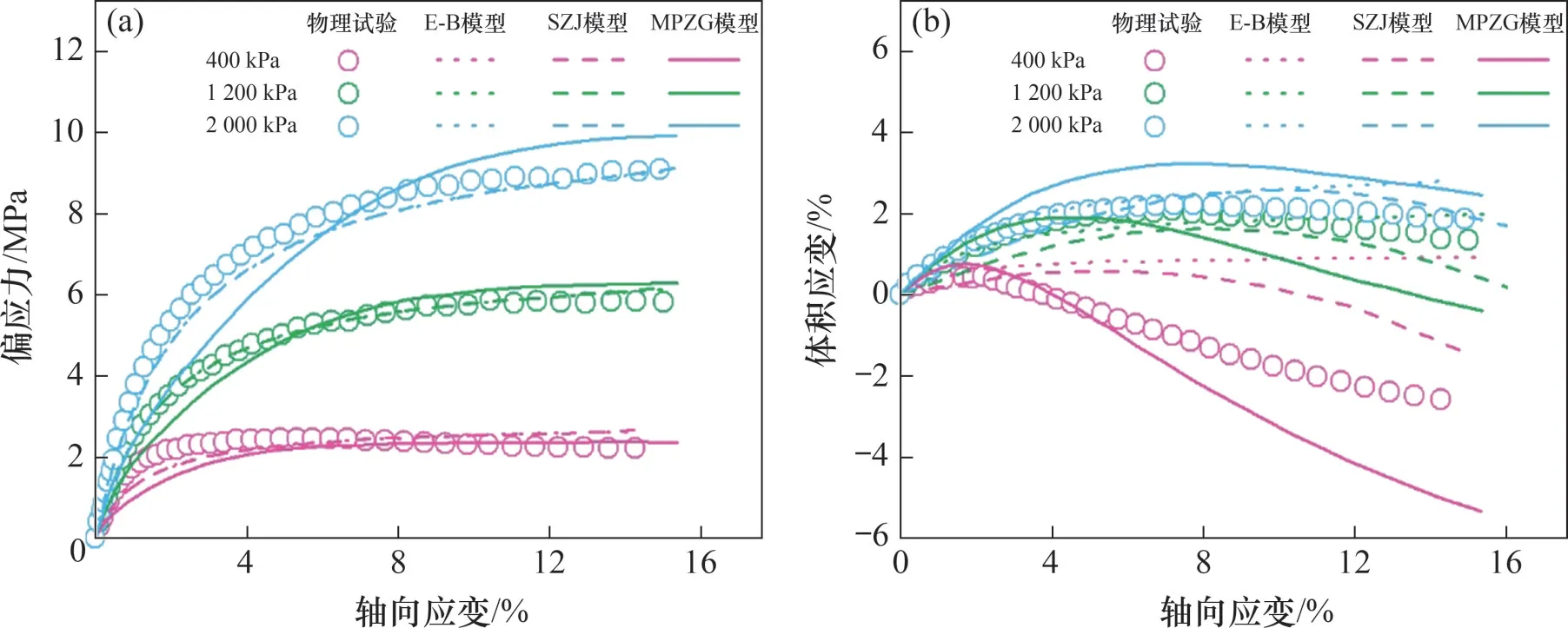
图7 过渡料常规三轴排水试验结果对比Fig.7 Comparison of conventional triaxial drainage test results for transition materials

从试验结果来看，不同试验堆石料的宏观力学响应规律一致。在应力响应上，3种模型均能较好地反映堆石料的应力响应，在较高围压下，MPZG模型的拟合程度稍差于邓肯E-B模型和沈珠江双屈服面模型的拟合程度。在体积应变响应上，邓肯E-B模型不能反映材料的剪胀特性，在低围压下拟合效果很差；沈珠江双屈服面模型和MPZG模型虽然能反映材料的剪胀性，但在低围压下，二者剪胀程度也存在差异。在高围压下，堆石料的体积响应以体缩为主，3种模型均能较好地吻合。综合而言，较高围压下的邓肯E-B模型和沈珠江模型宏观力学响应比MPZG模型的略优，在较低围压下，沈珠江双屈服面模型和MPZG模型的宏观力学表现明显优于邓肯E-B模型的宏观力学表现。

3.2 坝体应力分析

分别采用邓肯E-B模型、沈珠江双屈服面模型和MPZG模型及前文所述的模型参数对如美心墙坝三维有限元模型进行满蓄期的有限元计算，得到坝体大主应力、小主应力等值线分别如图8和图9所示。

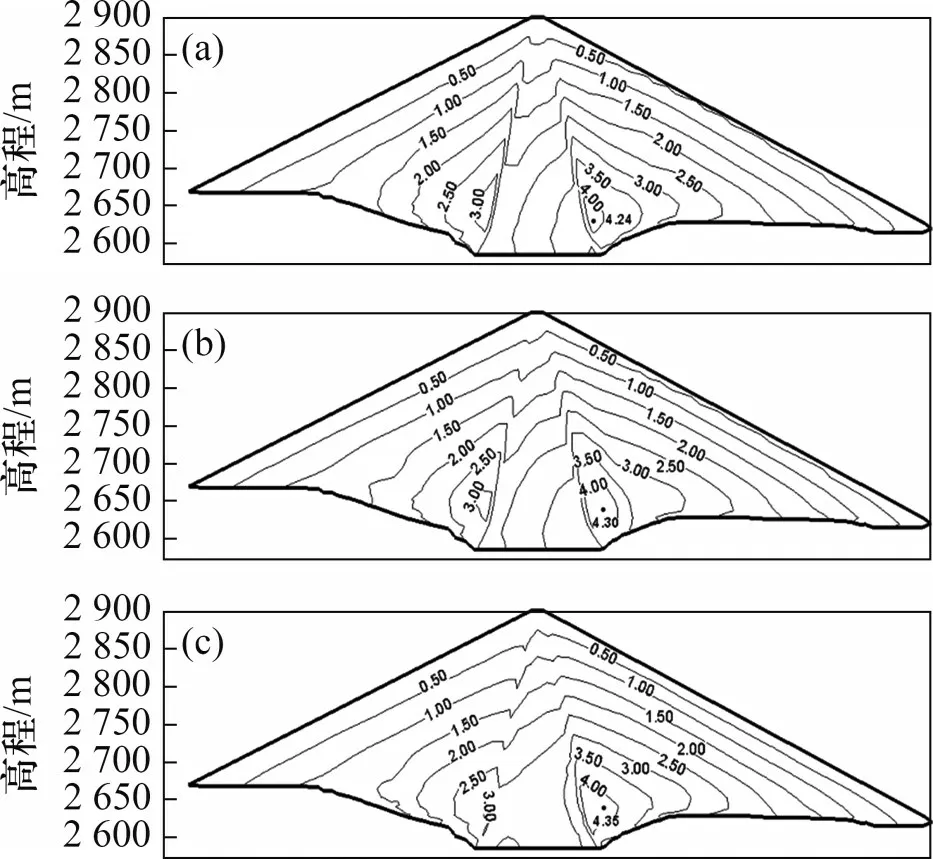
图8 满蓄期坝体大主应力分布Fig.8 Distribution diagram of major principal stress of dam body in full storage period

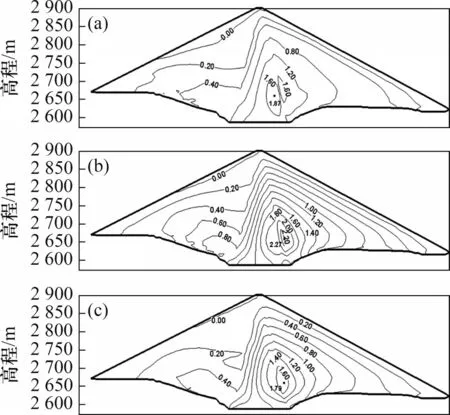
图9 满蓄期坝体小主应力分布Fig.9 Distribution diagram of minor principal stress of dam body in full storage period

从计算结果来看，3种模型的应力计算结果相当，应力分布规律基本一致。其中，3种模型的大主应力最大值均出现在心墙下游侧和过渡料部位坝底与建基面交界处，分别为4.24、4.30和4.35 MPa；小主应力最大值均出现在心墙内下游下部，分别为1.87、2.27和1.79 MPa。在应力分布上，应力等值线基本平行于坝坡，由外向内逐渐增大，上游应力低于下游应力且表层出现小范围的拉应力区，E-B模型计算所得拉应力区范围略大于其他2种模型的拉应力区范围。

3.3 坝体变形分析

分别采用邓肯E-B模型、沈珠江双屈服面模型和MPZG模型及前文所述的模型参数对如美心墙坝三维有限元模型进行满蓄期的有限元计算，得到坝体顺河向位移和沉降等值线分别如图10和图11所示。

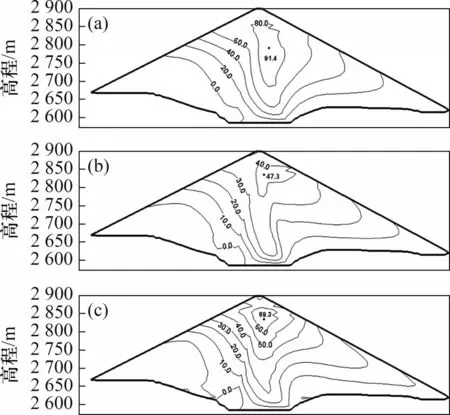
图10 满蓄期坝体顺河向位移等值线图Fig.10 Contour map of displacement along river of dam body in full storage period

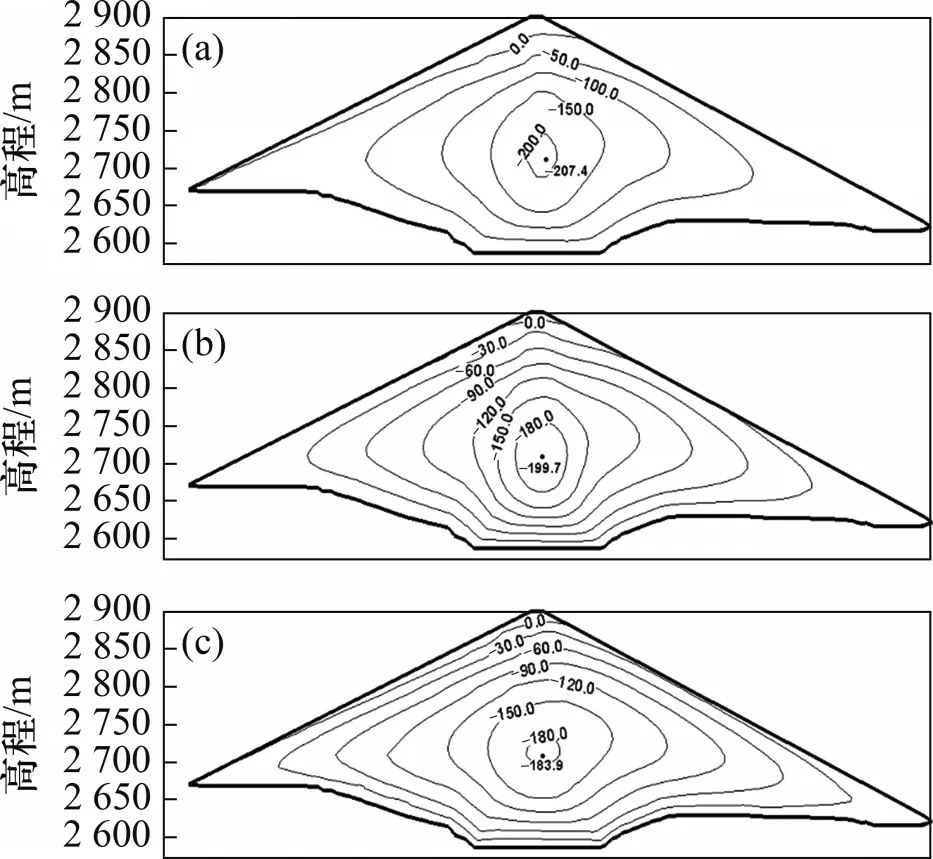
图11 满蓄期坝体沉降等值线图Fig.11 Contour map of settlement of dam body in full storage period

从计算结果来看，3种模型的坝体变形计算总体规律一致，但具体数值尤其是顺河向位移差异明显。3种模型的顺河向位移最大值均出现在坝体中上部，分别为91.4、47.3和69.3 cm；坝体沉降最大值同样位于坝体中部，分别为207.4、199.7和183.9 cm。在变形分布上，顺河向位移等值线呈“V”形与上下游坝坡斜交，在近坝顶处出现闭环，且上游坝坡位移梯度大于下游位移梯度，沉降变形呈现同心环状分布，上下游近似对称分布，自内向外沉降逐渐减小。

3.4 模型适用性讨论

首先，从宏观力学方面来看，在三轴试验条件下，3种模型的应力响应比较接近，均能反映堆石料的宏观力学特征，因而，在坝体应力计算中，3种模型得到的最大和最小主应力分布均较接近。但是在变形响应上，邓肯E-B模型不能考虑堆石料的剪胀特性，中低围压下的体积应变与室内试验结果相差较大，沈珠江双屈服面模型和MPZG模型均能反映堆石料的剪胀特性，二者所得结果与室内试验结果更接近，因而，在坝体变形计算结果尤其是顺河向位移上，沈珠江模型和MPZG模型计算结果更接近实际结果。可见，沈珠江双屈服面模型和MPZG模型变形计算结果更具有说服力，更适用于堆石坝有限元计算分析。

其次，从应力、变形分布上看，尽管不同工程的坝体应力、变形有所差别，但具有大致相同的分布特点[19]。综合参考文献[19-23]中高心墙堆石坝坝体应力、变形结果，高心墙堆石坝应力、变形的一般规律为：

1) 在应力方面，心墙区存在明显的拱效应，由于心墙料比坝壳料软，心墙部分的相对变形大，坝壳堆石料部分的相对变形小，心墙与坝壳料交界处由于变形不协调发生应力重分配，使得心墙部分的应力转移向两侧坝壳料，显著降低了心墙区的压应力；同时，心墙两侧的过渡料附近则出现密集的应力等值线。

2) 在变形方面，由于心墙料比坝壳堆石料软，更容易发生明显的变形。在顺河向位移上，受两边不对等的水压作用，水平位移基本出现在下游，最大值出现在心墙中部或下游侧坝壳料中上部；在竖直沉降上，其最大值出现在心墙内，大约位于坝高中部。

结合本文3种模型的应力、变形计算结果可知，3种模型得到的应力、变形分布规律均满足堆石坝应力、变形的一般性分布规律，表明这3种模型都能为高心墙堆石坝建设提供参考。

此外，由于E-B模型较为简单，较早地被引入到堆石坝工程设计中，更容易通过工程类比等方法从已建工程中获得材料参数。由此可见，在高心墙堆石坝建设初期，如果缺少试验数据来确定材料参数，可以通过工程类比方法从已建工程中获取，进行初步的应力、变形合理性分析，为设计方案比选提供计算依据。

表4所示为我国几座典型心墙堆石坝的沉降监测值统计结果，沉降最大值相对坝高的百分数均在1%以上，而本文3种模型的最大沉降计算结果为最大坝高的0.66%～0.58%，均小于已建高坝沉降监测值，其原因如下：一是本文直接采用了由室内缩尺级配试验得到的材料参数，忽略了堆石料缩尺效应对材料参数的影响[11]；二是因为本文没有考虑流变、湿化等因素引起的堆石料力学性能的劣化，高估了堆石料的力学性能[24-25]。在实际工程计算中，应考虑这两者的影响才能得到更合理的计算结果。

表4 中国典型高心墙坝沉降监测值统计Table 4 Settlement monitoring statistics of typical high core wall dams in China

综上分析可知，本文所采用的3种模型计算得到的坝体应力、变形分布均符合一般性认识规律，均能为工程设计施工提供一定参考，其中E-B模型不能反映堆石料的剪胀特性，在坝体变形计算上有所欠缺，而沈珠江双屈服面模型和MPZG模型等弹塑性模型能反映堆石料的剪胀特性。在工程建设初期，可通过工程类比获取E-B模型参数，进行工程建设的早期评价，初步论证方案的可行性。

4 结论

1) 3种模型均能较好地模拟应力响应，但在体积响应的模拟上均存在不同程度的缺陷。整体上看，较高围压下的邓肯E-B模型和沈珠江模型的宏观力学表现稍优于MPZG模型的宏观力学表现，在较低围压下，沈珠江双屈服面模型和MPZG模型的宏观力学表现明显优于邓肯E-B模型的宏观力学表现。

2) 3种模型的应力、变形计算结果整体上均符合一般规律。3种模型中大、小主应力分布相似且数值相近。邓肯E-B模型的变形计算值最大，沈珠江双屈服面模型的顺河向位移计算值较小，MPZG模型的沉降计算值较小。

3) 邓肯E-B模型和沈珠江双屈服面模型形式更简单，在工程上应用较多；MPZG模型和沈珠江双屈服面模型在理论上能反映堆石料的剪胀特性。3种模型均能反映高土石坝的应力、变形分布特点，建议在建设初期采用邓肯E-B模型进行比选，在建设后期采用沈珠江双屈服面模型或MPZG模型分析成果作为结构设计的重要依据。