基于改进自适应遗传算法的小径短绳自动打捆机步进电机PID控制
2024-02-29代健超孙志军杜诚杰
代健超,孟 婥,孙志军,杜诚杰
(东华大学 机械工程学院, 上海)
目前绳制品的包装方式以绳辊绕绳为主,这种包装方式更适用于较长的绳制品,对10 m以下小径短绳包装用绳辊方式而言会大大增加包装成本。自动绳缆打捆机能实现小径短绳缆的自动打捆,即按照预定长度将长绳进行八字打捆并裁剪,打捆过程中横向打捆电机和纵向打捆电机的控制精度直接影响绳捆的包装品质,要提高打捆步进电机的精度需要高精度控制算法。李萌等[1]从自适应编码、自适应选择、自适应交叉、自适应变异4个方面对遗传算法进行了自适应优化,获得了良好的控制效果,但每进化一代都要进行4种自适应计算,算法计算过程复杂,计算速度较慢。Yang[2]为解决柔性作业车间调度问题,设计了具有IPOX(improved precedence operation crossover)交叉和多点交叉2种交叉方式的改进遗传算法,采用并行双链编码对操作顺序和机器选择2个问题并行求解,但缺少自适应设计,遗传算子的交叉率PC=0.8,变异率Pm=0.05,容易引起遗传算法的退化现象。徐梦颖等[3]针对移动机器人路径规划问题设计了一种免疫克隆自适应遗传算法,提高了求解精度,加快了收敛时间,但容易陷入局部最优。
针对上述问题,本文建立打捆机横向打捆电机模型,分析并解决了经典遗传算法盲目进化和经典自适应遗传算法易陷入局部最优的问题,提出具有更好收敛能力并能削弱退化现象的改进自适应遗传算法,加快了算法的收敛速度,降低了算法陷入局部最优的概率,提高了自动绳缆打捆机的打捆精度。
1 小径短绳自动打捆机原理分析
图1为小径短绳自动打捆机示意图。由图1可知:气动生头机械手由薄型气缸、气爪、锯齿夹爪和电热熔刀组成,负责将绳头压入绕臂的夹紧块和剪断绳缆;绕臂是八字打捆的核心部分,绳缆的打捆和生头都在绕臂上完成;打捆部件由绕臂、绕臂支架和绕臂支架所在的滚珠丝杠导轨组成的装配体,实现纵向打捆和横向打捆;排线器则负责横向打捆时引导绳缆和实现绳缆与生头气动机械手夹爪的对位;环形凹槽导轨与绕臂支架所在的滚珠丝杠导轨下边安装万向球接触,为打捆部件提供支撑力,防止打捆部件偏摆振动;电滑环在打捆部件旋转时防止电线缠绕。
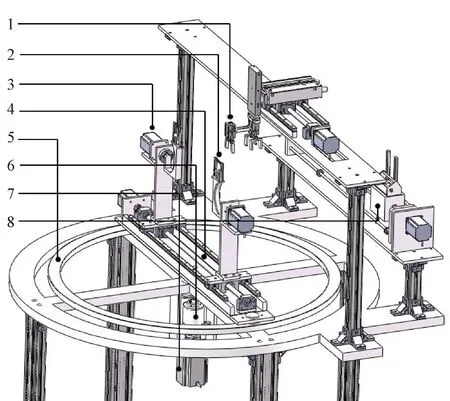
注:1-气动生头机械手;2-绕臂;3-绕臂电机;4-打捆部件;5-环形凹槽导轨;6-电滑环;7-纵向打捆电机;8-排线器。图1 小径短绳自动打捆机Fig.1 Automatic strapping machine of small diameter short rope
绳辊的小径短绳经过张力采集机构的滚轮,然后从排线器的导向孔穿过并夹紧在绕臂的夹块上,利用纵向打捆电机驱动打捆部件转动,绳缆被缠绕在绕臂上实现纵向打捆。绕臂电机驱动绕臂携带纵向绳捆横向转动,配合排线器的引导将绳缆均匀缠绕在纵向绳捆上实现横向打捆。利用生头气动机械手完成绳缆的剪断和生头。打捆机横向打捆时,排线器则引导绳缆移动,保证横向绳捆匝与匝间均匀紧密。绕臂横向打捆转速范围为0~150 r/min,绕臂的存在和打捆工艺的需求使绕臂电机运转具有大惯量、低转速、频繁启停的特点,从而导致绕臂电机失步风险上升,因此需要控制精度更高、可靠性更好的控制算法,图2为横向打捆原理示意图。
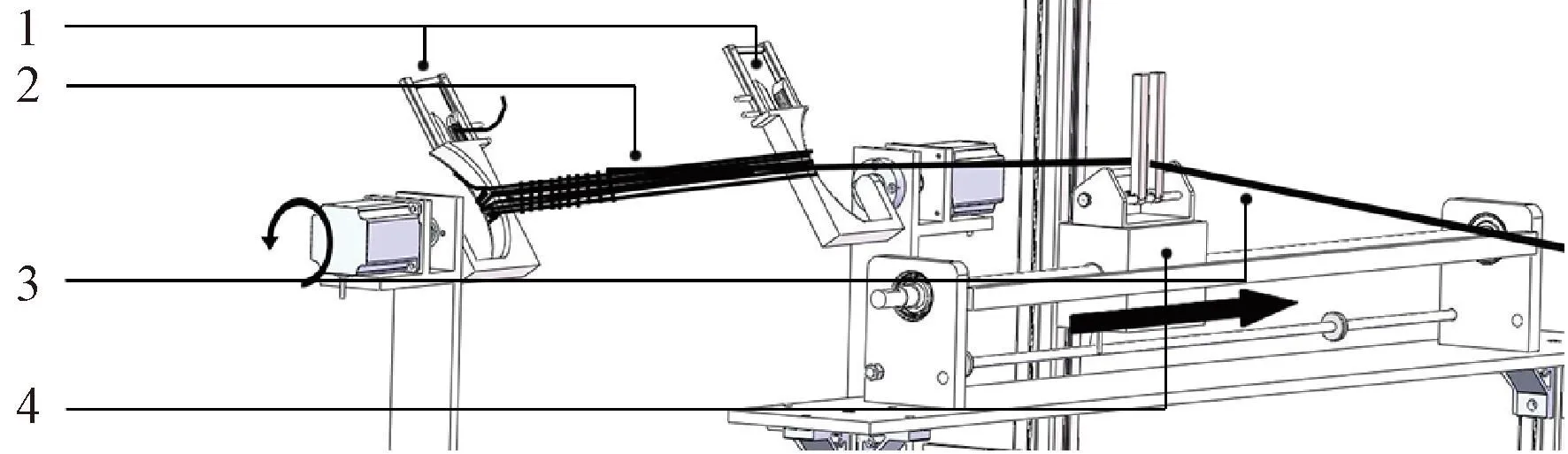
注:1-绕臂;2-绳捆;3-绳缆;4-排线器。图2 横向打捆原理示意图Fig.2 Schematic diagram of horizontal bundling
2 小径短绳自动打捆机绕臂电机PID控制
2.1 绕臂电机数学模型
步进电机是广泛应用于高精度开环控制系统和低速开环控制系统的数字控制电机[4],随着对步进电机精度要求的提高,近几年针对步进电机的闭环控制的研究进展迅速。步进电机低频工况下输出转矩较大、控制简单、成本低,很适合用作小径短绳自动打捆机绕臂电机。
步进电机相线圈绕组反电动势[5]为
UA=ωkmsin(Zrθ)
(1)
UB=ωkmcos(Zrθ)
(2)
式中:UA、UB分别为步进电机A相和B相的线圈绕组反电动势;ω为转子角速度;Zr为转子齿数;km为步进电机反电势系数;θ为转子机械转角。
由式(1)和式(2)计算得到相电流方程:
(3)
(4)
式中:L为A、B相线圈绕组的自感;VA和VB分别为电机A、B相线圈绕组电压;iA和iB分别为电机A、B相线圈绕组电流;R为电机A、B相线圈绕组电阻。
步进电机A、B相线圈绕组的电磁转矩分量方程TA、TB分别为
TA=iAkmsin(Zrθ)
(5)
TB=iBkmcos(Zrθ)
(6)
步进电机瞬态电磁转矩由两相转矩求和得到,根据式(5)和式(6)计算得到得步进电机的瞬态电磁转矩:
Te=iAkmsin(Zrθ)+iBkmcos(Zrθ)
(7)
由运动学方程得电机电磁转矩与负载之间关系为
(8)
式中:J为电机转子和绕臂的总转动惯量;B为速度比例系数;TL为负载转矩。
将式(7)代入式(8)计算得运动方程为
(9)
为简化模型,采用单相励磁,绕臂无外部负载,在任何一时刻单相励磁的步进电机只有一相励磁,电机运动方程为
(10)
增量运动方程为
(11)
式中:δθ=θ0-θi为步进电机在i时间段内转角的增量,δθ很小,对其线性化处理[6]后得
(12)
对式(12)进行拉氏变换[7],并代入初始值0得
(13)
所用绕臂电机型号为富兴HSTM 57-1.8-S-76-4-2.8,电机参数如表1所示。

表1 HSTM 57-1.8-S-76-4-2.8电机参数
由式(13)得传递函数为
(14)
2.2 经典遗传算法和经典自适应遗传算法的缺陷
遗传算法是Holland[8]在Mendel的遗传学和Darwin进化论基础上提出的并行随机搜索优化算法。该算法将待优化参数编码成群体中的个体,按照适应度函数评判每个个体的适应度并以此获得本代种群的适应值排名,根据Darwin进化论中“适者生存”的原则进化,每次进化中按照Mendel遗传学中“选择、交叉、变异”的原理进行个体间的繁殖进化,经过不断重复进化,适应值高的“优良基因”被保留下来,适应值低的“基因”被淘汰。由于绕臂电机运转具有大惯量、低转速、频繁启停的特点,绕臂电机失步风险增大,步进电机常用的闭环控制方法难以保证控制精度,为此采用遗传算法对PID调参以控制绕臂步进电机。
交叉率的选择对遗传算法的求解结果影响很大[9]。经典遗传算法设计之初未考虑到算法有收敛速度慢、局部最优解和求解精度低的问题,未对遗传算法交叉率深入研究,交叉率为0.80~0.95的常数。
经典自适应遗传算法以个体适应值为个体分配交叉率[7],其交叉率函数为
(15)
式中:Pc为个体交叉率;fmax为种群最大适应值;fp为种群平均适应值;f为两交叉个体较大适应值。
经典遗传算法使用的交叉率是恒定值,对不同个体采用统一的遗传策略,导致进化过程中出现的优秀基因在后续的进化中可能出现退化现象,且求解精度低、收敛速度慢。自适应遗传算法解决了经典遗传算法优良基因退化的问题。采用自适应交叉率根据个体适应度排名进行自适应遗传操作时:适应度高的优良基因个体交叉率较低,有较大概率不经交叉直接遗传到下一代;适应度低的个体交叉率较高,劣等基因有较大概率发生变化后遗传到下一代。但经典自适应遗传算法进化前期,群体中的优良个体通常为局部最优解,这使局部最优基因大量遗传到后代,增加了寻找全局最优解的难度,且容易陷入局部最优。
3 改进自适应遗传算法PID控制
3.1 自适应遗传算法PID控制

(16)
式中:KP为比例系数;KI为积分系数;KD为微分系数。
图3为遗传算法PID参数整定流程图。

图3 遗传算法PID参数整定流程图Fig.3 Genetic algorithm PID parameter tuning flow chart
由图3可知,遗传算法PID参数整定分为5步:
1)确定KP、KI、KD参数范围。算法在此范围内寻优,参数范围的选取决定了寻优速度和寻优精度。
2)选取初始种群。初始种群在参数范围随机产生,每个个体都是一个潜在解,个体基因以浮点数形式编码,编码长度决定了寻优对象个数[11]。本文对KP、KI、KD等参数寻优,故编码长度为3。图4为PID参数编码示意图,图中3个浮点数分别代表参数KP、KI、KD。

图4 PID参数编码示意图Fig.4 PID parameter coding diagram
3)确定适配函数并计算适应值。判断是否到达规定进化代数,若没到达进化代数则进行遗传操作,若到达进化代数则解码输出。
4)遗传操作。根据个体适应值用适应度比例法选择被复制到交叉仓的个体,高适应值个体在交叉仓中有多个副本,低适应值个体在交叉仓中没有副本或者副本较少,根据交叉率和变异率对交叉仓中个体基因进行交叉变异。
5)解码输出结果。由于本文使用浮点形式直接对KP、KI、KD编码,解码过程直接使用染色体即可。
遗传操作主要包括复制、交叉和变异,个体装入交叉仓操作为复制操作,复制操作根据个体适应值用适应度比例法决定个体被复制到交叉仓个数。交叉操作是对复制操作选入交叉仓的个体进行的相邻两个体间的基因段交换,本文选择单点交叉,交叉点随机选择。交叉后的种群根据个体变异率随机对基因上某一点变异,经过变异后得出的种群就是下一代种群。
3.2 目标函数确定

(17)
式中:J为目标函数值;e(t)为误差;u(t)为输入量;tu为上升时间。
目标函数值反映了个体适应值水平,目标函数值越小,个体适应值越大,即个体越优秀。
3.3 自适应交叉率和自适应变异率
经典遗传算法中交叉率和变异率是恒定不变的常数,不可避免地把优良基因按照与劣等基因一样的概率交叉和变异,这会导致优良基因退化。为避免盲目交叉和变异,减小优良基因在交叉和变异中变为劣等基因而导致退化的概率,在遗传进化中要让适应值高的优良基因有较高概率直接遗传到下一代,对适应值低的劣等个体有较高概率发生基因变化后再遗传到下一代,由此可总结出对遗传算法的3个优化原则:
1)高适应值排名个体被复制到交叉仓的个数较多,低适应值个体被复制到交叉仓的个数较少或不被复制。
2)高适应值排名个体产生下一代时基因发生变化的概率降低,优良基因的退化率降低,劣等个体产生后代时基因发生变化的概率高,这让劣等基因有足够机会变化。基因发生变化的方式是交叉和变异,因此需要根据个体的适应值给不同个体分配不同的交叉率和变异率。
3)在进化代数较低的情况下,种群中高适应值个体有较大可能是局部最优解,这种情况下适应值排名较高的个体也应该具有较高的交叉率和变异率以冲出局部最优,但随着进化代数增加,种群平均适应度不断增大,种群中较高适应值的个体越来越接近全局最优解,此时降低高适应值排名的交叉率和变异率以保留真正的优秀基因。
黄金分割比是普遍存在于自然界的数学现象[12],本文用黄金分割比划分种群中的优良个体和劣等个体,以种群中适应值排名38.2%为临界点,适应值排名在临界点之前的为优良个体,适应值排名在临界点之后的为劣等个体,无论进化代数是多少,种群中后61.8%个体总为劣等个体。个体自适应交叉率和自适应变异率用以0.618为底的指数函数规律表征,劣等个体的个体交叉率和变异率用较大的常数加快劣等基因的变化,优良基因根据进化代数和适应值排名计算交叉率和变异率。应用黄金分割比构造改进遗传算法自适应交叉率和自适应变异率的函数,分别如式(18)和(19)所示。
(18)
(19)
式中:f为个体适应值;fb=fmin+0.618×(fmax-fmin)为黄金分割点适应值;fmax为种群最大适应值;fmin为种群最小适应值;G为当前种群进化代数。
图5为改进自适应遗传算法交叉率示意图。由图5可知:从个体适应值排名来看,适应值排名低于黄金分割点(f≤fb)的劣等个体拥有较高交叉率促进个体进化,增加劣等基因进化为优良基因的概率,个体适应值排名高于黄金分割点(f>fb)的优良个体随适应值排名的升高逐步降低交叉率;从进化代数来看,进化代数很低时,群体中高适应值排名个体很可能是局部最优解,因此低进化代数群体中高适应值排名个体有较高交叉率,当进化代数较高时,种群的整体适应值水平升高,此时种群中高适应值排名个体离全局最优解越来越近,高适应值排名个体的交叉率逐渐降低以抑制退化。上文中的“个体”在本研究中为PID参数组(KP、KI、KD),“高适应值排名个体”指使步进电机具有更好控制效果的PID参数组。

图5 改进自适应遗传算法交叉率曲线Fig.5 Improved adaptive genetic algorithm crossover rate curve
4 改进自适应遗传PID仿真与试验验证
本算法采用种群数量为30个,进化代数为600代,采用浮点数编码,目标速度为150 r/min,根据常规Z-N整定法[13]确定PID控制器的KP为15~30,KI为15~30,KD为0~1,图6为改进自适应遗传PID算法和经典遗传算法目标函数值曲线,BestJ为每代种群中最优个体目标函数值,BestJ越低,适应值越高,控制效果越好。
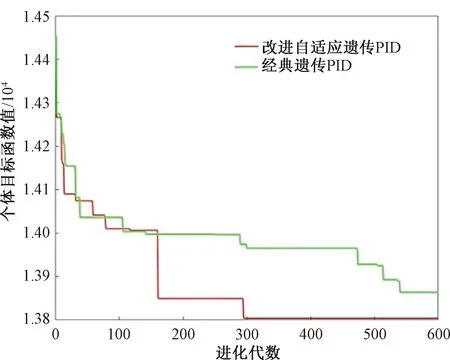
图6 目标函数值曲线Fig.6 Objective function value curve
由图6可知:改进自适应遗传PID在进化300代时便收敛到全局最优解,经典遗传PID在收敛到600代时仍未收敛到最优解。改进自适应遗传PID相比经典遗传PID算法,收敛速度加快了50%,且求解精度更高。
图7为用改进自适应遗传PID算法和经典遗传PID算法以150 r/min为目标值的仿真结果。由图7可知,改进自适应遗传PID在0.15 s附近到达目标值,经典遗传PID在0.175 s附近到达目标值,且改进自适应遗传PID到达目标值后超调量更小。
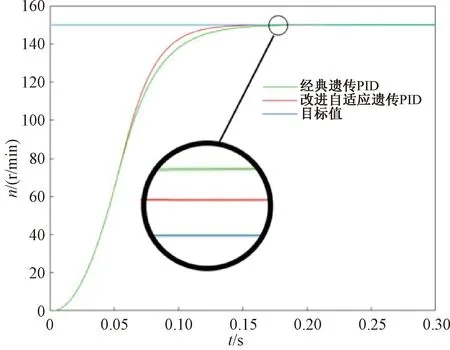
图7 算法仿真结果Fig.7 Algorithm simulation results
绕臂电机驱动绕臂进行横向打捆,牵引绳缆进入绳捆,在横向打捆时对绕臂电机分别使用改进自适应遗传PID算法和经典遗传PID算法进行控制,并将控制器捕捉到的绕臂转速上传到PC端,用VOFA+软件呈现,可以根据软件输出的速度图得出算法控制效果。
本文用STM32 F103ZET6型作为步进电机控制器,用TB6600型驱动芯片作为步进电机驱动器,以150 r/min为目标速度,对绕臂电机分别用改进自适应遗传PID和经典遗传PID控制。图8为编码器采集回传的绕臂电机速度图。由于TB6600驱动芯片的驱动精度、抑制振动和减少发热等方面的性能较差,芯片在运行阶段有微小的速度波动。
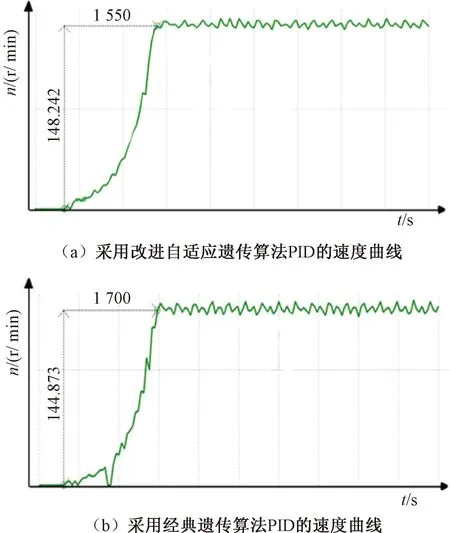
图8 速度曲线图Fig.8 Speed curve verification chart
改进算法和经典算法的控制效果对比如表2所示。由表2可知,改进自适应遗传PID算法控制下的打捆机绕臂速度相比经典遗传PID稳态误差降低了30%,响应时间提高了9%,在启动阶段速度波动更小,对价格低廉、控制简单的步进电机的性能有了一定提升。

表2 控制效果比较Table 2 Comparison of control effect
5 结 论
1)在遗传算法中引入进化代数和适应值排名对遗传操作的指导作用,避免了经典遗传算法进化中优良基因的退化问题和经典自适应遗传算法容易陷入局部最优的问题,使用改进自适应遗传算法PID降低了打捆机绕臂步进电机的稳态误差、提高了响应时间、减小了振动,使打捆精度、打捆效率和绳捆均匀度明显提高。
2)基于MATLAB软件的仿真结果表明:改进自适应遗传PID相比经典遗传PID有更快的收敛速度、更高的求解精度。
3)试验验证结果表明:改进自适应遗传PID相比经典遗传PID降低了稳态误差、加快了响应速度、削弱了电机运行的振动和噪声。
