超声焊接全状态频率跟踪算法∗

姚 震 罗子伦 刘凯捷 丁荣杰 莫毅强 何 建 乌斯别斯基·亚历山大

(1 广东工业大学 广州 510006)

(2 广州市科普超声电子技术有限公司 广州 510520)

(3 白俄罗斯国家科学院国际技术转移中心 明斯克 220012)

0 引言

超声焊接被应用于动力电池的极耳及线束焊接生产中，其焊接质量直接影响产品的整体性能、良品率和使用寿命[1]。动力电池极耳超声波金属焊接频率通常为20 kHz，焊接功率达数千瓦，焊接过程负载变化剧烈且焊接时间短[2]，需要更快的频率跟踪速度。当换能器失谐时，焊头的输出功率波动较大，容易出现虚焊或过焊等现象[3]。超声换能器失谐工作时无功功率增加，换能器的电流电压升高，导致频率进一步漂移，容易损坏换能器。

换能器焊接失谐一般指工作在无阻性点状态或频率误跟踪。超声焊接系统为非线性时变系统，其传递函数建模过程复杂。数字超声电源往往采用变步长跟踪[4]、PID[5]、模糊PID[6]算法等，不需建立具体模型的算法，优点是控制易实现，满足一般情况下的工况。但也存在一些缺点，PID 参数整定困难，出现误跟踪无法自动复位，在无阻性点状态时容易频率大幅波动。

本文基于梅森等效电路，通过数学公式推导，提出了一种全状态的频率跟踪算法，能在有阻性点时选择谐振频率或反谐振频率作为追频目标；在无阻性点时工作在换能器电压电流最小相位差频率下。新算法能同时计算出谐振频率与反谐振频率的值，判断换能器是否存在阻性点，并能实现误跟踪的自复位。

1 换能器无阻性点状态与频率误跟踪

超声换能器主要完成电能转换为机械能的过程，通常采用机电等效法对其工作过程进行分析。图1 为压电换能器的梅森等效模型(忽略介电损耗)。

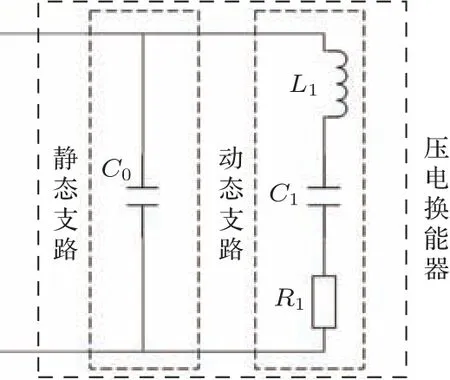
图1 压电换能器等效电路图Fig.1 Equivalent circuit of the piezoelectric transducer

在图1 中，L1为换能器的动态电感，表征其等效质量；R1为换能器的动态电阻，表征其机械内阻；C1为换能器的动态电容，表征其柔度[7]。三者串联的支路为换能器的动态支路。C0为换能器的静态电容，是换能器的夹持电容，C0所在的支路为换能器的静态支路。换能器的复阻抗Z和发波角频率ω之间的关系为

式(1)中，角频率ω=2πf，f为换能器的驱动频率。

一般情况下，Z(ω)=0 存在两个解，分别是谐振频率fr和反谐振频率fa。在焊接过程，这两个频率随时间不断变化，而频率跟踪则是在这两个频率点中选择一个作为跟踪目标，使换能器始终在谐振状态工作，保证焊接效果。

1.1 换能器的无阻性点状态

换能器的动态电阻R1主要受负载的影响，换能器的负载与焊接压力、模头纹路尺寸和被焊接的材料有关。通过式(1)可知：当R1满足式(2)时[8]，换能器处于无阻性点状态。

换能器的相位角与负载大小密切相关，图2 为不同负载下换能器相位曲线变化图，其中负载2 大于负载1。

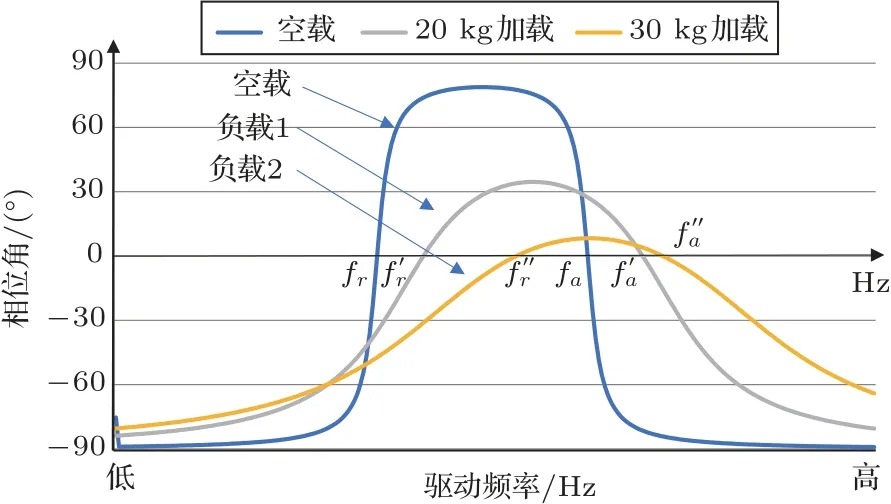
图2 不同负载下换能器相频特性曲线比较Fig.2 Relationship between the frequency and phase of the transducer in operation under different loads

由图2 可知，随着负载加重，换能器的fr和fa在逐渐靠近，换能器的感性区也在逐渐缩小，最终突破临界点后，换能器的阻性点消失。此时，无论以何种频率发波，换能器都无法在谐振状态工作。在无阻性点状态工作时，输出功率会存在无功功率。

1.2 频率的误跟踪原因分析

误跟踪是指追踪的频率点发生变化。图3 为换能器的相频特性曲线，依据换能器振动频率和阻抗特性的不同，整个曲线可分为4 个区域。设换能器的当前工作频率为f，当ffa为第四个区域，此时换能器阻抗呈现容性，当ω增加时，换能器容性会越来越强。传统的频率跟踪算法通过对起始跟踪频率所处区域来确定跟踪目标。当起始频率处于第一、第二区域时，跟踪目标为fr；当起始频率处于第三、第四区域时，跟踪目标为fa。在小负载的情况下，第二、第三区域比较宽，传统跟踪算法根据跟踪目标来设定不同的跟踪频率上下限，避免误跟踪的发生。

图3 换能器的相频特性曲线Fig.3 Schematics for the phase and frequency of the transducer

由式(1)可以推导出fr、fa两个频率的间距为

在超声金属焊接中，负载重且波动大，导致跟踪频率上下限难以合理设置。假设目标跟踪频率为fa，根据扫频结果，起始频率定位在第三、第四区域。焊接加载时，换能器的R1会随着负载增加而增加，连续的焊接会使换能器发热，导致换能器的C0上升。由式(3)可知，假设L1、C1不变，当C0、R1增加时，fr、fa的间距减小[8]，即第二、第三区域缩小。负载抖动和频率跟踪的延迟有可能导致电源的发波频率从第三区域跑到了第二区域，引发误跟踪(追fa变为追fr)。现有的变步长频率跟踪、PID、模糊PID 等各种频率跟踪控制算法，一旦发生误跟踪就难以找回目标跟踪频率。

图4(a)和图4(b)均为同次焊接时换能器电压电流波形，深蓝色线为换能器电压波形，浅绿色线为换能器电流波形。电源匹配电路为LC 匹配，跟踪算法为变步长频率跟踪算法[4]，在焊接的全过程换能器均处于谐振状态。图4(a)中为跟踪到反谐振频率点时的电压电流波形，换能器电压达1380 V，电流是663 mA。电压高电流低是换能器处于fa的特征，此时焊接功率为915 W。图4(b)中为跟踪到谐振频率点的电压电流波形，电压降为844 V，电流上升到1780 mA。电压低电流高是换能器处于fr的特征，此时焊接功率上升到1502 W，功率上升近65%。由此可知，换能器的跟踪频率由fa误跟踪到了fr，出现这种情况容易导致功率波动，影响焊接一致性。

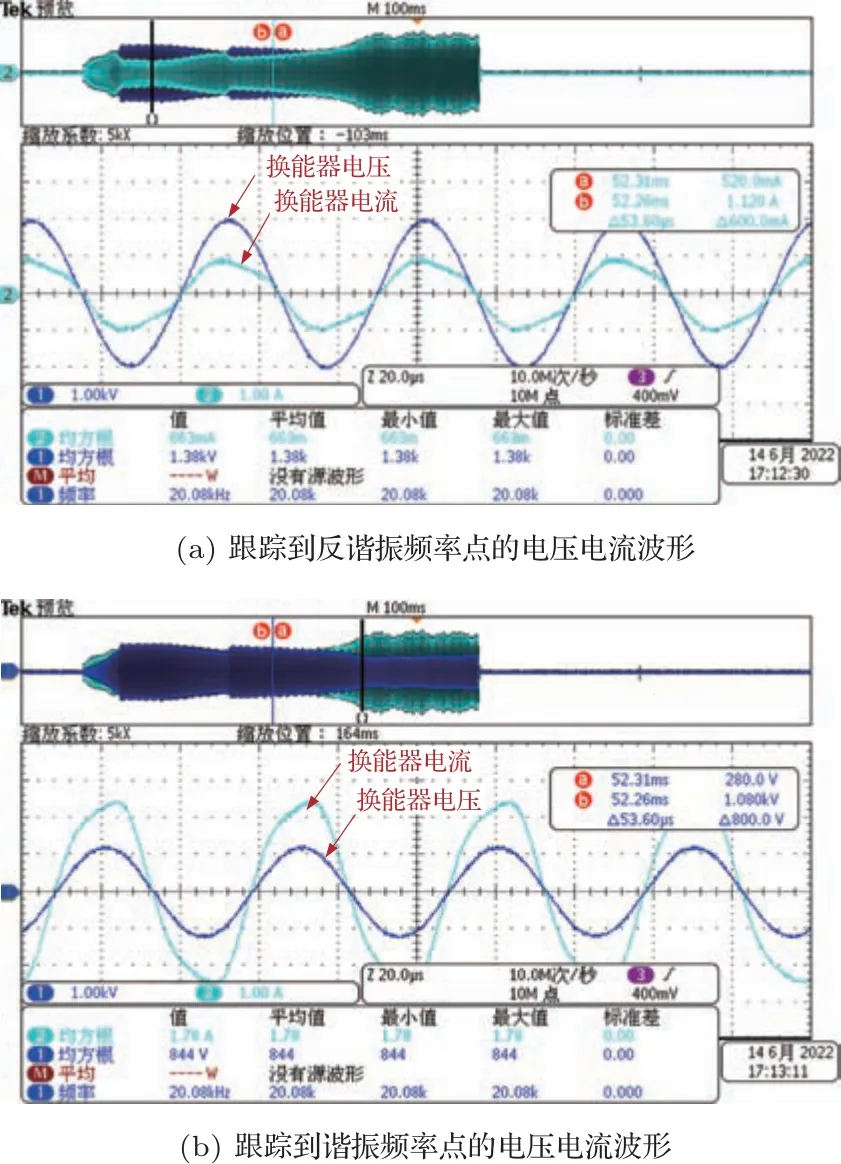
图4 金属焊接频率误跟踪换能器电压电流波形图Fig.4 Waveforms of the voltage and current applied on the transducer during the process of welding the metal when its frequency was tracked inaccurately

2 全状态频率跟踪算法的推导与实现

2.1 全状态频率跟踪算法的推导

假设当前电源输出频率为f，角频率为ω，其对应的换能器两端电压电流相位差为θ。由于相位差角度与负载阻抗角相同[4]，由式(1)可以推导出tanθ与ω之间的关系为

在式(4)的基础上进一步化简可以得到以下表达式：

为使表达式变得简洁，现进行以下等效变换：

把式(6)代入式(5)后等式两边同时乘ω，可得

不难看出，式(7)有4 个解，由于负频率没有物理意义，舍去两个负数解后可得

当阻性点不存在时，目标频率计算公式如下：

在式(7)和式(8)中，ω是当前的发波频率，tanθ则是换能器相位差的正切值，可选fa或fr作为目标跟踪频率。因此，只要求出K1、K2、K3三个未知数，即可同时得到换能器的谐振频率和反谐振频率。值得注意的是，当-4K1K3<0时，函数无实数解，说明换能器此时不存在阻性点，其计算方式如式(9)所示。

2.2 全状态频率跟踪算法的实现

依据fr和fa的计算公式(式(8))，可根据应用场合选择跟踪目标是fr还是fa，一般情况下fr用于中小负载的工况，而fa则用于负载较大的情况。以fa为跟踪目标为例，全状态频率算法流程图如图5所示。

图5 全状态频率跟踪算法流程图Fig.5 Algorithm flow for the transducer was generated at any frequency

每间隔一段时间采集相位差，实时计算出驱动频率。图5 中的f1为单次焊接的首个发波频率，同理fn则为第n次改变后的发波频率，其对应的换能器电压电流相位差为θn。流程图中还存在有两个控制参数，分别为抖动系数s和最大限定步长fmax。两个控制参数会共同影响算法的跟踪速度和稳态误差。

一般通过扫频获取换能器空载时的fa作为起始发波频率，并依照fn=fn-1+s·n%3 的方式得出算法起始所需的3 个f值和θ值。后续驱动频率根据本次和前两次发波的频率及其θ值进行计算得出，计算结果与上次输出的差值再与fmax比较，选择较低的输出。当θn小于阈值θl时，fn将在fa附近进行小范围波动。

2.3 抖动系数和最大限定步长对算法的影响

设置抖动系数和最大限度步长虽然影响算法跟踪速度和稳态误差，但增加了算法稳定性。从仿真中发现，当θ接近0 时，每一次的跟踪步长将会变得很小，就会导致计算的3 个发波频率非常接近，计算的目标频率会出现严重的跳变。另外运算器的精度及计算误差也会造成目标频率的跳变。抖动系数就是人为加入微小偏差，消除计算频率的跳变。通常换能器的R1是时变的，每次采样值与理想值之间存在误差，可通过最大限度步长来限制这种误差的影响范围。

3 仿真与实验验证

3.1 仿真设计

为了验证算法的可行性，本文采用仿真软件对全状态频率跟踪算法进行理论验证。仿真设计的需求为：(1) 换能器负载以连续的方式变化。(2) 反馈需要以离散的方式获得。(3) 结果则需要以曲线的方式较为直观地展现出来。选取20 kHz 超声焊接换能器，使用阻抗分析仪测试其等效参数，如表1所示。

表1 换能器等效参数Table 1 Equivalent parameters of transduce

忽略焊接时的抖动影响，换能器R1总体是以先快后慢的方式进行变化的[9]，为了更接近实际负载对换能器的影响，设置R1以式(10)方式变化，其中参数K可用于调节R1的变化速度。

仿真设计思路如下：

(1) 假设换能器符合梅森等效模型，其等效参数初始值如表1 所示。焊接开始后，换能器的R1随时间以式(10)规律变化。

(2) 设定超声电源的起始频率，每个控制周期输出一个目标值，此目标值为下一个控制周期电源的发波频率，把这个频率输入到模型中，根据当前的等效参数计算并返回换能器相位差θ值。

(3) 记录整个仿真过程中发波频率、fa和fr的值，将换能器相差角随时间的变化绘制成曲线，观察其在理想情况下，算法的跟踪速度、跟踪稳定性和跟踪精度。

3.2 仿真结果分析

仿真时算法的控制周期为100 µs，焊接时间选择0.05 s，所需要用到的反馈值tanθ则基于梅森等效电路通过理论计算获得，从而得到该发波频率下对应的θ值。仿真结果如图6∼8所示。

图6 以fr 为跟踪目标的仿真结果Fig.6 Simulation results with fr as the tracking target

图6 是以fr为跟踪目标时，换能器两端电压电流相位差、fr、fa和发波频率随时间的变化曲线。为了验证算法能在误跟踪时自复位，将跟踪的起始频率设置为20170 Hz (远离fr值，跨过fa值)。可以看出，发波频率在焊接开始后在5 ms 左右跟踪到fr，并在短暂的抖动后完全跟上。在之后的焊接时间里，跟踪稳定且几乎没有稳态误差，跟踪精度达0.1 Hz。

图7 是以fa为跟踪目标时，换能器两端电压电流相位差、fr、fa和发波频率随时间的变化曲线。这里把将跟踪的起始频率设置为19830 Hz (远离fa值，跨过fr值)。虽然发波频率也可以在焊接开始后5 ms 左右跟踪到fa，完成误跟踪的自恢复，但相对于跟踪目标为fr情况，其跟踪精度与跟踪速度均有下降，跟踪精度只有2 Hz。

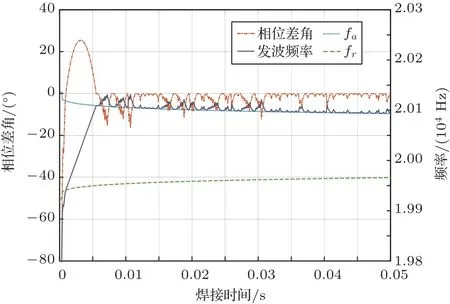
图7 以fa 为跟踪目标的仿真结果Fig.7 Simulation results with fa as the tracking target

图8 为换能器在无阻性点状态时，换能器两端电压电流相位差、fr、fa和发波频率随时间的变化曲线。在后半段，随着R1的增长换能器进入无阻性点状态，fr和fa合并成一条曲线，为换能器容性最低点频率的曲线。在换能器进入无阻性点状态后，算法自动更换控制目标，在短暂的抖动后完成频率跟踪。但是，相对于阻性点存在的情况，其跟踪精度有所下降，只有4 Hz。在R1很高的情况下，换能器的相位随频率变化的灵敏度会下降，在相位曲线上仍具有较高的稳定性。

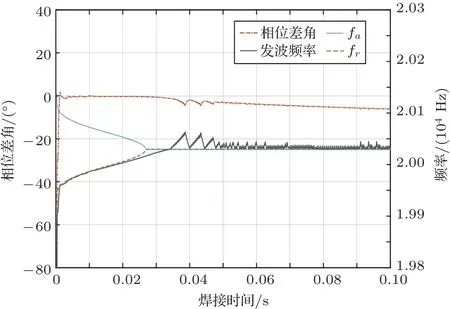
图8 无阻性点状态时算法跟踪仿真结果Fig.8 Algorithm tracking simulation results in the non-resistance point state

3.3 焊接实验验证

为了验证算法的实际效果，搭建实验平台进行验证。其中电源的控制芯片为TMS320F28377S，主电路采用LC匹配[10]，焊件为3层0.2 mm铜镀镍金属片，焊接功率约为1100 W。

实验中的电源驱动频率和相位差数据由超声电源通过串口导出，与TEKTRONIX 示波器MDO3104 测得数据一致。假定换能器电压电流相位差小于5°为谐振状态，则驱动频率不改变。以谐振频率fr为跟踪目标的结果如图9 所示，图9(a)为焊接时换能器两端电压电流波形图，图9(b)为驱动频率和相位差随焊接时间的变化曲线。跟踪的启动频率设置为20010 Hz，气压为0.2 MPa。

图9 以fr 为跟踪目标的实验结果Fig.9 The experimental result when the algorithm uses fr as tracking target

图10 是在跟踪目标为反谐振频率fa时的实验结果，其中图10(a)为焊接时换能器两端电压电流波形图，图10(b)为驱动频率和相位差随焊接时间的变化曲线。焊接工况与跟踪目标为fr时相同。为了验证算法的自复位效果，跟踪的启动频率同样设置为20010 Hz。

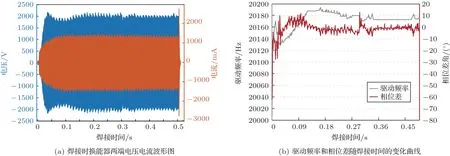
图10 以fa 为跟踪目标的实验结果Fig.10 The experimental result when the algorithm uses fa as tracking target

把焊接时的气压从0.2 MPa 提高到0.4 MPa，使得换能器处于无阻性点状态，测试算法在换能器处于无阻性点时是否能较为稳定的跟踪。图11 为换能器处于无阻性点状态时的频率跟踪效果，其中图11(a)为焊接时换能器两端电压电流波形图，图11(b)为电压发波频率和换能器的相位差随焊接时间的变化曲线。

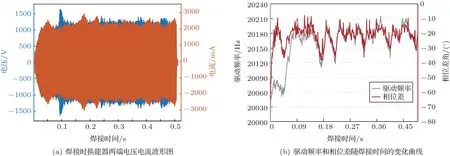
图11 无阻性点状态时算法跟踪实验结果Fig.11 The experimental results when the transducer is in the non-resistance point state

上述实验结果表明，算法能够较易实现谐振频率或反谐振频率的频率跟踪；在无阻性点状态时仍能维持较小相位差。存在阻性点时可完成负载动态变化(持续约80 ms)的跟踪，随后的相位差基本保持在8°以内，在换能器处于无阻性点时不会出现严重的频率失锁问题，跟踪效果稳定。

4 结论

本文主要研究超声焊接的频率跟踪技术，考虑了换能器的负载特性，提出全状态频率跟踪的算法。超声电源可以根据焊接对象选择工作在谐振或反谐振频率点。仿真结果和焊接实验均表明，算法能够避免误跟踪；启动阶段的起始频率与目标频率相差较大时，追频时间大约5 ms；在重载情况下，换能器谐振频率消失时，仍能够找到最佳工作频率稳定工作。本文提出的控制算法可应用于负载变化快的场合，也可为动力电池上连接件、线束等较厚工件的超声焊接提供参考。