细棒入水动力学特性的解析计算与数值模拟

张宇锋,谢 东,韦相忠,上官王佐

(1. 广西中医药大学 药学院及公管学院,广西 南宁 530200;2. 贵州电子信息职业技术学院,贵州 凯里 556000)

重物入水问题广泛存在于我们生活的各个领域之中,如水上飞机、海上溅落的工程器件、潜艇入水,鱼雷入水[1]等.在物体入水的过程中会伴随着一系列运动现象,比如当入水速度较快且物体入水有效面积足够大,在物体与水面接触碰撞的时候会在水面下产生空泡[2],影响物体的运动状态.

从试验上和理论上研究重物入水问题及其影响因素具有重要的实际应用价值[3].上世纪50年代前后,美国海军联合多家研究机构和高校等开展了大量的入水问题的基本研究.当时Duez等人[4]和Korkmaz及其合作者[5]分别对不同亲水性表面和不同亲水程度的球体和柱体进行了入水对照试验研究.Worthington从实验上对垂直入水的钢球所产生的入水空泡、喷溅的现象用闪光照相机来进行记录研究[6].进入21世纪以来重物入水问题仍然是一个被广泛研究的课题,例如苗圃等人对圆柱体高速入水做了数值模拟研究[7],安伟光、蒋运华等人研究了运动体高速入水非定常过程[8].

一般而言,物体入水会产生水下空泡从而影响物体的运动状态,因此入水问题常与水空泡的产生一起受大量研究者的广泛关注,例如最近侯宇、黄振贵等人的空心圆柱低速垂直入水试验研究[9], 施红辉等人研究了细长物体高速入水时产生的空泡对其速度变化的影响[10],杨柳等人研究了超弹性球体入水过程空泡演化及球体变形特性[11].

本文结合理论解析计算与数值模拟,研究了质量均匀分布的细棒从水面垂直低速入水这一典型物理过程,探讨了细棒入水初速度、水的阻力系数和细棒密度这几个主要因素对细棒入水后的运动状态的影响.此前已有多位学者研究了物体入水问题,并进行了数值计算与实验的研究讨论[12],但较少涉及对重物密度和水的阻力因素的讨论,包括理论上和实验上的.下面我们从这一物理模型出发,对细棒进行受力分析后根据牛顿第二运动定律建立细棒运动的动力学微分方程,并求得该方程的解析解,然后进行数值计算,并讨论入水过程中各个因素对其入水动力学特性的影响.

1 物理模型与动力学方程

如图1所示,现考虑一质量均匀分布的细棒,设其密度为ρ、长为l、横截面积为s、质量为m,从水面以初速度v0垂直入水.选取水平面为坐标原点,以重力方向为正方向建立坐标系.假设水的阻力系数为k,且阻力大小与物体运动速率成正比,即

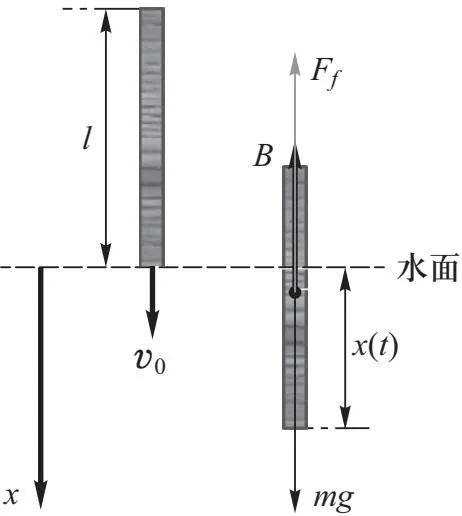
图1 物理模型

Ff=-kv

(1)

对其进行受力分析可知,细棒总共受到3个力的作用,即重力mg,浮力B,阻力Ff,其中重力mg为恒力,阻力正比于细棒的运动速率,而浮力B在细棒完全入水前为变力,随细棒的运动距离x(t)变化而变化.当细棒完全入水后,浮力B变为恒力.因此我们需要进行两种情况的讨论.即细棒完全入水前和完全入水后.

1.1 细棒完全入水前

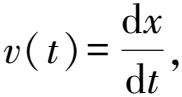
(2)

式(2)为二阶非齐次微分方程,其特征方程为

mr2+kr+ρ′sg=0

(3)

定义参数Δ:

Δ2≡k2-4mρ′sg

(4)

当Δ≠0时,r1≠r2.式(2)的解为

(5)

这里c1、c2为积分常数.根据速度的定义式,由式(5)对时间求导一次可得细棒的速度为

(6)

根据初始条件,当t=0时,初始距离为0,初始速度为v0,即x(0)=0,v(0)=v0,联立式(5)和(6),求得积分常数为

(7)

(8)

积分常数c1、c2代入式(5)得

(9)

此即细棒的位置函数.由式(9)对时间求导一次可得细棒完全入水前的速度函数:

(10)

需要注意的是,位置函数式(9)和速度函数式(10)仅适用于0≤x≤l.,即细棒完全入水之前.假设细棒完全入水的时刻为t0,理论上t0可以从式(9)求解得到,即

x(t0)=l

(11)

但该方程非常复杂无法得到精确解析解.在下一节,本文将用数值求解的方法求得近似解.

1.2 细棒完全入水后

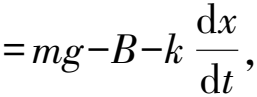
(12)

式(12)的解为

(13)

其中c3、c4为积分常数,而t0为细棒刚刚完全入水的时刻,由式(11)定义.注意,式(13)所给出的位置函数的适用范围为x≥l.

由式(13)对时间求导一次可得细棒的速度函数为

(14)

根据初始条件t=t0时,x=l,v=vt0,这里vt0为细棒刚刚完全入水时的速度,可以确定

(15)

(16)

至此,求得了细棒完全入水前后的位置函数x(t),即式(9)和(13),以及速度函数v(t),即式(10)和(14).

2 数值模拟与结果分析

现在根据在上节我们所求得的细棒入水动力学方程的解析解,进行数值计算,从而分析细棒在水中的动力学特性.不失一般性,设细棒长度l=2 m,横截面积s=1 cm2.我们考察不同的细棒密度和水的阻力系数,以及不同入水初速度,对细棒运动状态的影响.预先说明:为了避免重复书写简练,本文此后所有物理量数字,如果没有专门注明(除非特别标出其单位),均默认为国际单位制单位,比如速度单位为m/s,加速度单位为m/s2.

图2所示为水的阻力系数为k=1的结果,其中所有较粗的线为入水初速度不为零的结果,而所有稍细的线为入水初速度为零的结果.为简单起见,对非零初速度入水的,设所有不同密度的细棒均为v0=4 m/s,如图2所示.另外,同种类型的线都属于相同密度的细棒.

图2 不同密度和入水初速度的细棒入水后的速度演化

从图2可以看到,所有曲线的一个明显的共同特征是,当时间足够长后,同种类型(即细棒密度相同的2条)的曲线都趋向于相同的饱和值(渐进值).这个饱和值就是细棒的终极沉降速度.当细棒密度比水大时,即ρ>ρ′,细棒完全没入水后经过足够长的时间以后,随着细棒的速度不断增加,但增加的速率逐渐变小,细棒的阻力达到了最大值,最终阻力与浮力之和与其重力达到动态平衡,此时其合外力为零,故加速度为零,速度不再继续增加.这个速度的极限值,可以由细棒入水后的动力学微分方程(12)求出:令该方程等式左边的二阶导数项为零,即其加速度为零,可得kvmax=mg-lρ′sg,由此可得

(17)

另一方面,在式(14)中如果令t→∞,则该方程等式右边第一项趋向于零,也可得到同样的结果,因为细棒质量m=ρls.以图2中对应ρ=4 000的那条划线为例子,根据上述计算结果其极限速度应该为

vmax=(4 000-1 000)×2×0.000 1×9.8/1=5.88

这与图2所示结果是吻合的.相比各条曲线,可以看到当细棒密度比较大时,达到饱和速度的所需时间比较长,因为相应地其重力比较大,达到动态平衡所需的时间就比较长.由图2可见,这个极限速度,是不依赖于细棒的入水初速度的,即不管入水初速度是否为零.这个结果也可以从上述分析vmax的达到过程或者式(17)可以看到,vmax是不依赖于v0的.这个结论具有现实的物理意义,它适用于一般阻力系数可以近似为常数的沉降过程,如空中雨滴的下落的,跳伞者在空中的下落,重物在水中的沉降,等等.

然而,以非零初速度入水,较之于细棒由静止开始从水面释放入水(即初速度为0),从图2可以看到,细棒入水后最初的一段时间内其运动状态是不一样的.为方便起见,对不同密度的细棒,我们都赋予相同的初速度,即v0=4 m/s.如果细棒的入水初速度v0vmax,那么细棒入水所受到的阻力占比就较大,使得其入水后急剧减速最终降低到vmax,表现为v(t)曲线的斜率变大而快速下降.初速度v0比vmax大得越多,入水后减速越急剧,在图上表现为下降越陡峭.这个结果是很容易理解的,比如跳水运动员入水后,其向下的运动速度迅速减小继而开始向上浮出水面.当物体入水初速度非常大而其横截面积不是足够小,物体入水后将会激起大量水泡,从而极大地影响其动力学特征而使其变得极其复杂,这正是大量文献致力于研究的重物入水过程空泡演化问题[13].在这种情况下,本文所采用的模型,即入水物体所受到水的阻力与其速度大小成正比这一前提条件,也就是阻力Ff=-kv这条方程,将不再成立.由于本文所研究的入水物体为细棒,其横截面积足够小,且其入水初速度不是太大,入水空泡问题可以忽略.

如果细棒的密度不大于水的密度(即小于或等于水的密度),如图2中底部ρ=1 000,ρ=500 2组(4条)曲线所示,其极限速度为0,表明细棒最终会静止地悬浮于水中(这里我们暂且不进一步讨论此后细棒是否会从立着的状态翻转而最终横着悬/漂浮于水中,因为这是后续的问题不在本文讨论范围之内).为了验证这个结果,我们考察细棒的x(t)变化曲线.图3所示为细棒的x(t)曲线图.可以看到,绿色所示的为ρ=1 000的情形,其极限位置趋向于2 m,表明细棒恰好完全浸入水中,而红色所示的为ρ=500的情形,其极限位置小于2 m(实际数值为1.0 m),意味着细棒没有完全没入水中,而是悬浮于水中.其它3条曲线均为细棒密度比水的密度大的情形,因而细棒不断下沉而其位置随时间推移不断增大.这些曲线的斜率给出了各个对应情况下的细棒速率v(t),也就是图2所示的内容.为了能够更好地观察细棒密度不大于水的那2条曲线,该图的纵坐标取值范围的上限已经从50调整到了12,而图3内嵌的小图,则给出了缩小了的全局画面.同样地,所有较细的线代表入水初速度为零的,而较粗的线代表初速度为非零的情形.从图3可见,所有非零初速度入水的,其v(t)均在零初速度入水的v(t)之上,因为非零初速度的相比之下在相同时间内位移更大,这也可以从图2各组相同类型的曲线跟横轴所围面积大小的比较看出,这个面积就是位移.

图3 不同密度的细棒入水后的位置函数

(18)

推导上式过程中已经结合式(4)进行了简化.完全入水后则为

(19)

其中vt0为细棒刚刚全部没入水中瞬间(此刻时间为t0)的速度.

图4给出了根据式(18)和(19)而计算a(t)得出的数值结果.首先来观察实线那一组曲线,即细棒初速度为零的情况.当细棒从水面由静止刚刚被释放的那个瞬间,其合外力最大,为mg,即为细棒自身重量,所以此刻的加速度为a=mg/m=g,这个结果适用于全部不同密度的细棒,与ρ无关.这个结论与图4给出的数值结果是吻合的:这组实线都开始于同一点,(0, 9.8),然后快速下降.另一方面,也可以从细棒完全入水前的加速度方程式(18),结合Δ的定义式(4),简化之后可得到细棒初始时刻的加速度为

(20)

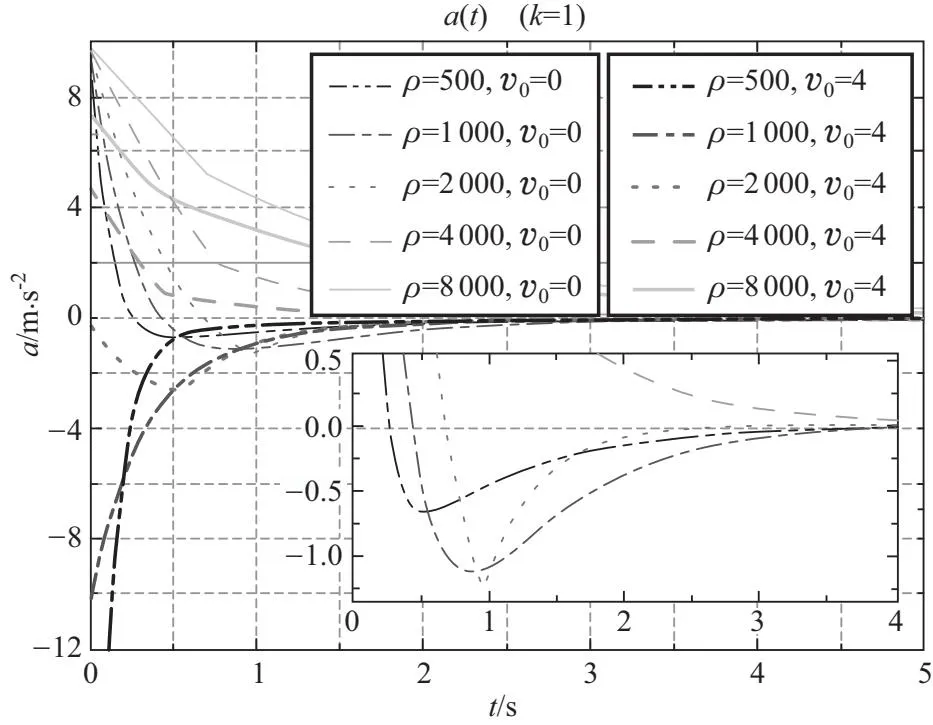
图4 细棒加速度变化曲线

令上式中v0=0可得a(0)=g,可见当细棒零初速度入水时,其初始加速度都是g,与密度无关.

但如果细棒以一非零初速度入水,则情况有所不同.从图4可以看到,a(t)曲线的初始点都逐个离开了点(0,9.8),而细棒的密度越小,偏离越大.这是因为从细棒刚刚入水那一刻开始,水的阻力开始作用于细棒,方向向上,与其重力方向相反.在数值计算中,我们都赋予不同密度的细棒以相同的初速度,v0=4 m/s.这意味着所有密度不同的细棒在刚刚入水后的那一刻受到水的阻力的大小都是一样的,但重力却各不相同,密度小的则重力较小,因而水的阻力在其所有外力中占比就较大,特别对于密度较小的细棒.比如ρ=500,1 000这两种情形,水的阻力远大于其重力,入水后使得其合外力向上且与其速度方向相反,从而使其加速度为负数,表现在a(t)曲线发端于纵轴负半轴非常下方处,如图4 中的对应ρ=500,1 000两条较粗的线所示.这种情形跟上述提到的高台跳水运动员入水,或者鱼雷入水等高速运动物体入水后的动力学特征相似.除了上述定性的分析,类似地也可以根据式(19)定量而精确地算出其初始时刻的加速度.以ρ=1 000为例:其质量为m=ρls=0.2,由式(20)算得其初始时刻的加速度为

a(0)=9.8-1×4/0.2=-10.2

与图4所示一致;而对ρ=500,其初始加速度a(0)达到惊人的-30.2,即大小达3倍重力加速度以上.

根据上述分析我们看到水的阻力在细棒的入水运动过程中对其动力学特性起到很大作用,而水的阻力是由入水物体的速度和水的阻力系数决定,即Ff=-kv.前面我们已经分析了物体运动速度,尤其是不同初速度入水,对其动力学特性的影响,下面我们考察水的阻力系数的影响.图5所示为水的阻力系数k=3的情形,其他参数与图2相同.在图2中,在v0=0的入水情形中当ρ=4 000时的v(t)曲线中并没有峰值出现,但在图5中,则出现了一个较小但足以辨认的峰值.这点可以从k=3的a(t)曲线中看出,如图6所示.可以看到,在t=0.4左右,加速度已经从正值跨过零轴变成负值了,不过负值幅度并不大,这恰好表现在图5中ρ=4 000所对应的蓝绿色线中那个小小的峰值.与图2具有共同特征的是,图5中各条v(t)曲线都趋向于各自的饱和值,不管入水初速度是否为零;而对相同的细棒密度,不同初速度入水后最终还是趋向于同一个速度饱和值,但它们趋向于饱和值的时间与图2中各条相应曲线有所不同,而饱和值则相应成比例地减少,因为此时水的阻力系数比图2中的要大3倍,因为速度饱和值同样地由vmax=(ρ-ρ′)lsg/k决定.

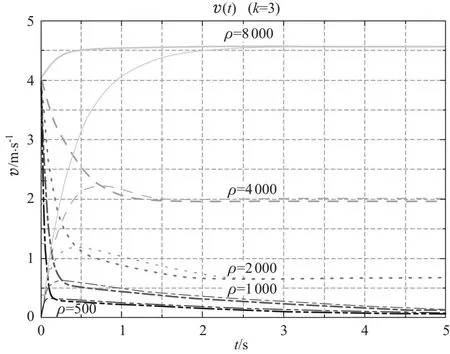
图5 几种不同密度的细棒入水后速度随时间变化

图6 细棒加速度变化曲线

类似于图2中对速度曲线的分析方法,我们也计算了k=3情形下的a(t)曲线,如图6所示.相比于图4,现ρ=4 000的划线也下破零轴,只有ρ=8 000的实线还仍然保持在零轴之上(参见图6内嵌图).从图6中可以看到,ρ=500的双点划线只是稍稍下破零轴(参加内嵌放大图),但幅度不大,表明向上的合外力幅值很小,对应于图5中ρ=500的双点划线中的那个小峰值.对比图5和图6,可以看到,加速度下破零轴的幅度越大,则对应图5中v(t)的峰值越明显.

从图5可以看到,相比于k=1(图2)的情形,在零初速度入水的情况下,虽然当细棒密度大于水时其下降速度较快地趋向于饱和值,但当细棒密度不大于水的密度时,反而比k=1时更慢地趋向于饱和值,如图5中最下面两条较细的曲线所示(即ρ=1 000,500的曲线).造成这种反差现象的原因是,当水的阻力系数较大(即k=3时)而细棒的密度不大于水的密度时,细棒刚开始入水不久速度还不大时,水的阻力和浮力就已经超过了其重力而使得其合外力改变方向朝上,于是细棒便开始减速.但此时离细棒的平衡位置还有一段距离,但合外力很小(参加图6内嵌图中对应ρ=1 000,500的两条曲线),所以细棒比较缓慢地减速下沉而逼近其平衡位置,从而最终静止地悬浮于水里,因而反而需要更长的时间才能到达极限速度,即零速度或静止.

为了比较不同的k值和ρ值对细棒的入水后的加速度的影响,在图7中我们给出了一组简单的对比.我们只考虑零初速度入水,因为如上述,非零初速度入水的效果相当于把a(t)曲线的端点往下拉再逐渐回归到零轴.为了能看得更清楚,我们只画出了k=1,3和ρ=2 000,4 000两两组合共4种情况.对于相同密度的细棒,更大k值的意味着入水后受到更大的阻力而总的合外力越小,因此较大k值的a(t)曲线在下方,而较小k值的a(t)曲线在上方,即较大k值的在较小k值的之下,这与图7所示吻合.类似地,在相同的阻力系数下,密度更大的在相同的位置x(t)下则向下的重力更大,因而向下的合力更大.因此,较大ρ值的a(t)曲线在上方,而较小ρ值的a(t)曲线在下方,这与图7所示也是吻合的.

图7 不同值k和ρ值下的加速度曲线

3 结论

综上所述,采用理论解析推导与数值模拟相结合的方法本文研究了质量均匀分布的细棒低速入水问题,分析了水的阻力系数和细棒密度这两个最重要的因素对其入水过程的动力学特性的影响.首先我们根据牛顿第二定律建立动力学微分方程并求得了解析解,由此进行数值计算并对细棒运动状态的动力学特性进行了详尽的分析.结果表明如果细棒的密度比水的大,细棒下沉过程中最终都会趋向于一个稳定的极限下沉速度,不管其入水初速度多少,该极限速度正比于细棒与水的密度差,反比于水的阻力系数;而密度差越大,从入水开始达到极限下沉速度所需时间越长.但当密度差较小时,细棒的下沉速度先达到一个峰值,然后减速并逐渐趋向于稳定极限下沉速度.根据对其受力分析和及其加速度变化的分析,速度峰值形成的原因得到了合理的解释.相反,如果细棒的密度不大于水的密度,则细棒入水后最终会静止不动而悬浮于水中,不管入手初速度多少.进一步的计算结果还显示,水的阻力系数越小,细棒达到极限下沉速度的时间也越长,反之则越短.

相比于由静止从水面释放入水,以非零初速度入水的效果相当于在细棒入水后的最初一段时间内增加了其阻力而改变了其所有合外力中各个力的对比,从而改变了细棒入水后的动力学特性,尤其是入水后的最初一段时间内;离入水时刻时间间隔越短,差异或效果越显著.但当细棒入水时间足够长后,无论其入水初速度是否为零,其运动状态终将趋于一致而无差别.