调压井底孔对水轮机调节系统过渡过程的影响
2024-02-28杜玉宝周同旭王柏柏孔昭年
杜玉宝,杨 旭,周同旭,王柏柏,孔昭年
(1.国投电力控股股份有限公司,北京 100034;2.中水北方勘测设计研究院有限责任公司,天津 300222;3.天津电气科学研究院有限公司,天津 300186;4.中国水利水电科学研究院,北京 100038)
1 研究背景
我国水电站调压井的设计计算长期以来借鉴国外的有关经验,原苏联制定的水电站设计规范中规定调压井的设置标准应满足:当电站独立运行或大于系统总容量50%的电站,建议K=16~20;装机容量只占系统容量10%~20%电站,建议K≥50;法国及日本设置调压井的条件为∑LiVi/Hr≥45换算成通用的术语即:Tw≥1.6~4.5 s;我国有关规程建议[1,2]:电站水流惯性时间Tw≥2~4 s为设置调压井的判据。在有关标准附件的条文说明中写道:“水电站是否需要设置调压室,最终要依据压力水道布置及水道沿线的地形、地质条件,机组运行条件机组调保参数的限制值,及机组运行稳定性和调节品质等由水电站水力机械过渡过程分析计算,并通过技术经济综合比较最后确定”。“为保证工程安全大、中型水电站施工设计阶段应根据主机厂家提供的机组参数采取数值模拟的方法进行机组调节保证计算、运行稳定性和调节品质分析,复核是否设置调压室”。显然,调压井仍然是水电站建设的重要工程措施,带调压井的水轮机调节系统过渡过程计算变得日益重要,他的基础是对水轮机调节系统的各环节提出准确的数学模型,不断探讨有关环节对过渡过程品质的影响。
孔昭年基于线性化系统计算分析了带调压井的水轮机调节系统稳定性[3],提出用双稳定边界表征它的稳定特性,即带调压井的水轮机调节系统稳定边界位于调压井时间常数分别为零和无穷大时水轮机调节系统稳定边界间的区域,从而大大简化了边界计算量。计算分析技术的进步可以考虑更多被忽略的非线性特性,更多地关注调节系统的过渡过程特性。本文在对带调压井的水轮机调节系统开展的计算分析中,采用流量、力矩的特征矩阵法描述水轮机特性、详细考虑了水轮机调速器非线性特性(如主配压阀速度特性、接力器开关时间整定引起的严重的非线性特性等),用实际算例说明调压井底孔阻尼对水轮机调节系统动态特性的影响和重要性。
2 过渡过程计算数学模型
2.1 引水系统数学模型
由图1所示引水系统,有带底孔调压井水轮机引水系统动力学方程及连续方程式组:
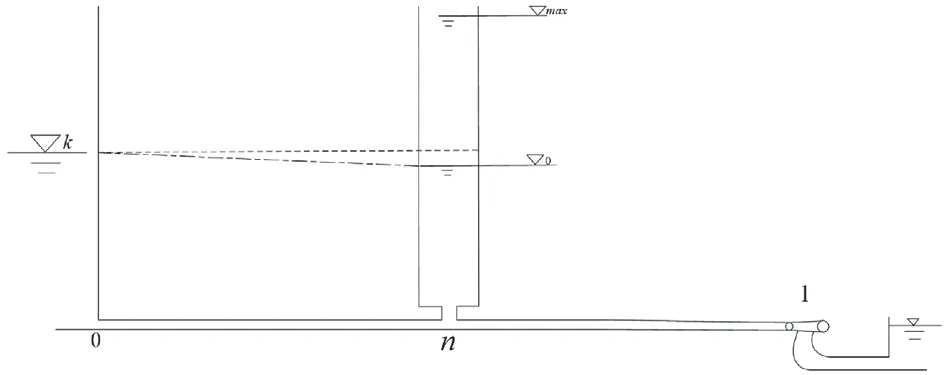
图1 引水系统示意
由水库进口到调压井底水流惯性时间常数Tw0n;调压井底至1号机的水流惯性时间常数Twni;调压井时间常数Te;α0n:0n段水头相对损失系数;αn1:n1段相对水头相对损失系数;
αn:内井底孔水头相对损失系数;采用相对微增的表达方式并定义有:微分算子;
流量相对偏差q;水压相对偏差h、调压井水位相对偏差z等,并配有相应位置角标。可以有载于图2的带调压井的水轮机引水系统计算原理图。
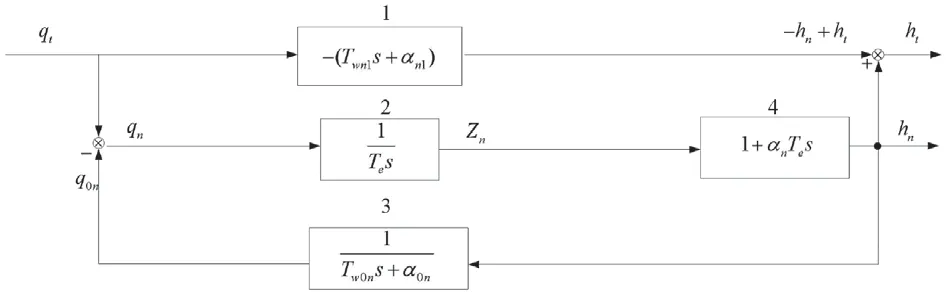
图2 引水系统计算原理图
2.2 水轮机数学模型
由水轮机单位流量、水轮机单位力矩、水轮机单位转速计算公式:
单位流量Q11=fq(a,n11)
单位力矩M11=fm(a,n11)
上述式中,Q:导叶开度;D1:水轮机转轮直径;H:水轮机水头;n:机组转速。有水轮机流量、力矩计算公式:
采用相对参数值计算方法用角标“o”表征稳态值;“r”表征额定值;“△”表征偏差值则有:
在线性化假设条件下,导叶相对开度α=Y/Ymax=α/αmax,由以上相应公式可有水轮机相对单位转速、流量、力矩计算公式:
在编制有关行业标准时,提出用水轮机流量和力矩的特性矩阵,计算水轮机流量和力矩值,有水轮机动态流量、动态力矩的计算表达式[4,5]:
该方法的优点是计算动态值时仅有加法和乘法,而没有除法,并确保求解非线性微分方程时快速收敛。我们已对纳入水轮机型谱的所有水轮机编制了专用的[(αq)ij]、[(αm)ij]数据文件,便于水轮机调节系统过渡过程计算采用。计算以HLA696模型转轮为例,根据其水轮机综合特性曲线可有图3、图4所示的水轮机流量特性、力矩特性曲线;载于表1的水轮机流量特性、力矩特性参数表及水轮机流量、力矩特性矩阵参数表。
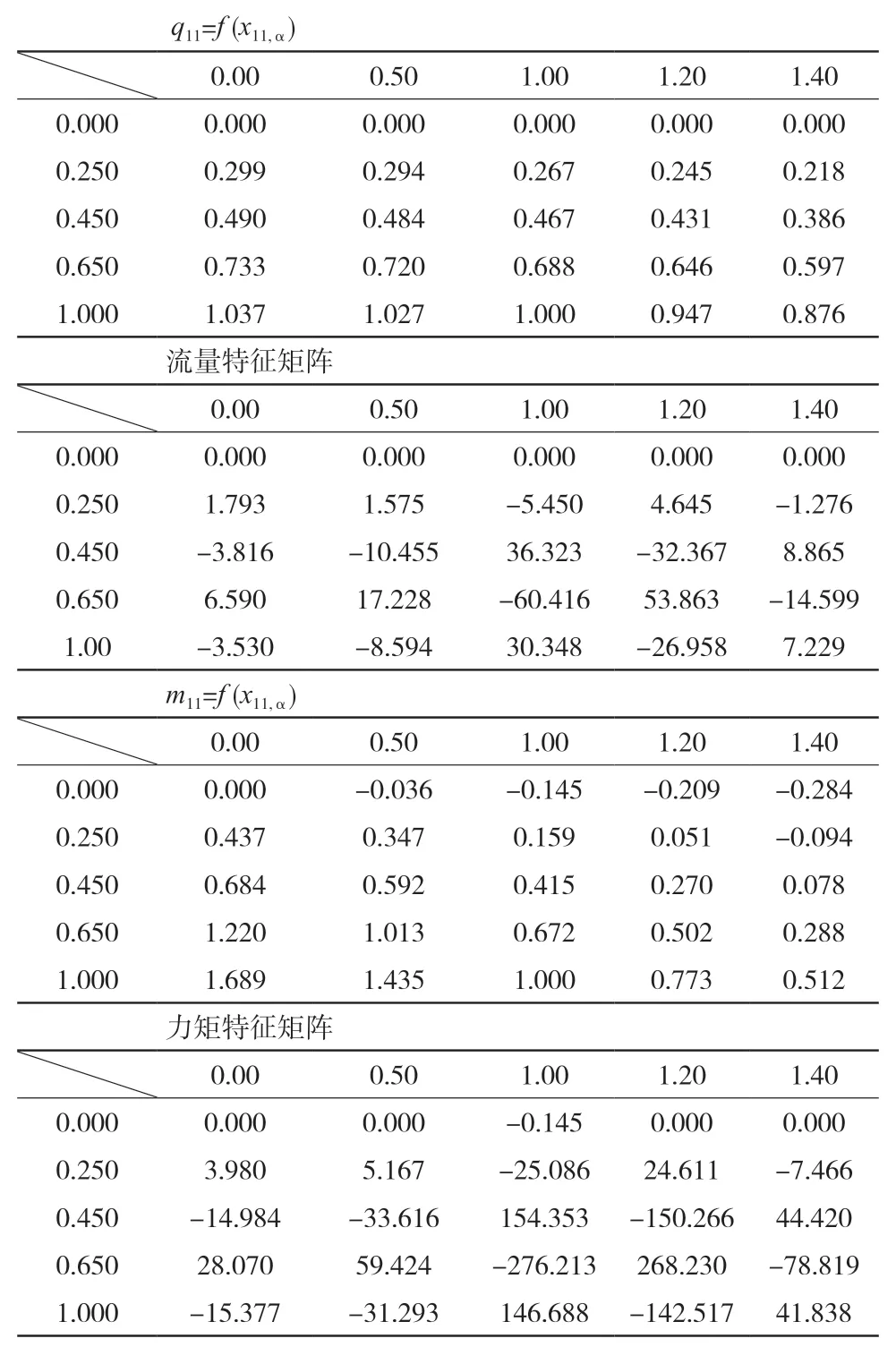
表1 水轮机流量特性、流量特征矩阵及力矩特性、力矩特征矩阵数据表
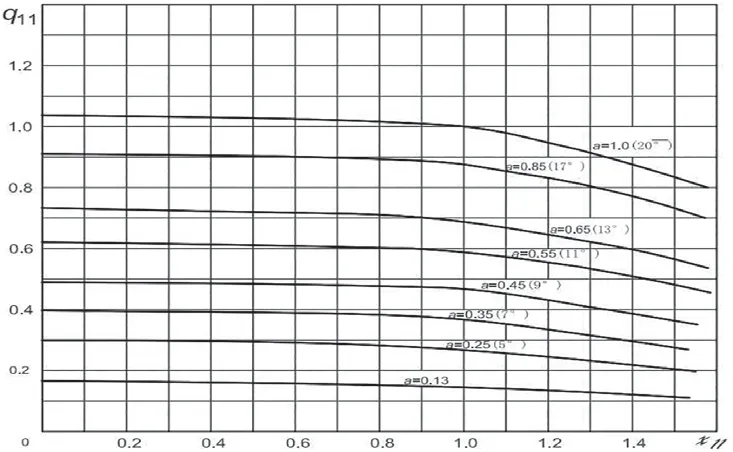
图3 水轮机流量特性曲线
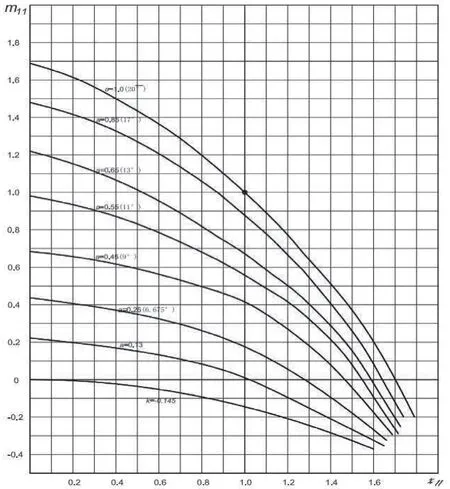
图4 水轮机力矩特性曲线
2.3 发电机方程式
式中:
Ta—机组惯性时间常数,Ta=GD2n02/365Pr;
Δm(t)—扰动力矩,增负荷为正。
2.4 水轮机调速器计算原理图
带调压阀水轮机调速器原理图见图5,其中Y(t):水轮机导叶接力器位移;Yv(t):调压阀接力器位移;调速器主配压阀特性见图6。我们积累的计算经验表明,在水轮机调节系统过渡过程计算中通常水轮机电液调速器测频环节有良好的线性特性,计算时不能忽略水轮机调速器配压阀的严重非线性,特别是调速器开关机时间整定引起的非线性特性。
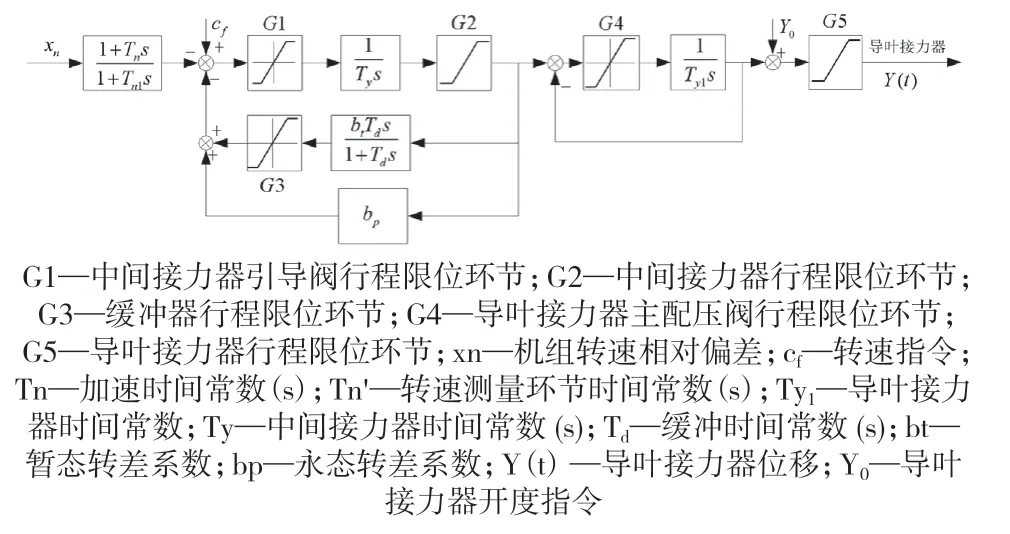
图5 水轮机调速器原理图
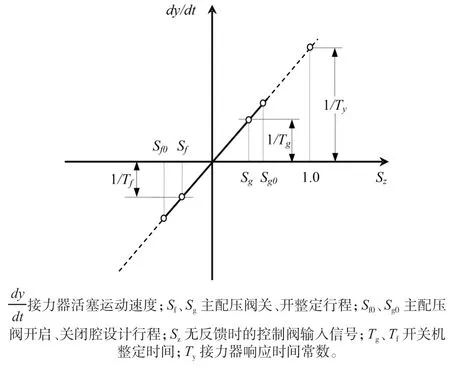
图6 调速器主配压阀的速度特性
3 带调压井的水轮机调节系统过渡过程计算
给定有关计算参数,将引水系统、水轮机、发电机、调速器动态方程式组联立,即可求解水轮机调节系统瞬态过程。有关参数汇总于表2。调压井井底阻尼系数分别取不同值,重点分析他的影响。水轮机甩100%负荷时过渡过程计算结果分别示于图7~图12。有计算结果可将有关指标性参数汇总于表3。

表2 控制系统主要技术参数表

表3 底孔阻尼对主要瞬变参数的影响
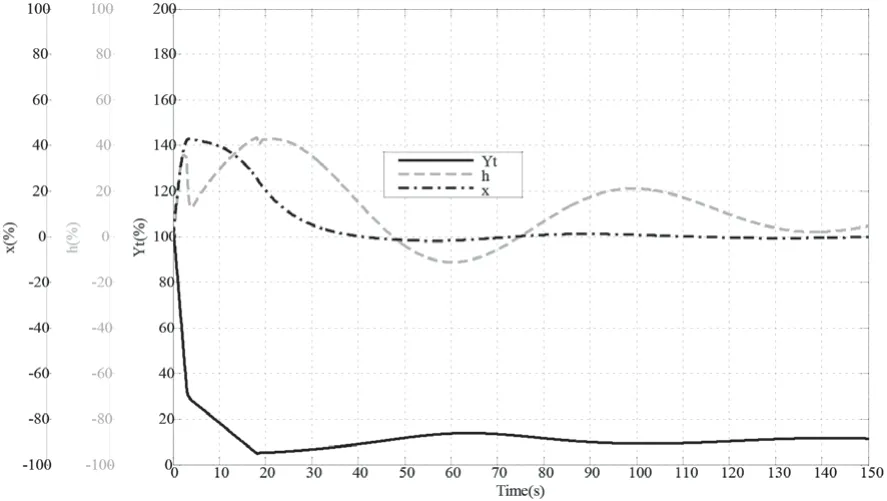
图7 甩100%负荷水轮机调节系统过渡过程αn=0.12;h:43.5%;x:43%
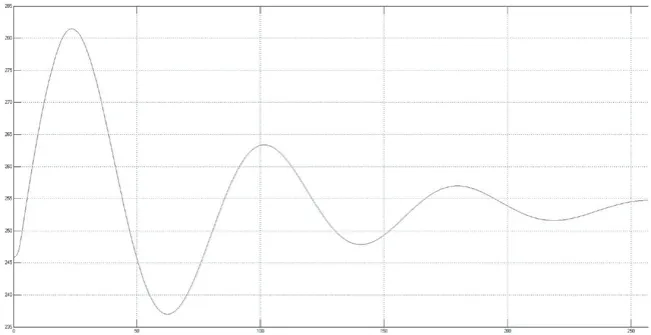
图8 甩100%负荷调压井水位波动αn=0.12调压井水位最大涌升35.64
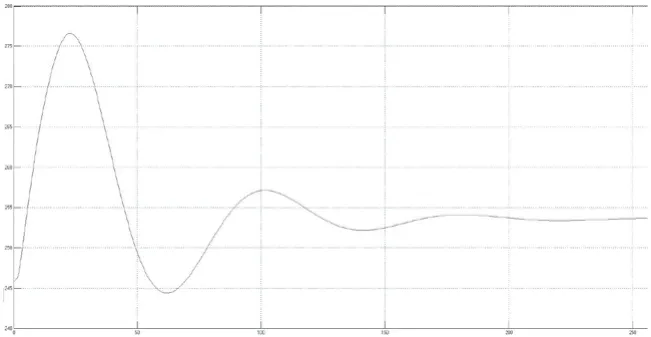
图10 甩100%负荷调压井水位波动αn=0.24调压井水位最大涌升30.74 m
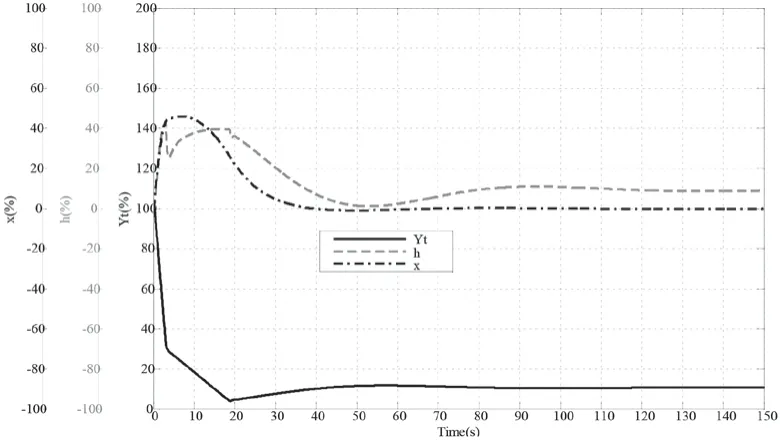
图11 甩100%负荷水轮机调节系统过渡过程αn=0.36;h:42.8 %;x: 46%
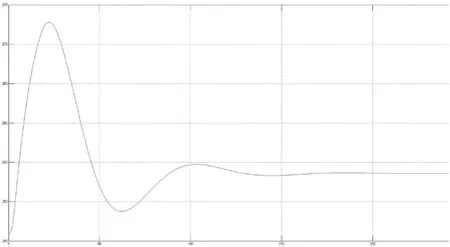
图12 甩100%负荷调压井水位波动αn=0.36 调压井水位最大涌升26.94 m
4 结论与讨论
通过计算证明在甩100%负荷条件下,系统稳定。通常关心调节保证条件并考核机组的相对转速偏差x的有关动态指标。当αn由0.12增大到0.36时,相对速率上升x由0.43增大到0.46;最敏感的是调压井内水位涌升由35.64 m减少到26.9 m。αn=0.12时水位波动在250 s尚在波动,当增大到0.36时水位到150 s时已趋于稳定水位。为进一步说明这一现象,由图2有调压井底压力传递函数,其分母表达式为:
条件时,调压井水位可以出现非周期性涌升过程,这是本文得出的重要结论。
调压井水位涌升现象随着αn由0.12增大到0.36,底孔阻尼增大,蜗壳波动现象逐渐减弱。当αn较小时,水轮机蜗壳水压力叠加有低频的压力脉动现象,致使水轮机蜗壳压力有局部突变及抖动现象。它与调压井涌升脉动同步,这种低频振荡很难用调速器参数加以矫正,这是带调压井的水轮机调节系统动态特性的重要特征,易引起共振现象,应引起注意。
由图2,定义h1=hn+ht,在图13~图15上载有由0.12增大到0.36时甩100%负荷3处压力的过渡过程计算,指标性参数计算结果汇总于表4。随着αn的增大,h1max、hnmax、(htmax)2均减小,而(htmax)1有所增大,水轮机蜗壳水压力因叠加有调压井水位低频的压力涌动现象(hn),致使水轮机蜗壳压力过程线有局部突变及抖动现象。这是带调压井的水轮机调节系统过渡过程的重要特点。

表4 底孔阻尼对压力上升的影响
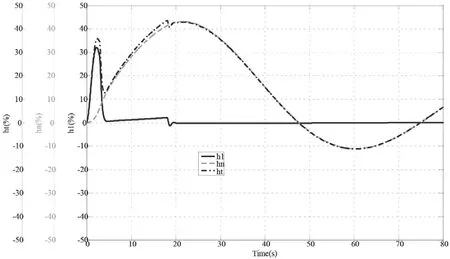
图13 αn=0.12甩100%负荷压力过程曲线h1max:0.322;hnmax:0.431;htmax:0.358和0.435
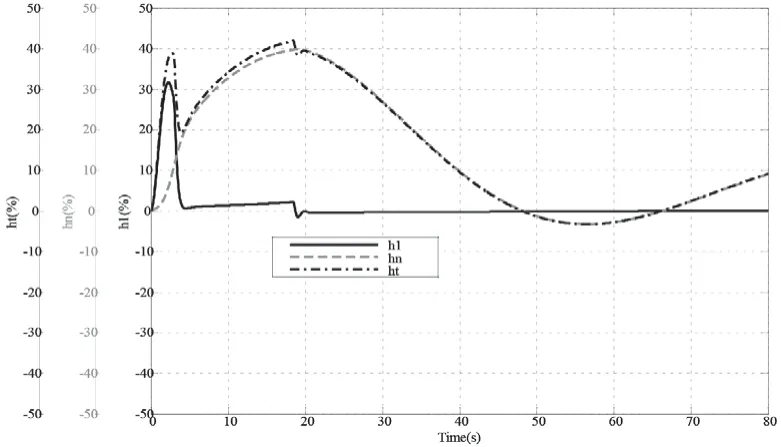
图14 αn=0.24甩100%负荷压力过程曲线h1max:0.317; hnmax:0.398; htmax:0.388 和0.42
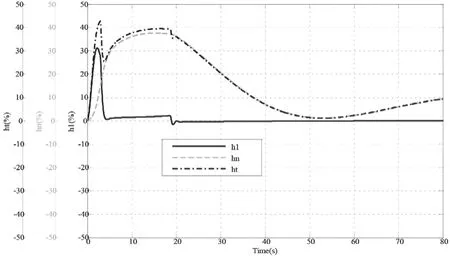
图15 αn=0.36甩100%负荷压力过程曲线h1max:0.312;hnmax:0.375;htmax:0.428和0.395
