三步接骨法治疗Sanders Ⅱ型跟骨骨折的有限元研究

李笑予， 张磊， 付磊， 李东波， 汪国友*

西南医科大学附属中医医院骨伤科，四川 泸州 646000

跟骨骨折是跗骨骨折中最常见的骨折类型，约占全身骨折的2%[1]，不论是选择保守治疗还是手术[2，3]，精准复位为其核心[4]。中医正骨手法在骨伤疾病诊治中有不可或缺的作用，具有操作简便、收费低廉、对骨折周围软组织及血运破坏小等优点[5]。结合临床经验，对于闭合型Sanders Ⅱ型跟骨关节内骨折，三步接骨法配合石膏固定或小夹板外固定是简便有效的治疗方案，其复位顺序大致为：拔伸牵引、提按顶复、端挤捏骨。三步接骨法临床疗效佳，但既往由于缺乏可视化的观察研究，难以对其有效性及安全性进行客观评价。有限元分析是一种使用数学过程的结构分析方法，可通过非侵入性的生物力学对手法进行研究，弥补整复效果评价主观性较强的不足，并为临床医生提供手法指导。目前，该方法多应用于推拿治疗的分析，而对正骨的研究较少。本研究基于前期的临床观察，采用有限元分析对三步接骨法治疗SandersⅡ型跟骨骨折进行探究，模拟不同手法作用的复位情况，客观验证该手法的有效性及科学性，促进其应用和推广。

1 材料与方法

1.1 研究对象

选取1 名健康成年男性志愿者，排除足部疾病与畸形。志愿者对实验步骤知情同意，伦理批准文号BY2022018。

1.2 研究方法

1.2.1 初始图像采集 图像采集由本院经验较丰富的CT 技师完成，采用SIEMENS Definition Edge 64 排螺旋CT（西门子公司，德国）获取数据，扫描间距0.75 mm，共376 张CT 图像，图像存储格式为DICOM，刻录于光盘中。

1.2.2 正常足踝模型与Sanders Ⅱ型骨折模型建立使用三维重建软件Mimics 21.0（Materialise 公司，比利时）对足踝CT 图像进行骨性结构分离，初步建立足部模型，储为STL 文件。将文件导入Geomagic Warp 2021（Geomagic 公司，美国）进行网格修复、模型光滑、皮质骨及松质骨划分。再使用Solidworks 2018（达索SIMULIA 公司，美国）对骨块进行组合装配及足部软骨绘制，完成正常足部实体模型的构建。依据跟骨骨折Sanders Ⅱ分型特点[6]，以30°半冠状面为基准面，在后距关节面最宽处从外向内标识A、B、C 三等分点，通过绘制穿过A、B、C 点的曲线，对跟骨骨块及部分软骨进行整体切割，并做适当位移，构建Sanders II A、Sanders II B、Sanders II C 型骨折模型（图1）。同时，人体韧带具有维持关节稳定性的作用，为更好地模拟足踝实际情况，在ANSYS 软件中（Ansys公司，美国），确定韧带解剖位置，使用“spring 单元”模拟韧带（表2），韧带刚度参考文献[7,8]，最终完成骨折模型构建（图2）。

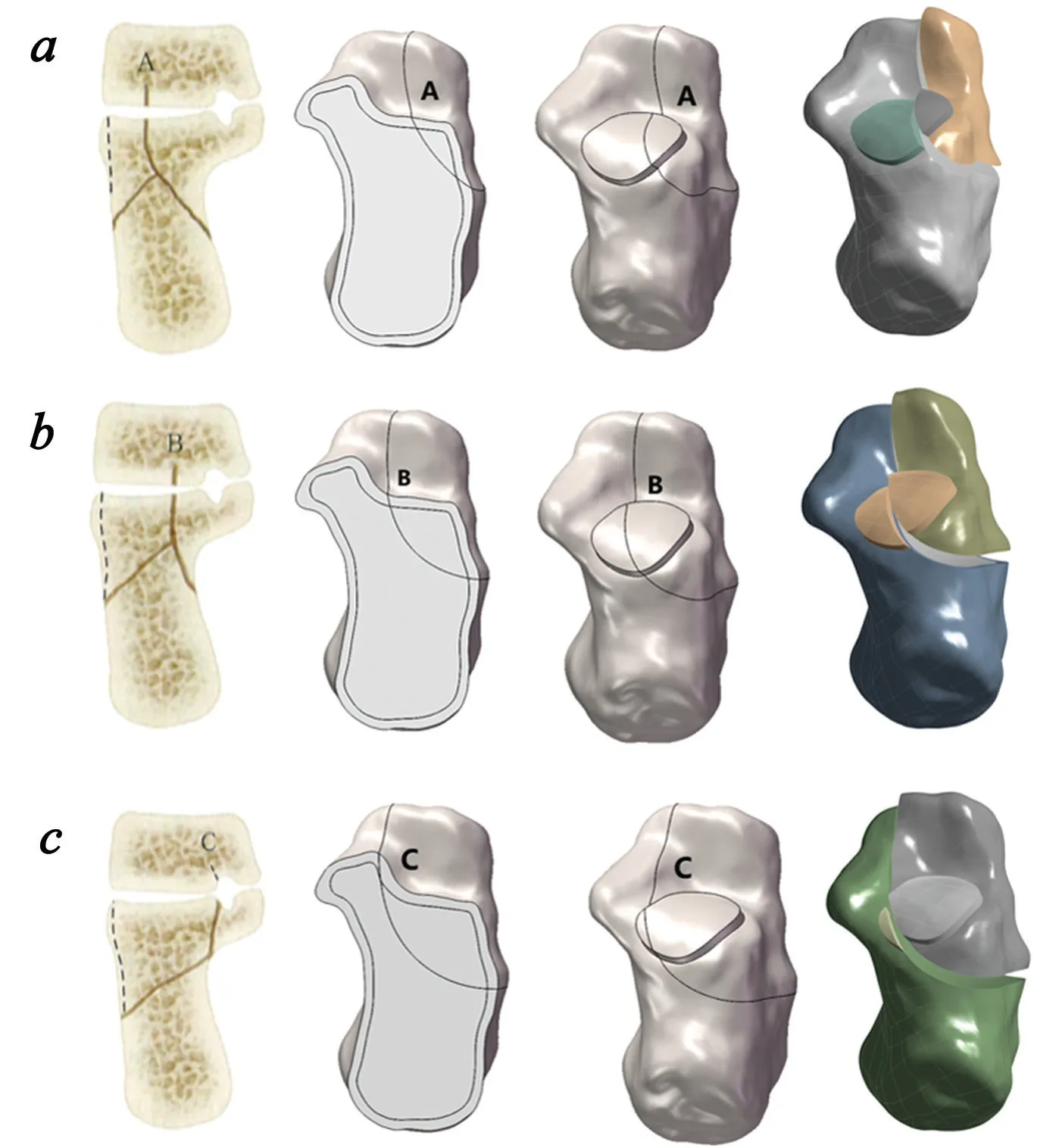
图1 Sanders II 型跟骨骨折模型示意图a：Sanders II A 型 b：Sanders II B 型 c：Sanders II C 型Fig.1 Schematic diagram of Sanders type II calcaneal fracture model. a: Sanders type II A model; b: Sanders type II B model; c: Sanders type II C model.

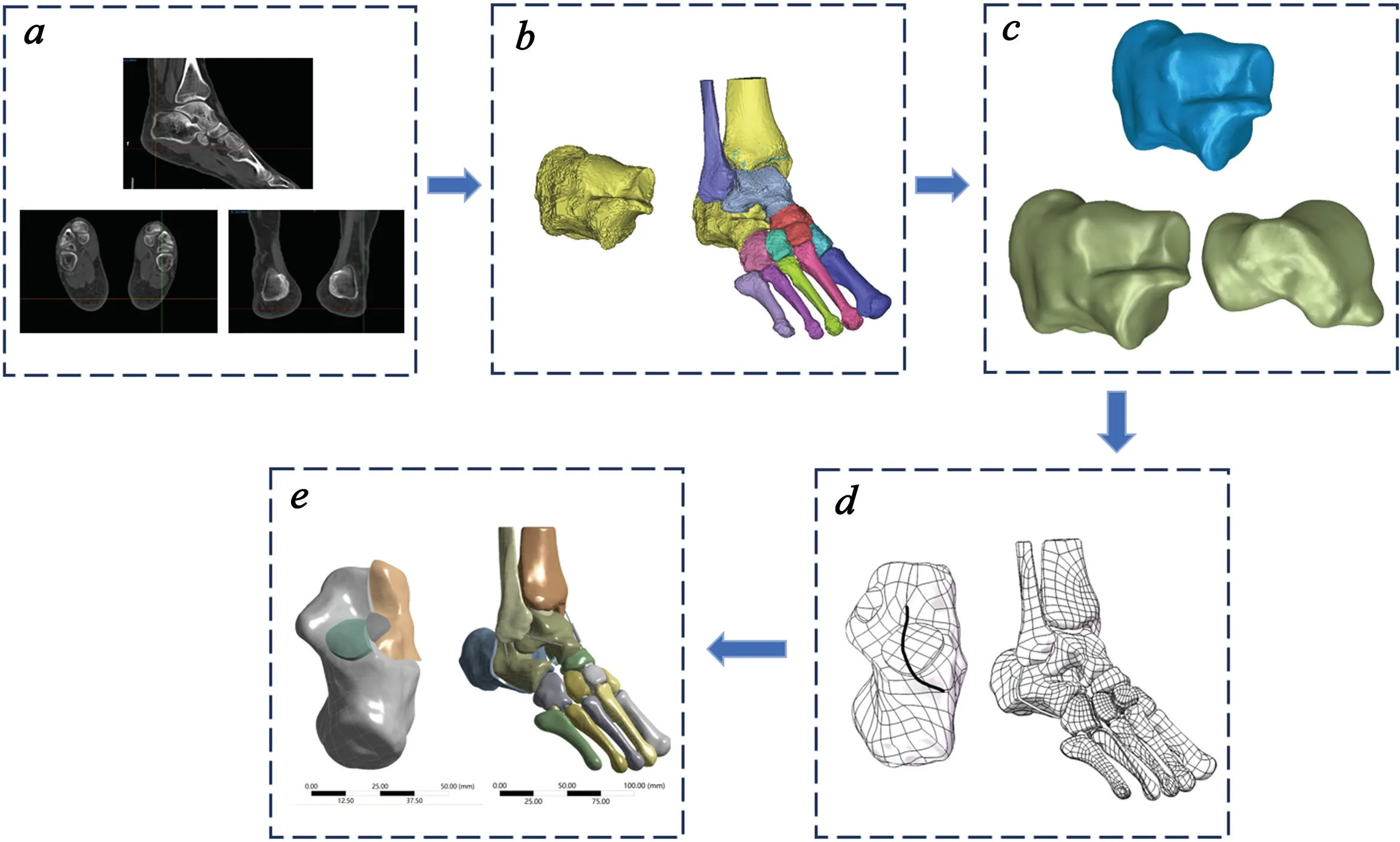
图2 建模流程图a：足部CT 图像采集 b：CT 数据提取（Mimics21.0）c：足部实体模型优化与光滑（Geomagic Studio 2021）d：模型装配（Solidworks 2018）e：有限元整体模型建立（Ansys Workbench19.2）Fig.2 Modeling flow chart. a: Acquisition of foot CT images; b: Extraction of CT data (Mimics21.0); c: Optimization and smoothing of foot solid model (Geomagic Studio 2021); d: Assembly of model (Solidworks 2018); e: Establishment of finite element integral model (Ansys Workbench19.2).

1.2.3 材料属性 本模型所涉及材料的力学特性均为均质和各向同性，材料的赋值依据目前认可的研究数据及相关文献，设定各材料特性参数如表1～2。定义皮质骨与松质骨的接触为“Bonded”，皮质骨和软骨的接触为“No Separation”。

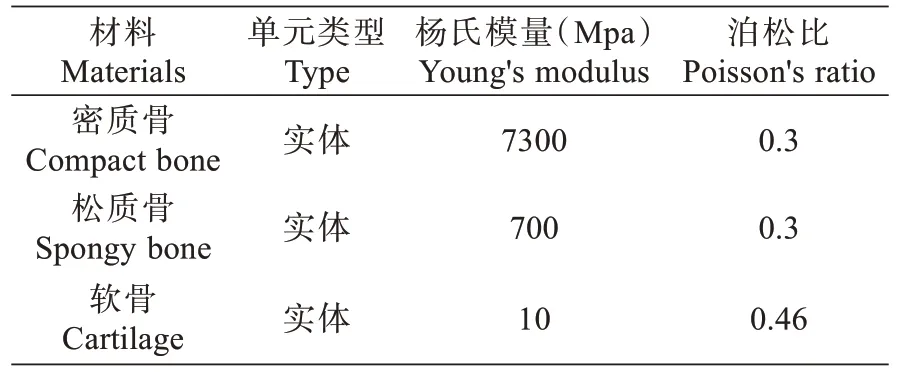
表1 单元类型及材料属性[9]Tab.1 Element types and material properties[9]

表2 足踝部韧带刚度（N/mm）[7,8]Tab.2 Stiffness value of ankle ligaments (N/mm）[7,8]

1.2.4 约束与载荷 首先对正常足踝有限元模型进行有效性验证。参考Anderson 等[10]的方法，根据实际情况，约束跟骨X、Y、Z 轴方向和舟骨X、Z 方向的自由度，于胫腓骨上截面施加600 N 垂直载荷，模拟踝关节中立位工况。再对Sanders II A/B/C 型骨折模型进行手法复位的加载，约束胫腓骨上端，进行分布位移载荷（图3）：第1 步在跟骨断端加载1 个Y 方向2 mm 位移载荷，模拟拔伸牵引手法；第2 步在跟骨断端加载1 个Z 方向1 mm、1 个负Y 方向2 mm 位移载荷，模拟提按顶复手法；第3 步在跟骨断端加载1 个负X方向2 mm 位移载荷，模拟端挤捏骨手法。

图3 Sanders ⅡB 型跟骨骨折模拟手法复位a：模拟拔伸牵引b：模拟提按顶复c：模拟端挤捏骨▲代表边界条件Fig.3 Simulated manipulative reduction of Sanders type II B calcaneal fracture. a: Simulation of traction and extension techniques; b: Simulation of lifting and pressing techniques; c: Simulation of pinching and joining techniques; ▲represented boundary conditions.

2 结果

2.1 踝关节模型有效性验证

建立了正常足部模型与Sanders II A/B/C 型跟骨骨折有限元模型，解剖结构清楚，模型平滑，四面体单元数目多，单元大小适中，正常模型节点总数534570，单元总数322444。正常模型沿力线垂直施加600 N 轴向力后，计算得出胫骨下穹隆关节接触面积为479.18 mm2，最大接触应力为3.10 Mpa，与Anderson 等[10]实验结果对比基本一致，证明该模型有效。

2.2 Sanders II 型跟骨骨折有效复位

模拟三步接骨法进行加载后骨折实现有效复位（图4,5），复位流程逼真，并成功进行了力的求解（表3）。将Sanders II 型3 种骨折同类复位手法的力学数据汇总，求解每步手法的力学趋势（图6）。发现：拔伸牵引法主要施力于Y 轴，致力于恢复跟骨长度，有效纠正重叠位移；提按顶复法重点施力于Z 轴，致力于恢复跟骨高度，有效纠正前后侧位移；端挤捏骨法施力于Y、Z 轴，致力于恢复跟骨宽度及Gissane's 角等，有效纠正内外侧位移。

图4 三步接骨法分步加载总变形量结果图a：完成第一步拔伸牵引b：完成第二步提按顶复c：完成第三步端挤捏骨Fig.4 Step loading total deformation result diagram of three-step reset method. a: Completed the first step of traction and extension; b: Completed the second step of lifting and pressing techniques; c: Completed the third step of pinching and joining techniques.

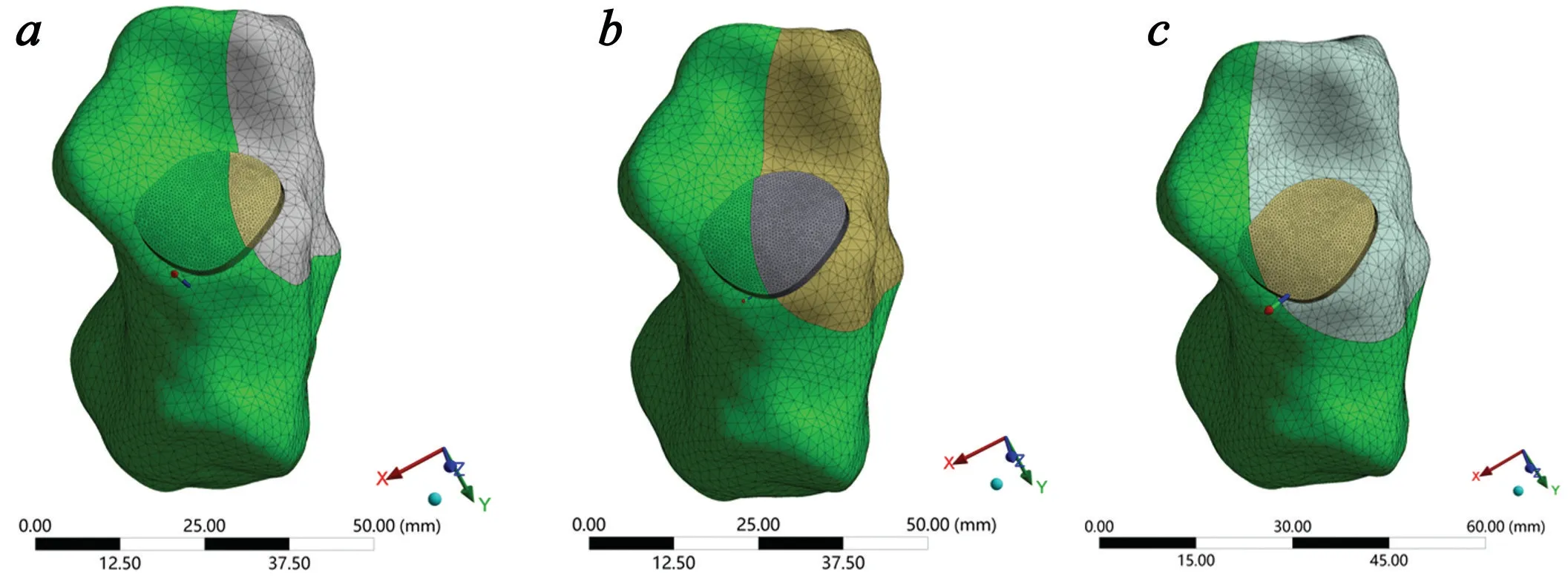
图5 Sanders ⅡA/B/C 复位结果a：Sanders ⅡA 模型复位图b：Sanders ⅡB 型模型复位图c：Sanders ⅡC 型模型复位图Fig.5 Reduction results of sanders II A/B/C. a: Reset diagram of sanders II A model; b: Reset diagram of sanders II B model; c: Reset diagram of sanders II C model.

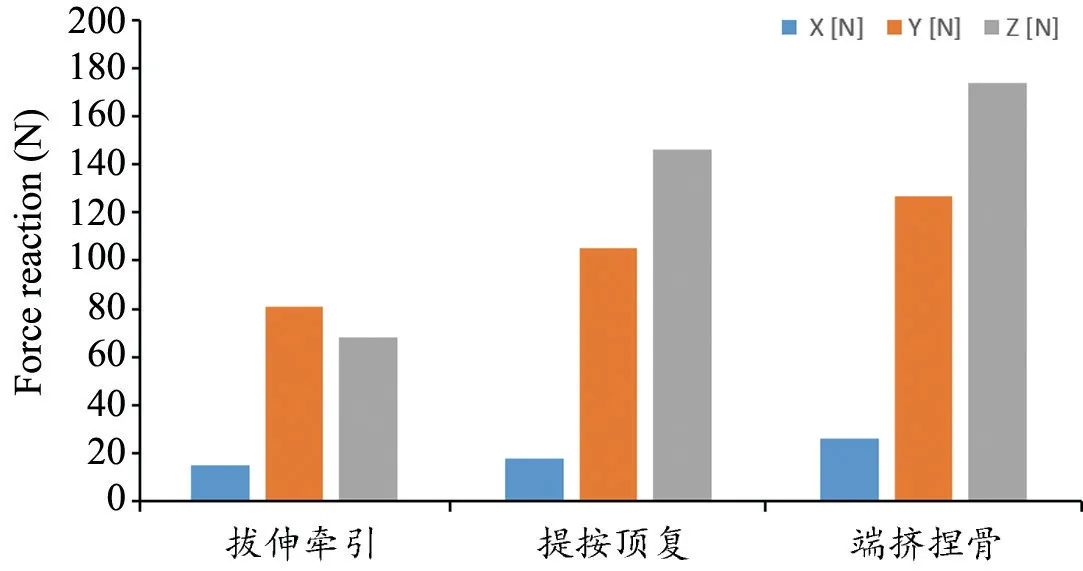
图6 不同手法X/Y/Z 轴的力学变化趋势Fig. 6 Mechanical trends of force in X/Y/Z axis for different manual techniques.

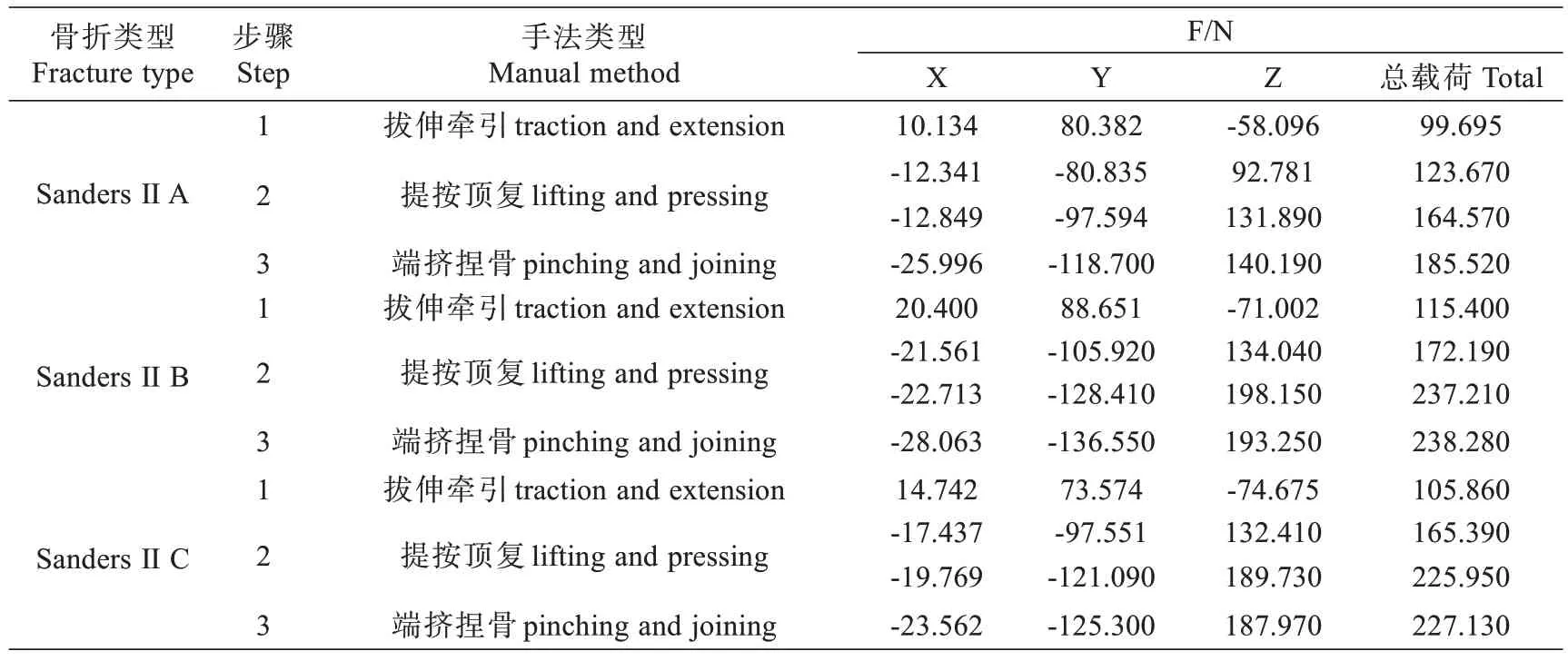
表3 位移载荷与力的求解（N）Tab.3 Solution of displacement load and force

通过测量Sanders II A/B/C 有限元模型复位前后跟骨长、高、宽、Gissane's 角、Bohler's 角等数值（表4），复位后跟骨畸形得到明显纠正，跟骨解剖参数平均恢复：长2.57 cm、高4.43 cm、宽2.89 cm、Gissane's 角5.94°及Bohler's 角5.94°。复位过程中，骨折端平均应力峰值12.1 Mpa，未造成骨质、韧带与软骨等损伤，证实手法的有效性及安全性。表3 中部分力学求解数据偏小，原因可能是模型缺少皮肤、部分肌肉等维持足底形态的结构，缺乏与手法对抗的力，但本实验目的是探究手法复位时骨块整体运动方向及力学变化趋势，故认为该模型有意义，后期尚需完善。

3 讨论

跟骨骨折是一种常见的严重后足损伤[11]，多由直接暴力所致，由于跟骨具有多关节面且形态极不规则的解剖特点，正确的骨折分型及精准的建模在明确跟骨损伤程度、选择治疗方案以及评估预后中发挥重要作用。前期相关研究已完成单块跟骨骨折建模，而缺乏对足部整体骨、软骨及韧带的建立，本次研究针对跟骨特征及手法复位适应症，对Sanders II 型骨折进行直观、立体和精准的模型建立，完善足踝骨块、添加多个关节软骨及关键韧带，并严格依据Sanders II 型解剖特性进行骨折线划分，为研究跟骨骨折损伤及治疗模型提供参考。既往研究将骨材料默认为骨密质，忽略了骨松质的影响，而Wang 等[12]研究肯定了骨小梁在承载负荷、分散应力中的重要作用。基于此，本研究对骨块的骨密质、骨松质也进行有效区分，尽可能实现有限元模型仿真。

中医手法复位是骨伤科四大疗法之一，具有疗效佳、创伤少、费用低等优势。然而，往昔缺乏客观的评判标准和研究方法，正骨手法推广受限、科学性受到质疑。随着计算机技术的高速发展和有限元方法的广泛应用，其可视化、精准化及规范化的特点为手法的研究提供了新的途径，弥补了操作无法客观化、标准化的不足，刘广伟等[13]应用有限元探讨旋前-外旋型三踝骨折逆移位手法复位的可行性，温海宝等[14]通过建立足踝模型探讨手法治疗踝扭伤的力学作用机理。目前关于跟骨骨折的研究集中于内固定受力分析[15]，关于正骨复位的研究偏少，且缺乏标准化复位步骤及流程。因此，本研究通过有限元模拟手法整复过程中跟骨的挤压、扭转等情况，精确进行了手法加载，克服了传统生物力学实验不能准确赋值的短板，着力实现手法的复现，为传统手法的研究提供丰富手段和技术支撑。

三步接骨法是依据中医正骨临床经验，结合跟骨骨折特性而总结提出，此手法以“筋骨并重”理论为指导，坚持骨与筋共同调治、整体与局部复位相结合，在Sanders II 型骨折的闭合复位中具有独特的优势。结合实验结果，本研究手法加载步骤符合复位流程，实验过程中骨折断端应力峰值较小，未见骨质或主要韧带损伤，说明该复位法的安全性。同时，复位前后跟骨的宽、长、高、Gissane's 角及Bohler's 角均得以明显改善，验证了正骨手法的有效性。根据三步接骨法求解的力学趋势及相关临床经验，进一步总结完善三步接骨法复位方案：（1）整体拔伸牵引法：手摸心会，拔伸牵引。结合跟骨骨折的损伤类型及影像学特征，细触骨折部位，确认骨折移位情况后，按照“欲合先离，离而复合”的原则，采用拔伸牵引手法沿跟骨纵轴作相反牵引，用于恢复跟骨长度、韧带长度及张力，有效改善跟骨重叠位移；（2）局部提按顶复法：上提下按，丝丝入扣。针对骨折前后移位，遵循“陷者复起，突者复平”原则，使骨折两端对合，恢复跟骨高度；（3）局部端挤捏骨法：内推外按，相互挤扣。针对左右位移，手掌从足跟两侧扣挤，将向外突出的骨折端向内挤迫，在纠正左右移位的同时尽可能地恢复跟距关节面、跟骨宽度、Gissane's 角及Bohler's 角。整骨后再进行周围软组织调理：理筋续断，畅达肌腱。于踝关节、跗骨周围按照肌腱、肌的方向从上到下顺骨捋筋，使扭转的肌肉、肌腱随骨块复位而舒畅，实现对“骨与筋”的整体把握。此复位法不是简单凭经验随意施加整复，而是循筋摸骨、按序正骨，在临床实践中有效减少对骨与软组织造成二次损伤，尽可能避免创伤性关节炎，更好恢复距下关节面的平整。

本研究存在某些局限性：首先，因加载条件限制，模型未纳入跟骨骨折断端的旋转及成角畸形，即重叠、旋转、成角及侧方移位同时存在的情况，但临床上旋转移位往往可以通过牵引纠正，模型周围肌及皮肤等软组织也将在后续研究中进一步完善；其次，仅探究三步接骨法手法步骤及流程的可行性，未能进行手法量化研究，在后续研究中需运用力学测量与运动捕捉技术，精确手法角度、方向和力等参数，进一步实现手法规范化与普及化。

综上，本文利用有限元法初步构建Sanders II 型跟骨骨折模型并进行手法复位加载，在三步接骨法的分步载荷下，跟骨畸形显著改善，结合手法的力学特征，临床医生可进一步完善复位方案。同时，本文也为客观验证正骨手法疗效、规范复位步骤提供可靠的研究手段。结合临床观察，三步接骨法创伤小、疗效快、复位良好，是治疗Sanders II 型跟骨骨折一种有效和安全的方法。本研究为跟骨关节内骨折的闭合复位提供了新思路，其手法量化及机制研究值得进一步探索。