基于Kokkos模板元编程的性能可移植求解器开发

郑亮，黎坤运，周兴彬，李永辉，于要杰，向玉开，胡健，柴华，郭黎,2

1.国家超级计算成都中心，四川 成都 610213 2.成都数据集团，四川 成都 610041

引 言

根据美国能源部高性能计算系统的发展路线设计，新的超算系统将采用包括同构CPU 和异构CPU+GPU 两种模式，而GPU 又包括了NVIDIA、AMD 等不同硬件架构，导致了技术路线各异，随之而来编程模型和应用开发呈现出散乱无序、重复研发等问题。为了解决该问题，美国能源部（DOE：Department of Energy）组织的E 级计算计划（ECP：Exascale Ccomputing Project）资助了若干项目来应对，它们解决问题的手段统称为：性能可移植（Performance Portability）[1-3]，包括Kokkos、RARJ、SYCL等项目[4-8]。

性能可移植是指软件在不同处理器上实现可移植编译、部署，并能保持和发挥出处理器性能的编程方法。早期的性能可移植尝试主要是使用OpenCL 来实现[9]，希望利用OpenCL 在不同异构设备上的兼容性，从底层实现性能可移植，但从后期实践来看效果并不理想。ECP资助的性能可移植项目主要使用C++模板元编程（Template Meta-Programming）实现，利用模板的抽象性特征，编写统一的调用接口，同时针对不同的硬件设备编写实现，在编译期确定代码类型，甚至可以在编译期实现计算从而提高执行性能，Kokkos 和RAJA 都是采用该方法[4-6]。国内对性能可移植的直接讨论并不多，更多地是希望使用性能工程方法针对某一架构实现最优化的解决方案[10]，但仍然也有从领域特定语言角度去考虑性能可移植的初步尝试[11]，此外许多工作采取了解耦技术，例如算子解耦技术[12]、代码自动生成技术[13]都隐含了性能可移植的编程思想。

模板元来自C++模板编程[14]，是泛型编程的一种实践，最早不是一种编程模型，是在实际使用中逐渐被发现和提炼的一种图灵完备的编程方法。由于模板元可以在开发期不确定函数类型，这特别适合各种不同异构计算设备的代码转换，因此被用于性能可移植软件开发。

数值计算是高性能计算最为重要的应用场景之一，本文根据数值计算特征总结了4层性能可移植模型（图1），从上到下分别是：（1）性能可移植应用：有限元、有限差分、有限体积、分子动力学等计算软件；（2）性能可移植算法：主要包括Trilinos 和PETSc 等通过对Kokkos 支持实现性能可移植；（3）性能可移植框架：包括Kokkos、RAJA和SYCL等美国E级计算框架；（4）性能可移植编程：主要是具体用C++模板元对各种编程语言、编程方法的封装，包括分布式计算MPI、同构多核OpenMP、异构众核CUDA/OpenCL/HIP等。

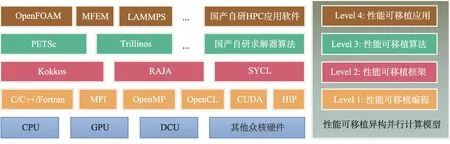
图1 性能可移植异构并行计算层次划分Fig.1 Layered diagram of performance portable computing on heterogeneous devices

目前，国际上性能可移植的工作主要集中在Level 1和Level 2，同时Level 4有一部分的应用，例如Lammps 通过对Kokkos 框架的支持实现跨异构设备计算[15-16]。Level 3 方面的工作是缺失的，虽然Kokkos是Trilinos项目的一部分[17]，且PETSc 也编写了对Kokkos 的接口[18]，但实际应用并不多。因为高性能计算软件在计算机上的具体实现高度依赖于线性代数求解器算法，所以本文初步尝试还是针对Level 3-线性代数求解器接口编程方面的工作做一些挑战。综合考虑RAJA 和Kokkos 后，选择了维护和开发更为成熟的Kokkos 作为基础框架，使用C++模板元对Kokkos 部分功能进行再封装，初步实现了线性代数求解器开发接口的开发，并给出了Krylov 子空间算法的部分求解器实现案例和性能分析。

1 Kokkos介绍

Kokkos是美国E级计算计划重点支撑的并行框架，能支撑HPC 底层库在不同异构架构上的移植。Kokkos 底层采用C++编写，是可适配所有主要HPC 平台的“性能可移植”编程模型。为满足性能可移植的需求，Kokkos 为并行执行的代码及数据管理提供抽象，旨在针对具有N级内存层次结构和多种执行资源类型的复杂节点体系结构。Kokkos为了隔离科学计算软件开发对硬件的依存，其基本思想是导入一个中间层隔开硬件与应用软件。硬件依存关系在这个中间层中处理，而应用软件则无需过多考虑硬件实现问题。在此基础上，应用层的开发人员也许会失去对硬件层的细节控制，但是可以降低编程门槛，节省软件开发时间，得到通用可移值的软件[19-20]。

Kokkos生态系统包括Core代码、数学内核、分析和调试工具以及文档教程等。Kokkos Core是Kokkos 系统的核心部分，是一种面向硬件的并行编程模型，为代码的并行执行和数据管理提供了抽象。目前可以使用CUDA、HIP、Open-CL、OpenMP和Pthread等作为后端编程模型，适用于N 级内存层次结构和多种类型执行资源的复杂节点架构。Kokkos只是负责计算节点内的并行计算，计算节点间的分布式并行计算需要由其他软件来实现。并行执行编程可由并行模式Pattern、执行策略Policy以及并行计算的执行空间Body实现。模式Pattern有并行循环for、规约、扫描等并行模式，策略Policy有循环范围、调度策略、指定硬件等通过指定模板参数选择，空间Body是并行执行的内容。除了数据结构和并行执行外，Kokkos Core 编程模型还提供了随机数生成和排序等基本算法，Vector、Array、Map、Csr、MemPool等容器。Kokkos通过良好的接口设计，把内存对齐、下标映射、异构设备内存和主内存之间的通信同步等封装起来。用户可以通过统一的接口，按需要选择硬件设备而无须处理其具体执行的细节，只需要适当的调整模板参量就可对应各种不同硬件上的并行计算。

2 性能可移植求解器编程

性能可移植编程项目ChipSum 是成都超算中心高性能计算部性能优化研发工程师发起开发的一款开源异构并行计算框架，寓意为覆盖不同芯片的开发。ChipSum 旨在用于构建跨不同硬件架构的性能可移植求解器编程，目前已支持x86/ARM/CUDA/ROCm等不同主流架构。

ChipSum的架构如图2所示，最底层用模板元编程封装实现了面向不同异构编程框架的后端泛型模板接口，向下兼容Kokkos、RAJA、SYCL和CUDA、HIP等后端，在后端接口的基础上编写了部分对标BLAS的代数算子模板接口，在最顶层编写了线性代数求解器接口（ChipSum.Solver），并同时尝试针对深度学习算法实验了算子编写（ChipSum.AI）。

图2 性能可移植求解器编程框架ChipSum架构图Fig.2 Architecture of Chipsum,a performance portable solver programming framework

2.1 模板元编程后端泛型接口

ChipSum目前实现了基于Kokkos框架编写统一的数值线性代数编程算子调用接口。在编程中，主要使用type_traits 特性萃取技术实现编译器计算、判断，实现操作符类型的自动选择。本文定义了最基本的操作符：

其中，sparse_mat_type和vector_type实际为double类型CSR格式稀疏矩阵及向量类：

2.2 代数算子模板接口

在代数算子接口方面，使用模板方法实现了4 种常见类，包括标量接口Scalar，向量接口Vector，稀疏矩阵接口SparseMatrix，稠密矩阵接口DenseMatrix。标量接口Scalar 主要是标量计算的Device端实现，导入头文件方式：

标量接口类的描述如下：

标量接口成员函数主要实现了从设备端取回数据GetData()，从设备端打印Print()等基本操作。向量接口Vector 主要是向量计算的Device端实现，导入头文件方式：

向量接口类的描述如下：

向量接口成员函数除了基本的GetData()、GetSize()、Print()以外，主要实现了加法算子Add()、减法算子Sub()、加乘算子AXPBY()、点乘算子DOT()、乘法算子Mult()、求负数算子Neg()、向量1-范数Norm1()、向量2-范数Norm2()、向量的Inf范数NormInf()等。

稀疏矩阵接口SparseMatrix 主要是稀疏矩阵计算的Device端实现，导入头文件方式：

稀疏矩阵接口类的描述如下：

稀疏矩阵支持CSR、COO等常用格式，稀疏矩阵接口成员函数除了基本的GetData()、GetNNZ()、GetColNum()、GetRowNum()、Print()以外，主要实现了稀疏矩阵乘向量算子SPMV()和稀疏矩阵乘稠密矩阵算子SPGEMM()等。

稠密矩阵接口DenseMatrix 主要是稠密矩阵计算的Device端实现，导入头文件方式：

稠密矩阵接口类的描述如下：

稠密矩阵接口成员函数除了基本的GetData()、GetColNum()、GetRowNum()、Print()以外，主要实现了稠密矩阵相乘算子GEMM()和稠密矩阵乘向量GEMV()等。

2.3 求解器模板接口

Krylov 子空间（KSP）算法是最常见也最简单实现的现代迭代法求解算法，通过残差与误差的关系：

其中，r(i+1)是Ad(i)的线性组合，而不同的d(i)是相互正交的线性无关向量。对于第i个迭代步的结果，是在d(i)为基组成空间Di中找寻到的，Ad(i)是其中一个子空间，那么Di可以用以下的子空间张成，表示为：

其中，找寻的d就是残差r，即寻找的子空间是：

这个子空间即称为Krylov子空间。

对于求解一个Ax=b问题，如果需要m个迭代步得到收敛，不妨把叫做这些迭代步残差r组成的空间叫做m维仿射子空间，记作Km，把上面Krylov子空间重写为：

将此空间叫做搜索空间。

为了找到解，需要构建前述d组成的空间，把这个空间叫做约束空间，记作Lm，满足：

对不同约束空间的选择则构成了不同的Krylov子空间求解器算法，又称KSP求解器：

（1）Lm=Km，正交投影求解器，该方法可以极小化误差的能量范数，共轭梯度法（CG）求解器即为该类；

（2）Lm=AKm，斜交投影求解器，该方法可以极小化残差的2 范数，广义最小残差法（GMRES）求解器即为该类；

（3）Lm=Km(AT,r0)，即约束空间为A转置的Krylov子空间，属于约束空间和搜索空间的相互正交，又叫双正交，BiCG和BiCGStab即为该类。

以上是最常用的3类KSP求解器，如果构造更加复杂的约束空间，例如对以上3类空间的混合使用，则可以构建出更多的KSP求解器。KSP求解器算法实现相对简单。在ChipSum 提供的代数接口基础上，只需要简单的进行算子组合即可实现。在ChipSum 源代码的示例目录里给出了共轭梯度家族的3种求解器实现方法，分别是CG-Conjugate Gradient、BiCG-Biconjugate Gradient、BiCGStab-Biconjugate Gradient Stab 算法，同时也实现了简单的GMRES算法。

为了验证结果的正确性，本文以CG为例测试了ChipSum 与SciPy 的对比，通过两组矩阵：1）STD矩阵：Matlab帮助给出的demo矩阵，样式如图3 所示，是有限差分离散的标准对称矩阵，包含49,600 个非零元；2）PDE 矩阵：来自MFEM软件包给出的DG 法离散稀疏矩阵，样式如图4所示，形态较为复杂，但仍然是对称正定矩阵，包含24,320个非零元。图5是两组实验的对比，可以看出无论是求解STD 矩阵，还是求解PDE矩阵，ChipSum 与SciPy 残差收敛几乎完全一样。证明ChipSum 求解器接口开发在准确性上得到了验证。

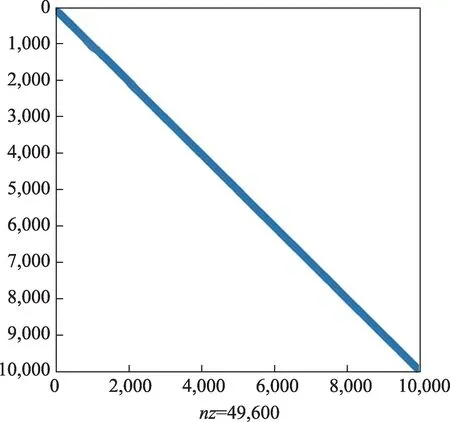
图3 用于验证的测试STD矩阵样式Fig.3 STD Matrix’Pattern

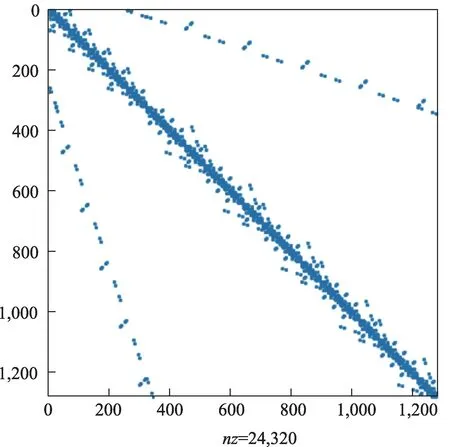
图4 用于验证的测试PDE矩阵样式Fig.4 PDE Matrix’Pattern

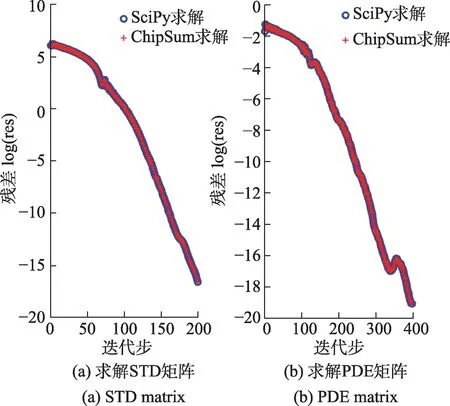
图5 ChipSum和SciPy求解残差对比Fig.5 Comparison of solved residual between ChipSum and SciPy

3 性能测试

3.1 基础算子性能

求解器编程的性能主要取决于稀疏矩阵乘向量SPMV（Sparse matrix-vector multiplication）算子。由于稀疏矩阵有任意稀疏模式和大小，SpMV的异构并行化存在包括内存合并、线程分歧和负载不平衡等问题，有较大的优化空间。基于ChipSum开发的CSR结构矩阵SPMV 算子优化加速方法主要包括：（1）采用动态分配行的方法，代码根据输入矩阵每行平均非零元素的数量启动不同版本的内核来优化线程的负载平衡；（2）内存访问优化，通过共享内存存储每个线程块对应的行偏移量，减少全局内存的访问；（3）寄存器向量化规约优化，利用线程束洗牌指令，数据在寄存器中完成向量行乘积的规约操作[21]。

GFLOPS (Giga Floating- point Operations Per Second)即每秒10 亿次的浮点运算数，常作为硬件性能参数。CSR格式的稀疏矩阵乘中每个元素有两个浮点运算，因此GFLOPS=2×N/(t×109)，其中，N为稀疏矩阵非零元素个数，t为SPMV 的计算时间[22]。计算得到了ChipSum 在不同处理器上执行指定SPMV的性能如图6所示。

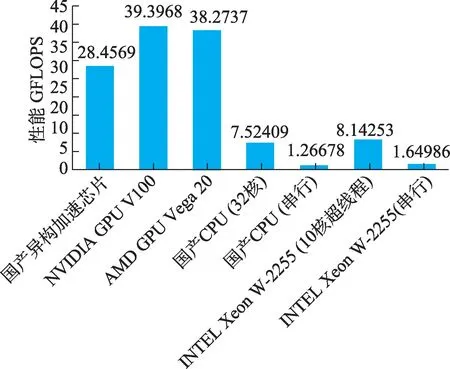
图6 ChipSum SPMV算子在不同处理器上性能对比Fig.6 Performance comparison of ChipSum SPMV operators on different devices

实际上，目前优化过的ChipSum 针对国产异构加速器实现最新的SPMV 已经能够超过原生Kokkos 性能，而相比ROCm 生态自带的hipsparse 库性能提升更加明显。本文测试了Matrix Market 给出的若干矩阵，得到如图7 所示SPMV性能，证明ChipSum的SMPV性能已优于Kokkos原生性能。

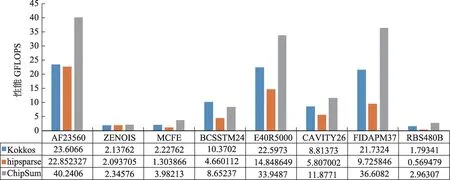
图7 Kokkos、hipsparse和ChipSum实现SPMV算子在国产异构加速卡上的性能对比Fig.7 SPMV performance on a heterogeneous device implemented by Kokkos,hipsparse and ChipSum

3.2 求解器性能

本文对ChipSum 实现的求解器在不同平台上的实现也做了对比。目前基于ChipSum 实现了CG、BiCG、BiCGStab 和GMRES 4 种常用求解器，对CG、BiCG 和BiCGStab 测试一组6,400万阶大小的矩阵，GMRES由于暂未实现重启操作，受限于片上内存本文仅测试了一组900万阶大小的矩阵，主要测试其计算100个迭代步的求解耗时，得到结果如图8 所示。可以看到，基于ChipSum 实现的GMRES 算法相比10 核CPU 有接近40x 的加速。国产异构加速芯片的性能能达到V100 的70%左右，与两种芯片的理论峰值相匹配。

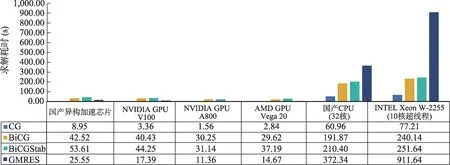
图8 ChipSum实现CG、BiCG、BiCGStab、GMRES性能在不同处理器上的对比Fig.8 Performance comparison of ChipSum implemented CG,BiCG,BICGStab and GMRES on different devices

4 结论与展望

基于Kokkos设计了跨平台性能可移植线性代数求解器编程框架ChipSum，能成功适配OpenMP、HIP 及CUDA 环境，能实现CPU 与GPU 设备的混合编程，能潜在用于多样化异构计算设备的数值计算程序开发。在性能表现上，国产异构计算设备性能在部分问题下相比于10 核CPU 具有数十倍以上的性能提升，实现了性能可移植的初衷。ChipSum 所有源代码均已开源（托管地址为：https://gitee.com/chip-sum/ChipSum）。

ChipSum 将继续作为一款面向性能可移植的实验性科学计算中间件，朝着高可用、高可扩展的方向发展。在功能接口上，ChipSum将持续集成更多的高性能计算算子，包括但不限于Sp-GEMM、Sort、GraphColoring、QR、LU、ILU等；在计算效率上，ChipSum 将集成诸如Level Stage DOT、Light SpMV、ESC SpGEMM、BH Sp-GEMM 等多种优势算子的优化方案；在架构设计上，ChipSum也将持续对现有的泛型设计架构进行优化，面向用户保证框架化的调用模式，面向后续开发者保证流程化的协同开发规范；在硬件适配性上，更多、更丰富的硬件芯片将依托ChipSum 的Backend Core 无缝对接上层的代数功能接口，助力构建ChipSum 与更多国产芯片的循环生态。

利益冲突声明

所有作者声明不存在利益冲突关系。

附录A

CPU 硬件平台配置：国产X86架构CPU，32核，频率2.0 GHZ；英特尔X86 架构CPU，至强W-2255 10 核（超线程20 线程），频率3.7 GHZ。异构硬件加速平台包括国产异构加速卡、AMD VEGA20 显卡、NVIDIA V100 GPU，配置参数如下表：

表1 异构设备性能指标对比Table 1 Comparison of heterogeneous devices’performance