基于静力触探试验及土工参数的黏性土空间变异性研究

马明 叶冬明 陆军 任守勤 陈浙徽

（1.中铁一局集团建筑安装工程有限公司，陕西西安 710054；2.杭州地铁开发有限公司，浙江杭州 310019；3.浙江工业大学土木工程学院，浙江杭州 310014）

0 引言

自相关距离δ是岩土参数空间变异性的重要指标，是指土层中参数不相关点间的最小距离，即小于δ时土体参数基本上是相关的，反之，大于该距离时土体参数不相关。作为岩土勘察原位测试方法，静力触探试验（CPT）测得的土体参数能够连续地反映土层竖向变化情况，且具有效率高、经济性强等优点，被广泛应用于岩土勘察中，如土层分类、土的物理力学指标确定[1]、地基液化判别[2]、单桩竖向承载力计算以及岩土参数空间变异性的计算等[3]。

计算自相关距离的常见方法有平均跨距法、统计模拟法、递推空间法、地质统计法、曲线极限法、相关函数法等方法。近年来，一些研究者基于静力触探数据对不同地区的土体参数的自相关距离及变异性进行了计算并统计归纳[4-5]。郭林坪等[6]基于静力触探试验分析了自相关距离计算方法和影响因素，并对计算方法进行了改进。朱登峰等[7]通过计算得出空间相关函数法与递推平均法两者计算结果差异较大。李镜培等[8]依据大量实际工程测试得到的土性参数，通过多种方法进行计算，最终确定出地区性自相关距离代表值。

此外，一些学者还分析了不同地区自相关距离计算方法的适用性。李芃[9]通过静力触探数据及土工试验测得的物理参数、变形参数和水力参数统计分析了合肥地区非饱和黏土的自相关距离。朱红霞等[10]统计出天津港地区典型土层的相关函数及自相关距离，并将其用于港口边坡稳定性的可靠度分析。林 军等[11]采用多种自相关模型拟合了江苏地区黏土波动分量的自相关系数，得到沿深度方向呈现明显的分层趋势。马 欢等[12]根据北京地区实际工程勘察资料，通过分析抗剪强度指标的变异性和相关性，计算出抗剪强度指标的自相关距离。由于不同区域土性参数的空间变异性具有一定的差异，因此有必要研究不同地区环境情况下的最优自相关距离计算方法。依托浙江嘉兴某围垦区的246 组静力触探试验及18 个钻孔取土土室内试验参数，采用平均跨距法、递推空间法和曲线极限法计算研究区土体的垂直和水平自相关距离，研究该地区土体自相关距离的最优计算方法，并对比分析基于锥尖阻力、摩擦阻力和多个土性参数的自相关距离的特点。本项目的研究结果对总结该地区土体参数的波动范围、变异规律具有重要意义，可为岩土工程设计提供更可靠的参数取值依据。

1 自相关距离的计算方法

自相关距离是衡量土体参数在区域一定距离内两点之间关联程度的一个重要标准，当空间两点距离小于该距离时，则认为土体两点之间是相关的。自相关距离概念出现之后，国内外学者对此做了深入的研究和探讨，出现了多种求解自相关距离的方法。本研究采取平均跨距法、递推空间法、曲线极限法计算自相关距离，具体方法介绍如下。

1.1 平均跨距法（PKF）

平均跨距法是Vanmarcke[13]提出的确定自相关距离的简便方法，通过土体参数变化曲线与趋势线分量曲线交点间的平均距离来计算。

式中：为土体参数曲线和趋势线交点间的平均距离；δ为所求的自相关距离。

1.2 递推空间法（DKF）

递推空间法是通过方差折减函数Γ2(h)来求解自相关距离δ，h为取样间距的倍数，方差折减函数实质是随机场的空间平均方差与点方差之比。方差折减函数为

式中：Var(h)为h的方差函数；σ2为点方差；当h足够大时，δ为一常数，在 Γ(h)-h图上的表现为：当h取一系列值后，绘出Γ (h)-h曲线，确定曲线将趋于平稳时h的平均范围值h*，以该值计算自相关距离δ=h*Γ2(h*)。

谭晓慧等[14]提出了一种新的平稳点的确定方法，即：将 Γ(h)-h曲 线转换为hΓ2(h)-h曲线，随着h增加，曲线hΓ2(h)-h呈现先上升后下降的趋势采用中间取峰值点处的纵坐标值为自相关距离。本研究采用相同方法。

1.3 曲线极限法（QJF）

记y=h，选取合适的函数z=f(y)对曲线z=hΓ2(h)进行拟合优化。拟合函数需要满足以下条件，当y趋于无穷大时，z=f(y)函数的极限值存在且为小于等于1 的常数；当y＜δ 时，有Γ2(y)＜1。同时满足相应的拟合精度。

本研究采用冷伍明等[15]提出的拟合函数（见式（3））进行优化拟合，其中参数a和b通过最小二乘法获得，最终可推导出对应的自相关距离为δ=1/b。

2 自相关距离的计算与统计

2.1 工程现场情况

用于评估自相关距离的静力触探试验原始数据均来源于浙江省某围垦区，经现场勘察可知，该区地表向下的土层依次为：冲填土层、黏土层、淤泥质黏土层、粉质黏土层。土体含水率为20.3%～40.5%，孔隙比为0.705～1.377，重度为14.11～20.24 kN/m3。

在研究区范围内进行了246 组静力触探试验的测试，同时设置了18 个取土孔开展室内土工试验，具体位置如图1 所示。静力触探垂直取样间距均为0.1 m，钻孔深度为30～45 m。由于计算自相关距离时要求试验样本为等间距采样，故本研究采用246组静力触探试验数据计算垂直自相关距离，用图1虚线框内的9 个钻孔间距均为25 m 的静力触探试验数据计算水平自相关距离。图1 中空心点为取土孔，其采样深度为40～45 m。获得土样后，通过室内土工试验得到一系列土工参数，包括烘干法测含水率、环刀法测天然密度与天然孔隙比，计算湿密度、干密度，比重瓶法测土粒比重，毛细管饱和法测量计算饱和度，液塑限联合测定法测得液限、塑限、塑性指数、液性指数，根据压缩试验e-p曲线计算压缩系数和压缩模量。由于取土孔较离散，未能满足水平自相关距离的计算要求，故本研究只计算基于土工参数的竖直自相关距离，并和基于静力触探数据的自相关距离进行比较。

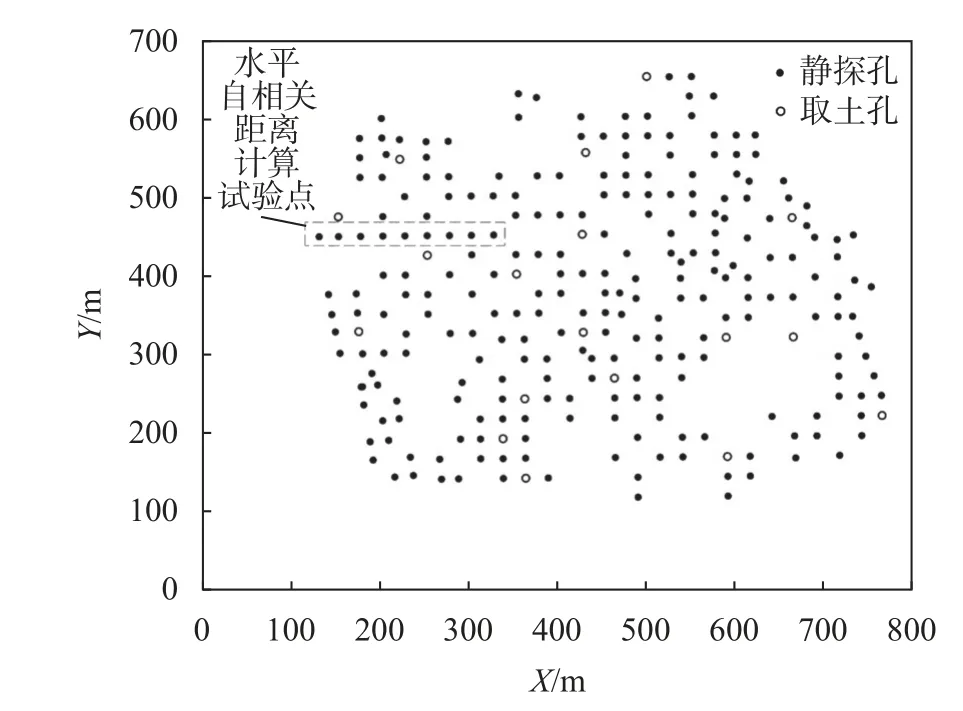
图1 场地钻孔位置示意图

2.2 数据的预处理

对原始数据进行前处理以获得平稳性较好的随机数据，是应用随机场理论分析土体空间变异性的前提。最常用的前处理方法是去趋势法，即对沿深度z变化的原始测试数据g(z)进行预处理，将其分为两部分（见式（4）），一部分是趋势函数t(z)，反映了数据沿着深度变化的趋势；另一部分是随机波动分量x(z)，其具有零均值、平稳性的特点。

以锥尖阻力qc为例，采用去趋势法进行前处理的结果如图2 所示。趋势项的拟合函数如图2（a）的虚线，具体表达式为t(z)=0.099z-0.3866，将趋势项从原始函数中去除后即得到波动项x(z)，如图2（b）所示。采用闫澍旺等[16]文中的方法进行了平稳性验证，得到去趋势的结果后可进一步计算相应的自相关距离。

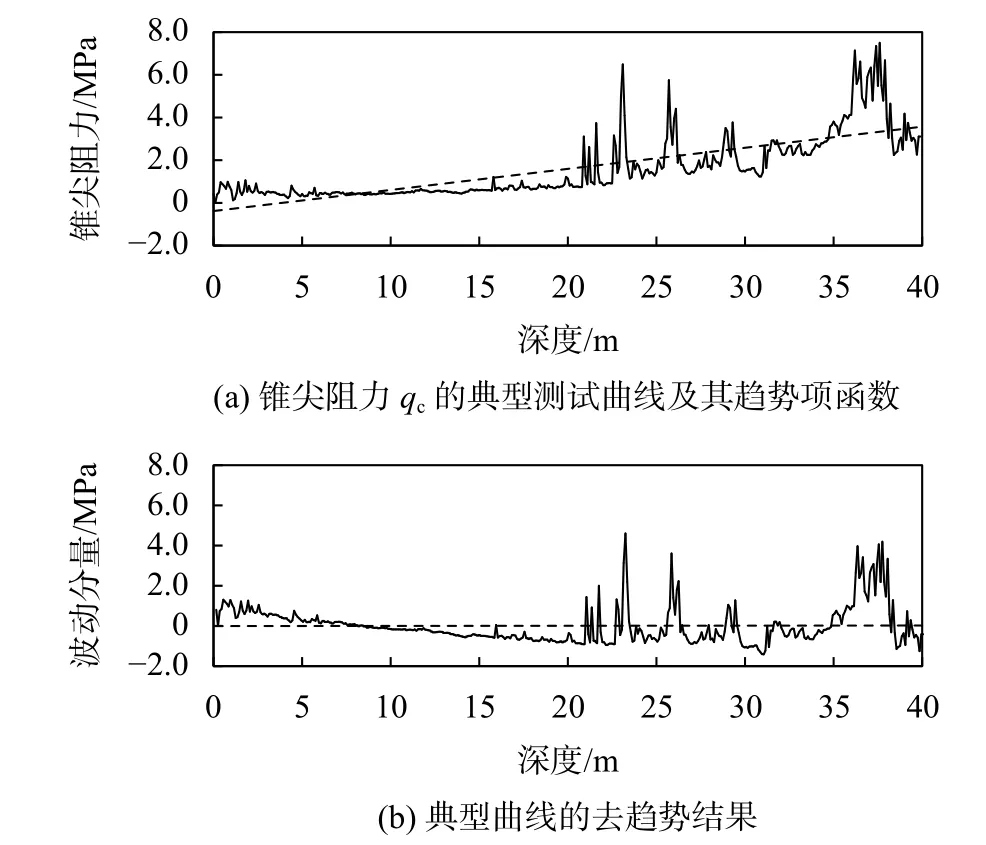
图2 静力触探试验数据的预处理（以锥尖阻力为例）

2.3 基于静力触探数据的垂直自相关距离计算

将静力触探试验测得的侧阻力fs、端阻力qc数据进行预处理后，应用前文提出的3 种方法计算土体的自相关距离。以静力触探的最小采样间距0.1 m作为垂直自相关距离δv的计算间距h，利用 246 组数据分别计算得到δv，再求其平均值作为研究区域的δv代表值。表1 汇总了静力触探相关参数数据以及3 种方法计算δv的结果。通过对照可知，fs的垂直自相关距离计算值略大于qc的垂直自相关距离计算值。

表1 基于静力触探参数数据计算的垂直自相关距离δv

图3 为3 种方法计算静力触探参数所得自相关距离的箱型图。图3 中部矩形上下两边分别为上下四分位点，矩形内部方形点为平均值，矩形中横线则为中位数，上方菱形实心点代表异常值。从图中可以看出3 种方法中平均跨距法计算结果异常值较多，离散性较大，因而造成计算结果明显小于其他两种方法，而另外2 种方法计算得到的计算结果较为稳定，异常值少。递推空间法、曲线极限法2 种方法中，递推空间法的变异系数较小，分别为0.38 和0.43，更适合该地区应用。

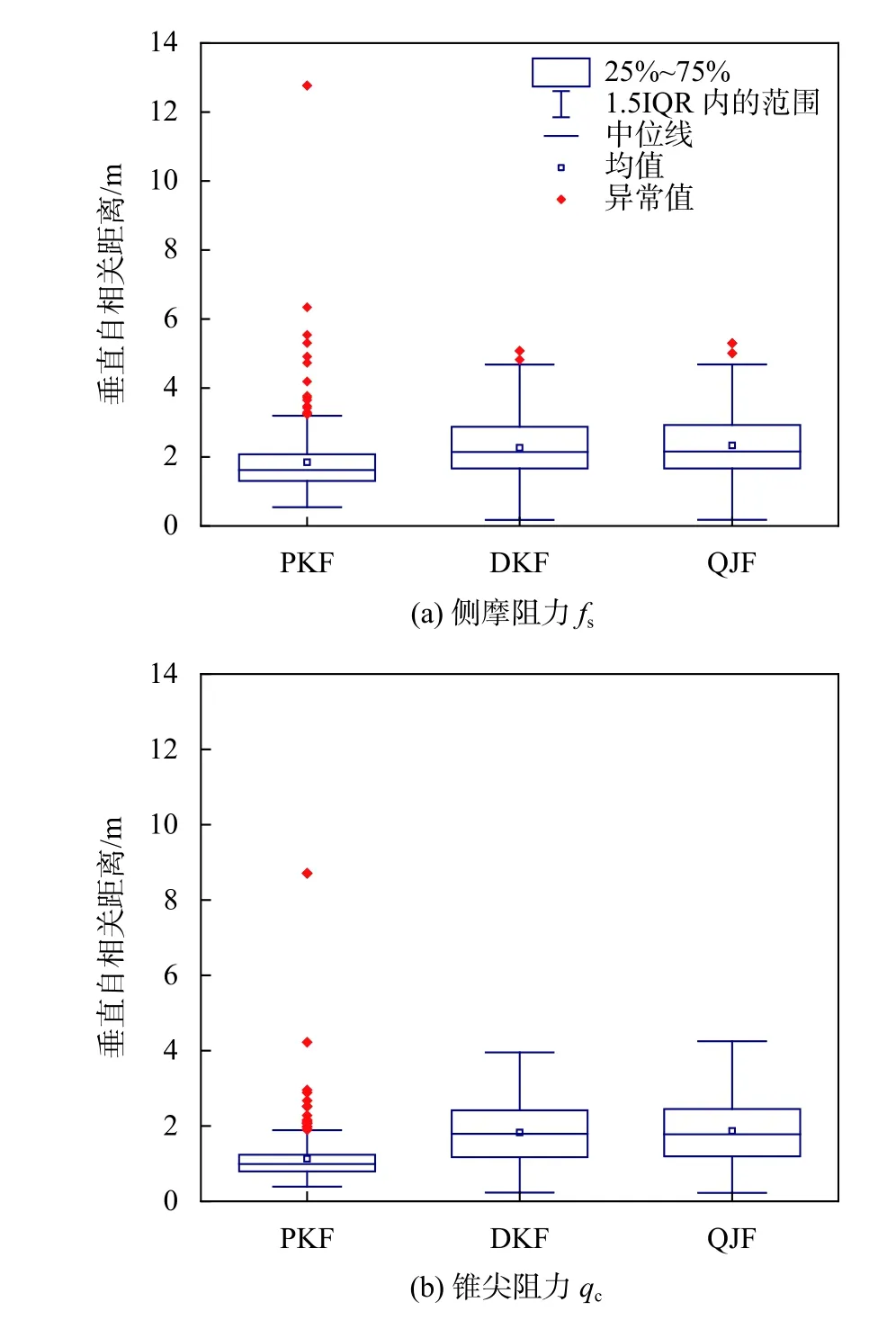
图3 3 种方法计算的静力触探参数的垂直自相关距离箱型图

2.4 基于静力触探数据的水平自相关距离计算

取图1 虚线框内的9 个静力触探孔计算水平自相关距离，其钻孔间距均为25 m，钻孔深度均为45 m，每隔0.5 m 选取静力触探数据，共分析90 组样本的水平自相关距离δh，结果如表2 所示。对比发现，平均跨距法的计算结果明显大于其他两种方法，且其范围较大，表明该方法在处理较离散的数据时有一定的局限性，造成较大的误差。此外，与垂直自相关距离计算情况不同，fs的水平自相关距离计算值均小qc的水平自相关距离计算值。

表2 基于静力触探参数数据计算的水平自相关距离 δh

基于3 种方法计算得出的δh的箱型图见图4。从图中可以看出，平均跨距法的异常值较多，不建议取用。对比递推空间法和曲线极限法在计算δv和δh的表现可知，递推空间法的变异系数最小，故推荐使用该方法计算该地区的自相关距离。与其他研究成果[5,17]对比发现，研究区垂直自相关距离范围与均值都略大，水平自相关距离则偏小。说明该地区的土层竖向相关性较好，水平向相关性较小。

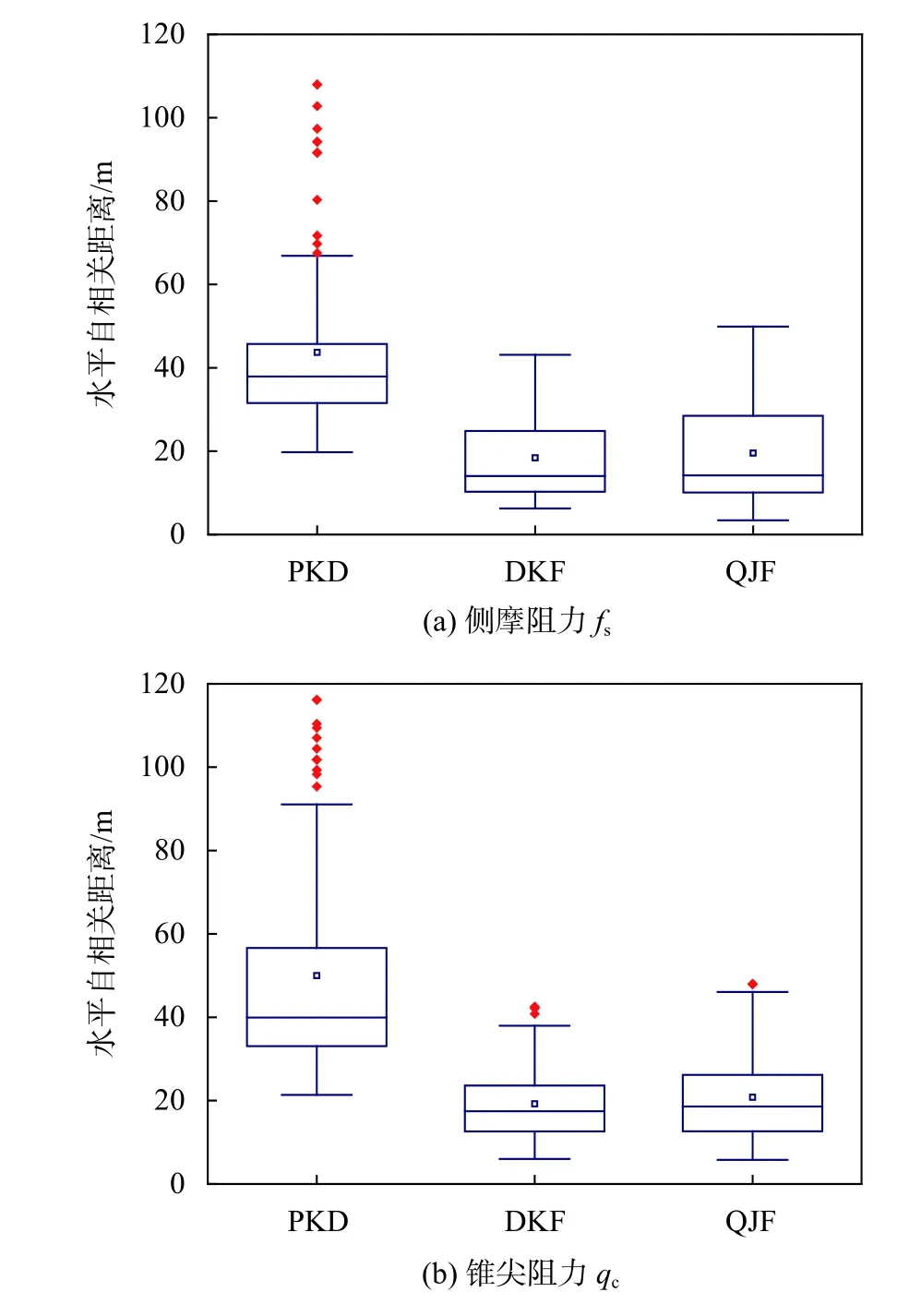
图4 3 种方法计算的静力触探参数的水平自相关距离箱型图

2.5 基于土工参数的垂直自相关距离计算

在18 个钻孔取土试验得到的系列参数数据中，选取含水率、湿密度、干密度、土粒比重、孔隙比、饱和度、液限、塑限、压缩系数、压缩模量共计12 个参数进行垂直自相关距离计算。

3 种方法计算土工参数的垂直自相关距离结果如表3 所示，在计算方法上看来，平均跨距法的计算结果都偏大，而递推空间法与曲线极限法的计算结果相差不大。数据点较少时，采用平均跨距法会造成参数函数与趋势项函数交点少，此时会过高估计其自相关距离。由于不同参数的性质不同，计算得到的δv也会有一定的差距，但本研究的目的是最优计算方法的选择，主要是找出同一参数下不同计算方法的优劣，所以参数不同造成的差距对方法选择影响较小。

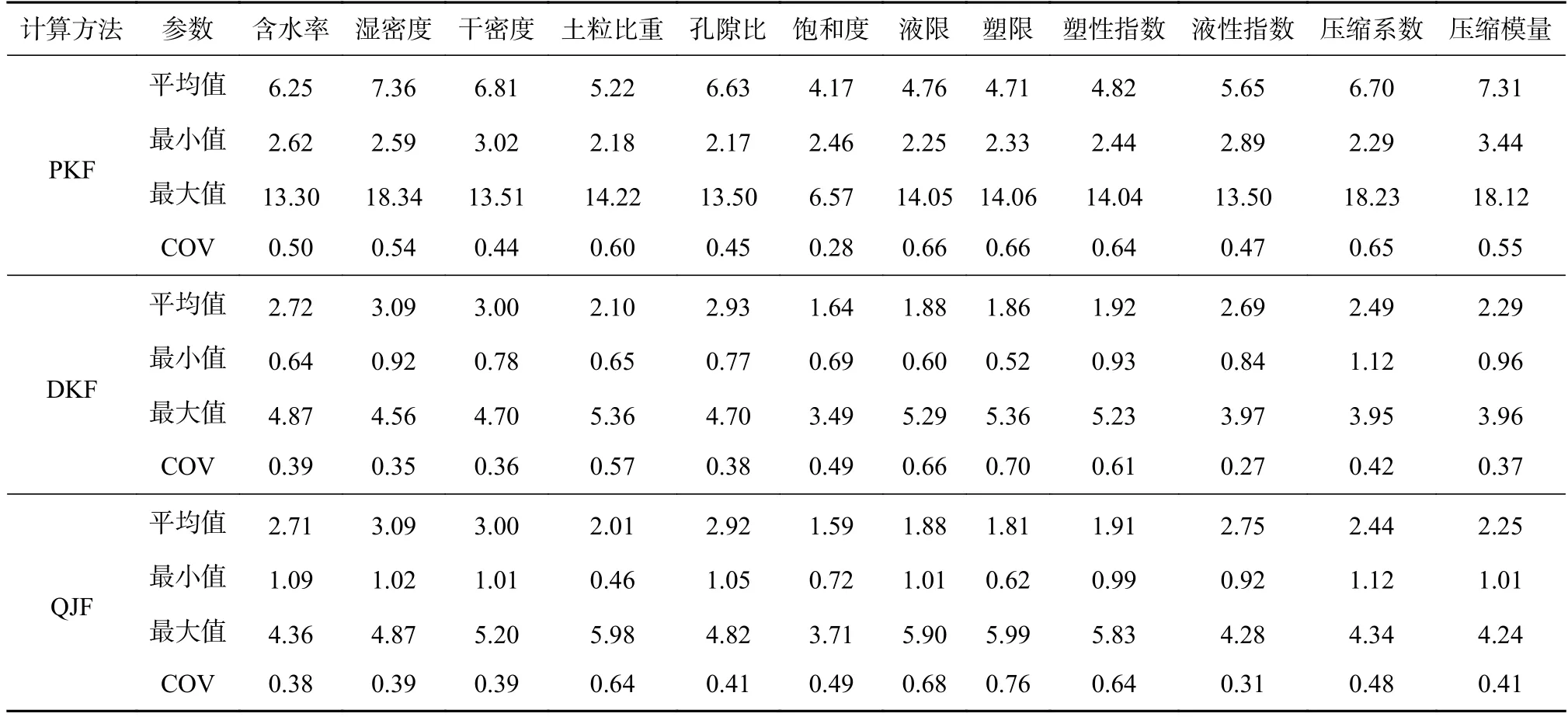
表3 土工参数的垂直自相关距离δv m

平均COV 是指12 个参数计算结果变异系数的平均值，3 种方法的平均COV 分别为0.54、0.46、0.50，其中递推空间法的COV 值最小，所以基于土工参数计算垂直自相关距离时，推荐采用递推空间法。

由递推空间法计算得到的土工参数δv的范围值为1.64～3.09 m，平均值为2.39 m，略大于静力触探数据的计算结果。静力触探为原位试验，在现场试验的过程中对土体的扰动小，而土工参数是现场取土后再到室内实验室进行的相关试验，必然会产生不同程度的扰动，最终造成计算结果偏大。与其他研究成果[17]对比发现，部分参数计算结果的范围值较为接近，但具体平均值有差距；而有些参数计算得出结果则差异较大，可能是由于土体本身各项参数指标存在差异造成的。

3 结论

（1）通过对比3 种方法计算土体自相关距离的结果发现，递推空间法的计算结果异常值少，且变异系数较小，不论采用静力触探数据还是土工参数时均推荐采用该方法计算土体的自相关距离。

（2）递推空间法计算结果显示，基于侧阻力fs、锥尖阻力qc和土工参数的土体垂直自相关距离平均值分别为2.28 m、1.84 m 和2.39 m；基于侧阻力fs、锥尖阻力qc的土体水平自相关距离平均值分别为18.24m 和19.21m。各参数得到的自相关距离较为接近，其中土工试验参数的计算结果略大于静力触探试验计算结果。

（3）本研究搜集和整理了较多的地质勘测资料，计算分析出研究区黏性土的自相关距离典型值，可用于分析岩土体参数的空间变异性，建立随机场模型，为考虑土体参数变异性的岩土工程设计及稳定性评价提供了研究基础。