基于无功源控制空间的自动电压控制系统聚类分区方法及关键节点选择

王馨悦 马星河

摘  要：自动电压控制（AVC）系统在降低电网损耗、维护电网稳定等方面发挥重要作用。在应用AVC系统时，需要对电网进行分区控制从而达到全局最优的控制目标。该文提出一种基于无功源控制空间的AVC系统聚类分区方法，在构建节点导纳矩阵、建立无功源控制空间的基础上，实现聚类分区。在完成分区后，选择中枢节点和临界节点作为子分区的关键节点。通过保证关键节点的电压水平稳定，实现输电网的可靠运行。

关键词：无功源控制；自动电压控制系统；导纳矩阵；电网；聚类分区

中图分类号：U665.12      文献标志码：A          文章编号：2095-2945（2024）06-0116-04

Abstract： Automatic voltage control （AVC） system plays an important role in reducing power grid loss and maintaining power grid stability. In the application of AVC system， it is necessary to control the power grid in different regions to achieve the global optimal control goal. In this paper， a cluster partitioning method for AVC system based on reactive power control space is proposed. On the basis of constructing node admittance matrix and reactive power control space， cluster partitioning is realized. After the partitioning is completed， we selected the hub node and the critical node as the key nodes of the sub-partition. By ensuring the voltage level of key nodes is stable， the reliable operation of transmission network is realized.

Keywords： reactive power source control; automatic voltage control system; admittance matrix; power grid; clustering partition

国内电力系统侧重于频率控制，关于电压控制的研究较少。近年来，大机组、超高压电网的应用越来越普遍，传统控制模式的弊端逐渐显现。相比之下，基于无功的自动电压控制在取得良好控制效果的基础上，还能兼顾电网运行的安全性和经济性，如何优化电力系统的自动电压控制成为热门研究课题。其中，聚类分区方法和关键节点选择是决定自动电压控制性能的2个关键因素，也是课题研究的重点。

1  基于无功源控制空间的聚类分区方法

1.1  基于等效处理的导纳矩阵构建

对于一些规模较大、覆盖范围较广的输电网，节点数量通常在几百甚至上千不等。为了降低研究难度，本文采取等效变换的方式构建输电网的等效节点导纳矩阵，具体包括2方面：其一是外部电网简化等效，其二是三绕组变压器等效。

1.1.1  外部电网简化等效

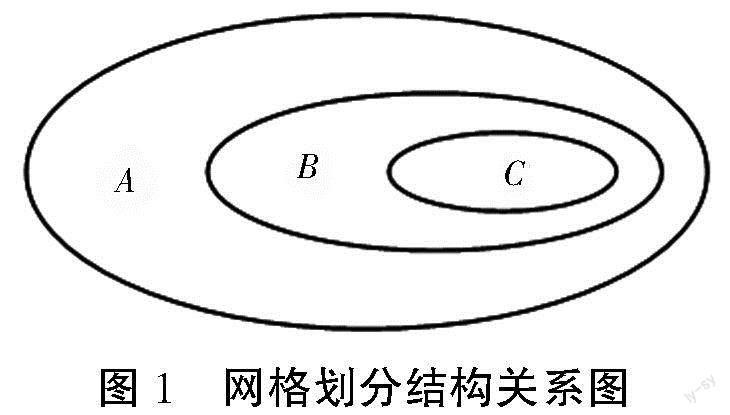
在输电网中，任意一个区域电网都不是孤立的，必然会与相邻的外部电网产生联系、相互影响，需要进行等效处理。将外部电网中所有的节点组成一个集合，用A表示；研究的区域电网与周边外部电网之间的边界节点组成一个集合，用B表示；在区域电网中，除了边界节点外的其他内部节点，用集合C表示。3个集合的关系如图1所示。

以分块矩阵形式来表示网络节点的电压方程，如下

式中：VA、VB、VC为不同节点的电压变量；IA、IB、IC为对应节点的电流变量。消去外部节点的电压变量VA后，上式可以转化为

上式即为等值后边界节点的导纳矩阵。

1.1.2  三绕组变压器等效

三绕组变压器是输电网中的一种重要设备，分别有高压、中压、低压3个绕组。向任意一个绕组通入交流电，在其他的2个绕组上会出现感应电势，并且按照设定比例升高或降低电压，达到变压效果[1]。电力系统中的三绕组变压器通常采用星形等效模型，如图2所示。

由图2可知，每台三绕组变压器中包含一个中心点O，从O点引出4条线路，1、2、3三条线路中每条线路都包含一个等效电阻和绕组；剩余一条线路经过接地电阻ym后接地。由于O点的存在，导致节点导纳矩阵的维数较高，相应的计算量也更大。本文在研究时将O点去除，得到低维等效节点导纳矩阵，这样一来三绕组变压器的等效模型也发生了变化，从星形变成了角形，如图3所示。

图3中，Y12、Y13、Y23均為等效电阻，表达式为

相应的，Y1m、Y2m、Y3m均为接地电阻，表达式为

利用以上公式对三绕组变压器进行等效处理后，不会对变压器的对外特性产生影响，这说明本文提出的消除中心点O的策略是可行的。除此之外，消除了中心点的三绕组变压器与电力系统中的其他设备（如电抗器、电容器等）结合，能够得到研究区域内所有节点，以及研究区域与相邻外部区域的边界节点组成的导纳矩阵，为开展无功源控制空间的聚类分区创造了便利条件。

1.2  无功源控制空间的建立

假设某个输电网的节点数量为N，在极坐标下该输电网中任意一个节点i（i=1，2，…，N）的注入平衡功率方程为

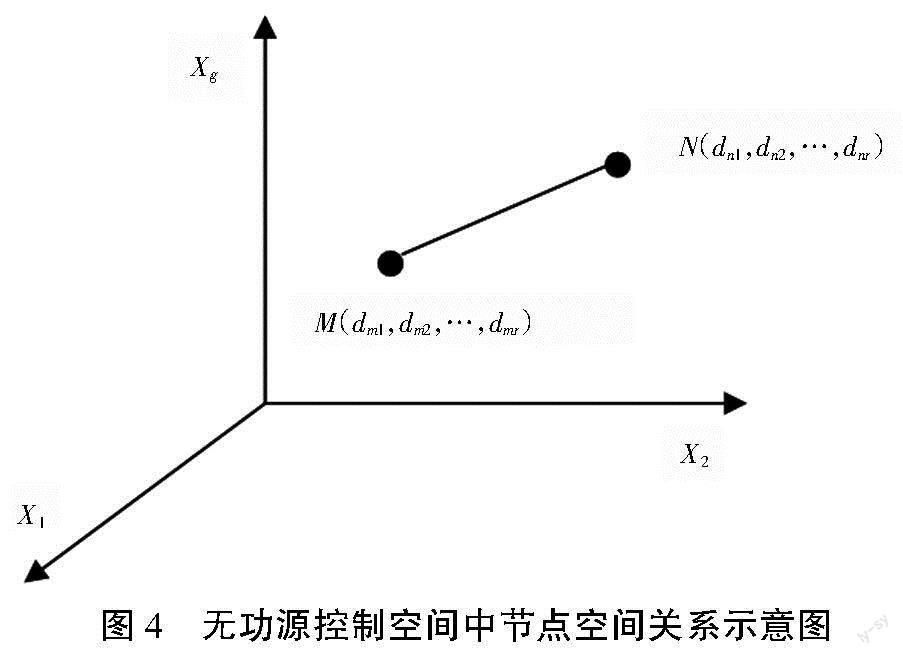
式中：Gij和Bij分别表示节点导纳矩阵中元素Yij的实部与虚部；Pi和Qi则表示第i个节点的注入有功和无功功率；Vi表示第i个节点的电压幅值；θi表示第i个节点的角度，θij=θi-θj。对于高压和特高压输电网中的自动电压控制系统，考虑到线缆的电抗远远超过电阻，并且线路两侧母线电压的相位差θij较小（通常不超过10°），因此电阻可以忽略不计，同时也意味着有功功率和无功功率的弱耦合联系可以忽略[2]。基于上述分析，假设输电网中任意2个节点之间的电气距离为d，根据d值的大小可以表示这2个节点之间无功电压联系的密切程度，如图4所示。

图4中，M和N表示输电网中任意的2个节点，两者之间的直线距离即为d。d值可以利用欧几里得公式求出，公式为

利用上述关系，可以建立无功源控制二维空间。假设某个研究区域内包含了r个无功源控制节点，这些节点组成一个集合，用{r}表示；该研究区域内包含t个被控节点，这些节点也组成一个集合，用{t}表示。使每个无功源控制节点的无功控制能力作为空间的一维，对于i∈{t}，可以用一组r维向量（di1，di2，…，dir）作为节点i在空间中的坐标。经过上述处理后，可以得到以等效电气距离为基础，以无功源为空间维度的“无功源控制空间”。该空间中，被控节点i的坐标向量可以反映出无功源控制节点对该节点控制的灵敏度[3]。

1.3  聚类分区方法的实现

聚类分区的原理是将任意一个被控节点都看作成一个独立的子分区，然后将若干个子分区进行合并，直到获得理想的分区结果，具体步骤如下。

步骤1：假设某个输电网中被控节点的数量为t，这些节点的集合为{t}。将该集合中包含的每一个节点作为一个子分区Oi（i=1，2，…，t）。经过分区后，该输电网被划分成t个子分区，即Ngroup=t。将被控节点在无功源控制空间中的距离Dij作为子分区Oi和Oj之间的距离。

步骤2：从t个子分区中，找出Om和On 两个子分区，保证两者之间的距离Dmn为任意2个不同子分区之间距离最小的一个。

步骤3：将子分区进行合并，经过i次合并后，得到Di=Dmn，合并之前的分区数Ni=Ngroup。在合并距离曲线上，第i次合并是对应点的坐标为（Di，Ni）。

步骤4：在子分区合并过程中，步骤2中找出的Om和On两个子分区被合并成了新的子分区Op，然后再次计算Op与其他新合并形成子分区Oq的距离。两者之间的距离可以表示为Dpq=min（Dmp，Dmq）。然后去掉Om和On，并且令Ngroup=Ngroup-1。

步骤5：执行一个判断程序“Ngroup=1？”如果判断结果为“是”，则继续进行下一步骤；如果判断结果为“否”，则返回步骤2。将各组（Di，Ni）坐标点串联起来，即可得到合并距离曲线，并根据曲线确定最终分区个数Nreal。

步骤6：当Ngroup=Nreal时，对应的分区结果即为被控节点最终的分区结果。最后按照“最小连通性”原则，将各无功源控制节点预期等效电气距离dij最小的被控节点所在的子分区合并，聚类分区结束[4]。整个过程如图5所示。

研究表明，在绘制合并距离曲线时，不可避免地会存在一个或多个明显拐点。这意味着合并距离曲线上存在一个特点的分区个数Nreal，如果“Ngroup>Nreal”，这种情况下曲线斜率偏大，合并的2个子分区的距离太小；反之，如果“Ngroup

2  自动电压控制系统子分区关键节点的选择

确定子分区的关键节点是聚类分析中的重要步骤，同时也直接决定了聚类分区结果的质量。本文分别选取了子分区中的中枢节点和临界节点作为关键节点，并对每一种节点的选择方式展开了分析。

2.1  子分区中枢节点排序

在子分区中，中枢节点的电压值实际上代表了该子分区内所有节点的平均电压水平。在选择中枢节点时，除了要考虑电压的高低外，还要判断该节点的电压是否可调。因此，确定子分区中枢节点时应满足以下2项条件：其一，必须为无功源控制节点，保证电压可调；其二，对子分区内其他被控节点的电压具有较好的灵敏度，即中枢节点可以控制子分区其他被控节点的电压[5]。已知等效电气距离能够表示子分区中任意2个节点之间的电压关系，假设某个子分区中无功控制节点的集合为{W}，被控节点的集合为{M}，对于所有i∈W，可以得到

式中：Dsumi表示研究区域内第i个无功控制节点与其他被控节点的等效电气距离之和。如果该值较小，则说明这个无功控制节点对整个子分区节点电压的灵敏度较高，控制效果较好。分别求得研究区域内全部分区的Dsumi值，然后将其按照从小到大的顺序进行排列。根据其中的最小值，即可选出子分区的中枢节点。

2.2  子分区临界节点的选择

子分区中某些被控节点对于轻微的电压变化也会表现的十分敏感，这些节点被称为临界节点。输电网正常运行时，在中枢节点的调控下，临界节点的电压始终维持在略高于临界值的状态；如果输电网发生短路等故障，必须要采取紧急控制措施，这时需要将临界节点快速切除，避免對输电网造成更大的破坏。假设i和j是某个子分区中的2个节点，当节点j发生电压波动后，会对节点i产生影响，该影响用Hij表示。则被控节点的电压灵敏度可表示为

式中：Ui表示节点i对电压变化的灵敏度，该值越大说明灵敏度越高；Oall表示该子分区中所有节点的集合。按照上述方法分别计算出子分区中所有节点电压变化对于i节点的影响，并将计算出来的Ui值进行排序，其中最大的Ui值对应的节点，即为子分区的临界节点。有时候多个Ui值的差距不明显，则可以选择较大的几个Ui值对应的多个被控节点作为临界节点。

3  结束语

在电网结构复杂、电压等级升高、电网负荷加重的背景下，如何保证电网的稳定运行成为电力公司和电力用户共同关注的焦点，本文提出的一种基于无功源控制空间的自动电压控制系统，首先对输电网进行聚类分区，然后让自动装置按照指令实现闭环控制，通过分区最优达到全局优化的控制目标，使得电网得到稳定和经济运行。

参考文献：

[1] 支晓晨，李玉齐，高熹，等.基于抽蓄电站自动电压控制系统的改进无功分配策略研究与应用[J].电气技术，2023（4）：74-80.

[2] 黄际元，黄珂琪，杨俊，等.储能参与电网调压与动态无功支撑的协调控制策略[J].电器与能效管理技术，2020（10）：8-12.

[3] 唐晓骏，罗红梅，陈萌，等.计及柔性直流的城市电网多源无功控制及短路电流修正策略[J].全球能源互联网，2021（4）：104-105.

[4] 李克明.基于DTW距离和聚类分析的配电台区低压拓扑结构辨识方法[J].电力系统保护与控制，2021（14）：82-85.

[5] 王常安，刘俊勇.提高VSC无功功率支撑能力的直流电压补偿控制策略[J].电力系统及其自动化学报，2023（2）：63-74.