纯剪状态下蜂窝梁腹板的弹性屈曲分析

范财军 邓皓 熊竹筠 田如萍 袁辉 刘兴

摘  要：该文利用有限元软件建立正六边形孔蜂窝梁腹板在纯剪应力状态下的有限元模型，研究四边简支开孔板在纯剪状态下的屈曲模式，分析孔洞尺寸对蜂窝梁腹板屈曲临界应力的影响，提出纯剪状态下开孔板的屈曲系数计算公式，得到蜂窝梁开孔腹板在纯剪状态下的高厚比限值。研究表明，单孔板和双孔板的最大屈曲平面外位移处的连线均与水平方向呈45°，四孔板和六孔板则有2种屈曲模式；蜂窝梁腹板孔高比和距高比是影响开孔板屈曲临界应力的主要因素，建议对于剪力作用较大的蜂窝梁腹板取孔高比γ<0.5，距高比0.4<β<0.5的孔洞尺寸，使得容易实现稳定性和经济性要求；拟合的开孔板屈曲系数公式误差不超过5%，具有良好的精度。

关键词：蜂窝梁；开孔板；纯剪切；弹性屈曲；有限元模型

中图分类号：TU313.1      文献标志码：A          文章编号：2095-2945（2024）06-0012-06

Abstract： In this paper， the finite element model of the web of regular hexagonal perforated honeycomb beam under pure shear stress is established by using finite element software， and the buckling mode of quadrilateral simply supported perforated plate in pure shear state is studied. The influence of hole size on the buckling critical stress of honeycomb beam web is analyzed， the buckling coefficient formula of perforated plate in pure shear state is put forward， and the limit value of height-thickness ratio of perforated web in pure shear state is obtained. The results show that the connection line at the maximum buckling plane displacement of single-hole plate and double-hole plate is 45° to the horizontal direction， while four-hole plate and six-hole plate have two buckling modes， and the hole height ratio and distance height ratio of honeycomb beam web are the main factors affecting the critical buckling stress of perforated plate. It is suggest taking the hole height ratio for honeycomb beam web plates with high shear force γ<0.5， hole size with a distance to height ratio of 0.4<β<0.5， making it easy to achieve stability and economic requirements. The error of the buckling coefficient formula of the fitted perforated plate is less than 5%， with a satisfactory accuracy.

Keywords： honeycomb beam; perforated plate; pure shear; elastic buckling; finite element model

蜂窩梁研究与应用成果已广泛应用于实际工程。与相同用钢量的实腹式梁相比，其具有抗弯刚度大的优点。但其腹板的连续性因为开孔而被打断，使得蜂窝梁的腹板屈曲成为蜂窝梁失效的关键研究内容。

目前，蜂窝梁的研究由于开孔形式差异，理论推导复杂，没有相应的理论解。相关的研究主要有Hagen等进行了大量的实验和有限元模拟来确定开孔腹板梁的受剪极限承载力，提出了适合梁腹板开孔时受剪承载力的计算公式[1-4]。Redwood等提出了蜂窝梁腹板屈曲系数计算方法[5-6]。本文参考了梁嘉[6]的研究方法，把蜂窝梁腹板单独分离出来做为开孔薄板进行纯剪研究。但在蜂窝梁中翼缘和腹板的协同工作不可忽略，吴丹丹[7]在对腹板开圆孔H型钢梁纯剪抗力研究时引入了纯剪抗力影响系数以考虑梁翼缘对抗剪的贡献。贾连光等[8]通过试验研究提出了蜂窝组合梁的等效抗剪刚度计算公式。刘子楠[9]对蜂窝梁进行实验及数值模拟，得出蜂窝梁典型截面的应力与挠度受跨高比和孔高比的影响较大，受长高比和距高比的影响较小。故结合开孔腹板纯剪状态下在蜂窝梁受剪屈曲分析时以孔高比、距高比作为主要参数。

本文借鉴实腹式工字梁的弹性屈曲稳定研究方法，对蜂窝梁腹板在纯剪应力下的弹性屈曲应力进行了分析。通过特征值屈曲分析，研究了纯剪蜂窝梁的屈曲模式和特征值，并进一步考虑翼缘对于腹板的约束作用，得出蜂窝梁腹板的高厚比限值。

1  有限元模型的建立与验证

1.1  有限元模型的建立

有限元模型为四边简支的开孔板，利用shell181单元，网格划分尺寸为10 mm。板的四边简支约束，限制住开孔板各边的节点的平面外位移。同时，为了方便有限元模型发生刚体移动，采用约束一个角端的横向和竖向线位移以及其对角端的竖向线位移。荷载施加在板的边界上，参考剪力互等定理，纯剪受力状态下的矩形板，相邻剪力大小相等，符号相反。荷载施加时，采用在有限元模型四边的中间节点施加单位荷载1，4个端点施加荷载0.5的方式[10]。开孔腹板纯剪受力状态加载示意图如图1所示，对应的有限元模型如图2所示。

1.2  有限元模型的验证

有限元模型的验证采用实腹式四边简支板在纯剪状态下进行特征值分析[11]。模型仅取板的长度L为变量，其他量为常值。按厚度t=4 mm，高度H=600 mm，μ=0.3，E=2.06×105 N/mm2，表1为有限元数值解和理论解[12]的对比。

由表1可知，有限元数值解与理论解误差很小，说明采用此种有限元模型进行分析模型的弹性屈曲是可行的。

2  纯剪状态下开孔腹板的屈曲模式

建立的开孔腹板的有限元模型包括单孔板、双孔板、四孔和六孔板，并研究四边简支六边形开孔腹板在纯剪受力状态下的弹性屈曲。

2.1  单孔板

单孔板在承受均匀受剪时，其屈曲模式表现为正六边形孔的相对斜角处出现最大平面外位移，两处最大位移之间的连线与水平长度方向成45°，且屈曲位移指向同侧，如图3所示。其原因主要是板沿着主拉应力方向会产生较大屈曲，屈曲方向与主压应力垂直且与水平线成45°，板中虽存在孔洞，但未影响整个板的应力分布。故最大屈曲位移出现在45°方向开孔边缘较薄弱位置处。

2.2  双孔板

双孔板在承受均匀受剪时，其屈曲模式表现为板的最大平面外位移出现在靠近中间腹板的斜角处的2个开孔边缘，两处最大位移间的连线仍与水平轴成45°，中间板并未产生平面外位移，两孔边缘处的平面外位移指向异侧，如图4所示。其原因主要是沿着主拉应力方向会产生较大屈曲，但因孔间板具有较大的刚度，虽不影响板的屈曲方向，即屈曲方向与水平線仍近似成45°，但两孔洞平面外位移方向相反的稳定状态更容易实现。

2.3  四孔、六孔板

四孔板和六孔板的屈曲模式有2种，其原因主要是整个板的屈曲方向虽沿着主拉应力方向分布，但由于孔间板的约束，孔洞屈曲会随机地按照更容易实现再平衡状态的方式进行。第一种屈曲模式为孔洞周围发生屈曲，孔间未发生屈曲，相邻两孔间平面外位移方向指向相反，如图5所示。

另一种屈曲模式为靠近跨中开孔板中心的两孔洞周围平面外位移与孔间板平面外位移方向相同，接近中间两孔的其他孔洞平面外位移向异侧屈曲，如图6所示。

3  纯剪状态下孔洞尺寸对屈曲临界应力的影响

孔间距离和孔洞高度是影响蜂窝梁屈曲承载能力的主要参数。文献[6]表明，开孔板发生弹性屈曲时孔洞数对承载力影响很小。选取单孔板和双孔板为对象，研究孔洞尺寸对板屈曲承载力的影响。通过距高比（β=s/H）和孔高比（γ=h/H）双变量研究开孔板剪切屈曲性能，其具体控制参数参考了美国的《Specification for Structural Steel Beams with Web Openings》[13]。具体的孔高比取值范围为0.3≤γ≤0.7，距高比取值范围为0.4≤β≤1.1，分析了共计320个模型。

通过对板厚分别为4、6 mm的单孔板和双孔板进行特征值屈曲分析，其对应的高厚比分别为100和150，得到不同孔高比和距高比下的屈曲临界应力。

3.1  孔高比γ对屈曲临界应力的影响

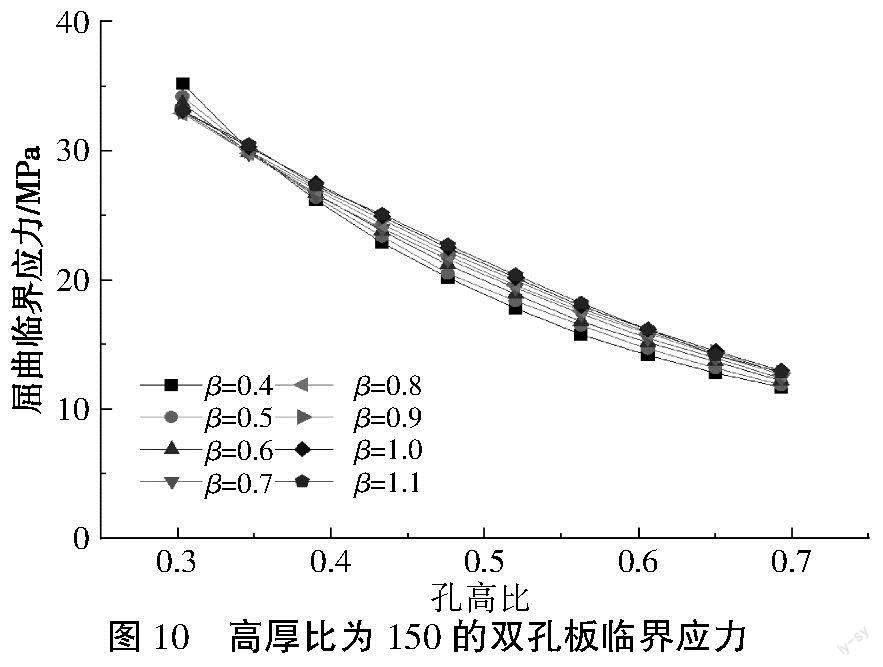
以孔高比为横坐标，屈曲临界应力为纵坐标表示出了高厚比分别为100、150的单孔板和双孔板屈曲临界应力的变化规律，如图7—图10所示。

由图7—图10可知，纯剪状态下，腹板高厚比是影响开孔板屈曲临界应力的重要因素。在相同几何参数的情形下，高厚比为100的开孔板的临界应力约为高厚比为150的开孔板的2倍；随着板孔高比增加，板屈曲临界应力均有大幅度降低，主要是由于孔洞周围的板能提供的约束作用有限，孔洞尺寸增加所导致的临界应力的降低程度大。

3.2  距高比β对屈曲临界应力的影响

以距高比为横坐标，屈曲临界应力为纵坐标表示出了高厚比分别为100、150的单孔板和双孔板屈曲临界应力的变化规律如图11—图14所示。

由图11—图14可知，对单孔板，当γ<0.6时，随着距高比增加，临界应力有所降低，是由于薄板的尺寸起主要作用，尺寸增大则更容易发生屈曲；当γ≥0.6时，随着距高比的增加，临界应力处于相对稳定状态，因为间距增加和尺寸增大的作用效应基本持平；而双孔板随着距高比的增加，各种孔高比状态下的屈曲临界应力变化很小。进一步分析，由于板平面尺寸对纯剪状态下的屈曲影响较大，可以得出当开孔板尺寸越大，越容易发生屈曲，故双孔板的临界应力比单孔板的临界应力低。

4  纯剪状态下开孔腹板的屈曲系数

4.1  实腹式四边简支板的弹性屈曲系数

实腹式四边简支板在承受均匀剪力作用下，其屈曲荷载可利用四边简支的正方形板承受均匀剪力来求解。采用迦辽金法来计算时，板的中面力Nxy=Nyx=Pxy=Pyx，而Nx=Ny=0，板的平衡偏微分方程为

矩形板分析可得到

Pcrxy=ksπ2D/b2，（2）

式中：ks为剪切屈曲系数，对于四边简支板

当L≥H时，

ks=5.34+4.0（H/L）2 ； （3）

当L

ks=4.0+5.34（H/L）2 。 （4）

4.2  纯剪状态下开孔腹板的屈曲系数

本文采用等效刚度法进行弹性屈曲系数公式的分析。将纯剪状态下开孔板的屈曲系数设为k′s，利用有限元软件分析得到的临界荷载反算出开孔板的屈曲系数k′s，将实腹板的剪切屈曲系数ks作为基础，对数据进行回归分析，则可得到考虑孔高比和距高比的剪切屈曲系数公式。并利用数值分析软件MATLAB拟合出的开孔板剪切屈曲系数公式为

单孔板

双孔板

式中：ks为相应实腹板的剪切屈曲系数。

式中：L为板单元长；H为板单元高；β为距高比，β=s/H，适用范围为0.3≤β≤1.1；γ为孔高比，γ=h/H=D/2H，适用范围为0.3≤γ≤1.1；D为边形孔的外接圆直径。

表2和表3是根据公式（5）和（6）计算得到的剪切屈曲系数，对比有限元解可以发现，回归分析得到的剪切屈曲系数公式具有良好的精度，误差小于5%。

5  翼缘对腹板的约束作用

以上均是假定腹板受到翼缘的约束为简支条件下对开孔腹板的弹性屈曲分析。然而，翼缘对腹板的约束作用并非简单的简支条件，而是不同程度嵌固作用。实际的翼缘弹性嵌固作用会使临界应力相应地提高[14]，蜂窝梁腹板的嵌固系數与腹板高厚比，翼缘宽厚比，翼缘与腹板厚度比有关。任涛等[15]利用实腹梁验证了ε=bf tf3/hw tw3是一个能够较准确表达翼缘对腹板约束作用的参数。

GB 50017—2017《钢结构设计标准》采用嵌固系数来表达实腹式腹板受剪应力屈曲时翼缘对腹板的约束作用。对于受剪应力屈曲的腹板，取约束系数为χ=1.23。蜂窝梁在腹板上存在着孔洞，其腹板受到翼缘的约束作用更大，本文借鉴实腹梁的相关规定，偏于保守的取约束系数为χ=1.23。

参考实腹梁腹板在剪应力单独作用下不发生失稳的临界应力条件，对于剪应力屈曲的开孔腹板应满足

取弹性模量E=2.06×105 N/mm2，泊松比μ=0.3，则开孔腹板在剪应力屈曲时的腹板高厚比限值

6  结论

本文对六边形孔蜂窝梁腹板进行了纯剪受力状态下的弹性屈曲分析，研究了其屈曲模式和屈曲应力的变化规律，利用数值分析软件MATLAB拟合了相关剪切屈曲系数公式，得到如下结论。

1）纯剪状态下四边简支单孔板，双孔板，最大位移之间的连线与水平长度方向成45°。四孔板与六孔板的屈曲模式主要分为2种：一种是孔洞跨中周围发生屈曲，孔洞之间板未发生屈曲，相邻两孔洞平面外屈曲方向相反；另一种是腹板靠近跨中的两孔洞周围与孔洞之间腹板指向同一平面外方向发生屈曲，而靠近中间两孔的平面外位移方向指向异侧。

2）蜂窝梁腹板的屈曲临界应力随孔高比的增加而大幅度降低，随距高比的增加则几乎保持不变。建议以受剪屈曲为主的开孔板取γ<0.5，0.4<β<0.5， 能同时满足较高稳定性和经济性要求。

3）开孔腹板在剪应力屈曲时的腹板高厚比限值应满足

参考文献：

[1] HAGEN N， LARSEN P. Shear capacity of steel plate girders with large web openings[J]. Part II： Design guidelines. Journal of Constructional Steel Research， 2009，65（1）：151-158.

[2] ERDAL F， SAKA M P.  Ultimate load carrying capacity of optimally designed steel cellular beams[J]. Journal of Construction Steel Research， 2013，80（1）：355-368.

[3] 杜嘉慧，毕然，贾连光.正六边形蜂窝梁应力计算方法研究[A].中国钢结构协会结构稳定与疲劳分会.中国钢结构协会结构稳定与疲劳分会第17届（ISSF-2021）学术交流会暨教学研讨会论文集[C].中国钢结构协会结构稳定与疲劳分会：工业建筑杂志社2021：5.

[4] 梁梦蝶.拼接板连接蜂窝梁抗剪性能研究[D].济南：山东大学，2020.

[5] REDWOOD R G， DEMIRDJIAN S. Castellated beam web buckling in shear[J]. Journal of Structural Engineering. American Society of Civil Engineers，1998，124（8）：1202-1207.

[6] 梁嘉.纯剪状态下蜂窝梁腹板的局部稳定性分析[D].长沙：湖南大学，2013：46-71.

[7] 吴丹丹.腹板开圆孔H型钢梁力学性能研究[D].西安：西安建筑科技大学，2019.

[8] 贾连光，李鹏宇，焦禹铭.六边形孔蜂窝组合梁的等效抗剪刚度研究[J].沈阳建筑大学学报（自然科学版），2020，36（1）：11-18.

[9] 刘子楠.矩形孔蜂窝梁构件力学性能研究[D].大连：大连理工大学，2021.

[10] 吴家龙.弹性力学[M].上海：上海同济大学出版社，1987.

[11] 张益凡.蜂窝梁的整体和局部稳定分析[D].长沙：中南大学，2008：7.

[12] 陈骥.钢结构稳定理论与设计[M].6版.北京：科学出版社，2014.

[13] Specification for Structural Steel Beams with Web Openings： ASCE 23-97[S].Virginia： American Society of Civil Engineers，1998.

[14] 夏志斌，姚谏.钢结构[M].杭州：浙江大学出版社，2004.

[15] 任涛，蔡渊，童根树.工字梁腹板的剪切屈曲系数分析[C]//第四届海峡两岸结构与岩土工程学术会议论文集，2007：543-550.